Rep:Module1:mr60712789
Computational Chemistry Lab- Module 1: Organic
Molecular Mechanics (MM) can be used to provide specific information about a molecule. The process works by creating an optimum steric energy value by taking into account 5 main factors: The bond stretching term, the bond angle, the torsion of a bond given by its dihedral term, a term for hydrogen bonding, and a non-bonded term comprising of the Leonard-Jones Potential and an electrostatic term. In the following examples of cyclopentadiene dimers, the nucleophilic additions to pyridinium rings and the synthesis of Taxl, the molecular mechanics method used is MM2 . Despite MM2 being able to process the data for large molecules and producing accurate values for such systems, the method of analysis fails for more complex molecules containing metal atoms. Furthermore the method works by assuming that no bonds are broken, which is not the case for most reactions, thus making the method insufficient for analysis of transition states.
Cyclopentadiene Dimer
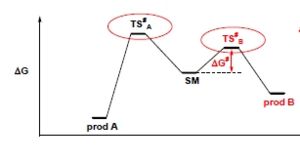
Cyclopentadiene dimerisation and hydrogenation is controlled either thermodynamically or kinetically. Thermodynamic control occurs when the reaction pathway taken eventually leads to the formation of the more stable product. This pathway may travel through more than 1 other product (or intermediate) which is higher in energy, and this product is known as the kinetic product. This product is formed when the reaction pathway followed has the smaller activation energy barrier.
This is shown in the following diagram where the starting material (sm) is able to pass over the smaller energy barrier, through transition state B through to the higher energy product B. However this is reversible product B is also able to travel back to the starting material and then back over the larger activation energy barrier to the lower energy porduct A. Product B is therefore the kinetic product because it is able to return and be changed into product A, but due to the size of the activation barrier product A is unable to return to the starting material, thus making it the thermodynaic product.
Dimerisation of Cyclopentadiene
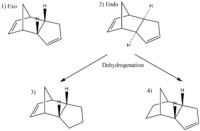
Cyclopentadiene dimerises stereospefically to form the endo dimer. Both the endo (molecule 2) and exo (molecule 3) dimers were optimised using ChemBio3D and the Molecular Mechanics 2 option, yielding the following results:
| Type of Energy | Exo Dimer | Endo Dimer | ||
| Energy/kcalmol-1 | Energy/kJmol-1 | Energy/kcalmol-1 | Energy/kJmol-1 | |
| Stretch | 1.283 | 5.3 | 1.260 | 5.2702 |
| Bend | 20.588 | 83.1 | 20.840 | 87.1950 |
| Stretch-Bend | -0.837 | -3.5003 | -0.838 | -3.5045 |
| Torsion | 7.640 | 31.9637 | 9.509 | 39.7869 |
| Non-1,4-VdW | -1.400 | -5.8559 | -1.530 | -6.4015 |
| 1,4-VdW | 4.232 | 17.7067 | 4.313 | 18.0473 |
| Dipole/Dipole | 0.377 | 1.5782 | 0.447 | 1.8682 |
| Total Energy | 31.883 | 133.3981 | 34.001 | 142.2614 |
Although the endo product has the highest energy it is also the major product, meaning that the endo product is the kinetic product and that the reaction is kinetically controlled. This means that the reaction involves the kinetically controlled endo transition state being lower in energy than that of the exo transition state. If the exo transition state was lower in energy then the endo product would not form as both the exo transition state and product would be lower in energy. The exo product contains the majority of the energy of the molecule within the bend component. This means that there is a large deviation from the optimum bond angles within the molecule. This deviation from the desired molecular bond angles is due to the steric hinderance and Van der Waals forces experienced by the molecule. Similarly the endo product also contains the majority of the molecule's energy within bend, although the endo product has a larger anount of energy within the bend than the exo. This is due to a larger steric interaction and greater Van der Waals forces being experienced by the endo molecule.
Hydrogenation of Cyclopentadiene
Similar to the dimerisation of cyclopentadiene, the hydrogenation of the dimerisation product can be thermodynamically or kinetically controlled.
| Type of Energy | Molecule 3 | Molecule 4 | ||
| Energy/kcalmol-1 | Energy/kJmol-1 | Energy/kcalmol-1 | Energy/kJmol-1 | |
| Stretch | 1.266 | 5.2965 | 1.104 | 4.6191 |
| Bend | 19.806 | 82.8696 | 14.540 | 60.8333 |
| Stretch-Bend | -0.828 | -3.4627 | -0.550 | -2.3000 |
| Torsion | 10.870 | 45.4792 | 12.505 | 52.3213 |
| Non-1,4-VdW | -1.221 | -5.1074 | -1.076 | -4.5003 |
| 1,4-VdW | 5.639 | 23.5953 | 4.495 | 18.8088 |
| Dipole/Dipole | 0.162 | 0.6782 | 0.141 | 0.5887 |
| Total Energy | 35.695 | 149.3491 | 31.159 | 130.3709 |
Similar to the dimers, both the molecules contain the majority of their energy within bend, with molecule 4 having a significantly lower amount of energy in the bend than molecule 3. Contribution wise both molecules have a similar contribution from stretch, torsion and dipole/dipole, however molecule 3 has a larger contribution from 1,4- Van der Waals and stretch-bend, and both 3 and 4 have similar hydrogen bonding (non-1,4-Van der Waals). Overall the energies decreased from having bending as the largest contribution, followed by torsion, 1,4-Van der Waals, hydrogen bonding, stretch-bend and with the smallest contribution from the dipole/dipole.
Molecule 4 is the thermodynamic product as it has the lowest overall energy and moleucle 3 is the kinetical product becuase it is higher in energy. Thus molecule 4 is the major product and therefore the hydrogenation of the endo dimer is thermodynamically controlled. The lower energy of molecule 4 can be rationalised in 2 ways:
–Firstly: The stretch energy of molecule 4 is lower than that of molecule 3 meaning less deviations in molecule 4 from the ideal bond length. Furthermore there is only a small contribution from intermolecular 1,4-Van der Waals forces meaning that there are fewer steric inteactions and so the molecule is lower in energy.
–Secondly: The ring strain of molecule 4 is lower than that of molecule 3, shown in the bend contribution to total energy. Molecule 4 has a lower bend energy meaning that the molecule contains fewer deviations from the desired bond angles. Molecule 3 has the double bond present in the six membered ring and molecule 4 has the double bond present in the five membered ring. Sp2 double bonds have an ideal bond angle of 120˚, however in molecule 3 the bond angle is 107.8˚ and in molecule 4 the bond angle is 112.4˚. Therefore molecule 4 has a smaller difference between optimal and actual bond angles, therefore the energy of molecule 4 is lower.
It must be noted that it is possible to rationalise the production of the endo product with respect to the endo rule: "The most stable transition state results when there is a maximum accumulation of double bonds. It most often applies when dealing with cylic dienes and dienophiles. [1] . Assuming that the HOMO of one cyclopentadiene is the diene and the LUMO of cyclopentadiene is the dieneophile, then there will be 2 new sigma bonds formed as well as 2 non bonding interactions. [2]. Thus the presence of the non-bonding interactions between 2 cyclopentadiene molecules will stabilise the transition state leading to the endo product. Therefore the higher energy endo product may still be produced and could potentially be the major product instead of the lower energy product.
Stereochemistry of Nucleophilic Additions to a Pyridinium Ring (NAD+ Analogue)
The following 2 molecules show 2 different nucleophilic addition reactions: one in which an optically active deivative of prolinol is reactied with a magnesium Grignard reagent which alkylates the pyridinium ring at position 4, and the second in which a pyridinium ring is reacted with analine transfering a NHPhenyl group onto the ring.
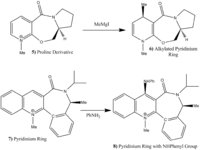
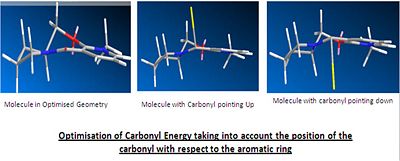
The reaction of molecule 5 with the grignard reacts stereospecifically to produce product molecule 6 exclusively. An attempt to model the attack of the Grignard was made, however ChemBio3D does not contain the element Magnesium and so the software will not support the reaction. The stereospecificity of the reaction to produce only product 6 is due to the attack of the Grignard reagent. As explained below, the carbonyl group lies 8˚ above the ring. The magnesium of the Grignard coordinates to the carbonyl oxygen during the reaction to form a 6 membered transition state. This will mean that as the carbonyl is above the plane then the magnesium will coordinate slightly above the plane and therefore the delivery of the methyl group will be above the plane. This leads to the observed stereochemistry of the product.
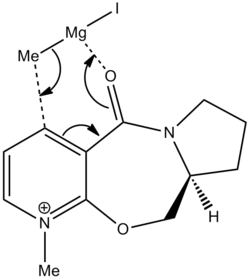
Grignard Reaction with Proline Derivative
The majority of the energy is split between bend and 1,4-Van der Waals, also with quite a large contribution from the charge/dipole. This shows that there are large deviances from the desired bond lengths and intermolecular forces within the molecule. The geometry of the carbonyl with respect to the aromaitc ring was investigated, yielding the following results.
 The energy of molecule 5 was optimised yielding the a total energy of 43.128 kcal/mol. The majority of the energy is split between bend and 1,4-Van der Waals and also quite a large contribution from the charge/dipole. This shows that there are large deviations from the desired bond lengths and intermolecular forces within the molecule. The geometry of the carbonyl with respect to the aromaitc ring was investigated, yielding the results to the left.Both the optimisations of the carbonyl pointing up and the carbonyl pointing down led to the carbonyl being in the planar position as shown in the original optimisation. This optimum angle was found to be 8˚.
 By optimising the energies in both the positions where either the oxygen is up and the methyl is down or when the methyl is up and the oxygen is down, the energy returned to the optimum value obtained by previous minimisation in which the methyl and oxygen are alomost planar with the methyl only slightly below the plane and the oxygen slightly above the plane. The energy of the grignard reaction product, the alkylated proline ring, was minimised and the energy was found to be at a value of 36.510kcalmol-1, lower than that of the non-alkylated product.  It is also important to note that large distortions to the carbonyl and aromatic ringsm molecule 5 will lead to molecules with high energies such as 378.8332kcal/mol |
Reaction of Pyridinium Ring with Analine
| Type of Energy | Molecule 7 | |
| Energy/kcalmol-1 | Energy/Jmol-1 | |
| Stretch | 4.016 | 16804.618 |
| Bend | 11.791 | 49333.126 |
| Stretch-Bend | 0.411 | 1717.532 |
| Torsion | 9.565 | 40019.542 |
| Non-1,4-VdW | 4.202 | 17582.005 |
| 1,4-VdW | 29.297 | 122576.556 |
| Charge/Dipole | 9.030 | 37779.846 |
| Dipole/Dipole | -4.881 | -20421.267 |
| Total Energy | 63.430 | 265391.957 |
Molecule 7, a pyridinium ring, reacts with analine to give a NHPhenyl secondary amine substitued product. The energy of the optimised molecule was found to be 63.4302 kcal/mol. The optimised molecule produced an angle of the carbonyl above the aromatic ring of 20˚. The analgous reaction of the analine with the pyridinium ring will follow the opposite stereochemistry as the reaction to form molecule 6 due to the carbonyl lying above the plane. The nucleophilic lone pair on the nitrogen will attack the ring from the opposite stereochemistry of the carbonyl group, i.e. as the carbonyl group lies above the plane of the molecule by 20˚ then the attack of the nucleophile will be from below the plane of the molecule. The NHPhenyl group has the same stereochemistry of the methyl attached to the seven membered ring. This is because the methyl group has opposite stereochemistry to the carbonyl, as seen in the model below. The nitrogen lone pair attacks in the same plane as the methyl group (opposite to that of the carbonyl) to give the same stereochemistry of the NHPh and the Me groups. The energy of the product molecule 8 was minimised and the energy found to be 58.825kcal/mol, and is where the methyl and iPr substituents are placed as far away from the bulky substituents in the starting material.
The MM2 model may be improved because the model does not take into account bond breaking and bond forming, which is clearly present in the mechanisms for the alkylation and the reaction with analine. To overcome this a different method of analysis could be applied, for example Gaussian could be used to minimise the energy, or the MOPAC programme.
Key literature
- Shultz, A.G; Flood, L.;Springer J. P.; J. Org. Chemistry, 1986, 51, 838. DOI:10.1021/jo00356a016
- Leleu, S; Papamicael, C; Marsais, F; Dupas, G; Levacher, V. Tetrahedron: Asymmetry, 2004, 15, 3919-3928. DOI:10.1016/j.tetasy.2004.11.004
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
Both molecules 9 and 10 were proposed as key intermediates in the synthesis of taxol by Paquette. The difference in the 2 molecules is the position of the carbonyl, an example of atropisomerism: where different stereoisomers can be isolated as confomers due to hindered rotation about bonds and where steric strain is a barrier to rotation. Molecule 9 (found later to be the twist-boat conformer) and molcule 10( found later to be in the chair conformer) isomerise further to an alternative carbonyl position. Both molecules were drawn in ChemDraw and the energies minimised using the MM2 method. By minimising their energies the energies obtained for both molecules was the same. This is because the downward carbonyl isomer (10) automatically moved the carbonyl group to face upwards (molecule 9). To overcome this problem the carbonyl was manually moved downwards and the carbons of the cyclohexane ring were altered to orientate themselves so that the carbonyl did not automatically move.
| Type of Energy | Molecule 9 | Molecule 10 | ||
| Energy/kcalmol-1 | Energy/kJmol-1 | Energy/kcalmol-1 | Energy/kJmol-1 | |
| Stretch | 2.659 | 11.123 | 4.746 | 19.856 |
| Bend | 11.180 | 46.776 | 76.486 | 320.018 |
| Stretch-Bend | 0.379 | 1.587 | 0.076 | 0.318 |
| Torsion | 22.938 | 95.973 | 19.888 | 83.213 |
| Non-1,4 VdW | -1.038 | -4.345 | 0.008 | 0.035 |
| 1,4-VdW | 13.994 | 58.550 | 25.034 | 104.740 |
| Dipole/Dipole | -0.175 | -0.731 | -0.083 | -0.348 |
| Total Energy | 49.937 | 208.935 | 126.155 | 527.831 |
 |
 |
|
|
|
These molecules yielded the results shown in the table. Due to the high total energy value of molecule 10 the moelcule was reoptimised to see whether a lower energy could be obtained.
The energy for this molecule was minimised by moving the almost planar carbonyl below the plane of the molecule. This yielded a total energy of 61.1215kcal.
An attempt was made to reminimise this and the Energy was found to be 44.3247kcal/mol.
Upon first minimisation the results showed that molecule 9 was much lower in energy than molecule 10. Upon further investigation this high value of energy for molecule 10 was found to be a local minimum and molecule 10 eventually was found to be lower in energy than molecule 9. These results suggest that molecule 10, in which the carbonyl group is pointing down is the most thermodynamically stable. Molecule 9 has a conformation in which the carbonyl is up and the cyclohexane ring adopts the twist-boat conformation which, whilst still containing a large about of strain within the ring (specifically transannular strain between the hydrogen atoms adjacent to the carbonyll oxygen) is stabilised by interactions between the pi* C=O bond and the sigma C-H bond. On the other hand this destabilisation and stabilisation within molecule 9 still has a larger total energy than molecule 10 which is present in the chair confomer. Molecule 9 has a carbonyl group which faces upwards, leading to both of the cyclohexane group and the cyclopentane rings both pointing down, generating of steric hinderance in the molecule. The main contributions to the energy of molcule 10 are present in the bending (10.7407kcal/mol), torsion (19.5764kcal/mol) and 1,4-Van der Waals (12.5740 kcal/mol) components of the energy. For bending, his means there is a large deviation from the desired bond angle, which, in this case is the angle within the highly strained ring which ideally would like to be 120˚. However in molecule 10 this angle is found to be 110.7˚, thus leading to the large bending energy value. The difference in the torsion is due to deviations from the ideal dihedral angle. The dihedral angle in molecule 10, between the carbonyl oxygen and the hydrogen on the alpha carbon, was found to be 41.9627˚, different to the ideal value of 60˚, thus again creating an energy difference. The final main contribution is from the 1,4-Van der Waals caused by steric repulsions between the methyl hydrogens at the top of the bridge clashing with the hydrogens in the heptane ring).
The alkene reacts slowly because it is a "hyperstable olefin" [3] . A hyperstable olefin is one in which the alkene contains less strain than the parent alkane. This means that, as they are lower in energy, they will be fairly reactive. This is due, according to the literature, to the hyperstable olefin having a negative "olefin strain" value. The value is negative because the olefin is lower in energy to than the parent alkane. Following the literature, which describes the olefin strain as extra strain associated with the presence of the double bond, a reaction of the alkene is slow due to the extra stabilisation. In the case of the taxol molecule the reaction will also be effected by sterics due to the methyl groups attached to the bridge. In order to speed up the reaction of the alkene, reaction conditions would have to optimised to ensure attack of the molecule was not hindered by the methyl groups on top thus changing the equilibrium of the reaction by driving the reaction to form another product.
Key literature
- Elmore, S.W; Paquette,L; Tetrahedron Letters, 1991, 319; DOI:10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0
- Vinter, J.G; Hoffman,H. M. R.; J. Am. Chem. Soc., 1974, 96, 5466 (DOI:10.1021/ja00824a025 DOI:10.1021/ja00824a025 ) and 95, 3051 for another nice example of atropisomerism.
- ÊIslas-Gonzalez,G.; ÊBois-Choussy, M; ÊZhu,J; Org. Biomol. Chem., 2003, 30-32. DOI: 10.1039/b208905.
- Stephane,L; Papamicael,C; Marsais, F; Dupas, G; Levacher, V. Tetrahedron: Asymmetry, 2004, 15, 3919-3928. DOI: 10.1016/j.tetasy.2004.11.004
Regioselective Addition to Dichlorocarbene
As a result of the aforementioned problems with the MM2 method, a different method of analysis was used: The MOPAC Interface. This interface works by taking into account the influence of the electrons on the molecule and consequentially spectroscopic properties.
Part 1:Orbital Control of Reactivity
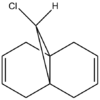
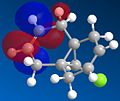
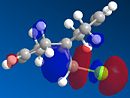
Molecule 12 can react with a range of elecotrophiles such as per acids and dichlorocarbene. The MOPOC programme modelled molecule 12 by predicting the geometry of the molecule, calculating the energy of the orbitals and displaying the orbitals generated on the screen. The Molecule was first minised in enegy using MM2 to produce a total energy of 17.8971 kcal. Using the MOPAC PM6 method, orbitals were calculated:
 |
 |
 |
 |
 |
 |
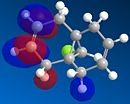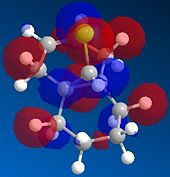
The same proceedure was run with the double bond which anti to the C-Cl bond being replaced with a C-C single bond. The energy was minismed using MM2 to give a value of 24.7880kcal/mol, higher than when the molecule contained the double bond. Following the proceedure the molecular orbitals were generated:
 |
 |
 |
 |
 |
 |
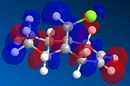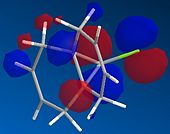
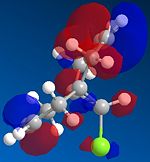
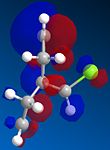
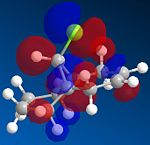
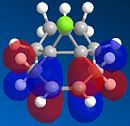
From the generation of the HOMO orbitals for both molecule 12 and the monoalkene it is possible to work out which molecule is more suscpetible to electrophilic attack. It is possible to see that in the dialkene (molecule 12) there is a large electron cloud present in the region between the carbon=carbon double bond syn to the C-Cl and the C-Cl bond. This is becuase the chlorine group is strongly electron withdrawing and the carbon=carbon double bond is electron rich. As a result of these factors there is a build up of charge, shown as the electron cloud, in the area between the Cl and the double bond syn to the chlorine. The monoalkene, however, does not have this large build up of charge.
It is also important to note that the HOMO-1 also contains a large electron cloud over the double bond anti to the carbon-chlorine bond. The LUMO of this molecule and the LUMO+1 are antibonding orbitals, and, as seen in the images, appear to have nodes (especially visible in LUMO+1 orbital picture). It should be also noted that the LUMO is similar in shape to the HOMO-1. This means that, if the energy levels are at the correct level, then electrons can pass from the HOMO-1 into the LUMO orbital. This donation will lower than the energy of the system, stabilsing it, but causing a weakening of the carbon-chlorine bond. With respect to the monalkene, none of the HOMO-2, HOMO-2, HOMO or the LUMO, LUMO+1, LUMO+2 look similar so the same process cannot happen. As this electron donation can not happen then the C-Cl bond will not be weakened due to more electrons in the antibonding orbitals, and therefore leading to a stronger C-Cl bond. This is investigated and proven in the section below.
From this analysis it is possible to say that molecule 12 is the more nucleophilic, due to the build up of the electron cloud between the double bond and the chlorine, and so will be more susceptible to electophilic attack. Electrophilic attack on this molecule will occur in the HOMO and HOMO-1 molecular orbitals as these molecules have the largest build up of electron density. It is also logical to attack here as the electron density is built up over the alkene double bond, which is an electron rich bond, and so would be susceptible to electrophilic attack. It can therefore be deduced that the monoalkene, without the build up of the electron charge between the chlorine and the double bond, is more electrophilic and therefore will be more susceptible to nucleophilic attack. The orbital which will be used in the nucleophilic attack would be the LUMO+1 because this orbital has little electron density over the molecule. The method does distinguish between the 2 alkene bonds because they are present in different environments and so the bonds will be different in nature and thus will be distinguished between in the computational method.
The Influence of the C-Cl Bond on the Vibrational Frequencies of the Molecule
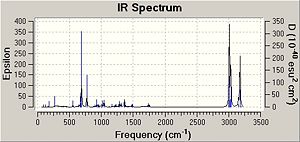
The C-Cl bonds were analysed to see the influence of the C-Cl bond on vibrational frequencies of the molecule. This anaylsis was done using the "density functional" approach.
| Bond | Molecule 12 | Molecule 12 Loss of ant C=C |
| Frequency cm-1 | Frequency cm-1 | |
| C-Cl | 770.86 | 779.93 |
| C=C (anti to Cl) | 1737.04 | - |
| C=C (syn to Cl) | 1757.34 | 1753.76 |
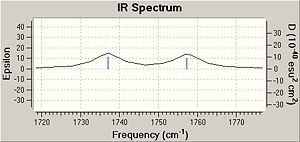
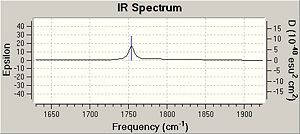
By comparing the IR it is possible to see that for molecule 12 there are 2 C=C bonds at 1737cm-1 for the bond anti to the chlorine and at 1757 cm-1, consistent with the literature values for such bonds [4]. Furthermore it is possible to see that the double bond anti to the chlorine is not present in the IR of the monoalkene, with only the presence of 1 double bond at 1753 cm-1. The higher values of the C=C frequencies are likely to be attributed to the presence of the electronegative chlorine in the molecule. Both molecules have C-Cl stretches at the expected frequencies.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
From earlier it was said that in molecule 12 the C-Cl bond is weaker than in the monoalkene due to donation of the electrons into the anti bonding orbital. This is seen in the IR spec for molecule 12 because the C-Cl bond in the monalkene is shifted up the specturm meaning that it is at higher energy. It should also be noted that the removal of the anti alkene is causes the energy of the syn bond to be lower, further backed up by the IR in which the syn frequency is higher in shift and thus in energy than the anti.
Key literature
Halton, B; Boese, R; Rzepa, H.S.; J. Chem. Soc., Perkin Trans 2, 1992, 447. DOI:10.1039/P29920000447
Structure Based Mini Project using DFT-based Molecular Orbital Methods: The Reaction of Norbornene Epoxide with Bismuth Nitrate in Dichloromethane
In order to determine between the 2 isomers, IR spectroscopy could be used to because of the different orientations of the ONO2 group. For example there will be different interactions of the OH group with the ONO2 group because in 37 there will be a bigger interaction between the OH and the ONO2 because they are closer. Different types of NMR could be run: Both Carbon and Hydrogen could be used. Furthermore 2D NMR methods could be utilised. NOESY, which determines between the hydrogen environments, could be used to determine between the hydrogens in the molecule. Other methods to be used could be HMBC, which gives long range C-H couplings (2-4), or HSQC, which measures C-H coupling in a shorter range. However one of the best ways would be to use coupling constants to determine the environments of the hydrogens. Another method would be to carry out analysis on optical rotation because the molecule contains 4 different chiral centres. However, the optical rotations of the isomers would only vary slightly because the chiral centres in the molecule are only slightly different, causing a small change in the optical rotations for the different isomers. Another method would be to analyse the dipole moment in both isomers. Isomer 36 would have a small dipole moment facing downwards (with respect to the image in the reaction scheme) due to the OH of the dipole on the top being counter balanced by the ONO2 group on the bottom of the molecule. In contrast isomer 37 will have a larger dipole moment out of the top of the molecule because both the OH and the ONO2 groups are on the same side of the molecule.
NMR Analysis
The aim of this mini-project was to investigate, using GIAO to predict the 13C spectra, the validity of data obtained from a scientific paper [5] , in this case by investigating the reaction of norbornene with Bismuth Nitrate in Dichloromethane:
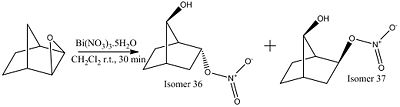
The isomer in which both the OH and the side chain face up is isomer 37, and the isomer in which the OH points up and the side chain points down in isomer 36.
The NMR data was obtained using the following method: MM2 was run on the molecule to minismise the energy. This process worked well becuase of the simplicity of the molecule and due to the constraints on the structure from the bridge in the centre of the molecule. Once the molecule was optimised, the SCAN input file was created where the DFT method used was DFT=mpw1pw91, the basis set was set to 6-31G (d,p). The file obtained was modified using a different heading and then re-submitted and the NMR data file obtained.
Please note that the number of the carbons start at number 2 to be consistent with the data obtained from the run scan, in which the NMR data does not include a carbon 1 but starts counting from carbon 2. The NMR reference was TMS mPW1PW91/6-31G(d,p) CDCl3 GIAO.
| Isomer 36 | ||
| Carbon Atom | Computational Results/ppm | Literature Values/ppm |
| 2 | 27.6619 | 26.8 |
| 3 | 43.4991 | 41.2 |
| 4 | 32.596 | 37.2 |
| 5 | 82.4481 | 86.5 |
| 6 | 20.027 | 23.6 |
| 7 | 44.7915 | 46.1 |
| 8 | 80.2247 | 78.7 |
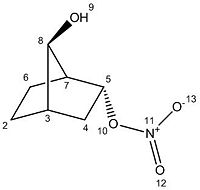
The MM2 mechanics produced an overal energy of the molecule to be 29.5163 kcal/mol with the majority of the energy split fairly evenly between the torsion and the bend energy subcatagories. The torsion is high due to the deviaitons from ideal dihedral angle within the molecules due to the strain generated by the bicyclic ring.
From the results obtained [6] it is possible to see that the computational method is in good agreement with the experiremental results obtained from the literature. The closeness of the literature results to the computationally calculated results is shown in the graph below.
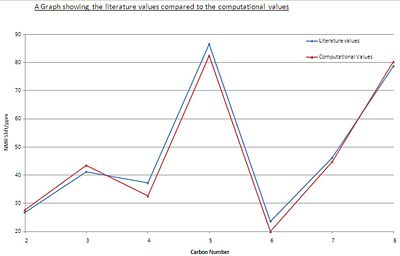
The graphs show that the difference between the 2 sets of data are small as both the lines follow the same pattern and are close to each other. However the differences are not consistent in that the computational is not always lower than the literature values, with some compuational data being lower than the literature values and some computational data being lower than the literature values. This difference is due to a systematic error and the error in carrying out the actual experiment, and it is not likely that there is an error in the computational method
The same method was carried out for the isomer number 37, in which both the side chain and the OH group are pointing up. It is important to note that the NMR analysis in this molecule started carbon numbering at 1 because the scan results started at number 1.
| Isomer 37 | ||
| Carbon Atom | Computational Results/ppm | Literature Values/ppm |
| 1 | 26.7526 | 26.7 |
| 2 | 43.7705 | 42.6 |
| 3 | 34.0198 | 37.4 |
| 4 | 84.2445 | 88.7 |
| 5 | 25.1716 | 24.4 |
| 6 | 46.0943 | 46.4 |
| 7 | 78.3061 | 81.3 |
The isomer 37 was optimised in geometry using the MM2 method yielding a total energy of 31.1880kcal/mol. The 2 main contributions to the energy were from the bending, similar to isomer 36, and torsion, again similar to isomer 36. These differences occur for the same reasons as in the other isomer: deviations from the ideal bond angles and dihedral angles.
From the results obtained [7] a good agreement between the computation values obtained by calculation and the literature value was found. This is shown in the graph below:
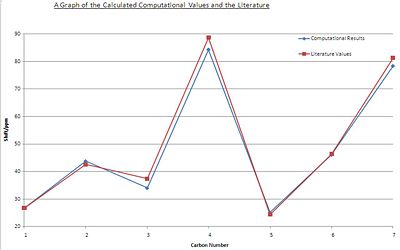
Predicting 3J H-H Couplings
The 3J H-H couplings were calculated using a website [8].
This method meant drawing out both conformations of the molecule as Newman Projections. The draw back of this process is that the ring carbons have to be drawn as CH2. Further limitations are that the groups have to be selected from a list for the positions on the projection. This is a limitation because the only things that can be selected are elements, therefore for the ONO2 group O was selected, for the CHOH group C was selected and for the CH2 group C was selected. This limitation will cause a big difference between the calculated coupling constants and the experimental coupling constants. Having said that the same pattern between the isomers should occur in both the computaiton analysis and the literature. Using ChemBio3D the dihedral angles for the isomers were measured: isomer 36 had a dihedral angle of 40.9982 degrees, and isomer 37 had a dihedral angle of 83.1948 degrees. The only important 3J H-H coupling is that of the hydrogen at the bottom of the bridge and the hydrogen on the adjacent carbon (which has the ONO2 group attached). This coupling will determine between the isomers. In isomer 36 the coupling value was determined to be: 5.71Hz. The literature value for the coupling of this H in the isomer is 7.9Hz. In isomer 37 the coupling constant was found to be 0.71Hz, with the literature value being 2.8Hz. Both of these values show that it is possible to determine between the 2 isomers because isomer 37 has a much smaller coupling constant for this hydrogen than isomer 36. This follows the same pattern as the literature which also has larger constants for isomer 36 than for isomer 37.
Predicting IR Spectra
The molecule was minimised using MM2 and then further minimised using the same DFT method as above. The data file produced was then recoded to specify the IR vibrations.
| Isomer 36 | ||
| Stretch | Computational cm-1 | Literature cm-1 |
| Scissoring C=O | 765.022 | 758 |
| C-C Stretch | 887.16 | 867 |
| C-C Twist | 942.926 | 935 |
| Scissoring C-C | 1015.83 | 1005 |
| Scissoring C-C | 1032.75 | 1037 |
| Scissoring C-C | 1114.46 | 1148 |
| C-H Twist | 1291.37 | 1282 |
| C-C Assymetric Stretch | 1742.2 | 1618 |
| C-H Stretch | no value present | 2882 |
| C-H Assymetric Stretch | 3004.17 | 2967 |
| OH Stretch | no value present | 3375 |
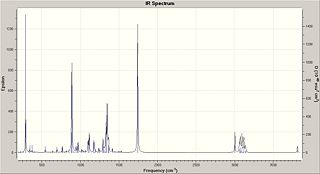
| Isomer 37 | ||
| Stretch | Computational cm-1 | Literature cm-1 |
| Scissoring N=O | 764.17 | 757 |
| C-H Twisting | 863.882 | 865 |
| C-C Asymmetric Stretch | 975.637 | 966 |
| C-O Stretch | no peak found | 1068 |
| C-C Twisting | 1078.44 | 1085 |
| C-H Rocking | 1147.27 | 1157 |
| C-H Twisting | 1275.33 | 1279 |
| C-C Asymetric Stretch | no peak found | 1625 |
| C-H Assymetric Stretch | no peak found | 2925 |
| C-H Assymetric Stretch | no peak found | 2965 |
| OH Stretch | no peak found | 3343 |
The computational data obtained [9] does not have some peaks found within the literature values. These peaks which are only present in the literature values may be of small concentrations of contaminants. More likely however is that they are due to interactions between the isomer and the solvent used in the preparation of the IR (eg. nujol mull). Furthermore these stretches may have been taken into account in an earlier stretch and already been shown in the spectrum. The same method for isomer 37 was followed and the IR spectrum obtained from the data. The data obtained [10] was found to be not as good as that for isomer 36: the calcualted spectrum contians many areas of peaks that are not present in the literature, and the literature contains areas of peaks that are not present in the computational results.
For example the computational results did not produce peaks at 1625 cm-1, 2925 cm-1, 2965 cm-1 and 3343 cm-1. There are no peaks on the computational spectrum around 1600, a region consistent with a C-C in a ring [11], which is of concern because there are many C-C present in the molecule. No lines at 3343 cm-1, a region consistent with OH peaks would be a concern, however there are peaks present at a lower value which would correspond the OH stretch (3010-3150cm-1).
On the other side the computational spectra produced large peaks at 887.131 cm-1, 1335.19 cm-1, 1747.68 cm-1, and 3817cm-1 which were not present in the literature. These correspond to C-H stretch, C-H stretch, O-N stretch and OH stretch respectively.
These differences between the literature spectra and the data obtained computationaly may be caused by the 8% bending error at the higher frequencies. This may explain why the computational value 3817cm-1 obtained, which was not found in the literature, could be decreased down to the literature value of 3343 cm-1 (which was not seen in the computational value) meaning that the computational results would correspond to the literature.
Mechanistic Considerations
The mechanism is as follows:
The mechanism proceeds via a non- classical carbonium ion. These carbonium ions contain 3-centred-2-electron bonds within the bicylic system with a delocalised sigma bond [12], shown in step 3 of the mechanism. The mechanism follows a Wagner-Meerwein rearrangement, shown in the mechanism where the Bismuth moves from the ring to the bridge. This shift leaves a positive charge on the carbon on the ring and here is where the nucleophile attacks, generating the 2 isomers produced: either the nucleophilic ONO2 attack above or below the molecule. This mechanism stops the reaction of a simple opening of the epoxide ring to form the trans ring-opened porduct.
Conclusion
Overall the computational analysis of the molecule was found to be a success because the results obtained from the computational method were close to the literature values found. Having said that the values obtained for the NMR calcualtions were much closer to the literature than the calculated values of IR, proving that the computational method has its shortcomings. Optical rotation data was not run because there will only be a small difference between the different isomers, and furthermore no literature values could be found to help decifer between the 2 different isomers.
Key literature
- Cavdar, H and Saracuglu, N, Eur. J. Org. Chem., 2008, 4615-4621. DOI:10.1002/ejoc.200800481
References
- ↑ The Endo Addition Rule: {[1]
- ↑ Molecular Orbits and Bonding of Cyclopentadiene: {[2]
- ↑ Hyperstable Olefins: Further Calculational Explorations and Predictions, JACS 1986, 108, pp3951-3960: DOI:10.1021/ja00398a003 ]
- ↑ Infrared Spectroscopy {[3]
- ↑ Synthesis of New β-Hydroxy Nitrate Esters as Potential Glycomimetric or Vasodilators, Euro. J. Org. Chem. 2008, pp4615-4621: DOI:10.1002/ejoc.200800481 ]
- ↑ Data file for Isomer 36 DOI:10042/to-2916 ]
- ↑ Data file for Isomer 37DOI:10042/to-2917 ]
- ↑ Method for calculating coupling constants [4]
- ↑ Data file for IR of Isomer 36DOI:10042/to-2928 ]
- ↑ Corresponding IR stretches to wavenumbers [{http://en.wikipedia.org/wiki/Infrared_Spectroscopy_Correlation_Table}]
- ↑ IR DOI:10042/to-2928 ]
- ↑ Advanced Organic Chemistry 4th Edition [5]