Introduction

As computational chemistry is an extremely powerful tool for understanding and investigating transition states, molecular geometry, chemical reactivity and even biomolecules like enzymes, it is widely and ever increasingly utilised by people working in all areas of Chemistry. [1] Gaussian, a popular computational chemistry programme, can be used to look at transition states. Transition states cannot be isolated and are extremely difficult to study using spectroscopic techniques, as they have very short lifetimes. This makes Gaussian a powerful tool in the study of transition states. ‘Exploration’ of part of the potential energy surface (PES) is key to how Gaussian finds transition states.

Potential Energy Surfaces
To make theory closer to experiment we must examine all possible structures for a given chemical formula.[2] A complete PES shows the potential energy of a set of atoms in all possible atomic arrangements. An example of a PES is given in figure 1. A PES has 3N-6 coordinate dimensions, for a non-linear molecule. These are related to the molecule's degrees of freedom. This is because any 3-dimensional system containing N atoms can be defined by 3N coordinates. As the overall whole-body translation or rotation of a system, e.g. a molecule, does not concern us we can subtract 3 coordinates for the translation and rotation respectively. [3] This means the PES for any non-linear molecule with N atoms can be defined as a function of 3N-6 coordinates. As the number of dimensions, we work in is greater than 3 we must work in Hilbert space. On this PES we can locate both stable structures (products and reactants) and transition states. There are many stable structures situated at local minima; stationary points where displacements in any coordinate lead to an increase in energy. Transition states are located at saddle points. These are also stationary points. However unlike the stable structures, displacement in any direction in one certain coordinate leads to a decrease in energy. This means it is a minima in every reaction coordinate but one, in this reaction coordinate it is a maxima. This 1 coordinate is selected as the reaction coordinate. Therefore along the reaction coordinate, r, we can say that:

This is true for both stable structures and transition structures:

This is true for only the transition structure, as the curvuture is negative at a maximum (the only way is down!):

This allows us to distinguish between stable and transition structures using the second order derivative. A Hessian matrix, one made up of second order partial derivatives, describes the curvature of our PES. Only positive Hessian eigenvalues indicate a stable structure. Whilst one single negative eigenvalue points to a transition structure. Gaussian computes the eigenvalues to find these structures. These eigenvalues are force constants, k, which are related to the vibrations of the molecule. Using Hooke’s law, the frequency of these vibrations can be calculated by Gaussian:

Hooke’s law:

When we have a transition state for one of the frequency calculations we are forced to square root a negative number, this means an imaginary frequency is obtained. Somewhat confusingly this is shown as a negative frequency on Gaussian. The presence of one negative frequency is indicative of a transition structure, whilst only positive frequencies indicate a stable structure.

Nf710 (talk) 09:40, 21 February 2018 (UTC) This is excellent well done. Great understanding of the hessian matrix.

Method

Exercise 1:
Reactants were first optimised using the PM6 method. Then the reacting terminal C-C bond lengths were frozen with a distance of 2.2 Angstroms (an intermediate distance between unbonded and singly bonded carbons) and re-optimised to a minimum using PM6. The resultant was used to find the transition state. An IRC was used to confirm that the correct TS was obtained. The resulting product was optimised again at the PM6 level.

Exercise 2:
The same method as the previous exercise was used, however after initial PM6 optimisation the reactants, transition state and products were all reoptimised using B3YLP [6-31G(d)].

Exercise 3:
Here it was difficult to guess a transition state to optimise, as multiple products could form from the reactants. So we went from products to reactants instead of the other way around. This allowed the location of each transition state. All calculation were performed using PM6.
PM6: This is a semi-emperical method so it uses some parameters obtained from experiment. This means it is very quick.
B3YLP [6-31G(d)]: This is an ab initio method and involves solving the time dependent Schrodinger equation. As it uses no experimentally obtained data and calculates everything from scratch. It is computationally expensive. As the Schroedinger equation is extremely difficult to solve some approximations must be made. A major one of these is the Born-Oppenheimer approximation, this states that as electrons move relatively fast compared to nuclei, nuclear motion can be effectively ignored. The 631-G(d) refers to the basis set. The larger this set the more accurate the approximations of the MOs involved. A larger set, of course, comes at the expense of computational power and time. [6]

Nf710 (talk) 09:53, 21 February 2018 (UTC) You are getting abit confused here. They do not use the time dependant SE. and all quantum chemical methods use The BO approximation. B3LYP is a DFT method and uses a HF calculation in the exchange correlation function.

Exercise 1: The Diels-Alder Reaction of S-Cis Butadiene and Ethene

(Fv611 (talk) Good exercise overall, well done on explaining the methodology thoroughly. You should have noted the symmetry of your TS MOs and could have discussed the bond lenghts at the transition state in a little more detail.)

Reactants

The simplest and most well known Diels-Alder reaction is the one between s-cis butadiene and ethylene. The reactants involved were first optimised (PM6) to minimums. The table below shows the minimum structures as well as the related HOMOs/LUMOs.

Ethene

Ethene MOs

Butadiene 1st Optimisation

Butadiene 2nd Optimisation

Butadiene MOs

Butadiene had to be optimised twice as the first optimisation structure had an imaginary frequency associated with it. This imaginary frequency arises as butadiene exists as a dynamic molecule moving between two bent structures, as the JSmol shows. It is momentarily planar as it transitions between the two bent structures. However in a DA reaction it reacts in it's planar form.

The Transition State

After optimisation, the transition state was successfully found (confirmed by 1 single imaginary vibrational frequency at 948.34i cm^-1, that showed a transition from reactants to products).

Transition state

Transition state MOs

Given this information the MOs were decomposed into their respective atomic orbitals (the reverse of LCAO), these atomic orbitals alongside the calculated energies were used to generate an MO diagram:

From the MO diagram we can conclude that AS-AS and S-S interactions are allowed but AS-S reactions are forbidden. There is a non-zero orbital overlap for S-S and AS-AS interactions and a zero orbital overlap for AS-S.

An IRC calculation was then conducted to follow the path between the reactants and products. Additionally it was used to monitor the carbon-carbon bond lengths throughout the reaction.

IRC	Animation of the Reaction
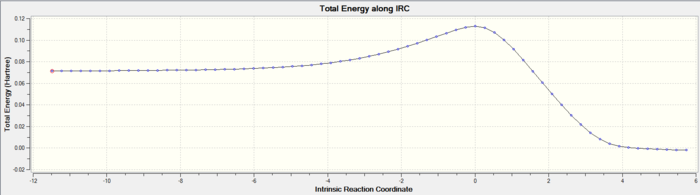
	Must be clicked on to open animation

C-C Bond Lengths	Carbon Atom Numbers

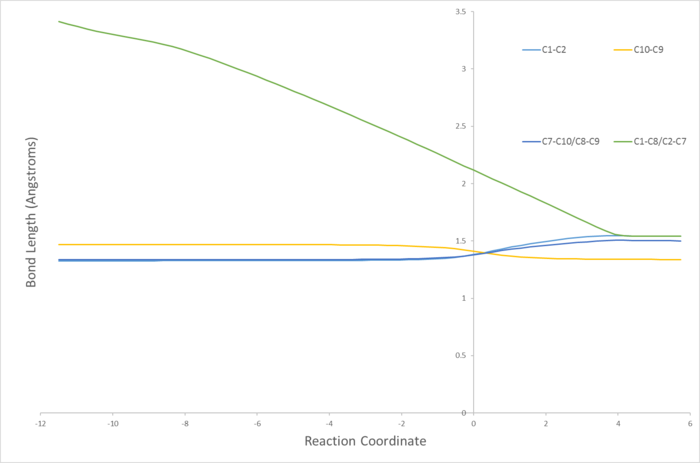
C-C Bond Length Analysis
Typical bond lengths, reported in literature[4], for sp³-sp³ and sp²-sp² are 1.542 Å and 1.338 Å respectively. The Van der Waal's (VDW's) radius of carbon is 1.7 Å [5]. From the bond length diagram it can be seen that at the start of the reaction the terminal carbons from each reactant (C1,C2,C7 & C8) are approximately 2 VDW radii apart. As the reaction progresses this decreases to about the length of a typical sp³-sp³ C-c bond length, indicating the formation of a single bond, as expected. Bond length between C1 and C2 decreases as the bond changes from a double bond (sp²-sp²) to a single bond (sp³-sp³). The bond lenght between C9 and C10 shortens indicating the formation of a double bond. From both the bond lengths and the IRC movie it is also clear that the formation of the 2 bonds at the terminal carbons is synchronous. At the TS (reaction coordinate=0) whilst the other bonds are almost at their final lengths the C-C terminal single bonds are far from their final lengths. They are properly formed after the transition state.

Product

The resultant product of the reaction was cyclohexene. An imaginary frequency was found in the initial optimisation. After symmetry breaking and reoptimisation this imaginary frequency was eliminated. The product was found to exist in a half-chair conformation:

Cyclohexene optimisation 1

Cyclohexene optimisation 2

Exercise 2: Cyclohexadiene + 1,3-Dioxole

Reactants

Cyclohexadiene and 1,3-Dioxole form an exo and endo product via a Diels-Alder reaction. This reaction was studied using Gaussian, via the method set out previously. Both reactants were first optimised using PM6 and then reoptimised using B3YLP [631G (d) basis set].

Cyclohexadiene

1,3-Dioxole

Transition States

(Fv611 (talk) The MO diagrams are generally correct, even though the energies of the endo conformation seem a bit off. You should be labeling your TS MOs consistently between the Jmol table and the diagram.)

Endo

Exo

These alongside the energy levels were used to produce the following MO diagrams for both the exo and endo TSs:
End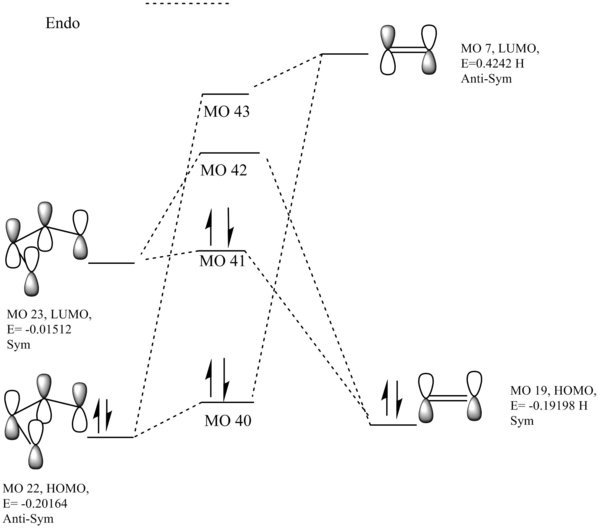o: Exo: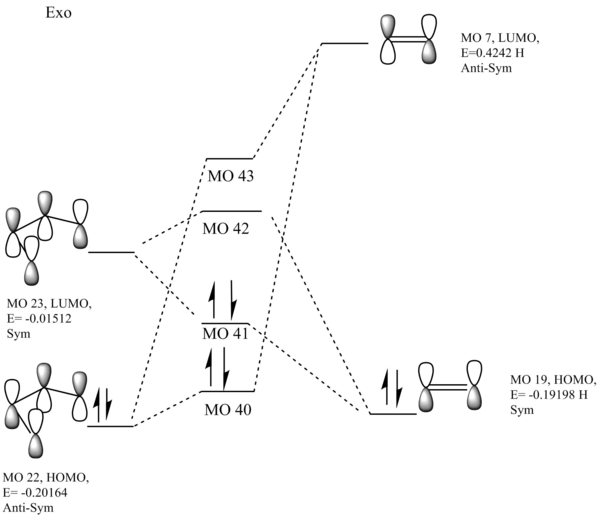
The interacting orbitals essentially look identical to Exercise 1, so these were adapted from the MO there. However from these MOs a key difference can be seen. This is that the dienophile's MOs are far higher in energy than the equivalent dienophile in exercise 1. This could be down to donation of electron density (lone pairs) from the oxygen p-orbitals into the diene. This increase in energy leads to an inverse demand Diels-Alder reaction. The HOMO of the dienophile is closer in energy to the LUMO of the diene, so can interact far better with it i.e better mixing. This means electrons 'move' from the dienophile to the diene, which is the opposite of a standard DA reaction.

Nf710 (talk) 09:58, 21 February 2018 (UTC) You cant compare the energy of the frontier molecular orbitals like this. They need to be in the same window. As they have different relative energies in this case.

Products

Endo

Exo

IRC

	Endo	Exo
IRC Animation
IRC Pathway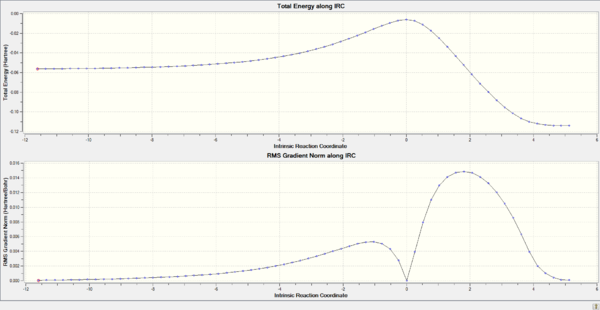

Analysis

To determine which of the 2 products were the kinetic product and thermodynamic product, the sum of electronic and thermal free energies were extracted from the reactants, TSs and products all at 631-G(d). These were then converted from Hartree/Particle to KJ/Mol. The table below displays this data:

Molecule (B3YLP 631-G(d))	Energy (KJ/Mol)
Cyclohexadiene	-612584.418806
1,3-Dioxole	-701187.43398
Endo TS	-1313622.16514
Exo TS	-1313614.32277
Endo Product	-1313849.3733
Exo Product	-1313845.77899

	Endo	Exo
Activation Energy (KJ/Mol)	149.68786	157.53023
Gibbs Free Energy (KJ/Mol)	-77.5203	-73.92599

It is clear from this that both the thermodynamic and kinetic product is the endo one.
The lower activation barrier can potentially be explained by the stabilisation of the TS via secondary orbital interactions. From the MO diagrams p-orbital interaction of the oxygen (circled) with the diene can be seen:

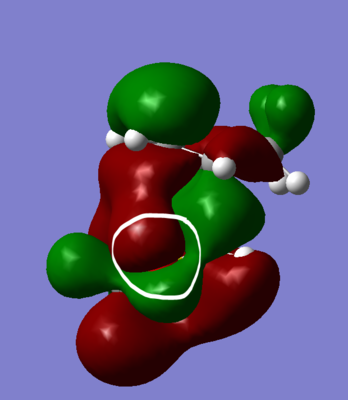
The thermodynamic stability of the endo compared to the exo might be down to the increased hydrogen-hydrogen steric clash that the exo suffers from as it's CH2 groups are on the bridgehead whereas in the endo they face away:

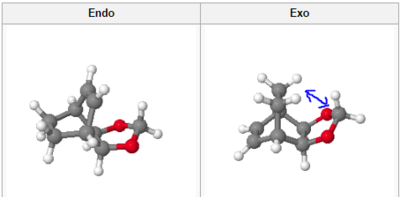
Nf710 (talk) 10:05, 21 February 2018 (UTC) Your reaction energies are about 10 KJ out but you have still come to the correct conclusion and you have some nice diagrams. However you could have gone into more detail on the discussion.

Exercise 3 O-Xylylene + SO2

Transition States and Reaction Pathways

Endo Diels-Alder

Exo Diels-Alder

Cheletropic

Transition State

IRC

IRC Animation

The IRC animations show that the formation of the C-S and C-O bonds are asynchronous. The C-O bond forms first.

Energy Calculations

Molecule (PM6)	Energy (KJ/Mol)
/ O-Xylylene LOG	467.417801
/ SO2 LOG	-311.4210807
Endo TS	237.7653
Exo TS	241.748182
Cheletropic TS	260.084675
/ Endo Product LOG	56.9891073
/ Exo Product LOG	56.3274813
/ Chelotropic Product LOG	0.000482426537

	Endo	Exo	Cheletropic
Activation Energy (KJ/Mol)	81.7685797	85.7514617	104.0879547
Gibbs Free Energy (KJ/Mol)	-99.007613	-99.669239	-155.9962379

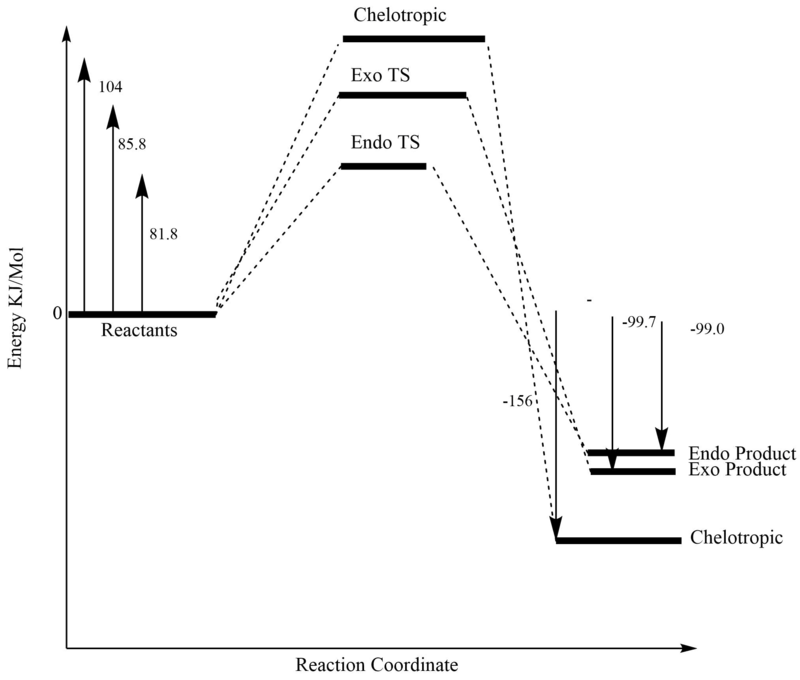
Activation energies The activation energy differences can be explained by the fact that the transition state involves the formation of a 5-membered ring, which are known to be more strained than their 6-membered counterparts. Endo, as often is the case, is stabilised by secondary orbital interactions. However the magnitude of these must be small as their is no significant difference in the endo/exo activation energies.
Gibbs Free Energies The chelotropic product contains 2 strong S=O bonds as opposed to only one present in the DA products. This may be the cause of it's thermodynamic stability.The thermodynamic driving force in the DA reactions maybe the formation of an aromatic benzene system, allowing the xylene to escape from it's anti-aromaticity (4pi e-). There is no large difference in the thermodynamic stability of the exo and endo DA products.

(This section is a bit too brief Tam10 (talk) 15:27, 19 February 2018 (UTC))

References

[1] Computational Chemistry by Errol Lewars ISBN: 978-90-481-3862-3 (2011)
[2] Essentials of computational Chemistry (2nd edition) by Christopher J Cramer
[3] Introduction to potential energy surfaces and graphical interpretation by Ralph Jaquet (2002)
[4] HJ Bernstein, Bond distances in hydrocarbons, Trans. Faraday Soc., 1961,57, 1649-1656
[5] Intermolecular Nonbonded Contact Distances in Organic Crystal Structures: Comparison with Distances Expected from van der Waals Radii, R. Scott Rowland* and and Robin Taylor*, The Journal of Physical Chemistry 1996 100 (18), 7384-7391, DOI: 10.1021/jp953141
[6] https://www.shodor.org/chemviz/optimization/students/background.html. Accessed February 2018.