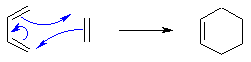Rep:Modtransitionstates jb2813

Transition states and reactivity

Introduction

The transition state of a reaction is a particular configuration along the reaction coordination which corresponds to the greatest potential energy along the reaction coordinate. At this point all reactant molecules which are colliding form to make products. We use their Hammond Leffler Postulate to estimate and predict the transition states [1], therefore the transition state responds to the state which it is closest in energy to, for example a late transition state is known as an endothermic reaction as the transition state is closer in energy to the products. Using computational analysis we are able to calculate energy, bond angles and lengths along with further physical data.

In this experiment of transition states and reactivity two methods were used to analyse transition states; using the Hammond Postulate to predict transition states and optimizing, at different levels, to a minimum The different levels used represent the degrees of accuracy to which the structure was optimized. HF/3-21G and B3LYP/6-31G* were used, the first of which is much quicker and less accurate. QST2 method was used at different levels of accuracy, which used labelling on the reactants and products, therefore calculating the resulting transition state which was associated with both reactants and products.

This experiment concentrates on different conformers of 1,5-hexadiene ie in anti/gauche linkage or chair/boat. The Cope Rearrangement will be studied to find the lowest energy transition state in which the reaction can proceed. Resulting from this Diels-Alder reaction will be run and calculated with different combination of molecules. [2]

Nf710 (talk) 15:35, 15 December 2015 (UTC) Well rounded intro. Could have had more information about about the computational methods used

Cope Rearrangement Tutorial

The Cope Rearrangement is a concerted pericylic reaction, which follows a  [3,3]-sigmatropic rearrangement of 1,5-dienes [3]. Throughout this task it can be shown to follow a transition state stage that is energetically and structurally equivalent to a diradical. The Cope Rearrangements proceeds via a thermally allowed Huckel reaction with 4n+2 electrons which, due to suprafacial components, results in disrotation of the molecule.

Optimizing the Reactants and Products

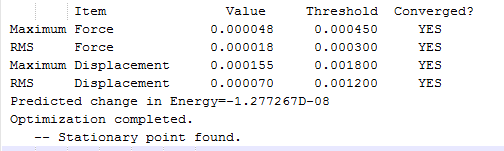
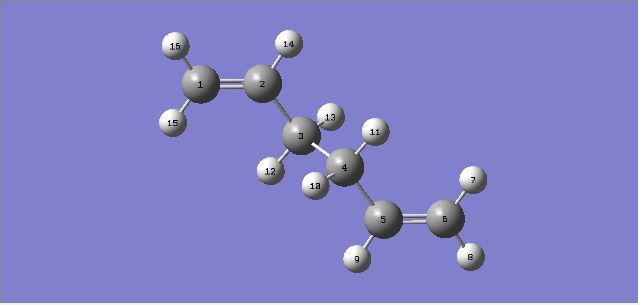
The structure, 1,5-hexadiene was drawn in two different conformers. Gauche and anti conformation with dihedral angles of 60 and 180 degress respectively. With each conformation, I have provided I screenshot with the energy, point group and an observance of the convergence of the force.

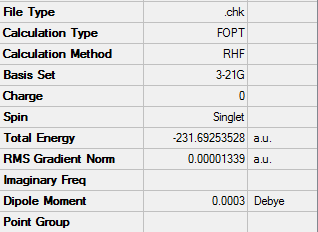
1,5-hexadiene with an anti linkage

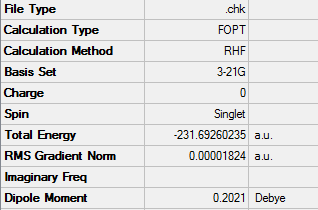
Using the Hartree–Fock method [4], determines the energy of system and the wavefunction in a stationary state, the basis set of 3-21G [5] which is the linear combination of set functions. The resulting energy from this optimization is equal to -231.69260235 au.

Using symmetrize function and keeping the tolerance at default the point group can be found The tolerance setting can be used to relax or tighten the symmetry that can be identified with the specific molecule in place [6]

.

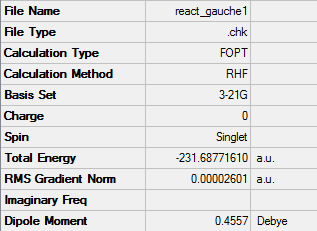
1,5-hexadiene with a gauche linkage

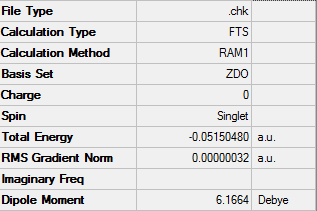
The energy for 1,5-hexadiene with gauche linkage after the optimization was -231.68771610au

The point group for the molecule was C2

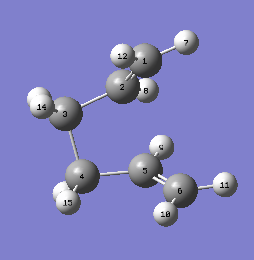
Gauche linkage 3

Due to the attractive interaction between C-C pi orbital and a vinyl proton, the lowest energy conformation of 1,5 hexadiene would be the gauche 3 linkage, meaning therefore it has the highest abundance out of all the conformers. This can also be seen by comparing the relative energies of all the structures when optimized.

.

The energy is equal to -231.69266120 au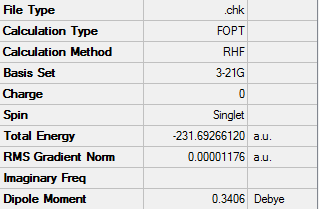

After optimization the point group is C1 after the tolerance was set to 0.01.

Nf710 (talk) 15:44, 15 December 2015 (UTC) You are correct in your discussion however you could have shown this by having the orbitals from the .chk file

Comparison of accuracy methods of optimization with anti 2

Using the same conformer, in this case the anti linkage 2 of 1,5-hexadiene, it is possible to directly compare the energy and other physical properties once the structure has been optimized at both levels.

At the HF/3-21G level;

The energy is -231.69253528au

The point group is Ci

At the B3LYP/6-31G* level

The energy was -234.61171166au

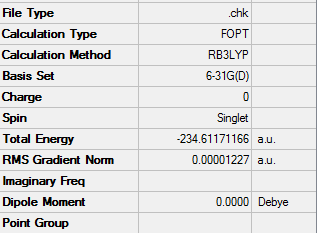
The point group remained the same as Ci

The convergence and force constant data;

Frequency and Geometry analysis

Optimizing the 2 anti linkage 1,5-hexadiene molecule, at different levels of accuracy result in different bond lengths and dihedral angles in the structure between the carbon atoms.

When using the less accurate HF/3-21G method the carbon-carbon double bond at the end of the structures is much shorter than if using the more accurate method. Literature values state a length of 1.33 Å which is much closer to the B3LYP/6-31G value. For the single bonds in the middle of the molecule, both methods predict similar lengths. Because of the ability of B3LYP/6-31G to predict bond lengths of unsaturated molecules closer to the literature value, it is much more accurate but more time consuming to use this method.

The dihedral angles for the B3LYP/6-31G are slightly larger than that of HF/3-21G, with B3LYP/6-31G closer to that of the ideal sp2 hybridised carbon centre. However because this is an 'ideal' angle, this cannot be used in this instance.

The frequencies are related to the second derivative of the PES, potential electronic surface, with respect to the geometric changes that I have discussed earlier. Therefore, using this second derivative, stationary points can be found from the structure when optimised, either at a maxima or minima. Imaginary frequencies occur when the numbers are 'negative' in gaussview, due to the harmonic oscillator equation </math>ω=(k/μ)sqrt</math> MAKE BETTER which correspond to a maxima, opposite for positive frequencies. When one single 'negative' frequency occurs when optimizing a transition state this is known as an imaginary frequency.

From my Anti 2 1,5-hexadiee optimized molecule, the results are as follows;

1 Hartree = 627.509 kcal/mol

Sum of electronic and zero-point Energies = 234.469215 (Hartree)

Sum of electronic and thermal Energies = 234.461866 (Hatree)

Sum of electronic and thermal Enthalpies = 234.460922 (Hartree)

Sum of electronic and thermal free Energies = 234.500800 (Hartree)

All frequencies are positive which from earlier in this report suggest that the structure is at minimum energy after optimization.

At different temperatures, ie 0K,

Nf710 (talk) 15:56, 15 December 2015 (UTC) You could have tabulated your geometry analysis. and gone into a bit more detail actually giving some numbers. However excellent understanding about the force constants link to the SHO equations although you could have formatted the equation better.

Optimizing the "Chair" and "Boat" Transition Structures

The Cope rearrangement involves the [3,3] shift of a sigma bond in the thermally activated molecule. We are assuming that the the transition state species is aromatic therefore having a large amount pf delocalisation meaning that the sigma bond is able to move, as bonds break and form at the same time. There is also another theory in which bond breaking and bond making are consecutive steps which are separated by a diradical intermediate. The transition state species has a C2h symmetry in a chair-like geometry with a four carbon centre. Using gaussview we can work out the geometry of the transition state species, whether it be boat or chair.

Nf710 (talk) 15:58, 15 December 2015 (UTC) good knowledge of the proposed reaction scehemes

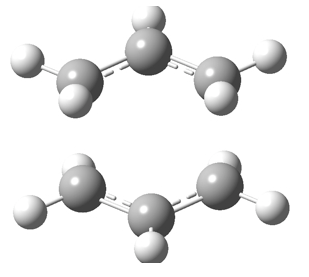[7] This is the chair transition state

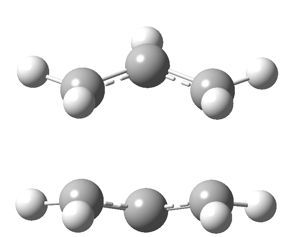[8] This is the boat transition state

Allyl Fragment

This is a CH2CHCH2 allyl fragment, it has been optimized using HF/3-21G, which looks like half of either the boat or the chair transition state. After creating a chair-like transition state, it is then optimized. 'OPT' is used, which requests that a geometry optimization is performed. Then the force constant matrix can be calculated using an empirical estimate of the Hessian and the starting transition state guess.

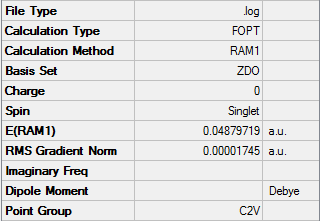
The results from optimizing the allyl fragment at the HF/3-21G level are as followed;

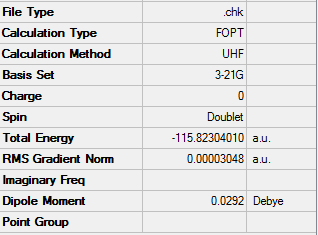The energy from the optimization is -115.82304010au

The point group after the optimization is C2v

Chair Optimization at the HF/3-21G level

From the earlier allyl fragment, a chair transition state was created with the fragments 2.2 Å away from eachother, changing the point group from C2v to C2h point group. This was then optimized and a frequency analysis was conducted, optimization was changed from minimum to TS (Berny), an algorithm which optimizes to transition states and higher-order saddle points. [9]

Opt+Frequency log file is here

The energy for the chair optimization;

The imaginary Frequency is shown below

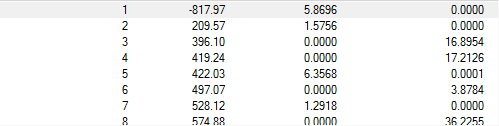
The animation of the chair strcture.

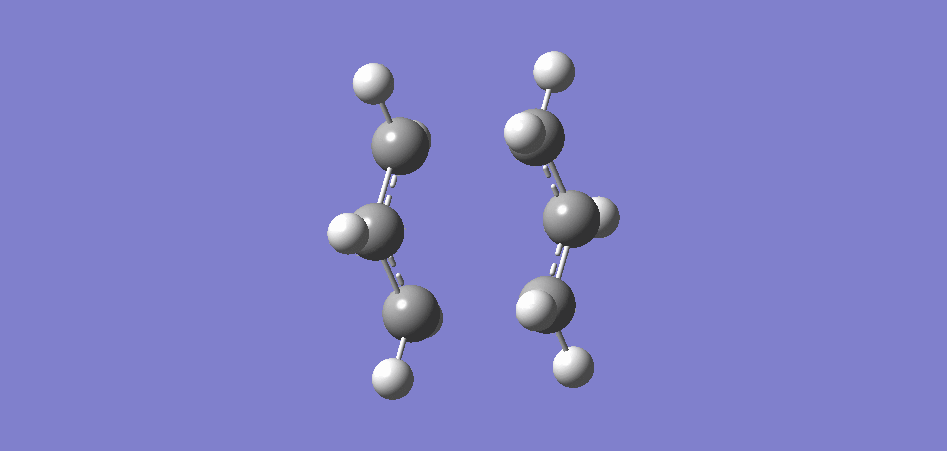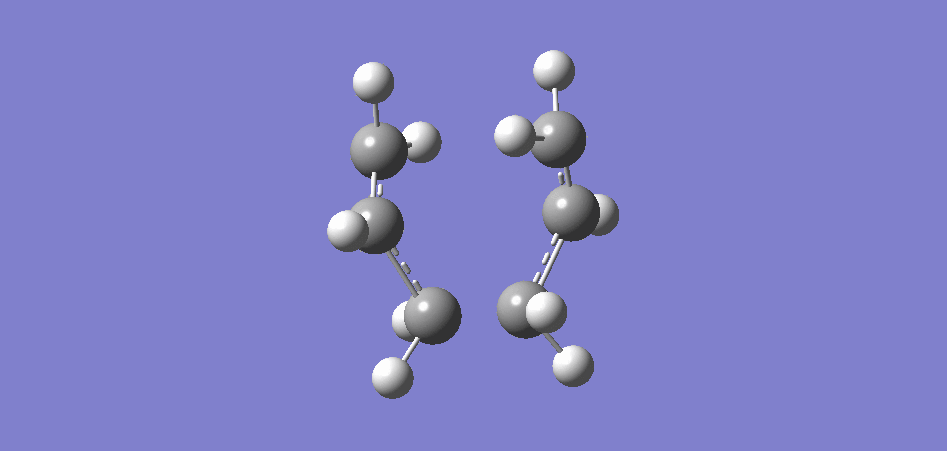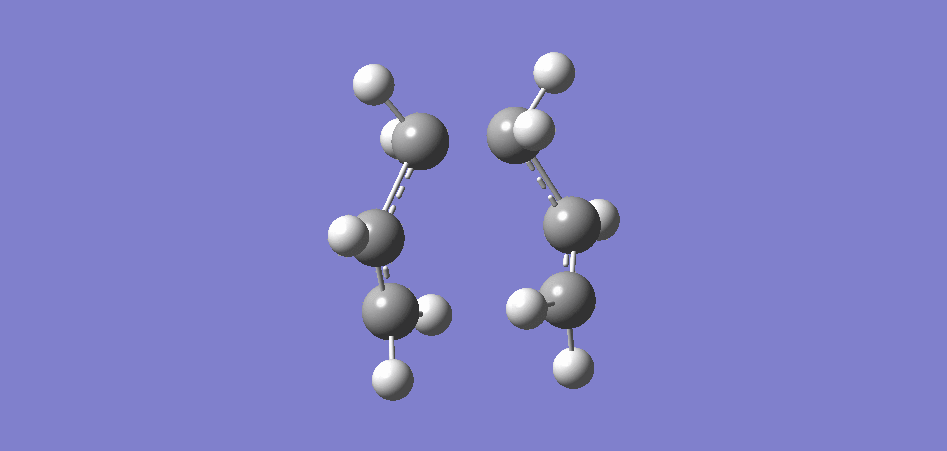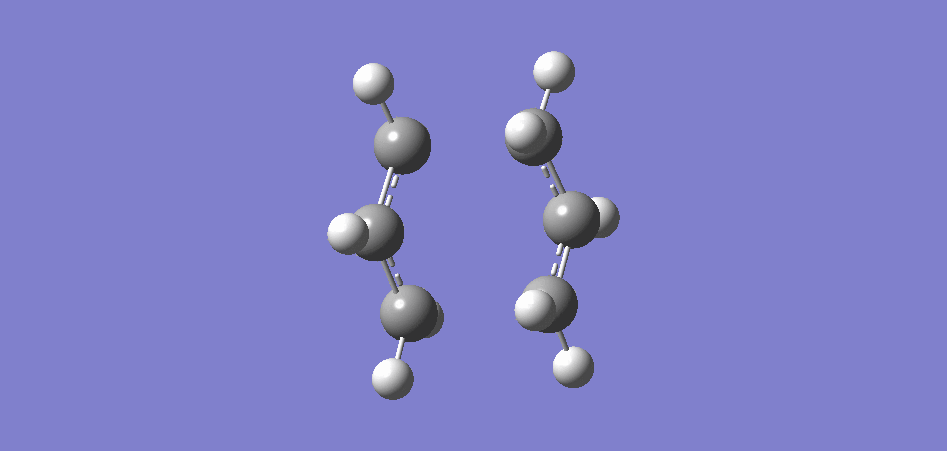
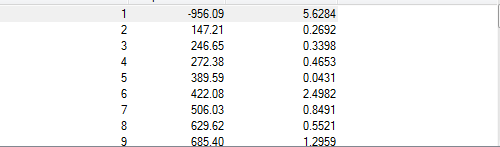
From the frequencies analysed, we can see that one value of -817.97cm-1 is a 'negative' or imaginary value. This suggests that the stationary point is at a maxima. This point is maximum along one direction, shown in the animation, however it is at a minimum in respect to every other direction. Therefore this point is a 'saddle point'.

Nf710 (talk) 16:09, 15 December 2015 (UTC) Correct frequency and good understanding of the berny mechanicism

Chair Optimization when Coordinates are Frozen

Using this method essentially means that the fixed ends remain at 2.2 Å whilst the optimization takes place, the rest of the molecule is allowed to move freely. This structure was then optimized again with the ends being unfixed and the whole molecule able to move, even though this is only slightly as the optimization process is almost complete.

The log file for Opt and frequency is here

Both structures have used HF/3-21G level of theory, however in freezing the coordinates of the ends the bonds are very slightly longer, albeit by 0.0004Å and the imaginary frequencies are also very similar both very close to -818. Therefore the structures are very similar and using the frozen coordinate method in this circumstance does not increase the accuracy of results, using a higher level of theory may have increased the accuracy.

QST2 optimization of boat transition structure

This method requires precise labeling of the products and reactants, when the optimization is run the transition state resulting from the reactants will be obtained.

Insert Labeling diagram

Here is the precise labeling for the reactants;

]

Here is the precise labeling for the products

However using this labeling system, instead of a cope rearrangement the bond between carbon 3 and carbon 4 broke, therefore resulting in a formation of two allyl fragments. Rotation around the bond that was broken, in turn, allowed the Cope Rearrangement transition state to be found.

After the rotation around the bond the labeling system looked as follows;

Reactant labeling;

Product labeling;

Using these structures, the boat transition state structure was formed as shown below;

There, again, is one imaginary frequency at 839.97cm-1 which shows a maxima stationary point.

Nf710 (talk) 16:23, 15 December 2015 (UTC) All your frequencies here are correct

Intrinsic Reaction Coordinate

This method produces information relating to at which point in the reaction each conformer of the transition state is produced. Using the optimized chair conformation, this process can be calculated and analysed. The step size of each iteration determines the accuracy of the result. Only the forward direction needs to be computed in this case, due to the symmetry of the reaction coordinate, as both products and reactants have the same structure.

From the ICR graph, at 0 reaction coordinate that potential energy surface is at a minimum, the RMS plot also shows this.

Nf710 (talk) 16:31, 15 December 2015 (UTC) there is no graph here

Activation Energies

Reoptimizing the boat and the chair structures oringially from the HF/3-21G level now to the more accurate B3LYP/6-31G level of theory can show us the activation energies for the reaction via both transition states.

For the boat transition state, the calculation summary at the B3LYP/6-31G level is as follows;

The point group is C2v

For the chair transition state; The energy is -234.55693218au and the point group is C2H.

Optimized transition state geometries different....Higher theory level correspond to TS....

Activation energy is calculated by subtracting the appropriate energy away for the Reactant (Anti2) energy. From the results given in the appendix [10]

From the results table it is possible to deduce that the higher level of theory, B3LYP-631G, values are much closer to the experimentally observed values, meaning a higher level of accuracy. From the activation energies it is also possible to deduce that the chair transition state is a lower energy conformer than the boat transition state, this is true in bother levels of theory and therefore the reaction follows the chair transition state. At higher temperatures, the transition state energy is lower than that of the energy required to reach a transition state at 0k. This is because, at Ok there is no thermal energy and therefore the molecule is closer to the minima.

Nf710 (talk) 16:52, 15 December 2015 (UTC) Looks like you ran out of time here. your energy for the chair TS is 631G is acceptable, however you haven't put your re optimised boat in there. Also you haven't worked out any of the activation energies your self. you have just take the ones from the appendix. you have some decent understanding of the theorey but it would have been better if you could have shown more understanding of the computational methods . furthermore the use of JMols would have been nice.

Nf710 (talk) 16:52, 15 December 2015 (UTC) Only the first section has been marked due to the issue with plagiarism. You can discuss this with mike Bearpark in person.

The Diels Alder Cycloaddition

The Diels–Alder is a [4+2] supraficial cycloaddition between a conjugated diene and a substituted alkene, to form a substituted cyclohexene system. The breaking of pi bonds and formation of two sigma bonds mean that the product is energetically stable and drives the reaction. [11]

[12]

Cis-Butadiene

Optimisation for cis butadiene log file are located here

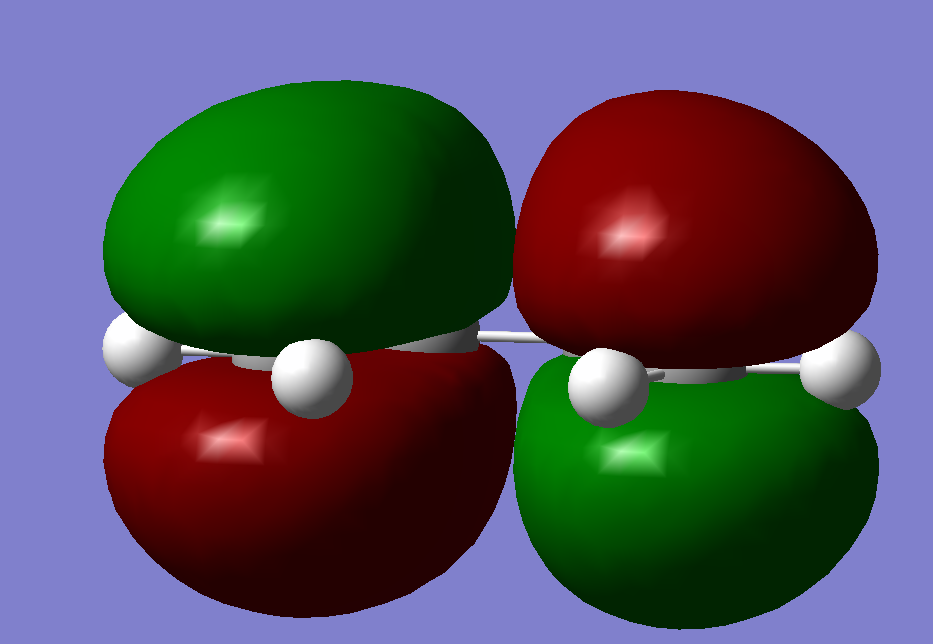
For this optimization, the LUMO and HOMO orbitals are placed below;

Asymmetric with respect to the plane;

Symmetric with respect to the plane LUMO;

Ethylene and transition state optimization

Ethylene was optimized at the same level as the butadiene.

From this result the optimized ethylene and cis butadiene were separated by a distance of less than 2.2 Å or the optimization failed. The C1 symmetry here refers to the lack of symmetry.

An optimization log file of the of the Diels Alder reaction is here

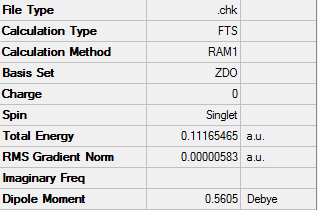
From the frequency analysis we can see that reaction converges towards a maxima stationary point. This is proved to be a transition state due to the 'negative' or imaginary vibration was produced which was at -956.09 cm-1.

Labeling the transition state provides geometric data which is shown below;

In the transition between C5 anad C11 is 2.1192703Å, this is less than double 1.70Å, the van der waals radii, so therefore an interaction exists so the formation of the C-C is favoured.

The reaction pathway is as follows;

For a reaction to occur the HOMO and the LUMO of each reactant need to interact, using this statement. We can analyse the HOMO and LUMO orbitals of the reaction between ethylene and cis-butadiene.

HOMO, antisymmetric with respect to the plane

LUMO, with respect to the plane

From this we can see that the HOMO of the transition state is made up of the HOMO from cis-butadiene and therefore also the LUMO of ethylene, and vice versa for the LUMO of the transition state. This mean that the Diels Alder reaction is allowed.

Cyclohexa-1,3-diene optimisation

Exo Transition State optimisation

After optimizing cyclohexa-1,3-diene and maleic anhydride they were placed 2.1 Å apart in an exo form as seen below. Altering the bridge angle allowed for the optimization to take place.

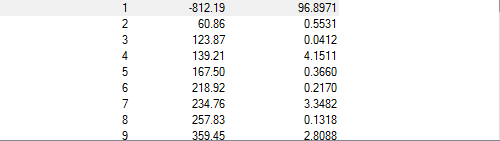
The stationary point is a maximum and found at imaginary 812.19cm-1

LUMO and HOMO visuals are inserted below

HOMO is antisymmetric with respect to the plane

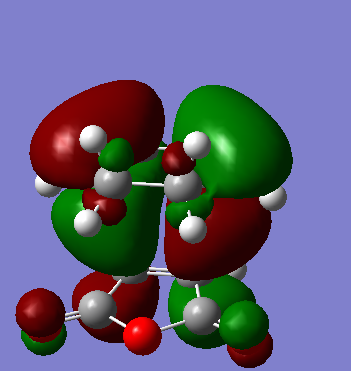
LUMO is antisymmetric with respect to the plane

Endo Transition state optimization

This time the optimized structures were places 2.1Å away from in eachother in an endo formation.

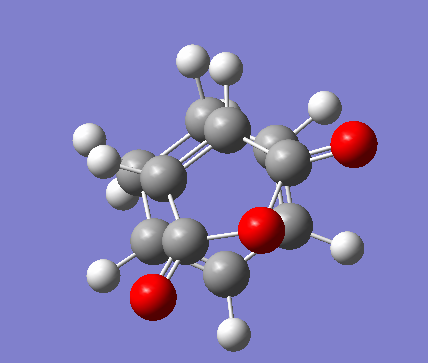
Again the stationary point is found to be at a maxima a negative/imaginary vibration was produced at -806.40 cm-1 the stationary point therefore the transition point.

Orbital Analysis

HOMO Antisymmetric with respect to the plane

LUMO Antisymmetric with respect to the plane

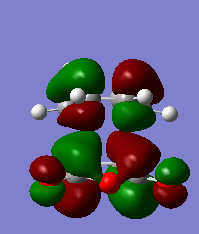
Endo vs Exo transition states

Energies

The endo conformation is of lower energy when optimized at the same level of theory. The reaction conditions will determine which conformer will form the largest proportion of the product

Geometry

By labeling and studying the length of the sigma bonds that are formed, the difference in transition state, either exo or endo, changes the length of the bond formed. The endo transition state has a bond which is shorter than the exo bond when optimized the same. This is due to repulsion between the two fragments in the exo conformer therefore making the bond formed much longer thus removing some of this unfavourable energy. This results in larger ring strain on the maleic anhydride.

Secondary Orbital Overlap

There are secondary orbital interactions which are non bonding in the endo transition state, lowering its energy and making the reaction towards the endo product faster, meaning more kinetically favorable, as it has a lower barrier to entry. The exo-product is the more thermodynamically stable isomer, because it has primary bonding orbital interactions.

It is possible, such as in the Ethylene/Cis-butadiene example, to deconstruct the transition state MO's and obtain the associated reagent orbitals, which can then be used to show whether the reaction can occur. However from looking at the transition state orbitals obtained it is clear that this is not feasible to do (Why not? One may have to look beyond the frotier orbitals though. João (talk) 17:05, 17 February 2015 (UTC)). This does not mean that the reaction does not occur when performed, experimentation has shown the reaction can be carried out. It is more likely that the level of theory that was used is not sufficient enough to produce credible molecular orbitals that follow Frontier Molecular Orbital Theory (Or that the frontier orbital model has its limitations and cannot be applied in this case. João (talk) 17:05, 17 February 2015 (UTC)), and so in order to better probe this the section must be re-performed using a better level of theory, such as B3LYP/6-31G*.

Taking the molecular orbitals of the transition states apart can be used to show if a reaction takes place or not. The level of theory used here is not high enough to produce molecular orbitals that follow frontier molecular orbital theory, however frontier molecular orbital theory also has its limitations for example molecules with many functional groups or electron delocalization, it is common that the HOMO orbital are not strictly localized to a particular site. Also in an aromatic system the HOMO is less likely to react as an nucleophile due to a loss in resonance stability[13]. However there is potential to perform the optimization at a higher level of theory which may improve the results

Conclusion

Throughout this experiment, Diels Alder and the Cope Rearrangement were investigated through the use of transition states in Guassview. Using different methods of optimizing transition states, varying in accuracy, the mechanism in which the reaction proceeded and the conformation of the transition state was able to be found. Transition states were found to be imaginary in frequency at maximum stationary points. From hypothesizing on different conformers energy on the chair transition state, gauche 3 was found to have the lowest energy and therefore the most likely conformer. This was backed up by experimental values given in the appendix, using the B3LYP gave more accurate results than the corresponding HF/3-21G.

The second part of the experiment involved the Diels Alder reaction, taking methods from the Cope Rearrangement it was possible to do a full optimization and frequency analysis on the reaction and this time orbital analysis took place. The orbital analysis made it possible to visualize the HOMO and LUMO orbitals along with their symmetry relationship to the plane, note for Cyclohexa-1,3-diene/Maleic Anhydride cycloaddition this analysis was not able to take place.

To produce more accurate results the Diels-Alder reaction could be done at the B3LYP/6-316 level instead of the less accurate method, this would allow the possibility to compare the results with literature values and maybe even optimize further molecules.