Rep:Modelling MgO RS7913
Introduction
The fact that solid materials vibrate at all temperatures, including 0 K, is an important and useful phenomenon.
In the field of statistical thermodynamics, ‘bulk’ thermodynamic properties of systems or materials such as free energies, heat capacities, expansion coefficients and phase transitions can be calculated from knowledge of the partition function, ‘Q’.[1]

This crudely corresponds to the total number of thermally accessible energy levels in a system, and can be determined via calculation using approximate models, and/or examining the system using various spectroscopic methods.
In a binary crystal such as magnesium oxide, at temperatures below its melting point (3125 K for MgO[2]), there is essentially only population of excited vibrational levels, since population of electronic energy levels above the ground state requires so much energy that this can be considered as negligible. There are no rotations to be considered since we are dealing with an infinite solid lattice. The partition function of the crystal, and therefore thermodynamic properties such as those mentioned above, can thus be reasonably estimated simply by calculation of the vibrational energy levels of the crystal.
Vibrations In Crystals: The Harmonic and Quasi-Harmonic Approximations
In simple crystal structures, vibrations can be modelled using the harmonic approximation.
When modelling infinite systems such as crystals, the harmonic approximation assumes only nearest-neighbour harmonic vibrations, which are small relative to the interatomic separation. The Buckingham potential (a simplification of the Lennard-Jones potential) is used to model the energy of interaction between the Mg2+ and O2- ions that make up the lattice. This can be expanded about the equilibrium bond distance, r0, as follows (Equation 2):
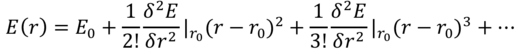
The first two terms of this Taylor series serve as the harmonic potential, and the motion of a one-dimensional monoatomic chain can be modelled as a linear superposition of travelling waves, by applying Newton’s second law of motion as well as the Born-von Kármán periodic boundary condition, which joins the ends of the chain. This ensures each atom has two nearest neighbours, and is appropriate provided the chain is long. This model yields Equation 3, which can be used to calculate the angular frequency, ωk, of a one-dimensional monoatomic chain[3]:
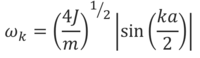
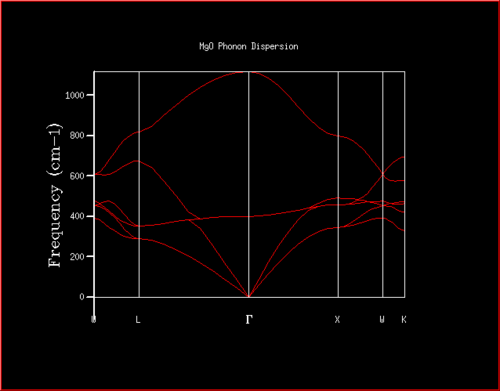
J corresponds to the harmonic force constant (analogous to that in simple harmonic motion), m to the atomic mass, k is the wave vector and a is the interatomic separation. This model can be extended to three dimensions by considering three different wavevectors, kx, ky and kz, for the x-, y-, and z-directions, respectively. All combinations of allowed wavevectors in each of the directions gives rise to all possible vibrations in a 3D crystal, and this also gives rise to degeneracy, i.e. different vibrations having the same energy – degeneracy can be considered by looking at a phonon density of states (Figures 2, 3, 4, 5). Of course, a higher density at a particular frequency (ωk) corresponds to greater degeneracy of vibrations of this energy. A plot of ωk against k, or some reduced wavevector component if considering a three-dimensional system, gives a phonon dispersion, such as that calculated for MgO (Figure 1).
The simple harmonic model can explain a number of features that only depend on the average positions of atoms in a structure and not their motion, often with good accuracy. Calculations are carried out in reciprocal space, by considering a reciprocal lattice vector, a*:
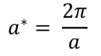
This accounts for the infinite structure that can be made up of repeating unit cells, and a* defines the dimensions of the first Brillouin zone – this is the area over which sampling of phonons is carried out, and is a cube in reciprocal space (k-space).
However, this approximation cannot be used to model the thermal expansion of a crystal since, in this approximation, the equilibrium interatomic distance, r0, is not dependent on temperature. Hence, whilst a number of features that only depend on the average positions of atoms in a structure and not their motion can be explained, such as chemical properties, optical properties and hardness, a static model cannot explain features such as expansion coefficients, heat capacities and conductivity.
The quasi-harmonic approximation introduces the dependence of equilibrium bond distance on temperature and allows for calculations of volume-dependent thermal effects such as expansion coefficients or heat capacities. The approximation assumes that, at each value of the lattice constant (i.e. at each interatomic separation), the harmonic approximation explained earlier holds.
The quasi-harmonic approximation uses the harmonic approximation to calculate vibrations in a crystal, but in addition finds the structure (i.e. interatomic separation) that is of minimum the free energy at the temperature being studied, and this structure is considered as the equilibrium structure. The Helmholtz free energy, being pressure-independent, is calculated using Equation 5[3]:
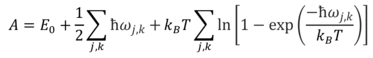
E0 is the internal energy contribution, and the second term is the zero-point energy; these terms can be considered as the ‘U’ term in the ‘A = U – TS’ definition of Helmholtz free energy. The third term is a statistical thermodynamic term that corresponds to the vibrational contribution to the entropy of the system, and can be thought of as the ‘-TS’ term. This term uses the vibrational partition function (Qv) to calculate the entropy.
The harmonic and quasi-harmonic approximations work especially well at lower temperatures since they take into account the zero-point vibrational energy of the system being studied. However, these models do not take into account the intrinsic temperature-dependence of phonon frequencies; the relationship between energy and internuclear separation (for the vibrations) is considered as harmonic i.e. parabolic. Hence, due to neglecting anharmonicity, these models break down at higher temperatures and cannot be used to model phase transitions since the parabolic function does not allow for bond dissociation. The molecular dynamics simulation method works better at higher temperatures, and can sometimes be used to model phase transitions with reasonable accuracy.
Classical Simulation: Molecular Dynamics
Molecular dynamics methods basically simulate the motion of atoms in a real system. These simulations work by taking the ideal structure of a system as the initial configuration, and randomly assigning velocities to all of the atoms such that the overall kinetic energy within the system corresponds to the target temperature being studied. Newton’s second law is then used to calculate the forces on the atoms, and their accelerations. After a certain time dt, known as the timestep, the velocities and positions of the atoms are updated, and this process is repeated until average properties such as the internal energy and temperature of the system settle. At this point, certain properties of the system such as volume and free energy can be deduced. The Buckingham potential is used to model interatomic interactions in the system, being the same as that used in the quasi-harmonic approximation.
Unfortunately, molecular dynamics simulations are considerably more computationally demanding compared to use of the quasi-harmonic approximation, and a compromise must be struck between the size of the system to be simulated, the length of the timestep, and the computational power required to carry out the simulation. Of course, a larger system size and shorter timestep will result in a more realistic and more accurate simulation of a real infinite structure. However, this method does take the anharmonicity of real bonds into account and, as noted earlier, is therefore capable of producing some reasonably accurate results at higher temperature.
Due to the restricted computational power available for this investigation, the ‘Include Shells’ option was not selected, which means a ‘rigid-ion’ model was used. This basically treats the ions as non-deformable, charged spheres, and means that the simulation is not as accurate as ions indeed can of course be deformed to some degree. Also, whilst this method does take anharmonicity into account, it does not account for the zero-point energy of the structure, since it is a classical simulation. Therefore, this method tends to break down at lower temperatures, and cannot be used to model a system at 0 K.
The Coefficient Of Thermal Expansion
As can be seen in Equation 6, the coefficient of thermal expansion is a measure of the rate at which a material expands with respect to temperature, at constant pressure. It is an intrinsic property of a material that is normalised by dividing by the initial volume, V0. The physical origin of thermal expansion stems from the fact that temperature corresponds to the average atomic, or molecular, kinetic energy of a substance. As temperature is increased, more vibrations are excited and the average interatomic spacing will increase due to an increase in the occupancy of excited vibrational states. This can be approached from another angle, by realising that an increase in interatomic separation (i.e. volume) will result in lower frequency vibrations, which is entropically advantageous due to smaller separation between vibrational energy levels leading to an increased population of excited states, and hence an increase in the vibrational partition function, Qv. Since the ‘-TS’ entropic term in the calculation of free energy becomes more influential at higher temperature, it makes sense that an increase in temperature would result in an increase in volume, due to an increase in the entropy of the system being favoured.
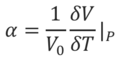
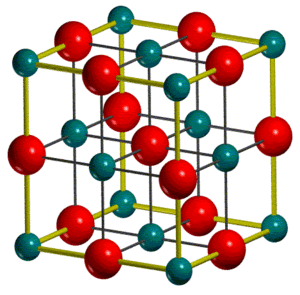
Magnesium Oxide Structure
MgO takes up a face-centred cubic (fcc) crystal structure in the solid state. The conventional unit cell is a cube, containing 4 MgO units, and is most often considered as opposed to the primitive unit cell since it better reflects the symmetry of the lattice.
 |
 |
Experimental
All calculations were carried out using the DLVisualise GUI on a virtual (VMware Workstation on Windows 10) Linux operating system. The GULP (General Utility Lattice Program) code was used to run molecular simulations, and the ‘ionic.lib’ force field was selected for all calculations in the ‘GULP Potential Parameters’ panel, with the ‘Include Shells’ option not selected.
Results & Discussion
Calculation of the phonon modes of MgO
The ‘Phonon Dispersion’ method was run from the execute GULP panel, with Npoints set to 50. This corresponds to the phonons being computed at 50 points in k-space. A 2D view of the resultant plot is shown in Figure 1. In addition, a ‘Phonon DOS’ (density of states) was calculated for a 1x1x1 grid in k-space i.e. a single k-point, and is featured in Figure 2.
 |
 |
Examination of Figure 2, noting the two peaks (acoustic modes) at around 295 and 350, and two more peaks (optical modes) at around 685 and 805 that are half of the intensity, it is clear that the Phonon DOS was calculated for the k-point corresponding to L in the phonon dispersion shown in Figure 1. The fact that the intensity of the optical modes is double that of the acoustic modes indicates that the optical modes are doubly degenerate relative to the acoustic modes. The double degeneracy of the acoustic modes is reflected in the phonon distribution (Figure 2), since each of the dispersion curves that cross L at 295 and 350 cm-1 both branch off into two separate curves to the left of L, whereas the other two curves do not branch off either side of L. By examination of the output ‘Log’ file for the phonon dispersion carried out, one can confirm that the frequencies at point L match the peaks in the phonon DOS, and that this k-point corresponding to the point L is at kx=ky=kz=0.5.
 |
 |

The ‘Phonon DOS’ method was run in the same way as earlier for cubic grid sizes between 2x2x2 and 8x8x8 (Figure 3) inclusive by sequentially increasing the shrinking factors by 1 unit. Densities of states for larger cubic grid sizes were calculated by increasing the shrinking factors in larger steps up until a grid size of 32x32x32 (Figure 4), and a phonon DOS was also calculated for a grid size of 50x50x50 (Figure 5). Increasing the grid size for which the phonon DOS is calculated for resulted in a more accurate DOS being calculated due to a larger number of k-points, i.e. different vibrations, being sampled. The number of k-points the DOS is computed for is equal to the ‘volume’ of the grid, i.e. a 32x32x32 grid size corresponds to 32,768 k-points being sampled. Increasing the grid size resulted in a smoother, more continuous curve, and it was found that a grid size of 8x8x8 gave a continuous curve, however a grid size of 32x32x32 gave a reasonable approximation to the density of states. It can be seen that there is an insignificant difference between the plots of the density of states for the 32x32x32 and 50x50x50 grid sizes, therefore using a 32x32x32 grid size is a reasonable compromise between computational power (i.e. the length of time required to carry out a calculation) and accuracy. The slight increase in accuracy on computing densities of states for larger grid sizes would not be worth the additional time required to carry out the calculation for the setup used in this investigation. Of course, this may not be the case if a very powerful computer were used to carry out the simulations.

| Grid Size | Helmholtz Free Energy / eV | Difference Vs Converged Value |
|---|---|---|
| 1x1x1 | -40.930301 | 0.003818 |
| 2x2x2 | -40.926609 | 0.000126 |
| 3x3x3 | -40.926432 | 0.000051 |
| 4x4x4 | -40.926450 | 0.000033 |
| 5x5x5 | -40.926463 | 0.000020 |
| 6x6x6 | -40.926471 | 0.000012 |
| 7x7x7 | -40.926475 | 0.000008 |
| 8x8x8 | -40.926478 | 0.000005 |
| 12x12x12 | -40.926481 | 0.000002 |
| 16x16x16 | -40.926482 | 0.000001 |
| 22x22x22 | -40.926483 | 0 |
| 32x32x32 | -40.926483 | 0 |
| 100x100x100 | -40.926483 | 0 |
Table 1: Calculated free energy vs grid size.
Increasing the grid size resulted in convergence in the free energy calculated as can be seen in Figure 6 and Table 1. As the grid size was increased from 2x2x2, the free energy calculated decreased until it converged for a grid size of 20x20x20. A larger grid size corresponds to a larger number of k-points being sampled, just as for the phonon densities of states calculated above, and therefore the possibility of calculating a more accurate vibrational partition function, Qv. As explained in the introduction, Equation 5 can be used to calculate the Helmholtz free energy, and a sum over all ‘k’ values is required to calculate the zero-point energy and the vibrational contribution to the free energy of the system. Therefore, the more k-values sampled, the more accurate the calculation. Of course, as k-points corresponding to higher and higher coordinates in k-space (i.e. higher k-values) correspond to phonons of higher energy, their contribution to the free energy of the system becomes less important since population of these higher vibrational levels is less likely. This is why the free energy calculated converges as grid size is increased.
As can be seen in the ‘Difference Vs Converged Value’ column in Table 1, the grid size 2x2x2 would be appropriate for calculations accurate to 1 meV and 0.5 meV, and the 3x3x3 grid size would be appropriate for calculations accurate to 0.1 meV. It is also noted that the free energy calculated converges to -40.926483 eV for a grid size of 22x22x22, with the accuracy of 0.000001 eV being the upper limit for the software used. A further calculation was carried out using a grid size of 100x100x100 to ensure true convergence had been achieved. Even though a grid size of 22x22x22 would in theory be large enough for further calculations of free energy, a grid size of 32x32x32 was chosen to ensure accuracy, since the phonon DOS plot calculated using this grid size also gave a reasonable approximation to the density of states, as can be seen in Figure 4. Calculations carried out using this grid size still took under two minutes, hence this was considered a good compromise between accuracy and time efficiency.
Optimal Grid Size Vs Solid Structure For The Quasi-Harmonic Approximation
The optimal grid size to be used will vary with the solid structure being modelled and, namely, the interatomic spacing in this solid structure. This corresponds to the lattice constant, a, of the structure, which in turn corresponds to the size of the first Bruillon zone in reciprocal space. As noted in the introduction, to calculate phonon densities of states and free energies using the quasi-harmonic approximation, sampling of phonons is done over the first Brillouin zone, which has dimensions of 2p/a. The smaller the lattice constant, a, of the structure, the larger the size of the first Brillouin zone in k-space. Thus, a larger grid size, corresponding to a greater number of phonons sampled within this first Brillouin zone, would be required to gain a reasonable approximation to the DOS and the calculation of accurate free energies. Conversely, for a structure that has a larger lattice constant, a smaller grid size would be sufficient to gain a reasonable approximation to the DOS and the calculation of accurate free energies, and a smaller grid size would therefore be appropriate to ensure computational power is not wasted.
CaO has a fcc crystal structure that is analogous to that of MgO, since Ca is directly below Mg in the periodic table and therefore has very similar properties to Mg. However, Ca2+ does have a slightly larger ionic radius in comparison to Mg2+ due to having an extra shell of electrons, and this results in CaO having a slightly larger lattice constant of 4.80 Å compared to 4.21 Å in the case of MgO. Whilst a slightly smaller grid size would indeed be sufficient to model CaO, this would not spare a great amount of computational power, thus it can be considered that the optimal grid size of 32x32x32 would be appropriate for a calculation on CaO, or another similar oxide.
Zeolites, such as Faujasite, have complex porous structures with much larger interatomic spacings. This corresponds to far larger lattice constants in comparison to an oxide like MgO, and hence a smaller first Brillouin zone in reciprocal space. Therefore, a smaller grid size would be appropriate for a calculation on a Zeolite.
The structure of metals such as lithium can be thought about in terms of the ‘lattice of cations in a sea of delocalised electrons’ picture of metallic bonding, where favourable electrostatic forces of attraction between the cations and electrons hold the structure together. Metals generally take up close-packed structures with the atoms being held very close to one another, giving rise to smaller lattice constants in comparison to an ionic solid like MgO. Therefore, a larger grid size would be appropriate when carrying out calculations on metals, such as lithium, to ensure the accuracy of these calculations.
Modelling The Thermal Expansion Of MgO Using The Quasi-Harmonic and Molecular Dynamics Simulations
All calculations using the quasi-harmonic approximation were carried out using the ‘Optimisation’ function in the ‘Execute GULP’ panel, with ‘Optimise Gibbs free energy’ selected in the ‘Optimisation opts’ panel. In the ‘General opts’ panel, the ‘Phonon DOS’ option was selected, all shrinking factors were set to 32, and calculations were carried out for temperatures between 0 and 2900 K, inclusive, by increasing in 100 K increments. The ‘Final free energy’ and ‘Primitive cell volume’ in the output ‘Log’ files were recorded for each of these calculations.
The variation of free energy against temperature for these calculations carried out using the quasi-harmonic approximation was plotted (Figure 7), and it can of course be seen that the Helmholtz free energy decreases as the temperature is increased. To begin with this decrease follows a curve, however, when the temperature is greater than around 1000 K, this decrease essentially becomes linear. By examination of Equation 5, and comparing this to the standard A = U – TS definition of Helmholtz free energy, it can be seen that the ‘U’ terms consisting of the E0 and the zero-point energy term are temperature-independent, and correspond to the Helmholtz free energy at 0 K, i.e. the y-intercept in Figure 7. The final term that corresponds to ‘-TS’ contains two ‘T’ terms, and has two different kinds of temperature-dependence. The ‘T’ term before the summation would lead to a linear decrease in the Helmholtz free energy with increasing temperature, providing the summation – corresponding to ‘-S’ – is a negative, temperature-independent term. At lower temperatures, the effect of increasing the temperature resulting in an increase in the partition function is significant, and results in the vibrational contribution to the ‘-S’ term (i.e. the summation) becoming more negative as the temperature is increased. As the temperature is increased to over 1000 K, the vibrational contribution to entropy can be considered to be temperature-independent, and the temperature-dependence of the Helmholtz free energy is essentially linear.
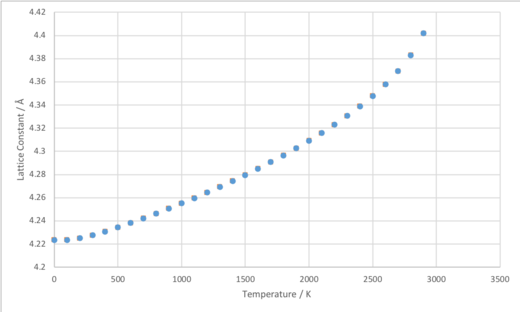
The volumes in the output ‘Log’ files for these calculations carried out correspond to the primitive unit cell. Thus, to calculate the lattice constant, a, these volumes were multiplied by 4 to obtain the volume of the conventional unit cell, and then the cube root was taken to give a. A plot of lattice constant against temperature (Figure 8) shows that, as expected, an increase in temperature results in an increase in lattice constant, i.e. greater interatomic separation.
Molecular dynamics simulations were carried out using a supercell containing 32 MgO units. The ‘Molecular Dynamics’ method was run from the ‘Execute GULP’ panel, with ‘ensemble’ set to ‘NPT’ in the ‘MD Opts’ panel. The ‘Time Step’ was set to 1.0 femtoseconds, ‘Equilibration steps’ and ‘Production steps’ set to 500, and ‘Sampling steps’ and ‘Trajectory write steps’ set to 5. Calculations were carried out for temperatures between 100 and 3000 K, inclusive, by increasing in 100 K increments. The ‘Averaged Cell volume’ for the final timestep, 0.5 ps, in the output ‘Log’ files were recorded for each of these calculations.
The ensemble being set to ‘NPT’ corresponds to the number of particles (N), external pressure (P) and temperature (T) being fixed. Of course, the volume of the system is allowed to vary. It is essential that the correct timestep is chosen, and a compromise must be drawn between computational power and accuracy. The timestep must be long enough to ensure the calculation is efficient, but short enough to ensure all possible vibrations are reasonably well sampled; 10 steps along a given vibration is typically adequate. In this investigation the 1 femtosecond timestep gave reasonable results, and can be deemed acceptable for MgO. In addition, the size of the system to be simulated is important. The supercell used in this investigation, containing 32 MgO units, which also chosen as a compromise between computational power and accuracy of the calculations carried out. The use of a larger supercell would result in greater accuracy, since the increased flexibility would allow for the simulation of a greater number of vibrational modes. Indeed, altering the timestep and size of the supercell could certainly be a subject of further investigation, provided one had the computational resources, or time, required to carry out more complex calcuations involving a shorter timestep and/or larger supercell.

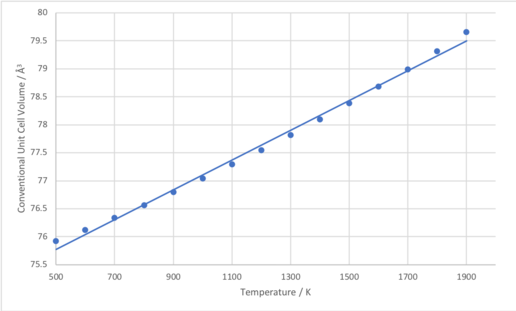
The conventional unit cell volumes calculated – using both the quasi-harmonic and molecular dynamics models – at each of the temperatures studied – are plotted in Figure 9. Equation 6 was used to calculate the coefficient of thermal expansion, where dv/dt was taken as the gradient of the linear
region of the graph. By examination of Figure 9, for the quasi-harmonic approximation, the linear region was taken as the points between 500 K and 1900 K, inclusive, and for the molecular dynamics simulation the points between 100 K and 2100 K, inclusive. The plots of these linear regions and the corresponding linear fits can be seen in figures 10 and 11 for the quasi-harmonic and molecular dynamics simulations, respectively. Calculation of the expansion coefficients gave rise to values of 36.6 x 10-6 K-1 and 29.8 x 10-6 K-1 for the quasi-harmonic approximation and molecular dynamics simulation, respectively. The expansion coefficient does have a considerable temperature dependence, thus the literature values which the calculated expansion coefficients were compared to were averaged over the temperature range being studied, and these values can be seen in Table 2.
| Quasi-Harmonic Approximation | Molecular Dynamics Simulation | |
|---|---|---|
| Temperature range of the linear region / K | 500-1900 | 100-2100 |
| Computed coefficient of thermal expansion / 10-6 K-1 | 36.6 | 29.8 |
| Literature value corresponding to average coefficient of thermal expansion over the temperature range being studied / 10-6 K-1 | 45.3 | 42.3 |
Table 2: Coefficients of thermal expansion for MgO calculated using the quasi-harmonic and molecular dynamics models, and corresponding literature[4] values.
As can be seen in Table 2, the computed values of the coefficient of thermal expansion do agree reasonably well with the literature values, and the quasi-harmonic approximation provides a more accurate value for the temperature range studied. In addition, the expansion coefficient calculated over the temperature range 500-1900 K using the quasi-harmonic approximation was greater than that calculated over the temperature range 100-2100 K, which agrees with the cited literature values.
By examination of Figure 9, it can be seen that the quasi-harmonic approximation best models the system at lower temperatures. As noted in the introduction, this is because the quasi-harmonic approximation takes into account the zero-point vibrational energy of the system. This is neglected by the molecular dynamics model, and results in the model predicting a volume that is excessively small. However, at temperatures above around 2300 K, the quasi-harmonic approximation begins to break down. As the melting point of MgO, 3125 K, is reached, the volume computed using the quasi-harmonic approximation starts to increase at a rapidly steeper and steeper rate. This is because the phonon modes are harmonic, and therefore do not represent the actual motion of the ions at higher temperature, since the population of higher vibrational levels means that anharmonic effects and bond dissociation become important. The quasi-harmonic continues to treat MgO as a fcc lattice even at these higher temperatures, and this ultimately results in an error when attempting calculations for temperatures above 3000 K. It can be seen that, on the other hand, the molecular dynamics simulation does better model the system as the temperature is increased to near to the boiling point of MgO. This model does not neglect anharmonicity, and the atoms are allowed to move apart from one another since they are not restricted by a harmonic potential. As noted in the introduction, the molecular dynamics simulation method can sometimes be used to model phase transitions with reasonable accuracy. However, the molecular dynamics simulations carried out in this investigation do start to break down at temperatures above roughly 2500 K, where the cell volume calculated starts to hover up and down. This is because the timestep of 1.0 femtoseconds used was not short enough to model the motion of atoms accurately at these higher temperatures, due to the greater kinetic energy the particles have. This could in theory be resolved by using a shorter timestep and, as mentioned in the introduction, the molecular dynamics simulation method can sometimes be used to model phase transitions with reasonable accuracy. Using a shorter timestep for these calculations could be a subject for further research.
Conclusion
An investigation was carried out to compare the quasi-harmonic approximation and molecular dynamics model in approximating the thermal expansion of magnesium oxide. To begin with, it was discovered that the optimal grid size to use for quasi-harmonic calculations in this investigation was 32x32x32, since this grid size gave rise to a sufficiently realistic phonon DOS as well as convergence of the Helmholtz free energy calculated to the maximum level of precision possible using the GULP program used. This grid size was used for all subsequent calculations.
The quasi-harmonic approximation was used to calculate the Helmholtz free energy of MgO at temperatures between 0 K and 2900 K, inclusive, and it was found that an increase in temperature resulted in a decrease in the free energy.
Finally, the thermal expansion of MgO was modelled using both the simple harmonic approximation and a molecular dynamics simulation over a temperature range of 0 K and 3000 K. It was found that the quasi-harmonic approximation was good at modelling MgO at low temperatures since it takes the zero-point vibrational energy of the system into account. However, the approximation broke down at higher temperatures since it does not take anharmonic effects into account, a calculation at 3000 K resulted in an error output file. The molecular dynamics method did not model MgO well at lower temperatures since this approximation does not take the zero-point vibrational energy of the system into account, and thus a calculation at 0 K resulted in an error output file. It did fare better than the quasi-harmonic approximation at higher temperatures, however the molecular dynamics model did start to break down at temperatures approaching 3000 K. This is likely to be due to the 1.0 femtosecond timestep used not being sufficiently short to model the motion of atoms with such high kinetic energies. The coefficient of thermal expansion of MgO was calculated using the quasi-harmonic and molecular dynamics models, over the temperature range 500-1900 K and 100-2100 K, respectively. This yielded values of 36.6 x 10-6 K-1 and 29.8 x 10-6 K-1 for the quasi-harmonic and molecular dynamics approximations, which correlate reasonably well with literature values[4] of 45.3 x 10-6 K-1 and 42.3 x 10-6 K-1 for the corresponding temperature ranges. Discrepancy in the results in comparison to the literature could in theory be minimised by using a larger grid size and including shell modes in the quasi-harmonic model, and by using a larger supercell and shorter timestep for molecular dynamics simulations. To determine whether this is indeed the case could be the subject of further investigation. However, one must not forget that these computational models provide a convenient and fast way of calculating thermodynamic properties such as free energy and volume without having to carry out experiments on the systems in reality, in the laboratory. Trying to gain more accurate results using computational methods will certainly require more computational power, and this requirement may finally begin to take away from some of the advantages of using a computational method.
References
-
- ↑ P. Atkins and J. De Paula, Atkins' Physical Chemistry, OUP, 2014.
- ↑ W. M. Haynes, CRC Handbook of Chemistry and Physics, CRC Press, Boca Raton FL, 2011.
- ↑ 3.0 3.1 M. T. Dove, Introduction to Lattice Dynamics, Cambridge University Press, 1993.
- ↑ 4.0 4.1 O. L. Anderson and K. Zou, J. Phys. Chem. Ref. Data, 1990, 19, 69-81.