Rep:Mod 3:MaJfnif05

Cope Rearrangement

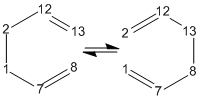
Thermally, 1,5-hexadiene undergoes a [3,3]-sigmatropic reaction or Cope rearrangement

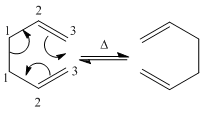
. (Known as the Cope rearrangement because it involves only carbons. It is called a Claisen rearrangement when one oxygen atom is present). This is accepted to be a concerted migration; there are no intermediates in the reaction profile. Pericyclic reactions proceed via cyclic transition states. This reaction involving 6 (4n+2) electrons is allowed via Huckel topology with suprafacial components. Two reasonable transition states are the “boat” and “chair”

.

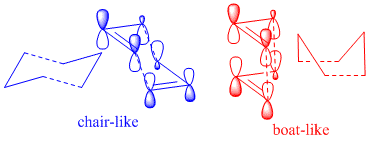
Optimising the reactants and Products

1,5-hexadiene was drawn in gaussview using the R-group fragments; n-butyl and 2 vinyl fragements(the n-butyl fragment had to be drawn first in order for the number of hydrogen atoms on the C atoms to be correct). All of the dihedral angles where then set to 180° (including the H-C-C-C angle). The structure was then cleaned and an optimisation calculation carried out using the Hartree-Fock method and 3-21G basis set. The total energy of the resulting structure was -231.69254 Hartree (table 1). After symmetrisation, the point group was found to C_i, indicating a centre of inversion in the molecule.This correlates to the anti2 conformer. If only the central 4 carbon atoms are set to 180°, antiperiplanar conformation (app) then the resulting HF/3-21G optimised structure correlates to anti1 . This is slightly lower in energy than anti2 by about 0.04 kcal/mol. Equally, if central dihedral angle is 180° and the both outer C-C-C-C dihehral angles are set to 0° or synperiplanar (spp) then the optimised structure now has a plane of symmetry, σ_h and corresponds to anti3. Finally, if only 1 of these out dihedrals is set to 0°, then the resulting structure is anti 4. It follows that anti3 with more unfavourable near spp interactions is higher in energy than anti4. It is worth noteing that it is important to first clean the structure before optimising otherwise, a different energy and therefore, slightly different conformation results. For example, in trying to get anti3 but forgetting to press clean gave a conformer of total energy -231.68540 Hartree, with C_2h symmetry; an energy difference of about 2.3 kcal/mol.

Setting the dihedral angle of the central 4 carbon atoms to a gauche (60°) conformation, cleaning and then optimising to the same level of as previously done gives gauche3 with a total energy about 0.04 kcal/mol lower than the corresponding anti1. This isn’t a significant different considering the barrier to rotation about something like ethane is around 3 kcal/mol. Staggered conformations should be lower in energy eclipsed because they avoid unfavourable eclipsing interactions. (On a plot of energy against dihedral angle, staggered conformations would be expected to form the energy minima and eclipsed energy maxima). On the staggered conformations, the app conformer would be expected to be lowest in energy as it places the two largest groups as far away as possible whereas the gauche conformer puts them closer together.

Table 1.Summary of conformers computed

Structure	Total Energy/Hartree HF/3-21G	Point Group	Assigned Conformer	Relative Energy/ Kcal/mol
	-231.69254	Ci	Anti2	0.08
	-231.69260	C2	Anti1	0.04
	-231.68907	C2h	Anti3	2.25
	-231.69097	C1	Anti4	1.06
	-231.69266	C1	gauche3	0.00

Reoptimising the anti2 conformer to the higher level of theory; B3LYP/6-31G* results in a different total (electronic) energy;-234.61170 Hartree. The point group is still C_i. There are some slight differences in bond lengths and dihedral angles (table 2). The largest difference is in the outer C-C-C-C angle.

Table 2. Comparison of bond lengths and angles between the two levels of theory. Bond lengths are in Å and angles in °

Angle or bond length	HF/3-21G	B3LYP/6-31G*
C=C	1.32	1.33
C-C(all 3 same)	1.51	1.50
Centre 4: C-C-C-C	180.0	180.0
Outer C-C-C-C	114.7 (-114.7)	118.5 (-118.5)
H-C-C-C	-1.09 (1.094)/ 179.1 (-179.1)	-0.71 (0.71)/179.6 (-179.6)

A frequency calculation was carried out (with the same higher level theory). This confirmed that the structure was a true minimum, there were no negative frequencies. This calculation also allows the potential energy to be corrected in order to be able to compare energies with experiment.

Table 3. Computed Energies for Anti2 at B3LYP/6-31G* level

Energy Term	Value/Hartree
Electronic Energy	-234.61170
Sum of electronic & zero point energie at 0K	-234.469203
Sum of electronic & thermal energies at 298.15 K	-234.461857
Sum of electronic & thermal free energies	-234.500776

Optimising the “chair” and “boat” Transition State

The allyl fragment was draw in gaussview such that the C-C bonds had a bond order of effectively 1.5. This was then optimised to the HF/3-21G level. Two of these optimised fragments where then used to make a guess at the chair transition state. The distance between the terminal C's of the two fragments was 2.21 Å (close to 2.2). This guess was then optimisation separately in two different ways (using two methods). The first way involves computing the force constant matrix (Hessian) in the first step of the optimization. The structure was optimised to a transition state (berny) with the key words opt=noeigen at the HF/3-21 G level. A negative frequency of 818 cm^-1 was obtained. The animated vibration is illustrated

Chair TS vibration at -818cm^-1

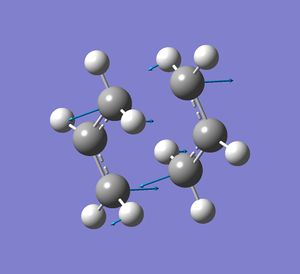
. The resulting difference between the two terminal carbons was 2.02 Å and the C-C bond length was 1.39 Å. The allyl fragments were no planar as in the guessed structure. The second method was the frozen coordinate method. The distances between the two terminal carbons of the fragments were set to 2.2 Å (these are the bonds that are forming and breaking during the Cope rearrangement). The structure was then optimised at the same level of theory to that done previously. These fixed bond lengths were then optimised using a transition state optimisation . The resulting bond forming/bond breaking lengths were 2.02 Å, the same as that found previously. The resulting point group of the molecule was C_2h. The boat transition structure was optimised using the QST2 method. The transition state is found by interpolation between the reactant and product 1,5-hexadienes. The HF/3-21G optimised anti2 1,5-hexadiene structure was used for both the reactant and product geometries. The numbering of the product was changed relative to the reactant so that it corresponded to the reactant after having undergone a Cope rearrangement. The numbering change required for my molecule is shown. The numbering of the hydrogen atoms also had to be changed. The best way of doing this was found to be working out where atom 1 should be in the product and changing it manually, then atom 2, then atom 3 and so on.

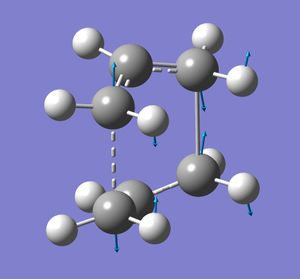
The dihedral angle of the 4 central carbons had to be changed to 0° and both inside C-C-C angles had to be changed to 100° in both the reactant and product molecules. The calculation gave a boat-like transition structure of energy -231.60280 Hartree. Interestingly gaussview added a single bond between one end on the two fragments. The imaginary frequency was at -839 cm^-1 . The vibration is shown. The distance between the terminal c-c bonds is 2.14 Å and the C-C bond length is 1.38 Å.The point group was found to be C2v.

boat TS vibration 839 cm^-1

The intrinsic reaction coordinate (IRC) was then used to follow the minium energy path from the chair transition state down to the product on the potential energy surface. The HF/3-21G optimised chair transition state was used and initially the IRC was run with 50 points in the forward direction with the force constants calculated once. When this failed, the final structure was minimised. Then the IRC was rerun but with the force constants computed at every step. There were still 50 points. A third option was the run the IRC with more points. These calculations each took between 15 and 30 minutes.

The chair and boat transition were reoptimised at the B3LYP/6-31G(d) level and frequency calculations carried out on both. The geometries and energies obtained from this level of theory and the previous are summarised in table 4.

Table 4.Geometries and Energies from different levels of theory

Parameter	Boat HF/3-21G	Boat B3LYP/6-31G*	Boat HF/3-21G	Boat B3LYP/6-31G*
Bond breaking/forming C-C/Å	2.14	2.21	2.02	1.97
Fragment C-C/Å	1.38	1.39	1.39	1.41
Electronic Energy/Hartree	-231.60280	-234.54309	-231.61932	-234.55698

The geometries are very similiar but the energies are quite different between the two levels of theory.

The activation energies at 0 and 298.15 K can be calculated for the reaction via the boat or chair transition state. This is done by taking the difference between the electronic and zero point energy between anti2 and the transition state. This has been done for the B3LYP/6-31G(d) values.

Table 5.Activation Energies B3LYP/6-31G*

TS	sum of electronic & zero energy at 0K/Hartree	sum of electronic & zero energy at 298.15K/Hartree	activation Energy at 0K kcal/mol	activation Energy at 298.15 K/kcal/mol	Exp. O K kcal/mol
chair	-234.414919	-234.408998	31.06	33.17	33.5 +_0.5
boat	-234.402340	-234.396006	41.96	41.32	44.7 ± 2.0

The values are in reasonably agreement with experiment. The activation energy for the boat transition state is higher than for chair indicating the Diels Alder reaction proceeds via a chair transition state.

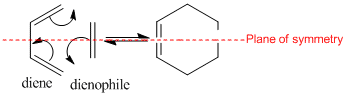
Diels Alder Cycloaddition

A cycloaddition is a pericyclic reaction involving the formation of two or more σ sigma bonds between the ends of two or more conjugated π systems via a concerted cyclic transition state. A Diels Alder reaction is a particular type of cycloaddition involving a diene and dienophile . There are several ways of explaining which reactions are allowed or forbidden. For example, the frontier orbital theory and the conversation of orbital symmetry. Orbital correlation diagrams can also be drawn. There is also transition aromaticity. The reactions can be normal electron demand or inverse electron demand. Normal electron demand involves the interaction of rich diene with the LUMO of an electron deficient dienophile. Inverse electron demand involves the reaction between an electron deficient diene and electron rich dienophile and is usual when a hetero-diene is involved .

Butadiene and ethane

This is a π₄s +π₂s Diels Alder reaction, which thermodynamically is expected to go towards forward of the cyclohexadiene ring as two π bonds in the reactants are being replaced by only 1π bond in the product.

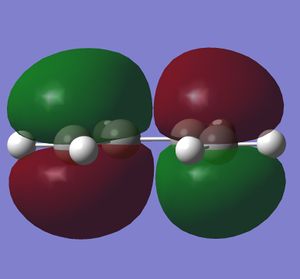
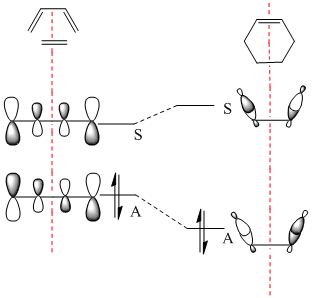
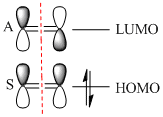
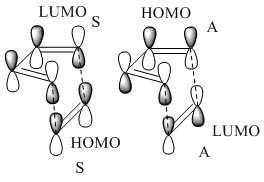
Butadiene was optimised to the semi-empirical/ AMI level of theory and the MOs computed. The HOMO with1 node (in addition to a nodal plane) is antisymmetric (A) with respect to the plane of symmetry bisecting the central C-C bond. The LUMO with 2 nodes is symmetric (S) with respect to this plane. The HOMO and LUMO of ethene (from LCAO) show that the HOMO is symmetric with respect to this plane of symmetry and the LUMO antisymmetric. Hence the HOMO of butadiene could interact with the LUMO of ethene or vice versa. The reaction is allowed, the signs of the orbitals match up. An orbital correlation diagram could be constructed form the reactants to products. Orbitals of the same symmetry (A or S) are joined up. (part of this has been constructed). . It is the HOMO of the butadiene that reacts with the LUMO of ethene.

HOMO of butadiene

LUMO of butadiene

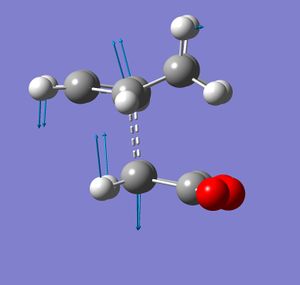
In gaussview, 2,2,2-bicyclooctane was draw and a C=C bond added and the number of hydrogen atoms adjusted. This structure was then optimised at the semi-empirical/AMI level. The bridging -CH2CH2- fragment was then removed and replace with hydrogen atoms. The C-H bond length of these additions were adjusted to equal the other C-H bond lengths. The terminal bond lengths between the ethane component and the butadiene were then frozen at 2.2 Å and an optimisation to a minimum was run at the same level of theory as done previously. This is the frozen coordinate method. A transition state optimisation was then set up differentiating along these coordinates using a normal guess Hessian. The resulting structure had one negative or imaginary frequency indicating that it is a transition state. The vibration corresponding to this is shown. The transition state structure resembles the reactants indicating an early transition state.

TS vibration

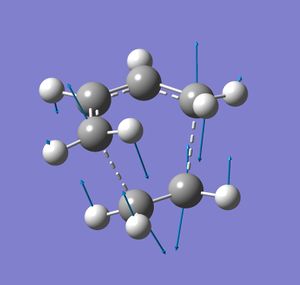
The vibration shows that as the (what was) ethene component moves towards the ends of what was the butadiene reactant, what where the double bonds of butadiene appear to lengthen and what was the sigma bond appears to shorten. The C-C bond length in the ethene component is 1.38 Å, which is longer (implying that it is weaker) than the 1.33 Å of C=C in ethene itself . The C=C bond length butadiene itself is reported as 1.34 Å but a longer bond length of 1.38 Å is found for corresponding bond in the transition state. The bond corresponding to the σ bond in butadiene is also found to be shorter by about 0.04 Å. This also corresponds to the two new σ bonds forming between the two components, the breaking of the π-bonds and the formation of a new one. Both new σ bonds also appear to be forming at the simultaneously implying that this a synchronous concerted mechanism. These bond lengths in the transition state are both the same length at about 2.2 Å.

The ethene approaches from below the plane of the butadiene. The transition state is suprafacial in both components, that is both new σ bonds are forming to the bottom face of butadiene and both are forming to the top face of the ethene component. This suprafacial or Huckel transition state associated with a plane of symmetry is aromatic as it involves 6 cyclically conjugated π electrons (4n+2). This is a thermally allowed reaction. The angle of approach of the ethene component with respect to the butadiene is approximately 111° at the B3LYP/6-31G*level of theory. This correlates approximately with a tetrahedral angle of approach. An angle of approach of approximately 90° might be expected to give maximum orbital overlap but maybe this angle is a compromise between this a steric repulsion. The planar, geminal hydrogen atoms of the ethene reactant are also distorted towards a tetrahedral angle of 106° in the transition state at this higher level of theory.

One of the lowest positive frequencies appears to show one of the σ bonds forming slightly before the other, asynchronous. Other higher level computation calculations within the literature seem to support the conclusion here that in the case of butadiene and ethylene the reaction is synchronous. Substituted of one of the hydrogen atoms on ethylene by an electron withdrawing group may be expected to lead to asynchronous concerted mechanisms.

The relative energies of the frontier molecular orbitals control the reactivity . The smaller the energy difference between the HOMO of butadiene and the LUMO of ethene, the greater the stabilisation of the resulting orbitals and also the faster the reaction. Kinetically, this reaction is expected to be slow. Experimentally, this is found to be the case, at 165°C and 900 atm the reaction takes 17 hours to give a 78 % yield . The HOMO and LUMO are not that close in energy. This is due to the electronics of the reactants. The energies will be closer and the reaction faster if the dienophile is electron deficient and the diene electron rich. This is normal electron demand. Adding an electron donating substituent to the diene lowers the energy of the HOMO. Adding an electron withdrawing group to the dienophile increases the energy of LUMO. This brings the two closer in energy (as the HOMO is higher in energy than the LUMO.)

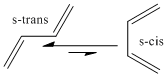
The butadiene has to be in the s-cis conformation to react in the Diels Alder however the s-trans conformation is expected to be lower in energy due to sterics. Computational the s-trans conformer was found to be about 1 kcal/mol lower in total energy than the s-cis at the semi-empirical/AMI low level of theory. Hence there is an additional activation energy required to go from s-trans to s-cis.

Cyclohexa-1,3-diene and Maleic Anhydride

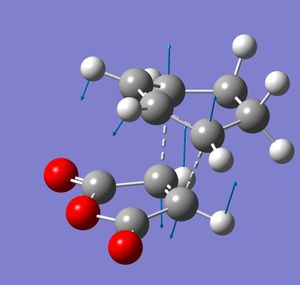
This reaction is still a [4+2] Diels Alder but the conformation of the diene is now fixed to be s-cis by the ring and the dienophile is now electron deficient. There is also now an additional consideration, the LUMO of maleic anhydride could approach the HOMO of cyclohexane in an endo or exo fashion. This is an issue of regioselectivity. The reaction is under kinetic control, giving the endo adduct as the major isomer and the exo as the minor product. This is known as Alder’s endo rule.

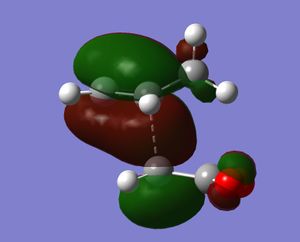
Both transition states were optimised using the freeze coordinate method at the semi-empirical/AMI level. Each gave one negative frequency, -806 cm^-1 for the endo transition state and - 812 cm^-1 for the exo. These vibrations are illustration. As for the above reaction, they show the various bonds breaking and forming. At this level of theory, the exo TS was found to be 0.68 kcal/mol higher in energy than the endo TS. This agrees with the endo isomer being the kinetic product of the reaction. Both TS were then optimised to the B3LYP/3-21G level. At this level of theory, the endo isomer was 1.04 kcal/mol lower in energy than the endo TS. This is a larger energy difference than previously. This can be explained by computing the HOMO for each transition state. In the endo isomer there is an additional bonding interaction between the π-bond forming at the back of the diene and the carbonyl carbons. These secondary orbital effects cannot be present in the exo TS.

Exo vibration

Endo vibration

Exo HOMO

Endo HOMO

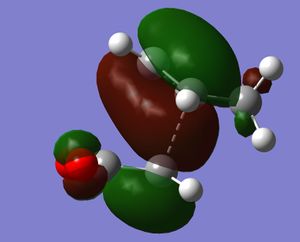Both the endo and exo products were optimised to the AMI level of theory. The endo isomer was found to be lower in energy by about 1.8 kcal/mol.The exo isomer may be more strained due to steric repulsion between the maleic anydide component and the -CH2CH2- fragment.This implies that the endo product is also the favoured thermodynamically as well as kinetically. Thermodynamics is governed by the stability of the product and the kinetics by the TS.This is only a low level of theory though.This should be verified at a higher level.

There doesn't seem to be any difference between the endo and exo TS with respect to the various parameters listed in table 6. The transition states should be optimised to a higher level.

Table 6. Comparision of Endo and Exo*

TS	σ bonds forming	π bonds breaking in cyclohexaene	π bond forming	π bond breaking in MA	through space OC-O-CO
endo	1.56	1.52	1.33	1.54	2.34
exo	1.57	1.52	1.34	1.54	2.34

Comparision of Comp. Techniques.

Molecular mechanics is a classical approach and cannot deal with secondary orbital interations, which are quantum mechanical. The above methods are based on quantum mechanisms and thus can be take this into account.

References

1 Hartree=627.509 Kcalmol^-1

Click