Rep:Mod 1: Tom Campling

Analysis of Vibrational Frequencies

The aim of the section was to calculate the vibrational frequencies of the C=C and C-Cl bond stretches in molecule 12 and its dihydro derivative. In order to do this, a different method is needed. The Gaussian B3LYP/6-31G(d,p) method was employed after the prior optimizations with MM2 followed by RM1. This method can take a long time and it is beneficial to submit the calculations to a more powerful computing interface.

The table below shows the vibrations of 12 and their associated frequencies found using the Gaussian method mentioned above.

Key Vibrations of Molecule 12

Interaction	Frequency (cm-1)	Vibration	Frequency From Literature (cm-1)
C-Cl Stretch	771		600 - 800
(anti) C=C Stretch	1737		1620 - 1680
(syn) C=C Stretch	1757		1620 - 1680

The frequencies of the two alkene bonds differ by 20 cm^-1. The anti C=C bond has the lower frequency of the two bonds and is therefore the weaker bond with a higher energy. This is indicative of its higher reactivity and is further reason for the formation of the product discussed below.

Upon comparison with the literature values, the C-Cl stretch is in the range quoted. The values obtained for the C=C stretch however are a lot higher than the literature values.

The table below shows the vibrations of the dihydro derivative of 12 and their associated frequencies found using the Gaussian method mentioned previously.

Key Vibrations of the Dihydro Derivative of 12

Interaction	Frequency (cm-1)	Vibration	Frequency From Literature (cm-1)
(syn) C=C Stretch	1758		1620 - 1680
C-Cl Stretch	774		600 - 800

The frequencies of the C-Cl bond in the dihydro derivative is higher indicating a stronger bond. A stronger bond results from the removal of secondary orbital interactions - the donation of electron density to the C-Cl antibonding orbital from the pi bond anti to the chlorine that is present in 12 but not here.

The frequency of the alkene bond in the dihydro derivative is almost exactly the same as in molecule 12 (higher by 1 cm^-1). This indicates there is little increase in strain in the remaining double bond caused by the newly sp³ hybridised carbons on the adjascent ring system. It also indicates that this alkene bond plays little part in secondary orbital interactions that take place between the other alkene bond and the antibonding orbital of the C-Cl bond.

Mini Project

Comparison of the Two Geometrical Isomers of 2-Fluorovinyl Benzene.

The aim of this mini project is to confirm the assignment of two fluorine containing isomers found in the literature. The isomers were differentiated in the literature by the size of the coupling constants found in the NMR spectra. These values were then compared with known values for coupling constants and conclusions were drawn about which isomer is which. The values that are being used for comparison however are most likely to be from molecules that don't contain fluorine atoms. Fluorine is the most electronegative element in the periodic table and so can exert a strong electron withdrawing effect on neighbouring and nearby atoms; thus affecting the electron density surrounding the nearby nuclei and so potentially affecting NMR readings. This project aims to confirm or contest the assignments of the two geometrical isomers shown below and also discover whether or not the computational model is suitable for such an experiment.

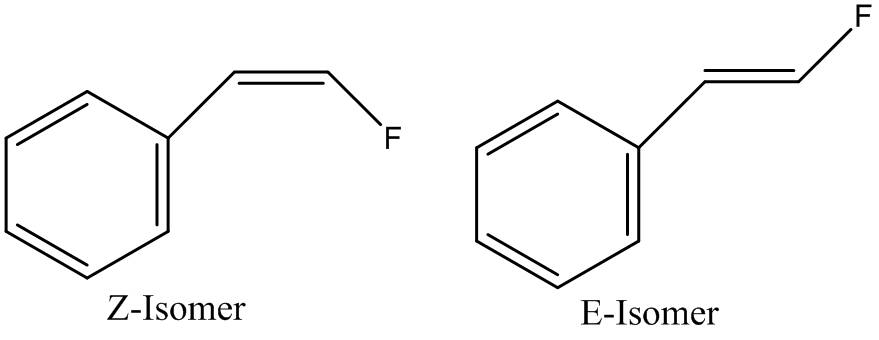
The two isomers were drawn in ChemBio 3D and optimised using the MM2 force field. They were then submitted to the SCAN service to perform a Gaussian B3LYP/6-31G(d,p) optimization. The optimized structures calculated can be seen by clicking the buttons below:

These structures were then resubmitted to the SCAN interface in order to find the NMR spectra of the two molecules. The data received for each calculation are presented in the table below

The ¹³C NMR shifts calculated are compared with the shifts found in the literature in the two graphs shown below.

The graphs show that the literature and computational method match up very well and is a strong indication into suggesting that the correct isomer has been assigned. In order for further confirmation, an inquiry into the J coupling constants was carried out. Janocchio was used to calculate the coupling constants of the geometrically optimized molecules.

J_H-H across the double bond for the E isomer was calculated as 8.22 Hz (literature J_H-H 10 Hz)

J_H-H across the double bond for the Z isomer was calculated as 8.22 Hz (literature J_H-H 5 Hz )

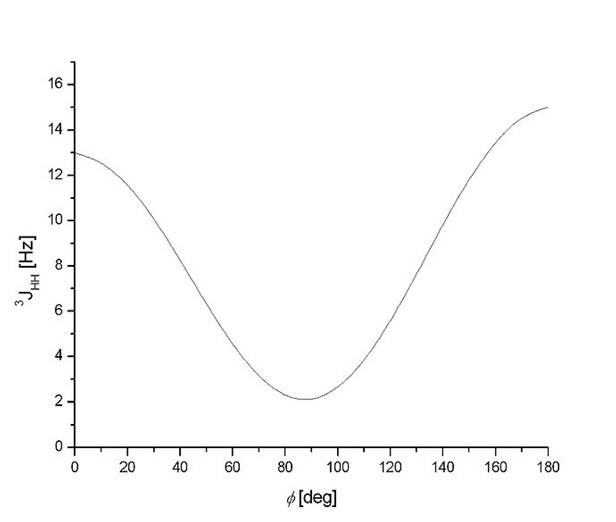
The J coupling constants found are identical for both isomers. This can be explained by appreciating the fact that the isomers are planar throughout the molecule and therefore the dihedral angle between the two protons either of the alkene bond for the cis and trans isomer is 0^o and 180^o respectively. Investigation of the Karplus curve (shown below) shows that the coupling constant expected for these two angles are expected to be similar but not identical. The results obtained indicate that it does not calculate coupling to other elements (for example coupling to the fluorine atom cannot be calculated), or take into account the presence of other elements in the vacinity. This suggests that the Janocchio software cannot be applied for this application.