Rep:Mod 1: Celeste van den Bosch

Instructions: Module 1

See also: CvdB Mod:2, CvdB Mod:3

Modelling using Molecular Mechanics

For this investigation, molecular mechanics are introduced by looking at the hydrogenation of a cyclopentadiene dimer as well as the stereochemistry and reactivit of an intermediate of Taxol. For these two case-studies the Allinger force field MM2 and MMFF94 will be used, the latter of which is useful for modeling biological systems. These two force fields can be used to minimize the energy of molecules based on experimental data for factors such as bond length, steric effects and van der Waals contributions.

Hydrogenation of Cyclopentadiene Dimer

Cyclopentadiene can dimerise via a Diels-Alder reaction to two stereo-isomers; exo and endo, dicyclopentadiene.

Endo Product Bonding Interactions Diagram

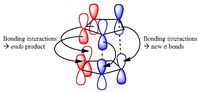
The exo product (1) is more stable and is formed in a reversible reaction under thermodynamic conditions, however the endo product (2) dominates in irreversible reactions and is the kinetic product which cyclopentadiene dimerises to specifically produce. Using an Allinger MM2 force field, the endo and exo structures were optimised to achieve minimum energy with the results of the calculations summarized in Table 1. As the program used is based on known molecules, the thermodynamic product is expected to have the lowest energy as it is the more stable product and from these results this is observed: the exo product is thermodynamic product because its total energy is lower than that of the endo product. As part of a pericyclic reaction, the specific preference for the endo form can be rationalised based on molecular wavefunctions which show that the stability of the transition state favours the formation of the endo product (see diagram right) however calculations which would take the orbitals into account go beyond the scope of the MM2 force field.

Table 1 - Summary of results for the two stereo-isomers of cyclopentadiene dimer

Dimer	1	2	% Difference
Isomer	Exo	Endo
Control	Thermodynamic	Kinetic
Image	Exo Dimer	Endo Dimer
3D Visualisation	File:M1 - Cyclopentadiene Dimer Exo 1.cml	File:M1 - Cyclopentadiene Dimer Endo 2.cml
Total Energy (kcal mol-1)	31.8765	33.9975
Total Energy (kJ mol-1)	133.37	142.25	6%
Stretch	1.2850	1.2509	(-)3%
Bend	20.5783	20.8477	1%
Stretch-Bend	-0.8382	-0.8358	0%
Torsion	7.6559	9.5108	22%
Non-1,4 van der Waals	-1.4167	-1.5435	9%
1,4 van der Waals	4.2346	4.3198	2%
Dipole/Dipole	0.3775	0.4476	17%

As these results for the two molecules were generated using the same force field it is possible to compare them relative to each other, therefore the percentage difference has been calculated. From these results it can be seen that the total energy suggests that 1 is the thermodynamic product of the dimerisation as it's energy is relatively lower, by 6%, compared to 2. This lower energy has been calculated because overall the exo form,1, deviates less from normality than the endo form,2, for all the areas of analysis apart from stretching. The greatest difference between the two products are the torsion and dipole/dipole contributions with percentage differences of 22% and 17%, respectively. As the endo form is more folded (in on itself), it follows that it will have a higher torsion due to steric effects than the exo form which is "flatter" and therefore less likely to suffer from torsion. In the MM2 force field are used to represent electrostatic contributions and again due to the greater steric effects which the product endo form has, 2 was calculated to have a higher total energy.

Additionally the hydrogenation of the dimer was considered and data pertaining to two hydrogenated products has been summarized in Table 2.

Table 2 - Summary of results for the hydrogenation of a cyclopentadiene dimer

Compound	3	4	% Difference
Image	Hydrogenated Endo	Hydrogenated Endo
3D Visualisation	File:M1 - Cyclopentadiene Dimer Endo 3.cml	File:M1 - Cyclopentadiene Dimer Endo 4.cml
Total Energy (kcal mol-1)	35.6850	31.152
Total Energy (kJ mol-1)	149.31	130.34	14%
Stretch	1.2778	1.0959	15%
Bend	19.8588	14.5261	31%
Stretch-Bend	-0.8344	-0.5494	41%
Torsion	10.8117	12.4971	(-)14%
Non-1,4 van der Waals	-1.2237	-1.0709	13%
1,4 van der Waals	5.6326	4.5125	22%
Dipole/Dipole	0.1621	0.1406	14%

Full reaction scheme for the hydrogenation of dicyclopentadiene

Apart from torsion, product 4 deviates less from normality than product 3, cumulating in a lower total energy suggesting that 4 is the thermodynamically favoured product. From literature , it can be seen that in this case the thermodynamic product is also the first step in the hydrogenation of dicyclopentadiene and that the bond which hydrogen has been added across in 4 has been shown to proceed five times fast than the hydrogenation of the other double bond. Therefore the full reaction proceeds as per the reaction scheme right. Further, it can be noted that despite both hydrogenated products being formed from the endo dicyclopentadiene structure, 2, these two products have greater percentage differences. The greatest of these are due to the stretch-bend and bend only contributions. This is likely due to the difference between having all unsaturated bonds in either a five or six membered ring. It can be suggested that having an unsaturated six-membered ring is more favourable as it can adopt the lower energy chair conformation.

In conclusion, it has been determined that the thermodynamic product of the Diels-Alder formation of dicyclopentadiene has a lower total energy however the kinetic product is the main product and its formation can only be understood in terms of molecular wavefunctions. In the hydrogenation of this dicyclopentadiene it was determined using molecular mechanics that the reaction is under thermodynamic control. This investigation could be taken a step further with one modification being the use of different force fields to demonstrate the effect of orbital overlap in the transition state which stabilises the endo form.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

In the synthesis of Taxol (as proposed by Paquette), one of the key intermediates is the molecule below (carbonyl pointing either up, 9 or down, 10):

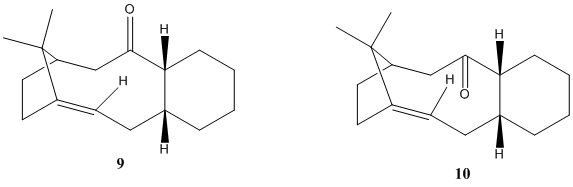
As these two molecules are atropisomers of each other, ChemBio 3D was used to investigated which of the two structures is the most stable. An MM2 force-field was used to determine the lowest energy between the two isomers. The data for these two appeared very similar at first, however it was noted that 9 had the six membered rind in a chair conformation while 10 was in a twist boat conformation. From these values it appeared that having the carbonyl down was the more stable of the two as the total energy was lower for this isomer. This did lead to manual editing of the structure in order to find the chair of the isomer with the down carbonyl which ultimately appears to be the lowest geometry for this intermediate. The MM2 data for the three structures are summarized in Table 3:

Table 3 - Various Taxol Intermediate Geometries

Atropisomer	9 - Carbonyl Up	10 - Carbonyl Down	10 - Carbonyl Down
Geometry of 6-membered ring	Chair	Twist Boat	Chair
Jmol
MMFF94 Total Energy (kcal mol-1)	70.54	66.35	60.56
MM2 Total Energy (kcal mol-1)	47.84	46.43	42.68
Stretch	2.79	2.71	2.62
Bend	16.54	11.74	11.34
Stretch-Bend	0.43	0.32	0.34
Torsion	18.25	21.88	19.67
Non-1,4 van der Waals	-1.56	-2.10	-2.16
1,4 van der Waals	13.11	13.92	12.87
Dipole/Dipole	-1.73	-2.03	-2.00

trans-bond highlighted in cycloalkene compound 10

From the data of the total energy calculated by the two force fields, it can be noted that they both show that the total energy is greatest for 9 (chair) and least for 10 in the chair conformation. From the other data collected from the MM2 force field it appears that the greatest difference which stabilises both 10 conformations is due to their relatively less deviation from normality for bending than 9.

In 1924 Bredt noted that "double bonds tend to avoid ring junctions", however this intermediate reacts slowly during functionalisation across the double bond, which classify this bridgehead alkene as anti-Bredt.

Orbital overlap explanation

More recently it has been shown that bridgehead alkenes of larger polycyclic systems might actually be preferred as they result in hyperstability and that trans-cycloalkenes with a ring size of nine or more fall within this category. These types of olefins are so-called "hyperstable" as they are less strained than their fully saturated hydrocarbons counterparts. This extra stability has been suggested to come from partial rehybridisation of the p-orbitals so that they become closer in character to a tetrahedral sp³ carbon therefore resulting in a greater orbital overlap (and greater flexibility) - see diagram left.

Modelling Using Semi-Empirical Molecular Orbital Theory

Using molecular orbital methods including MOPAC/PM6 and MOPAC/PM1, the role of orbital control in reactivity will be considered for two further case-studies; that of the regioselective addition and the anomeric effect/neighbouring group participation in a glycosidation reaction.

Regioselevtive Addition of Dichlorocarbene

In order to take the role of electrons in molecules into account, a quantum mechanical treatment becomes necessary as this can be used to incorporate the wave-description of electrons. This method was used to investigate the orbital control of reactivity of 9-chloro-1,4,5,8-tetrahydro-4a,8a-methanonapthalene, 12 with electrophilic reagents.

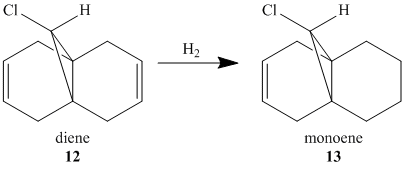
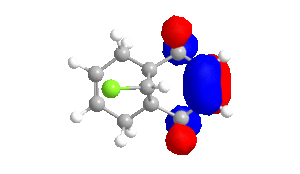
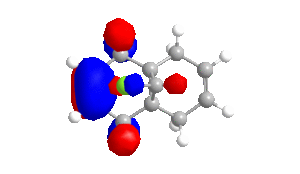
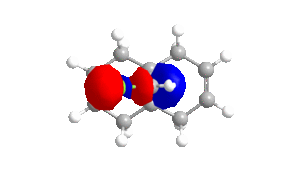
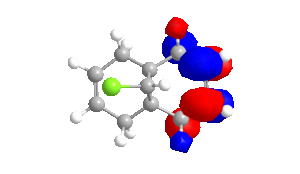
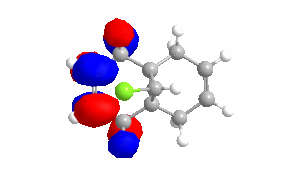
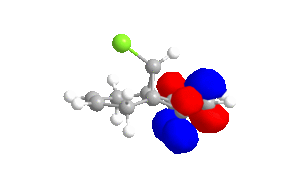
To obtain approximations for the valence-electron molecular wavefunction of compound 12, the structure was drawn and subsequently subjected to MM2, MOPAC/PM6 and MOPAC/RM1. The data presented below is from MOPAC/RM1 as this produced the best results for this investigation. Table 4 includes images of the five relevant molecular orbitals which were constructed during this analysis both from a top view and side view.

Table 4 - Molecular Orbitals of Compound 12

HOMO-1	HOMO	LUMO	LUMO+1	LUMO+2

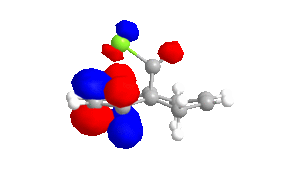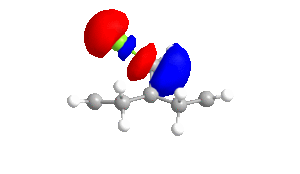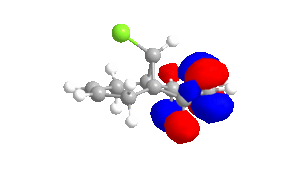The shape of the orbitals was considered and as a result of the shapes RM1 was found to be a better match for this molecule. It can be noted that the LUMO+1 and LUMO+2 are opposites of each other. Further the HOMO-1 and the HOMO look as expected with orbitals shaped like pi bonds over the two double bonds in the molecule. It can be noted that the HOMO molecular orbital (MO) is the molecular orbital most likely to react towards electrophilic attack, therefore from observations of the HOMO MO, it can be suggested that the endo alkene is the more nucleophilic of the two alkenes and would be the location of electrophilic addition, for example of chlorocarbene.

In addition, the influence of the Cl-C bond on the vibrational frequencies of this molecule is of interest and can be considered by comparing compound 12 with its exo-hydrogenated counterpart, compound 13. In order to do this the structures of both compounds were optimised using MOPAC/PM6 in ChemBio3D, symmeterized in Gaussian and finally IR spectra were generated by running B3LYP/6-31G(d,p). The data from these spectra pertaining to C=C and C-Cl bonds are summarized in Table 5.

Table 5 - Spectra Results for Compound 12 and 13

Compound	12 - Diene	13- Monoene
Symmetry	Cs and C1	C1
IR Spectra
Cl-C Stretching Vibration (cm-1)	770.87	774.95
C=C Stretching Vibration (cm-1)	1737.04 and 1757.35	1758.08

The two spectra are very similar in appearance with the peaks for both Cl-C and C=C occurring at approximately the same value. There are several more bands in the spectrum of compound 13 which is expected as compound 13 has less symmetry than compound 12. The largest difference between the two, for these vibrations, is the difference of approximately 4 cm^-1 for the Cl-C frequencies.

Monosaccharide Chemistry: Glycosidation

Glycosidation of sugars follows the general reaction:

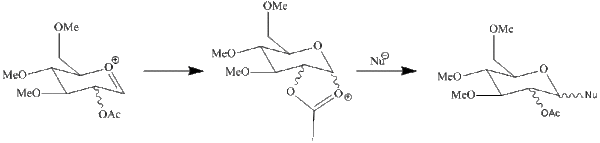
In this reaction the starting point determines whether the product is an α-anomer or β-anomer; two different anomers which have almost completely different diastereospecificity depending on the OAc orientation as a result of neighbouring-group-participation.

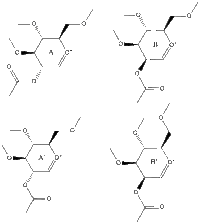
Table 6 summarizes data pertaining to the starting molecule which can be arranged in one of four structures (A, A', B or B'). In constructing this table methyls were used to replace R. Hydrogens would also have been appropriate for representing the chemistry of sugars however methyl groups keep computational demands to a minimum almost as well and it can be suggested that they result in relatively larger values and therefore differences between energies can be more easily assessed.

Table 6 - Data for Glycosidation Starting Molecule

Structure	A	A'	B	B'
Jmol
Acetyl position	below ring	below ring	above ring	above ring
Hydrogens (newly formed 5-membered ring)	cis	trans	cis	trans
MM2	19.48	33.10	24.25	37.90
MOPAC/PM6	-91.66	-77.40	-88.73	-68.23

As the data for Table 6 used two force fields (MM2 and MOPAC/PM6) it is possible to compare values to a certain extent between the four structures for each of these force fields. It is possible to conclude that A<A' and B<B' suggesting that a conformation in which the acetyl group is arranged with so that there is orbital overlap between oxygens of the acetyl group and the oxygen of the ring are most stable. Additionally from these values it would appear that in general A<B which is likely due to the fact that the A structures have fewer groups axial and is therefore more stable than the B structures. For these calculations there appears to be little difference between MM2 and MOPAC/PM6.

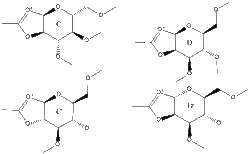
The intermediate in the glycosidation can also adopt four different structures (C, C', D and D') and data for these is summarized in Table 7.

Table 7 - Data for Glycosidation Intermediate

Structure	C	C'	D	D'
Jmol
Acetyl position	below ring	below ring	above ring	above ring
Hydrogens (newly formed 5-membered ring)	cis	trans	cis	trans
MM2 (kcal mol-1)	34.53	47.88	25.69	44.67
Angle C-C-O MM2 (°)	110.18	120.48	114.15	120.62
Angle O-C-O MM2 (°)	113.86	122.07	115.56	123.80
Bond Length (C)-C-O MM2 (A)	1.41	1.41	1.41	1.41
Bond Length (O)-C-O MM2 (A)	1.40	1.40	1.40	1.40
MOPAC/PM6 (kcal mol-1)	-91.66	-66.84	-91.37	-64.68
Angle C-C-O MOPAC/PM6 (°)	105.94	121.09	108.38	121.58
Angle O-C-O MOPAC/PM6 (°)	104.74	111.98	105.81	112.95
Bond Length (C)-C-O MOPAC/PM6 (A)	1.49	1.49	1.48	1.49
Bond Length (O)-C-O MOPAC/PM6 (A)	1.60	1.53	1.50	1.51
Stabilisation Energy	24.82		26.69

Anomeric Effect

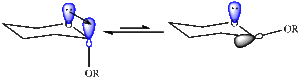
The four structures were again evaluated using both the MM2 and MOPAC/PM6 fields, however in this case the two methods did yield different results. While the prime (') structures were again higher in energy, with MM2 the D structures appeared to be lower in energy, however with MOPAC/PM6 the C structures are lower in energy. Additionally bond angles and lengths were different between the two force fields. Therefore in this instance the differences show that it is more beneficial to use MOPAC/PM6 for this analysis as it takes orbitals into account whereas MM2 attempts to reach an optimised geometry based solely on achieving optimum bond lengths and angles as is illustrated by this data. Therefore it can be concluded that the C structures will have lower energy as they benefit from the anomeric affect (see diagram right) which the D structures cannot achieve.

Structure Based Mini Project Using DFT-based Molecular Orbital Methods

Introduction

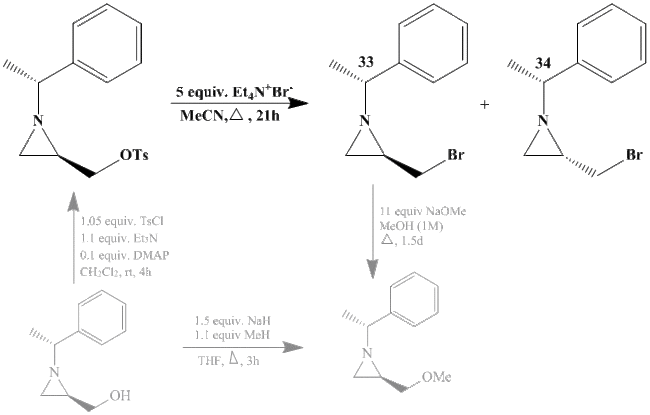
This mini project investigates two intermediate (33 and 34) in a synthesis of an aziridine compound, with the reaction above (bold reaction is the part in question, other parts of the reaction are shown, in grey, to give context to the issue). This is an interesting reaction as aziridines are important three-memebered ring systems as they are syntheically flexible, have unusual reactivity combinations and generally have good atom economy. This reaction was chosen because it is a useful synthetic reaction for organic chemists and the two compounds chosen from this synthesis are suitable for computational analysis as they are relatively small and rigid.

As these are pseudo-enantiomers of each other (i.e. they differ by one chiral center while however there are other chiral centers as well), it is unlikely that there will be significant differences in NMR, IR or MS therefore the main spectroscopic method that can be used to distinguish between 33 and 34 is likely optical rotation and literature quotes these values as [α]²⁸_D = +15.5 and [α]²⁸_D = +80.2 for 33 and 34, respectively.

Please note that all literature values for these two compounds are from the reference:.

¹³C NMR

To compare a computational approach with experimental data for compound 33 and 34 from literature, a GIAO approach was used to predict the ¹³C NMR spectra. Initially the structures were optimised in order to obtain a NMR spectrum for the literature conformation. Table 1 includes Jmol rotatable images for the two optimised structures as well as links to the NMR spectra which were uploaded to the Digital repository.

Table 1 - Digital Data

Enantiomer 33	Enantiomer 34
DOI:10042/to-9506	DOI:10042/to-9517

Table 2 contains a comparison of the NMR spectrum for compound 33 to the data reported in literature and Table 3 contains the same for four different conformations of compound 34 with comparisons to literature. For the data in Table 2 and Table 3 the root mean square (RMS) was calculated in order to determine how closely the theoretical data compared to the results from the literature report. As a result of calculating the RMS value, compound 34 has three additional sets of data which correspond to different conformations. This demonstrates how ¹³C NMR shifts can be used for conformational analysis.

Carbon Numbering Reference

Table 2 - ¹³C NMR Comparison for Enantiomer 33

	Comments	Literature / ppm	Gaussian / ppm
C1 - CH2	CH2-Br*	35.9	35.0
C2 - CH	aziridine ring	41.2	41.0
C3 - CH2	aziridine ring	35.3	34.5
C4 - CH3	Me	23.7	27.1
C5 - CH	CH-CH3	69.6	69.7
C6 - C	ring	144.2	141.8
C7 - CH	ring - ortho**	127.2	123.4
C8 - CH	ring - meta**	128.5	124.8
C9 - CH	ring - para	126.9	123.5
	RMS		2.5

*value shown includes -12 for C-Br correction **average of 2 values

Table 3 - ¹³C NMR Comparison for Enantiomer 34

	Comments	Literature / ppm	Gaussian 1 / ppm	Gaussian 2 / ppm	Gaussian 3 / ppm	Gaussian 4 / ppm
C1- CH2	CH2-Br*	39.5	35.2	31.2	34.7	40.1
C2 - CH	aziridine ring	35.5	32.3	38.2	40.7	42.1
C3 - CH2	aziridine ring	34.8	28.3	34.4	34.2	36.4
C4 - CH3	Me	23.1	21.3	27.4	26.8	27.3
C5 - CH	CH-CH3	69.8	59.8	62.8	69.4	69.1
C6 - C	ring	144.1	132.1	141.7	141.4	142.2
C7 - CH	ring - ortho**	127.3	126.1	123.1	123.1	123.8
C8 - CH	ring - meta**	128.4	124.4	124.5	124.5	125.2
C9 - CH	ring - para	127.0	127.3	123.3	123.1	123.9
	RMS		6.1	4.7	3.6	3.3

*value shown includes -12 for C-Br correction **average of 2 values

For both of these molecules the ¹³C NMR data fell within the suggested range of values as there was only one value with a difference greater than 5ppm (for 33 and 34-4). This is again reiterated with the root mean squared values which show that the average difference from the literature values was 2.5 and 3.3. Especially for 34 one of the main sources of variation came from C1 and C2. For C1 this was corrected using a known spin-orbit coupling error correction (for C-Br subtract 12) however for 34, C2 could also have used a correction factor as it was the only shift to have a difference greater than 5. This illustrates that while DFT calculations are a good method for predicting this type of data there are still limitations to the accuracy (which are likely due to the small changes in conformation).

³J H-H Coupling

Hydrogen Numbering Reference

The ¹H coupling constants were calculated using Janocchio, and the optimized structure that was also submitted for ¹³C NMR. The data collected from this program is summarized in Table 4 and Table 5 below.

Table 4 - Coupling Constants for ¹H NMR for Enantiomer 33

Environment	Shift / ppm	Integral	Multiplicity	Literature J / Hz	Theoretical J / Hz	% Difference
6	1.44	3H	d	6.6	6.09	8%
trans (4/5)	1.44	1H	d	6.6	9.55	45%
cis (4/5)	1.6	1H	d	2.8	9.26	231%
3	1.85-1.89	1H	m	-	-	-
7	2.42	1H	q	6.6	6.09	8%
1 and 2	3.17 and 3.44	2H	2 x dd	10.5	11.34	8%
				8.3
				3.5	4.68	34%
8	7.15 - 7.30	5H	m	-	-	-

Table 5 - Coupling Constants for ¹H NMR for Enantiomer 34

Environment	Shift / ppm	Integral	Multiplicity	Literature J / Hz	Theoretical J / Hz	% Difference
6	1.42	3H	d	6.6	6.08	8%
trans (4/5)	1.64	1H	d	6.6	9.58	45%
cis (4/5)	1.88	1H	d	3.3	9.27	181%
3	1.80-1.90	1H	m	-	-	-
7	2.53	1H	q	6.6	6.08	8%
1 and 2	3.13 and 3.31	2H	2 x dd	10.2	11.35	11%
				6.9
				5.8	4.70	19%
8	7.24 - 7.37	5H	m	-	-	-

From this data it can be seen that for both 33 and 34 there were 2 coupling constants (environments 6 and 7) which corresponded quite well with the experimental/literature data, 2 coupling constants (environments 1 and 2 for the ³J values) which were in the region of the expected values, 2 coupling constants that were not suitable to be calculated with this method (environments 4 and 5) and one ²J coupling constant which could also not be determined using this method (environment 1 and 2 for the ²J value).

As a result, it was attempted to obtain more accurate data which would hopefully have distinguished between the cis and trans coupling constants (environments 4 and 5) by using a DFT calculation for coupling constants however, either due to the input or to the calculation, this also produced values which were not viable. The log output file for this was: File:34 NMR Output 3a Log File log 46899.out.

Vibrational (IR) Spectra

Using DFT method B3LYP the IR spectra for compounds 33 and 34 were constructed and analyzed using Gaussian to correlate the main peaks of the predicted IR frequencies with their vibrational counterparts. A literature reference was consulted for characteristic IR frequencies of aziridine. Table 6 contains data for enantiomer 33 and Table 7 contains data for enantiomer 34. Additionally on the right are the spectra obtained using DFT; for compound 34 the IR assignments of significant frequencies have been indicated.

IR Spectrum of 33

Table 6 - IR Data for 33

Vibrational Mode	Literature	Computational
asymmetric CH (ring) stretch		3202.43
asymmetric CH3 stretch		3137.49
symmetric CH3 stretch		3048.74
asymmetric CH2 stretch, aziridine	3034
symmetric CH2 stretch, aziridine	2964, 2923 and 2838	3123.44
CH stretch		2937.1
CC ring stretch, aromatic	1493, 1450 and 1422	1392.34
symmetric ring breathing, aziridine	1223	1280.63 and 1216.88
CN stretch	1165	1110.18
CH bend	985
CH2 rock/ring deformation, aziridine	758	776.76
CH oop, aromatic	702	717.21
C-Br stretch	629	650.08

Annotated IR Spectrum of 34

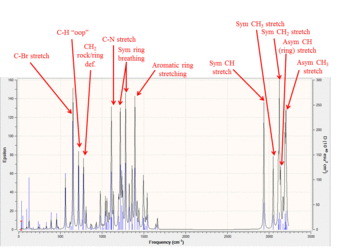
Table 7 - IR Data for 34

Vibrational Mode	Literature	Computational
asymmetric CH (ring) stretch		3202.43
asymmetric CH3 stretch		3137.49
symmetric CH3 stretch		3048.74
asymmetric CH2 stretch, aziridine	3026
symmetric CH2 stretch, aziridine	2968, 2926 and 2837	3109.13
CH stretch		2937.01
CC ring stretch, aromatics	1493 and 1448	1392.34
Symmetric ring breathing, aziridine	1240 and 1222	1280.74 and 1216.87
CN stretch	1069	1110.17
CH bend	971
CH2 rock/ring deformation, aziridine	755	776.77
CH oop, aromatic	698	717.21
C-Br stretch	640	650.15

From this data it can be seen that while most of the important vibrations necessary to characterise the two compounds are present, there are still significant differences in the values. Some of these could perhaps be corrected by up to 8% however the main shortcoming of this computational method is that the two enantiomers cannot be distinguished as the calculations produced almost identical results for the majority of the vibrations.

Additionally from the log output files it was possible to find the value for the 'sum of electronic and thermal free energies' for both enantiomers. This was reported as being -3053.860156Ha and -3053.860155Ha for 33 and 34 respectively, giving -4.8667 kcal/mol for both (to four decimal places). This very slight, almost non-existent difference in energy is expected as these two compounds differ only in the geometry of one bond.

Optical Rotation

As literature reports that these two compounds were separated (relative yield of 2:1) there must be a physical difference between them and from literature it would appear that this is the retention factor as 33 has R_f=0.31 and 34 has a R_f=0.51 in petroleum ether/EtOAc 4:1. However the only computational method which is likely to distinguish between the two compounds would be the measurement of the optical rotation or a prediction of the electronic circular dichroism spectra.

For compound 33 the reported optical rotation is: [α]²⁸_D = +15.5. Using the DFT version cam-B3LYP this was found to be:[α]²⁸_D = +137.58 deg. This does have the correct sign, the magnitude of this value is out by a factor of 10 which is expected as this type of calculation is susceptible to large errors due to minor changes in geometry.

Unfortunately a value for 34 can not be reported. The input files which wereused to attempt this calculation are: File:34 Optical Rotation Input 3a.gjf, File:34 Optical Rotation Input 3a 2.gjf and File:34 IR Optical Rotation 3a NEW.gjf. In addition it was attempted to find the electronic circular dichroism spectrum of 34 however this was also not possible to report a result from this. The input files which were used to attempt this calculation are: File:34 3 for CD.gjf and File:34 CD Spectrum Input.gjf. Please note that these files have been listed chronologically in order of uploading to SCAN.

Conclusion

This mini project investigated the differences between two pseudo-enantiomers of a compound with an aziridine ring. The main aim was to compare data from literature against computational calculations in order to determine the accuracy of these calculations and their possible use for determining which product has formed; to that end it was also important to observe whether the calculations could distinguish between the two forms.

It was found that while this level of calculation (DFT, MPW1PW91) is suitable for optimising the geometries and can be used to some extent to predict ¹³C NMR, there are severe limitations especially due to the structure of the aziridine ring when attempting to predict ¹H NMR(coupling constants). Further, the main method of spectroscopically distinguishing between the two forms was not viable with using this level of sophistication as small changes had proportionately larger effects on the optical rotation.

If this investigation were to be continued, it would be interesting to find the optical rotation of 34 as well as compare circular dichroism spectra. Further this project could be expanded by considering how the reaction which forms 33 and 34 is controlled and as a result why the ratio of products is 2:1.