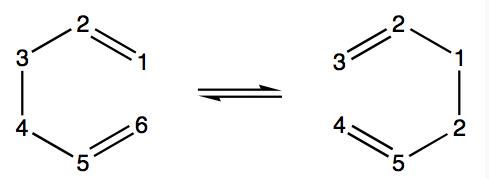Rep:Mod:zxcv1234physical

The Cope Rearrangement

Cope Rearrangement

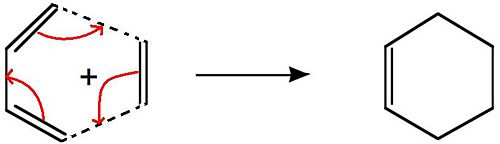
1,5-hexadiene undergoes a [3,3]-sigmatropic shift rearrangement, which has been extensively studied and called the Cope Rearrangement. The general reaction scheme for this rearrangement is shown on the right. It is now generally accepted that the mechanism is a concerted process going through either a boat or chair conformation, but in the past the mechanism caused great discussion. In this project the B3LYP/6-31G* method and basis set willl be used to give an approximation of the activation energies and enthalpies and they will be compared to literature to see how close they coresspond to experimental values.

Optimising Reactants and Products

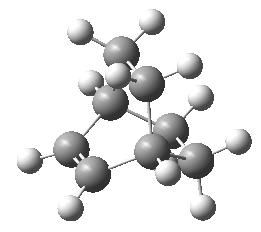
A molecule of 1,5 hexadiene was drawn with the central 4 carbon atoms in a anti-periplanar arrangement. The structure was first cleaned using the Gaussview clean function and then optimised using the Hartree Fock method with a 3-21G basis set. The structure that was returned was the one on the right. The energy of which was -231.69269237 a.u.. The symmetrize function of Gaussview returned the point group of C2 which appears correct from the 3D structure. The criterea didn't have to be relaxed to return this answer and relaxation of the symmetry had no effect.

1,5 Hexadiene Anti1

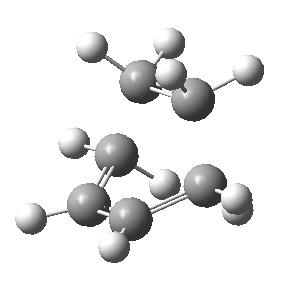
Another molecule of 1,5 hexadiene was drawn but this time with the 4 central carbons in gauche conformation. The exact same method as before was used to optimise the structure. I would expect this structure to return a higher energy than the first as in general there is more steric-hindrance in a gauche conformation in comparison to an anti-periplanar relationship. The structure was infact returned with a higher energy of -231.69153023 a.u.. The structure was again symmetrised to return a point group of C2.

1,5 Hexadiene Gauche1

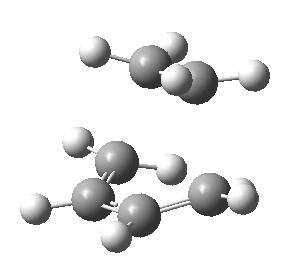
Based on the previous two calculations I would estimate that the lowest energy conformation of this molecule would be with the central 4 carbons in an anti-periplanar relationship, as this returned the lowest energy value in the previous two calculations. However in would imagine that a lower energy could be achieved by having the alkene groups pointing up and down respectively out of the plane of the anti-periplanar relationship of the central 4 carbons. This produces the structure on the right but it actually has a higher energy than the first conformation of -231.69253524 a.u.. The point group of this molecule is Ci.

1,5 Hexadiene Anti2

Upon comparison of the structures optimised by myself with the appendix provided, I had not yet discovered the lowest energy conformation. The structures I had optimised were anti1 gauche3 and anti2. The energies of my optimised structures were almost exactly the same, only differing by the final decimal number. Conformer anti1 and what I thought would be the lowest energy anti2 were actually the 2nd and 3rd lowest conformers respectively. The lowest energy conformer, as given in the appendix is gauche3. This outcome is extremely unexpected so I decided to optimise the lowest energy conformer at a higher level of theory as well as the C_i conformer that I would have expected to be lowest in energy. Both these were optimised at a B3LYP/6-31G* level.

At this higher level of theory the relative energies were different and the C_i conformer was lower in energy than the lowest energy conformer at the lower level of theory calculation. The table below shows a few of the differences between the high and low level calculations of the C_i conformer and the previous lowest energy conformer gauche3.

Anti 1 Ci	Gauche 3 C1
1,5 Hexadiene Anti2	1,5 Hexadiene Anti3
3-21G 6-31G* Energy (a.u.) -231.69253521 -234.61171622 Energy Difference (kcal/mol) 0 -1831.81-3 C2-C3-C4/C3-C4-C5 Bond Angle 111.344° 112.681° C1-C2 Bond Length (Å) 1.31614 1.33350 C2-C3 Bond Length (Å) 1.50887 1.50411 C3-C4 Bond Length (Å) 1.55319 1.54810	3-21G 6-31G* Energy (a.u.) -231.69266121 -234.61132932 Energy Difference (kcal/mol) 0 -1831.49-3 C2-C3-C4/C3-C4-C5 Bond Angle 111.772,111.871° 113.465,113.478° C1-C2 Bond Length (Å) 1.31631 1.33361 C2-C3 Bond Length (Å) 1.50845 1.50438 C3-C4 Bond Length (Å) 1.55323 1.55323

There are not huge differences in the geometries between the two levels of theory. The most important observation is the reversing of the relative energies. At the lower level HF/3-21G Gauche 3 is 0.079 kcal/mol lower in energy but at the the higher level Anti 2 is 0.243 kcal/mol lower in energy. I am confident that Anti 2 with point group C_i is the lowest energy conformer and this is generally the case in the literature

The vibrational modes of the optimised structure were calculated at the B3LYP/6-31G* level. This is an important way to characterise that a minimum in energy has been achieved by the absence of imaginary vibrational frequencies. There were no imaginary vibrations confirming the minimum and the IR Spectrum looked as below.

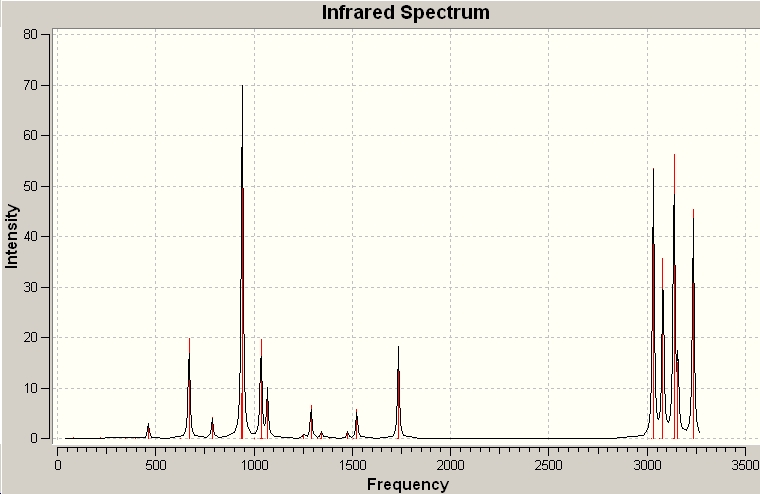
From this calculation the following information could also be obtained.

Sum of Electronic and Zero-point Energies	-234.469212 a.u.
Sum of Electronic and Thermal Energies	-234.461854 a.u.
Sum of Electronic and Thermal Enthalpies	-234.460910 a.u.
Sum of Electronic and Thermal Free Energies	-234.500840 a.u.

Optimizing the Chair and Boat Transition Structures

Optimising to a Transition State (Berny)

Chair Transition State Guess

An allyl fragment of CH₂CHCH₂ was created in Gaussview and then optimsied at a Hartree Fock/3-21G level. The output of this was the then copied to create the same fragment twice. The second fragment was rotated 180° and raised to a height of 2.2 Å above the other. This was the guess for the chair transition state and it looked like the image on the right.

This guess was then used to calculate the transition state. An optimisation and frequency calculation was done at the HF/3-21G level and the structure was optimised to a Berny Transition State. In Gaussian in the additional words box, "Opt=NoEigen" was typed to stop the program crashing if more than one imaginary frequency was calculated, which can happen if the inital guess is too far from the actual answer. However, the output showed only one imaginary frequency. This is the frequency relating to the cope rearrangement and is at -817.887 cm-1. The form of the vibration is shown on the left.

Frozen Coordinate Method

The same guess structure as used before was openned in a new molecule window. The Redundant Coord Editor was then selected from the Gaussview edit menu. Two identical coordinates were set up between adjacent terminal carbons between fragments. The parameters were set as Bond and Freeze Coordinate. This structure was then optimsised as if it were a normal minimisation at the HF/3-21G level.

This gives a structure similar to the one previously calculated using the Minimisation to a Berny Transition State except the bond forming/breaking distnaces are fixed at 2.2Å These bonds were then optimised as well to give a more accurate representation of the transition state. This was done by selecting the same bonds that were fixed before but changing the parameters to Bond and Derivative. A transition state optimisation was then done as before in the first method, except the force constants were never calculated.

The table below shows some of the data obtained from both methods.

Method	Optimised to a Transition State	Frozen Coordinate
Imaginary Frequency	-817.887 cm-1	-818.011 cm-1
Bond Forming/Breaking Length	2.02026Å	2.02049/2.02052Å

Both methods have given a very similar result. This is not suprising as this is a very small and uncomplicated molecule that is being formed, with no room for conformational differences.

Optimising the Boat Transition State Using the QST2 Method

The QTS2 Method works by interpolating between two structures in order to find a the transition state between them. To do this the product and starting material have to numbered in a way that will give rise to the correct transition state. In the case of the cope rearrangement it is required that the molecules are numbered as follows...

In Gaussview 2 molecules of the the optimised Anti 2 1,5 Hexadiene were pasted into the same "MolGroup". Using the atom list function within Gaussview the two molecules were numbered in the same fashion as the schematic shown above. The reactant and product looked as follows...

A QTS2 calculation was then run by selecting an Opt + Freq calculation and selecting Optimise to a TS (QTS2). This job failed and the result can be seen below as a jmol. It failed because during the calculation it did not consider rotation about the central C-C bond and just translated the two allyl fragments. The result was similar to the boat transition state but with the two fragments further apart.

Failed Boat TS QTS2

To help the calculation find the transition state the rotation about the central C-C bond was done prior to running the calculation. The result of these rotations made the new starting material and product look like this...

With these new reactant and product the same QTS2 calculation was run as before, but this time the boat transition structure was produced. The structure of this is shown below.

Boat TS

This the boat transition state of the cope rearrangement. There is one imaginary vibration at -839.725 cm-1 and it does correspond to the rearrangement.

The Intrinsic Reaction Coordinate

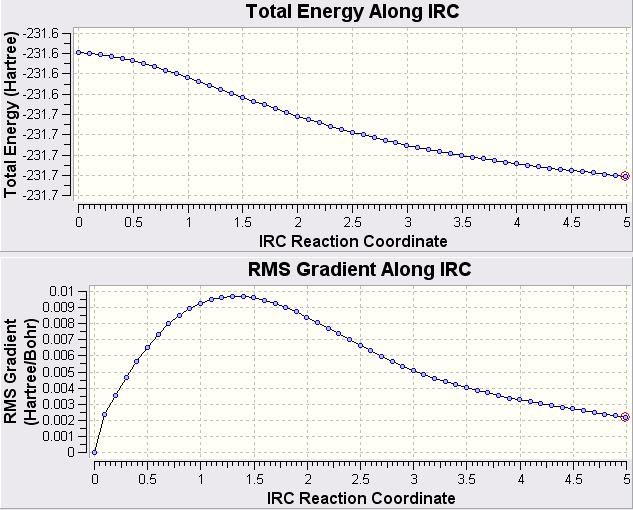
The optimised boat transition structure from the HF/3-21G, optimised to a Berny Transition State was used to measure the reaction path using the IRC method. This was done by selecting Calculate Gaussian and choosing the job type as IRC. The calculation was only run in the forward direction as this is a symmetrical process, the force constants were calculated at the start and the number of points was set to 50. The plot of the Total Energy during the IRC and the RMS Energy Gradient are shown below.

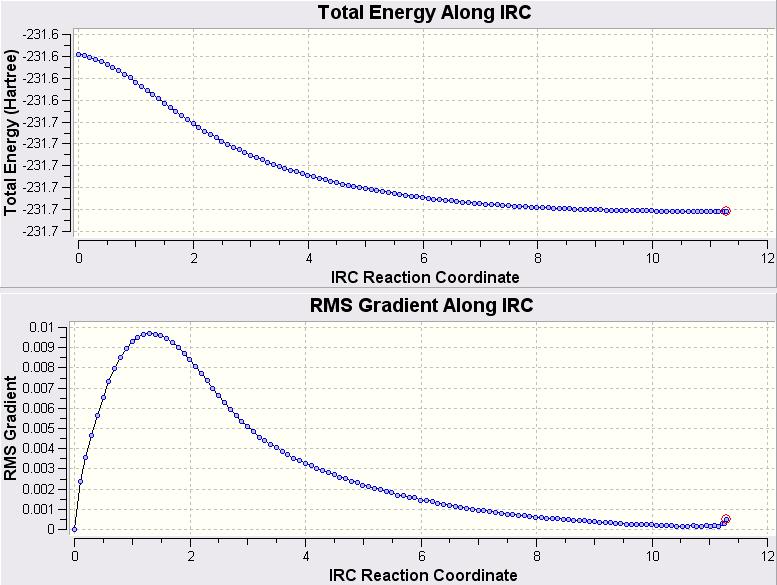
From these graphs it is clear that the calculation is yet to reach a minimum. It was decided that the calculation would be repeated from the start but this time using 120 points as this seemed to be plenty. The resulting IRC graphs are shown below.

At the very end of this the RMS Gradient is starting to rise again. This is perhaps suggesting that if it had been left to go on for longer then it would of perhaps went off in the wrong direction. Apart from a slight deviation at the end, it does appear that the structure has reached a pretty good minimum and ~110 points would of been a good amount of points to calculate the reaction path to a minimum.

Activation Energies

The transition states for both the chair and boat were re-optimised at the higher level of theory of B3LYP/6-31G*. The table below shows a comparison of the energies and some geometric measurements from both levels of theory.

Chair	Boat
HF/3-21G B3LYP/6-31G* Energy (a.u.) -231.61932240 -234.55698291 Energy Difference (kcal/mol) 0 -1843.41 TS Vibration (cm-1) -817.887 -565.533 C1-C2-C3/C4-C5-C6 Bond Angle 120.505,120.510° 119.960,119.963° Distance between fragments (Å) (at terminal carbons) 2.02026 1.96759,1.96750	HF/3-21G B3LYP/6-31G* Energy (a.u.) -231.60280244 -234.54309304 Energy Difference (kcal/mol) 0 -1845.06 TS Vibration (cm-1) -839.725 -530.58 C1-C2-C3/C4-C5-C6 Bond Angle 121.693,121.693° 122.268,122.268° Distance between fragments (Å) (at terminal carbons) 2.14013 2.20614

This table shows that between the different levels of theory the geometries of the transition states are pretty much the same but the energies, especially the energy of the imaginary vibration are very different. It is then fair to say that only quick low level calculations are required to look at the shape of transition states but that a higher level should then be used to estimate energies.

The activation energies can then be calculated by looking at the difference in energy of the ground state 1,5-hexadiene molecule and the energies of the transition states. All of the energies given are at 0K so the activation energies of the two transition states are...

0K
Chair - 34.346 kcal/mol
Boat - 43.062 kcal/mol

The activation energies can also be calculated at room temperature by looking at the Sum of the Electronic and Thermal energies, found in the results file. This gives the activation energies at room temperature as...

298.15K
Chair - 33.163 kcal/mol
Boat - 41.320 kcal/mol

The experimental values for the activation energies for the chair and boat transition states at 0K are 33.5 ± 0.5 kcal/mol and 44.7 ± 2.0 kcal/mol respectively. The calculated activation energy for the boat transition state falls within the margin but the calculated chair transition state falls just outside of the experimental values window. However the estimations are still extremely good considering how quickly these results were achieved in comparison to how long it would take to obtain the experimental values.

The Diels Alder Cycloaddition

The Diels Alder cycloaddition reaction is a pericyclic reaction between an alkene and a 1,3-diene. The reaction proceeds in a concerted fashion. The π orbitals of the dieneophile (alkene) are used to form new σ bonds to the diene. The general scheme for the cycloaddition is shown below.

Optimisation of Cis-Butadiene and Ethene

Cis-butadiene was built in gaussview and then the structure was optimised using a AM1 semi empirical molecular orbital method. The HOMO and LUMO molecular orbitals generated are shown below.

HOMO	LUMO
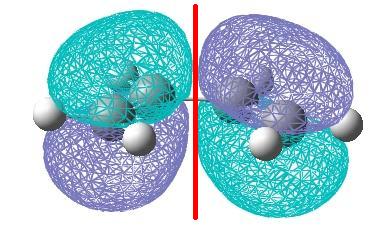
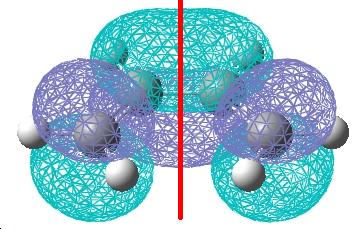
The HOMO orbital is anti-symmetric with respect to the plane.	The LUMO orbital is symmetric with respect to the plane.

The same was done for the dienophile fragment of ethene.

HOMO	LUMO
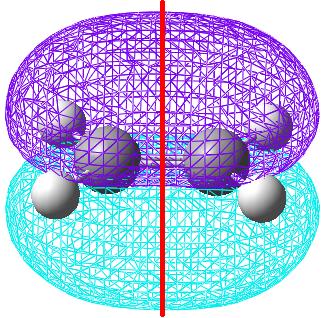
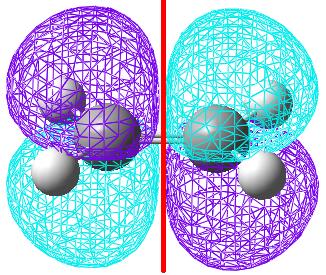
The HOMO orbital is symmetric with respect to the plane.	The LUMO orbital is anti-symmetric with respect to the plane.

The Transition State

The transition state was guessed by first optimising a structure of cyclohexene with a bridging C₂H₄ group joining at the 2 and 5 positions. This was optimised at the HF/3-21G level and the structure looked like the one below.

The bottom bridging C₂H₄ group was removed and where the C-C bonds had been a hydrogen was added. The two C-C bonds between the upper bridging C₂H₄ group were also broken. The frozen coordinate method was then used to optimise the transition state. The transition σ bond lengths were guessed as the same length as in the cope rearrangement as 2.2Å. The result of this was then optimised to Berny Transition State with the frozen coordinates replaced with Bond and Derivative instead. The result of this calculation is shown below.

The transition structure has one imaginary frequency at -956.502 cm^-1 and this shows that this is a concerted symmetrical process, in which the bonds are formed synchronously. The form of the vibration is shown below.

The first positive and real vibration is asymmetric in contrast.

This diagram shows some of the important geometric measurements of the transition structure. (All measurements are in Å)

The lengths of the new bonds being formed in the transition structure are 2.11915 Å this is longer than a normal sp³ C-C bond length at 1.54 Å but shorter than the distance of twice the van der waals radii of two carbon atoms at 2 x 1.70 Å.

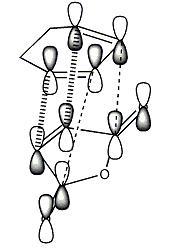
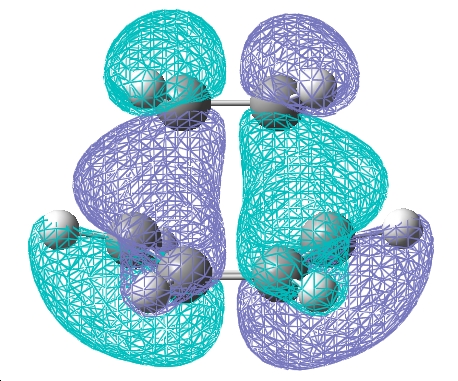
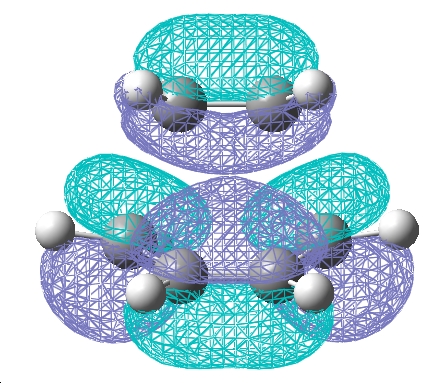
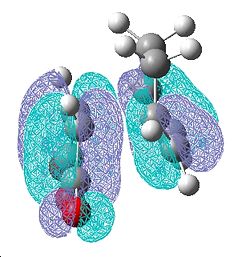
The frontier orbitals of the transition state are shown below.

HOMO	LUMO
The HOMO molecular orbital is anti-symmetric with respect to the plane. Upon comparison with the original fragments of the diene and dieneophile it is clear that this is a reaction between the HOMO of the diene and the LUMO of the dieneophile. The reaction is allowed because the two molecular orbitals that are coming together are of the same symmetry with respect to the plane.	The LUMO molecular orbital is symmetrical with respect to the plane.

Regioselectivity

When the dieneophile in a diels alder reaction is not ethene then regioselectivity becomes important. The diels alder has a high level of selectivity towards the endo product. Earlier work on the dimerisation of cyclopentadiene showed that in that case the endo product was higher in energy and that its selectivity to produce mainly endo was due to secondary orbital interactions producing the endo product under kinetic control. Calculations of the transition state in the diels alder reaction and analysis of the frontier orbitals will hopefully shed some light on this previous discussion.

The reaction that is going to be looked at is the diels alder cycloaddition of 1,3-hexadiene and maleic anhydride. The transition states of the two products were located by first creating the two products in gaussview and optimising them at a AM1 semi-empirical level. The two different products are shown below.

Exo Product	Endo Product
Exo Product	Endo Product

The bonds joining the maleic anhydride part of the molecule were then removed and the frozen coordinate method was used holding the distance between the fragments at 2.2 Å as before. The frozen coordinates were removed and the coordinates parameters set to bond and derivative as before. The structure was then optimised to a berny transition state and the vibration frequencies calculated. Images of the transition structures are shown below in the table with some key measurements.

Exo		Endo
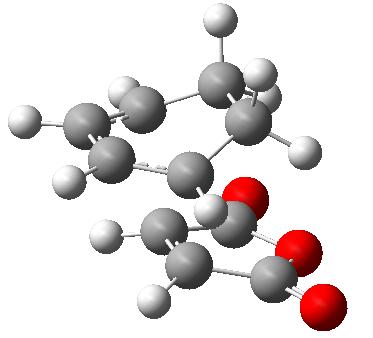
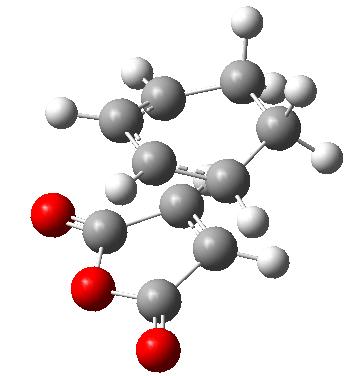
Energy (a.u.)	-0.05050326	Energy (a.u.)	-0.05159428
Energy Difference (kcal/mol)	0.685	Energy Difference (kcal/mol)	0
Imaginary Vibration Frequency (cm-1)	-811.445	Imaginary Vibration Frequency (cm-1)	-805.714
Length of Forming C-C Bonds in the Transition Structure (Å)	2.17044	Length of Forming C-C Bonds in the Transition Structure (Å)	2.16239

From this it can be seen the exo transition state is higher in energy by 0.685 kcal/mol. To see why this is the case the frontier orbitals will have to be analysed.

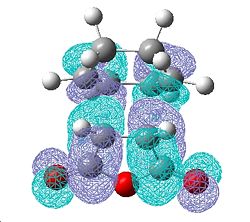
Exo Transition State
HOMO		LUMO
Front	Side	Front	Side

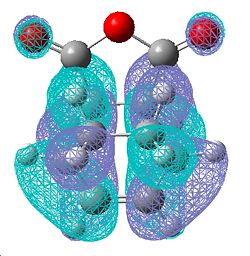
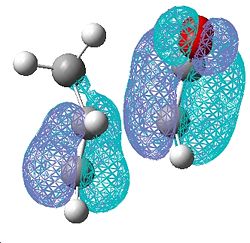
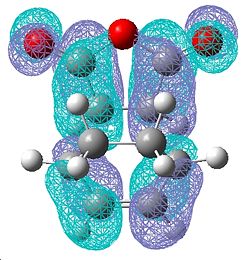
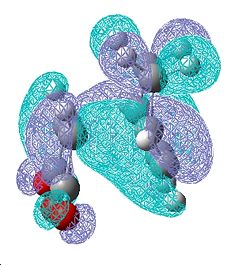
Endo Transition State
HOMO		LUMO
Front	Side	Front	Side

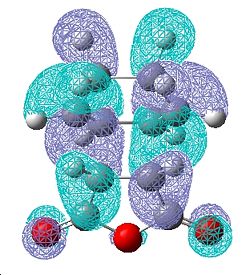
The secondary orbital interactions that I am looking for can be represented by this diagram, with the primary interactions in the bold dashed line and the secondary interactions represented by the line dashed line.

This diagram represents the interactions that make this reaction favourable to the endo product due to secondary overlap between the diene HOMO and the dienophile LUMO. These interactions are not present in the exo form due to lack of overlap. This is the basis behind the secondary frontier orbital explanation of the preference of endo. However, looking first at endo transition state, there is very little electron density between the maleic anhydride fragment and the diene other than the σ bond forming overlap. There is electron density in the diene in the area expected but no accepting orbital on the maleic fragment to overlap with this. In the case of the exo where there is supposed to be no interaction the case looks almost identical. The shape of the electron density between the two fragments is the same in both cases and fails to support any evidence of secondary orbital interactions being the cause of the stereoselectivity towards the endo production. The comparison of transition state energies did compute the same answer of preferred reaction path as the secondary frontier orbital interaction theory. The SFOI did provide a good rational to this particular problem but it doesn't actually hold true when looking at the calculated molecular orbitals instead of the simple linear combination of atomic orbitals.