Rep:Mod:zss0923
Inorganic computational lab (week 1)
Day 1
Optimizing BH3 molecule
A BH3 molecule was created, and the three B-H bond distances was changed to 1.53 Å, 1.54 Å and 1.55 Å respectively. Geometry optimization was carried out by Gaussian using B3LYP method and 3-21G as basis sets.
Analysing the optimised BH3 molecule using two basis sets
The optimised output log file is linked to here.
A table of important calculation information is given below:
| File type | .log |
| Calculation type | FOPT |
| Calculation method | RB3LYP |
| Basis set | 3-21G |
| E(RB3LYP) | -26.46226429 a.u. |
| RMS Gradient Norm | 0.00008851 a.u. |
| Dipole Moment | 0.00 Debye |
| Point Group | CS |
| Run time | 12.0 seconds |
The actual log file is checked to see whether the calculation has gone to completion:
Item Value Threshold Converged?
Maximum Force 0.000220 0.000450 YES
RMS Force 0.000106 0.000300 YES
Maximum Displacement 0.000709 0.001800 YES
RMS Displacement 0.000447 0.001200 YES
Predicted change in Energy=-1.672479D-07
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1947 -DE/DX = -0.0002 !
! R2 R(1,3) 1.1948 -DE/DX = -0.0002 !
! R3 R(1,4) 1.1944 -DE/DX = -0.0001 !
! A1 A(2,1,3) 120.0157 -DE/DX = 0.0 !
! A2 A(2,1,4) 119.9983 -DE/DX = 0.0 !
! A3 A(3,1,4) 119.986 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
We can find that all four values for force and displacement converged to a minimum which is lower than the Threshold value. And this indicates that our calculation has gone to completion.
Optimised B-H bond distance: 1.19 Å.
Optimised H-B-H bond angle: 120.0о
Using a better basis set for BH3 optimisation
This time we use a more accurate basis set 6-31G(d,p).
The optimisation output is here.
Important calculation information is reported below:
| File type | .log |
| Calculation type | FOPT |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| E(RB3LYP) | -26.61532360 a.u. |
| RMS Gradient Norm | 0.00000707 a.u. |
| Dipole Moment | 0.00 Debye |
| Point Group | CS |
| Run time | 5.0 seconds |
The below part of the log file is used to check if the calculation was complete:
Item Value Threshold Converged?
Maximum Force 0.000012 0.000450 YES
RMS Force 0.000008 0.000300 YES
Maximum Displacement 0.000061 0.001800 YES
RMS Displacement 0.000038 0.001200 YES
Predicted change in Energy=-1.069288D-09
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1923 -DE/DX = 0.0 !
! R2 R(1,3) 1.1923 -DE/DX = 0.0 !
! R3 R(1,4) 1.1923 -DE/DX = 0.0 !
! A1 A(2,1,3) 120.0055 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0007 -DE/DX = 0.0 !
! A3 A(3,1,4) 119.9938 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Obviously, all parameters have converged and our optimisation worked.
Optimised B-H bond distance: 1.19 Å
Literature reported B-H bond distance: 1.19 Å[1]
Optimised H-B-H bond angle: 120о
Day 2
Use of psuedo-potentials and large basis sets for GaBr3
For heavy atom i.e Group 3 or below, pseudo-potentials can be used to model the core electrons of an atom much easier. Here we want to study a 136-electron system GaBr3, and pseudo-potential is used with a medium level of basis set. It should be noticed that the symmetry of GaBr3 was restricted to D3h.
The output files are here: DOI:10042/26063
Important calculation information is summarized below:
| File type | .log |
| Calculation type | FOPT |
| Calculation method | RB3LYP |
| Basis set | LANL2DZ |
| E(RB3LYP) | -41.70082783 a.u. |
| RMS Gradient Norm | 0.00000016 a.u. |
| Dipole Moment | 0.00 Debye |
| Point Group | D3h |
| Run time | 14.1 seconds |
A check if the calculation was correct or not:
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000003 0.001800 YES
RMS Displacement 0.000002 0.001200 YES
Predicted change in Energy=-1.282691D-12
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 2.3502 -DE/DX = 0.0 !
! R2 R(1,3) 2.3502 -DE/DX = 0.0 !
! R3 R(1,4) 2.3502 -DE/DX = 0.0 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Obviously, the optimisation did converge.
Optimised Ga-Br bond length: 2.35 Å
Literature reported Ga-Br bond length: 2.249 Å[2] (measured via Gas Phase Electron Diffraction)
Optimised Br-Ga-Br bond angle: 120.0о
It is found that literature Ga-Br bond length is shorter than our prediction, and this may infer that a more high level of basis set is needed to get a more accurate bond length. What's more, calculation did not consider the crystal packing, so the experimental bond distance is smaller. Finally, Gaussian calculation was carried out when the molecule is in its gas phase. And in literature, solid crystals was used to determine the bond length. Thus, solid phase structure packs more tightly than gas phase structure, and it explains the bond length difference. Generally, my optimisation result seems reasonable.
Using a mixture of basis-sets and psuedo-potentials
A mixture of pseudo-potential and full basis set is used when the compound contains both heavy atoms and light atoms. Here BBr3 is under investigation. A LANL2DZ and 6-31G(d,p) basis set is used on Br and B respectively.
Output files: DOI:10042/26064
Summary information is reported below:
| File type | .log |
| Calculation type | FOPT |
| Calculation method | RB3LYP |
| Basis set | Gen |
| E(RB3LYP) | -64.43644739 a.u. |
| RMS Gradient Norm | 0.00000939 a.u. |
| Dipole Moment | 0.0002 Debye |
| Point Group | CS |
| Run time | 20.8 seconds |
A quick check on the output of log file:
Item Value Threshold Converged?
Maximum Force 0.000021 0.000450 YES
RMS Force 0.000010 0.000300 YES
Maximum Displacement 0.000135 0.001800 YES
RMS Displacement 0.000078 0.001200 YES
Predicted change in Energy=-2.059545D-09
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.934 -DE/DX = 0.0 !
! R2 R(1,3) 1.934 -DE/DX = 0.0 !
! R3 R(1,4) 1.9339 -DE/DX = 0.0 !
! A1 A(2,1,3) 120.0001 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0026 -DE/DX = 0.0 !
! A3 A(3,1,4) 119.9973 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
It indicates that our optimisation worked.
Optimised B-Br bond distances: 1.93 Å
Literature reported B-Br bond distances: 1.893 Å[2] (measured via Gas Phase Electron Diffraction)
Optimised Br-B-Br bond angle: 120о
Structure comparison
| Bond type | Optimised bond length | Literature bond length[2] |
|---|---|---|
| B-H | 1.19 Å | 1.19 Å |
| Ga-Br | 2.35 Å | 2.249 Å |
| B-Br | 1.93 Å | 1.893 Å |
We find that, for those two molecules BH3 and BBr3, the optimised bond lengths are close to the experimental determined bond length, and B-Br bond is about 50% longer than B-H bond, which indicates that changing ligand from H to Br results in longer bond length. Both H and Br can form standard two-center, two-electron bond with boron, and they are both more electronegative than boron. But the difference in electronegativity between Br and B is larger than that between H and B, so the B-Br bond is more polar and should be longer.
Another reason is that Br (ground state electronic configuration [Ar]3d104s24p5) has larger and more diffuse valence orbitals than H which only has 1s orbital. When binds to boron (ground state electronic configuration 1s22s22p1), 4p orbital of Br is used to overlap with sp2 hybridized orbital of boron, which results in poor overlap due to a mismatch of size. Compared to H, where 1s orbital is overlapped with sp2 orbital on boron, a good overlap results. So, poor overlap refers to longer and weaker bond. Considering the atomic radii of Br and H, clearly we find Br is much larger than H, so the resulting B-Br bond should be longer.
When changing the center element, from Ga to B, and keeping the ligand unchanged, we find that Ga-Br apparently has a longer bond length than B-Br has. Both can form standard 2c-2e bond as well. But the differences lie in the electronegativity and the ground state electronic configuration. Ga has an electronic configuration of [Ar]3d104s24p1, and 4p-4p overlap is thought to be less good than 4p-2p overlap, so the B-Br bond is shorter. Large atomic radius of Ga can also explain the longer bond length. Besides, Ga has an electronegativity value of 1.81 while boron has a value of 2.04. A more polarized Ga-Br bond is resulted, and this is consistent with the fact that more polarized bond is longer.
In some structures gaussview does not draw in the bonds where we expect, does this mean there is no bond? Why?
No bond is drawn between two atoms doesn't mean that there is actually no bond. Because the bond is drawn based on a distance criteria, so any bond distance longer than this criteria may appear to be no bond in Gaussview.
What is a bond?
Here I define bond as the region between two atoms where electrons are shared or delocalised onto one atom.
Day 4
Frequency analysis of BH3
In order to analyze the frequency, the geometry of BH3 is restricted to D3h.
The complete frequency analysis output file is linked here.
We can find, from below Item part, that the calculation converged.
Item Value Threshold Converged?
Maximum Force 0.000006 0.000450 YES
RMS Force 0.000003 0.000300 YES
Maximum Displacement 0.000023 0.001800 YES
RMS Displacement 0.000012 0.001200 YES
Predicted change in Energy=-2.030890D-10
Optimization completed.
-- Stationary point found.
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
A summary file is reported below:
| File type | .log |
| Calculation type | FREQ |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| E(RB3LYP) | -26.61532363 a.u. |
| RMS Gradient Norm | 0.00000293 a.u. |
| Dipole Moment | 0.00 Debye |
| Point Group | D3h |
| Run time | 5.0 seconds |
And the low frequencies are found to be within plus/minus 15 cm-1 range.
Low frequencies --- -0.9452 -0.8686 -0.0055 5.6959 11.6999 11.7380 Low frequencies --- 1162.9961 1213.1825 1213.1852
Vibrational modes
| No. | Form of vibration | Frequency (cm-1) | Intensity | Symmetry D3h point group |
|---|---|---|---|---|
| 1 |  |
1163 | 93 | A2" |
| 2 |  |
1213 | 14 | E' (degenerate) |
| 3 |  |
1213 | 14 | E' (degenerate) |
| 4 |  |
2582 | 0 | totally symmetric A1' |
| 5 |  |
2715 | 126 | E' (degenerate) |
| 6 |  |
2715 | 126 | E' (degenerate) |
The predicted IR spectrum is shown below:
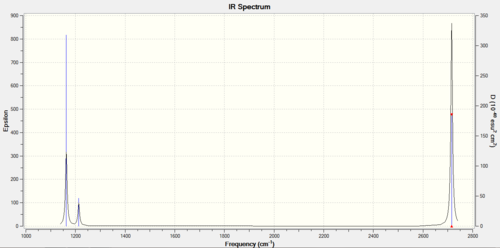
We can find three peaks at 1163 cm-1, 1213 cm-1 and 2715 cm-1. This is in contrast to the fact that there are six vibration modes in total. Because modes 2 and 3 ,5 and 6 are degenerate, they should give the same frequency respectively, and this gives rise to two peaks in our IR spectrum. Another vibration mode at 2582 cm-1 is totally symmetric, i.e. there is no change in dipole moment of the molecule. So, this mode is IR inactive, while other five modes are all IR active.
Frequency Analysis of GaBr3
The output from HPC is: DOI:10042/26114
Summary Information:
| File type | .log |
| Calculation type | FREQ |
| Calculation method | RB3LYP |
| Basis set | LANL2DZ |
| E(RB3LYP) | -41.70082783 a.u. |
| RMS Gradient Norm | 0.00000011 a.u. |
| Dipole Moment | 0.00 Debye |
| Point Group | D3h |
| Run time | 11.8 seconds |
Item information to check if the calculation converged:
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000002 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-6.142863D-13
Optimization completed.
-- Stationary point found.
Low frequencies information:
Low frequencies --- -0.5252 -0.5247 -0.0024 -0.0010 0.0235 1.2010 Low frequencies --- 76.3744 76.3753 99.6982
Lowest real normal mode is 76 cm-1, which represents the lowest vibrational mode.
IR spectrum is included below:
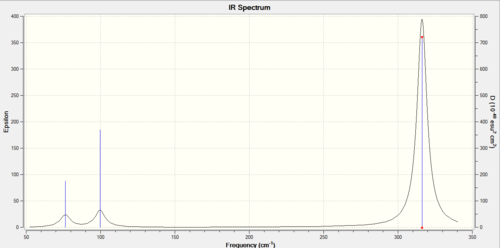
The vibration frequencies of GaBr3 and BH3 are compared:
| No. | BH3 Frequency (cm-1) | BH3 Intensity | BH3 Symmetry D3h point group | No. | GaBr3 Frequency (cm-1) | GaBr3 Intensity | GaBr3 Symmetry D3h point group |
|---|---|---|---|---|---|---|---|
| 1 | 1163 | 93 | A2" | 1 | 76 | 3 | E' (degenerate) |
| 2 | 1213 | 14 | E' (degenerate) | 2 | 76 | 3 | E' (degenerate) |
| 3 | 1213 | 14 | E' (degenerate) | 3 | 100 | 9 | A2" |
| 4 | 2582 | 0 | totally symmetric A1' | 4 | 197 | 0 | totally symmetric A1' |
| 5 | 2715 | 126 | E' (degenerate) | 5 | 316 | 57 | E' (degenerate) |
| 6 | 2715 | 126 | E' (degenerate) | 6 | 316 | 57 | E' (degenerate) |
Generally, from the table above we can see a large frequency difference between each vibrational mode of GaBr3 and BH3. This indicates a much stronger B-H bond, i.e. large force constants, as frequency (in wave number) is proportional to the force constant of vibration. Also, we can find a lower peak intensities for GaBr3 than for BH3, and this infers a lower change in dipole moment of vibrating GaBr3 molecule. Both molecules have D3h point group, so six vibration modes are expected. Among those modes, there are two sets of degenerate modes for each molecule, which give two separate peaks instead of four. Each molecule has one totally symmetric vibration mode, which does not give a peak in IR spectrum.
It is worth noticing that there has been a reordering of modes. In BH3, A2" vibration mode has a lower frequency than that of the two degenerate E' vibration modes. While in GaBr3, the order is opposite. This may be explained by longer Ga-Br bond length.
Both molecules have an IR spectrum of three peaks which corresponds to two degenerate modes and one individual mode. There is a slight difference in peak intensities. The reordering results in shifting of degenerate mode into lower frequencies. Also, we can see that, for both spectra, A2" mode lies closer in energy to E' modes, and A1' mode lies closer in energy to E' modes, but they are higher in energy. This can be explained by different vibration motions. For A2" and the first set of degenerate E', they have specific bending motions, while A1' and the second set of degenerate E' have specific symmetric/asymmetric stretching motions. The stretching motions should have comparable larger force constant than that of bending motions, and this results in higher forces needed in stretching the bonds.
Why must you use the same method and basis set for both the optimisation and frequency analysis calculations?
Because if different basis set and method are used, a large energy difference will be produced and we may get a complete different structure rather than the optimised structure. And this will give us wrong frequencies.
What is the purpose of carrying out a frequency analysis?
To ensure we find the minimal structure and to predict the IR/Raman spectrum of the molecule.
What do the "Low frequencies" represent?
For non-linear molecules, there are totally 3N-6 vibration modes, and low frequencies here represent -6, which are the motions of the center of mass of the molecule.
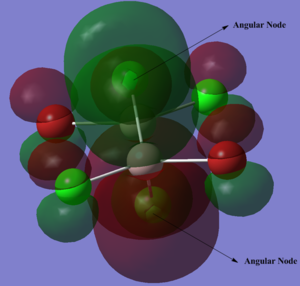
Molecular Orbitals of BH3
HPC output link: DOI:10042/26115
Summary information:
| File type | .log |
| Calculation type | SP |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| E(RB3LYP) | -26.61532360 a.u. |
| Dipole Moment | 0.00 Debye |
| Point Group | CS |
| Run time | 10.2 seconds |
The molecular orbital diagram is shown below:
As I can see, there is a large difference between the real MOs and LCAO MOs, as LCAO only predicts the MOs localised on each atom, while real MO is delocalised into all atoms, i.e. it indicates the electronic distributions. Thus, it appears that real MO is more diffuse than the LCAO MOs. Qualitative MO analysis allows us to have a rough idea of how the orbitals are combined, which is useful when we considering problems involving orbital interactions, but it is not accurate enough to predict the electronic distribution. However, real MOs are able to show us this information.
NBO Analysis of NH3
Geometry optimisation
Output log file is linked here.
| File type | .log |
| Calculation type | FOPT |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| E(RB3LYP) | -56.55776872 a.u. |
| RMS Gradient Norm | 0.00000095 a.u. |
| Dipole Moment | 1.85 Debye |
| Point Group | C1 |
| Run time | 38.0 seconds |
Convergence is checked:
Item Value Threshold Converged?
Maximum Force 0.000002 0.000015 YES
RMS Force 0.000001 0.000010 YES
Maximum Displacement 0.000005 0.000060 YES
RMS Displacement 0.000003 0.000040 YES
Predicted change in Energy=-9.677655D-12
Optimization completed.
-- Stationary point found.
Optimised bond length: 1.02 Å
Optimised H-N-H bond angle: 105.7ο
Frequency analysis
Output file is linked here.
| File type | .log |
| Calculation type | FREQ |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| E(RB3LYP) | -56.55776873 a.u. |
| RMS Gradient Norm | 0.00000131 a.u. |
| Dipole Moment | 1.85 Debye |
| Point Group | C3V |
| Run time | 13.0 seconds |
Convergence check:
Item Value Threshold Converged?
Maximum Force 0.000002 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000006 0.001800 YES
RMS Displacement 0.000003 0.001200 YES
Predicted change in Energy=-1.953916D-11
Optimization completed.
-- Stationary point found.
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Low frequency information:
Low frequencies --- -0.0654 -0.0038 -0.0008 1.3888 4.3127 4.3132
Low frequencies --- 1089.3691 1693.9315 1693.9315
Diagonal vibrational polarizability:
0.1277123 0.1277127 3.3002543
We find that the low frequencies are within the tolerated range.
Population (MO) analysis
Link to output: DOI:10042/26125
Log file is here.
Summary:
| File type | .log |
| Calculation type | SP |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| E(RB3LYP) | -56.55776863 a.u. |
| Dipole Moment | 1.85 Debye |
| Point Group | C3V |
| Run time | 12.3 seconds |
NBO Analysis
Image for charge distribution: (charge range:-1.0 to +1.0)
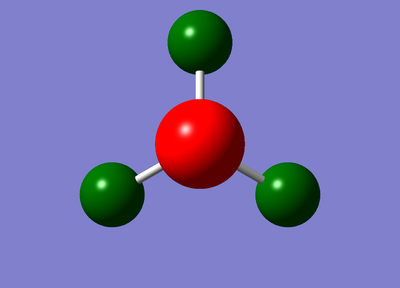
Image fro specific NBO charges for each atom:
The nitrogen has a charge of -1.125 while hydrogen has a charge of 0.375.
Association energies: Ammonia-Borane
Optimisation of ammonia-borane (NH3BH3)
Output file is linked here.
Summary information:
| File type | .log |
| Calculation type | FOPT |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| E(RB3LYP) | -83.22469049 a.u. |
| RMS Gradient Norm | 0.00000168 a.u. |
| Dipole Moment | 5.56 Debye |
| Point Group | C1 |
| Run time | 82.0 seconds |
Convergence check:
Item Value Threshold Converged?
Maximum Force 0.000002 0.000015 YES
RMS Force 0.000001 0.000010 YES
Maximum Displacement 0.000023 0.000060 YES
RMS Displacement 0.000010 0.000040 YES
Predicted change in Energy=-8.925639D-11
Optimization completed.
-- Stationary point found.
Frequency Analysis
Output file is linked here.
Summary information:
| File type | .log |
| Calculation type | FREQ |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| E(RB3LYP) | -83.22468908 a.u. |
| RMS Gradient Norm | 0.00001483 a.u. |
| Dipole Moment | 5.56 Debye |
| Point Group | C3v |
| Run time | 25.0 seconds |
Convergence check:
Item Value Threshold Converged?
Maximum Force 0.000065 0.000450 YES
RMS Force 0.000015 0.000300 YES
Maximum Displacement 0.000175 0.001800 YES
RMS Displacement 0.000060 0.001200 YES
Predicted change in Energy=-8.106389D-09
Optimization completed.
-- Stationary point found.
Low frequencies information:
Low frequencies --- -5.0172 -0.4024 -0.0636 -0.0010 0.8463 0.9843 Low frequencies --- 263.2369 632.8506 638.3695
We find that low frequencies are low, but there is one negative value.
Association Energy
| Molecule | energy in a.u. |
|---|---|
| BH3 | -26.6153236 |
| NH3 | -56.55776872 |
| BH3NH3 | -83.22469049 |
The association energy is calculated via:
ΔEassociation=E(NH3BH3)-[E(NH3)+E(BH3)]= -83.22469049-(-26.6153236-56.55776872)= -0.05159817 a.u.
This refers to an energy of 135.5 kJ/mol. Thus the dissociation energy is +135.5 kJ/mol. This indicates an endothermic dissociation process of ammonia-borane, and the dimer is more stable than the isolated monomers, possibly due to a favorable interaction between lone pair on nitrogen and empty orthogonal empty p orbital on borane, while such interaction does not exist in isolated monomers.
Mini Project: Lewis acids and bases (week 2)
Geometry optimisation
| Name | Isomer 1 | Isomer 2 | Isomer 3 | Isomer 4 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Structure |
|
|
|
| ||||||||||||
| File type | LOG | LOG | LOG | LOG | ||||||||||||
| Calculation Type | FOPT | FOPT | FOPT | FOPT | ||||||||||||
| Calculation Method | RB3LYP | RB3LYP | RB3LYP | RB3LYP | ||||||||||||
| Basis Set | Gen | Gen | Gen | Gen | ||||||||||||
| E(RB3LYP)/ a.u. | -2352.41631610 | -2352.41626680 | -2352.40630792 | -2352.41109945 | ||||||||||||
| RMS Gradient Norm/ a.u. | 0.00001372 | 0.00001283 | 0.00001239 | 0.00002258 | ||||||||||||
| Dipole Moment/ Debye | 0.00 | 0.17 | 0.00 | 0.14 | ||||||||||||
| Calculated Point Group | CS | C2v | C2v | C1 | ||||||||||||
| Real Point Group | C2h | C2v | D2h | C1 | ||||||||||||
| Symmetry element (Click to enlarge) |  |
 |
 |
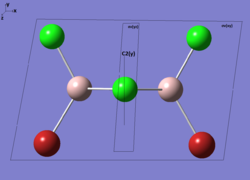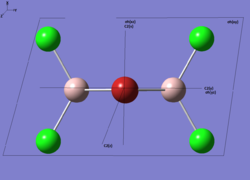C1 | ||||||||||||
| Run Time | 5 minutes 43.7 seconds | 4 minutes 27.4 seconds | 4 minutes 4.1 seconds | 6 minutes 16.5 seconds | ||||||||||||
| Output D-Space Link | DOI:10042/26284 | DOI:10042/26285 | DOI:10042/26286 | DOI:10042/26287 |
Convergence check:
Isomer 1
Item Value Threshold Converged?
Maximum Force 0.000022 0.000450 YES
RMS Force 0.000008 0.000300 YES
Maximum Displacement 0.000916 0.001800 YES
RMS Displacement 0.000483 0.001200 YES
Predicted change in Energy=-1.142040D-08
Optimization completed.
-- Stationary point found.
Isomer 2
Item Value Threshold Converged?
Maximum Force 0.000023 0.000450 YES
RMS Force 0.000008 0.000300 YES
Maximum Displacement 0.000259 0.001800 YES
RMS Displacement 0.000112 0.001200 YES
Predicted change in Energy=-7.122708D-09
Optimization completed.
-- Stationary point found.
Isomer 3
Item Value Threshold Converged?
Maximum Force 0.000041 0.000450 YES
RMS Force 0.000017 0.000300 YES
Maximum Displacement 0.001604 0.001800 YES
RMS Displacement 0.000746 0.001200 YES
Predicted change in Energy=-3.911646D-08
Optimization completed.
-- Stationary point found.
Isomer 4
Item Value Threshold Converged?
Maximum Force 0.000044 0.000450 YES
RMS Force 0.000022 0.000300 YES
Maximum Displacement 0.000876 0.001800 YES
RMS Displacement 0.000376 0.001200 YES
Predicted change in Energy=-6.065827D-08
Optimization completed.
-- Stationary point found.
The energy of each four isomers are reported below in increasing order, and compared with the most stable isomer (as we could find here, the most stable isomer is 1):
| Name | Energy in a.u. | Energy in kJ/mol | Relative energy to Isomer 1 in kJ/mol |
|---|---|---|---|
| Isomer 1 | -2352.41631610 | -6176268.14 | 0 |
| Isomer 2 | -2352.41626680 | -6176268.01 | 0.13 |
| Isomer 4 | -2352.41109945 | -6176254.45 | 13.70 |
| Isomer 3 | -2352.40630792 | -6176241.87 | 26.28 |
The most stable isomer 1 has two terminal Br atoms trans to each other, while for isomer 2, where two terminal Br atoms are cis to each other, energy is slightly higher, and this maybe due to unfavorable flagpole interactions between those two large Br atoms. While isomer 4 has much larger relative energy compared to isomer 1, and isomer 3 has the largest relative energy. The structure indicates that with bridging bromide instead of chloride, energy of the molecule raises significantly. Thus, we observe isomer 3 with 2 bridging bromides, to be the most unstable isomer. The main reason behind this is that Al and Cl atom are in the same period, and their orbitals overlap (3p-3p) is better than the overlaps between Al and Br atom, where bromine 4p orbital has poorer overlap with 3p orbital of Cl. Thus, bridging bromide structure is less favored than the bridging chloride structure, resulting in a more unstable structure and weaker covalent bonding.
Optimisation was also carried out on the corresponding monomer AlBrCl2 in order to find the dissociation energy of our most stable dimer. As before, we use a full basis set 6-31G(d,p) on Al and Cl, and a pseudo potential LANL2DZdp on Br. Result is shown below:
| |||||
| Calculation | Optimisation | Frequency | |||
| File type | .log | .log | |||
| Calculation type | FOPT | FREQ | |||
| Calculation method | RB3LYP | RB3LYP | |||
| Basis set | GEN | GEN | |||
| E(RB3LYP) | -1176.19013697 a.u. | -1176.19013697 a.u. | |||
| RMS Gradient Norm | 0.00000001 a.u. | 0.00000006 a.u. | |||
| Dipole Moment | 0.11 Debye | 0.11 Debye | |||
| Point Group | C2V | C2V | |||
| Run time | 55.6 seconds | 48.1 seconds | |||
| Output Link | DOI:10042/26311 | DOI:10042/26350 | |||
Convergence check:
Item Value Threshold Converged?
Maximum Force 0.000000 0.000015 YES
RMS Force 0.000000 0.000010 YES
Maximum Displacement 0.000000 0.000060 YES
RMS Displacement 0.000000 0.000040 YES
Predicted change in Energy=-1.249277D-15
Optimization completed.
-- Stationary point found.
Low frequencies information:
Low frequencies --- -2.4283 -0.0011 0.0014 0.0024 2.8330 2.9094 Low frequencies --- 120.5195 133.8367 185.7804
It can be observed that we have find the minimal structure.
The association energy of the most stable isomer is calculated via:
ΔE<sub>association</sub>=E(Isomer 1)-2*E(monomer)= -2352.41631610-2*(-1176.19013697)= -0.03604216 a.u.
This corresponds to an energy of -95 kJ/mol. Thus, the corresponding dissociation energy is 95 kJ/mol. A positive dissociation energy indicates that the dissociation process is endothermic, and our dimer is more stable than the two isolated monomers. We can explain this as in monomer, the valence electrons of Al is 6, and this is unfavoured as Al is electron deficient. This electron deficiency can be relieved by accepting one lone pair of another bromide, forming dative covalent bond. Therefore, dimerisation is favored, and the dimer is more stable than the isolated monomers.
Frequency analysis of four isomers
| Name | Isomer 1 | Isomer 2 | Isomer 3 | Isomer 4 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Structure |
|
|
|
| ||||||||||||
| File type | LOG | LOG | LOG | LOG | ||||||||||||
| Calculation Type | FREQ | FREQ | FREQ | FREQ | ||||||||||||
| Calculation Method | RB3LYP | RB3LYP | RB3LYP | RB3LYP | ||||||||||||
| Basis Set | Gen | Gen | Gen | Gen | ||||||||||||
| E(RB3LYP)/ a.u. | -2352.41631610 | -2352.41626680 | -2352.40630792 | -2352.41109945 | ||||||||||||
| RMS Gradient Norm/ a.u. | 0.00001368 | 0.00001281 | 0.00001238 | 0.00002257 | ||||||||||||
| Dipole Moment/ Debye | 0.00 | 0.17 | 0.00 | 0.14 | ||||||||||||
| Calculated Point Group | CS | C2v | C2v | C1 | ||||||||||||
| Run Time | 3 minutes 37.1 seconds | 1 minutes 44.5 seconds | 1 minutes 37.8 seconds | 3 minutes 29.0 seconds | ||||||||||||
| IR Spectrum |  |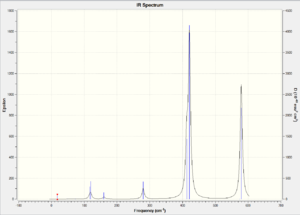
 |
 |
| ||||||||||||
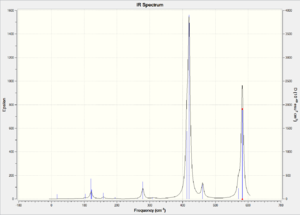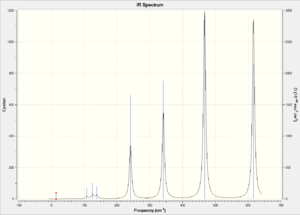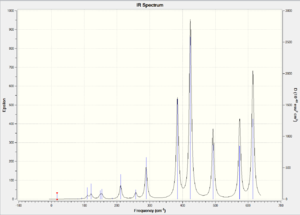
| Output D-Space Link | DOI:10042/26356 | DOI:10042/26358 | DOI:10042/26359 | DOI:10042/26360 |
Convergence check:
| Name | Item information |
|---|---|
| Isomer 1 |
Item Value Threshold Converged?
Maximum Force 0.000040 0.000450 YES
RMS Force 0.000014 0.000300 YES
Maximum Displacement 0.001356 0.001800 YES
RMS Displacement 0.000593 0.001200 YES
Predicted change in Energy=-1.805358D-08
Optimization completed.
-- Stationary point found.
|
| Isomer 2 |
Item Value Threshold Converged?
Maximum Force 0.000032 0.000450 YES
RMS Force 0.000013 0.000300 YES
Maximum Displacement 0.000421 0.001800 YES
RMS Displacement 0.000153 0.001200 YES
Predicted change in Energy=-1.221637D-08
Optimization completed.
-- Stationary point found.
|
| Isomer 3 |
Item Value Threshold Converged?
Maximum Force 0.000026 0.000450 YES
RMS Force 0.000012 0.000300 YES
Maximum Displacement 0.001522 0.001800 YES
RMS Displacement 0.000650 0.001200 YES
Predicted change in Energy=-5.666422D-08
Optimization completed.
-- Stationary point found.
|
| Isomer 4 |
Item Value Threshold Converged?
Maximum Force 0.000049 0.000450 YES
RMS Force 0.000023 0.000300 YES
Maximum Displacement 0.001514 0.001800 YES
RMS Displacement 0.000621 0.001200 YES
Predicted change in Energy=-1.074620D-07
Optimization completed.
-- Stationary point found.
|
And the low frequencies information for each isomer is reported below:
| Name | Low frequencies |
|---|---|
| Isomer 1 |
Low frequencies --- 0.0026 0.0029 0.0045 1.8920 1.9704 3.9624 Low frequencies --- 18.0988 49.0858 72.9223 |
| Isomer 2 |
Low frequencies --- -4.0768 -2.0661 -0.0052 -0.0040 -0.0036 1.4890 Low frequencies --- 17.1900 50.9075 78.5442 |
| Isomer 3 |
Low frequencies --- -5.3391 -5.0240 -3.3016 -0.0036 -0.0011 0.0009 Low frequencies --- 14.7582 63.2903 86.1132 |
| Isomer 4 |
Low frequencies --- -2.4506 0.0022 0.0027 0.0031 0.6077 3.0956 Low frequencies --- 17.0704 55.9280 80.0669 |
Compare isomer 1 with isomer 2, we observe that isomer 2 has more bands in its IR spectrum. Cis and Trans connectivity of Br results in different dipole moment of the molecule. In order for an IR band to be active, the corresponding vibration motion should result in a change in overall dipole moment of the molecule, otherwise it will not appear on the IR spectrum. I have analysed the vibration modes of each isomer, and found that there are 9 IR inactive modes in isomer 1 while there are only 3 in isomer 2. The large difference lies in the molecular dipole moment and point group. As isomer 2 has larger dipole moment than isomer 1, the resulting vibration motions would result in more change in dipole moment and thus more bands in IR.
For isomer 3 and 4, there are 10 IR inactive modes for isomer 3 while all modes are IR active for isomer 4. The difference between those two isomers are the different dipole moment and point group. Isomer 4 is slightly more polar than isomer 3, and it has no symmetry element. Isomer 3 is highly symmetric and nearly non-polar, so it tends to have less IR active vibration modes. Generally, isomer 4 has the most IR active bands while isomer 3 has the least IR active bands.
In order to compare the effect of bridging bromide and terminal bromide on vibration frequency, the following similar modes are compared:
| Isomer | Mode number | Motion | Frequency (cm-1) | Intensity |
|---|---|---|---|---|
| 3 | 11 |  |
197 | 0 |
| 4 | 11 |  |
211 | 21 |
In the first set of modes, bridging bromides stretching mode has lower frequency than bridging plus terminal bromide stretching mode. This can be explained as four weak Al-Br stretchings should result in lower vibration frequency than two Al-Br plus two Al-Cl stretchings. The fact that Al-Br bond is weaker than Al-Cl bond supports this observation.
| Isomer | Mode number | Motion | Frequency (cm-1) | Intensity |
|---|---|---|---|---|
| 4 | 12 |  |
257 | 10 |
| 2 | 13 |  |
309 | 2 |
In the second set of modes, the situation is opposite, as the molecule changed from one terminal bromide to two terminal bromide, and an increase in frequency is observed, indicating a large force constant and overall stronger bonds. Also, the weak Al-Br bond has a lower force constant, and a reordering of mode is occuring.
| Isomer | Mode number | Motion | Frequency (cm-1) | Intensity |
|---|---|---|---|---|
| 3 | 15 |  |
467 | 346 |
| 2 | 15 |  |
420 | 411 |
In the third set of modes, we are comparing the motion of two terminal bromides and two bridging bromides. Surprisingly, the Gaussian analysis indicates two terminal bromides stretchings have lower frequency than two bridging bromide stretchings. This is in contrast with the fact that Al-Br bond is weaker. So I suggest that terminal Al-Br bond is stronger than bridging Al-Br bond because in bridging structure, long pair on bromide is donated to the adjacent Al, lowering the bond order of original Al-Br. Some vibration mixing may occur, and the energy may not be in the same order as expected.
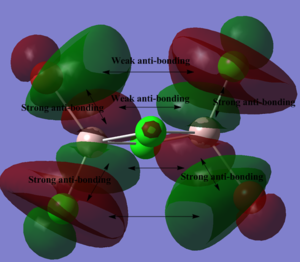
MO analysis of isomer 1
MO calculation summary:
| File type | .log |
| Calculation type | SP |
| Calculation method | RB3LYP |
| Basis set | GEN |
| E(RB3LYP) | -2352.41631610 a.u. |
| Dipole Moment | 0.00 Debye |
| Point Group | CS |
| Run time | 23.9 seconds |
| HPC output | DOI:10042/26450 |
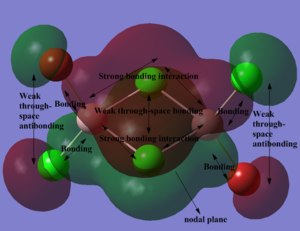
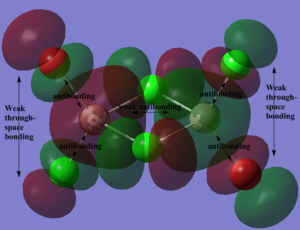
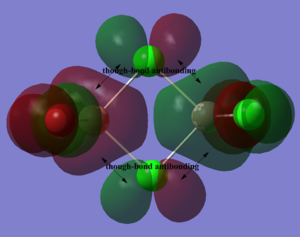
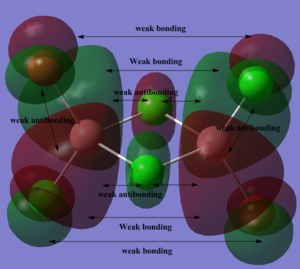
Below, 5 MOs are chosen to analyse, from strongly bonding to strongly antibonding:
| MO number and relative energy | Structure | Analysis |
|---|---|---|
| 43 (-0.40894 a.u.) |  |
This is an overall strongly bonding orbital, with two through-bond strong bonding interactions (terminal Al-Cl and terminal Al-Br) and two through-space weak bonding interactions (in the bridging region). Also AOs from adjacent terminal bromide has weak through-space antibonding interaction as indicated on the diagram. There are generally six angular nodes (nodal planes). |
| 40 (-0.43349 a.u.) |  |
This is an overall strongly bonding orbital. Orthogonal p orbitals on both bridging chlorides and center Al align and overlap together to give a strongly bonding region in the middle of the molecule. Also, p orbitals of terminal halides overlap with p orbitals on center Al in correct orientation resulting in strong through-bond bonding interaction. Only weak through-space antibonding interactions exist between adjacent terminal halides. Generally, it is highly bonding, with a nodal plane in the bridging region. |
| 56 (-0.04770 a.u.) |   |
This is an Overall slightly anti-bonding orbital. As indicated, there are four anti-bonding interactions through the overlap of terminal halide p orbital and s orbital of center Al. And a nodal plane is observed between the anti-bonding region. There are weak anti-bonding interaction between bridging halide and center Al, but due to orientation mis-match, the overlap is not strong. Weak through-space anti-bonding interaction between two Al and weak through-space bonding interaction between adjacent terminal halides exist as well. |
| 57 (-0.03206 a.u.) |   |
This is an overall anti-bonding orbital. Bonding region only exist between two center Al atoms and p orbitals of terminal halides. All these interactions are through-space. Anti-bonding overlaps exist between terminal halides and center Al (through bond), and between bridging chloride and center Al (through space). Considering the relatively high energy of this unoccupied MO, the anti-bonding interaction outweighs the bonding interaction, and the MO is anti-bonding overall. Besides, two angular nodes exist in the bridging chloride, which indicates zero electron density around the center bromide. |
| 69 (0.18323 a.u.) |  |
This is an overall strongly anti-bonding orbital as indicated. Only strong through-bond and weak through-space anti-bonding interaction exist in this MO. Also, I found that this MO is rather delocalised, maybe due to the anti-bonding nature that allowing the electron density spreading around the nucleus. Four nodal planes can be observed. |
References
- ↑ "Physical Constants of Organic Compounds", in CRC Handbook of Chemistry and Physics, Internet Version 2005, David R. Lide, ed., <http://www.hbcpnetbase.com>, CRC Press, Boca Raton, FL, 2005.
- ↑ 2.0 2.1 2.2 W. M. Haynes, D. R. Lide and T. J. Bruno, CRC handbook of chemistry and physics : a ready-reference book of chemical and physical data, 2012, 93, 9–23.