Rep:Mod:zillakilla3
Cope Rearrangement of 1,5-hexadiene
The Cope rearrangment is a [3,3]-sigmatropic shift via a concerted cyclic transition state with either chair or boat conformation.

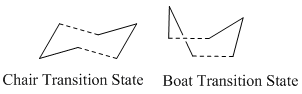 |
Optimisation of the Reactants and Products
1,5-hexadiene can exist as different conformers, each with different energies. Firstly, the anti periplanar conformation was drawn and optimised using the Hartree Fock method, with a basis set 3-21G. The data from the optimisation was collected and is shown below.
| File type | .chk |
| Calculation type | FOPT |
| Calculation method | RHF |
| Basis set | 3-21G |
| Final energy (au) | -231.69253528 |
| Gradient (au) | 0.00001891 |
| Dipole moment (Debye) | 0.0 |
| Point group | Ci |
https://wiki.ch.ic.ac.uk/wiki/images/6/62/ANTI_OPT_1_MR308.LOG
Comparing this with Appendix 1[1] it can be seen that it is Anti 2 conformation: Point Group: Ci Energy: -231.69254 (au)
Secondly the Gauche conformation was optimised, with results below. The expectation is that the Gauche conformer will be less stable than the anti periplanar conformer due to the steric repulsion between the alkene hydrogens.
| File type | .chk |
| Calculation type | FOPT |
| Calculation method | RHF |
| Basis set | 3-21G |
| Final energy (au) | -231.69153032 |
| Gradient (au) | 0.00001866 |
| Dipole moment (Debye) | 0.1281 |
| Point group | C2 |
https://wiki.ch.ic.ac.uk/wiki/images/1/1e/GAUCH_OPT_1_MR308.LOG
Comparing this with Appendix 1 it can be seen that it is Gauche 4 conformation: Point Group: C2 Energy: -231.69153 (au)
This however is not the lowest energy conformation, therefore it was re-drawn and optimised again to yield:
| File type | .chk |
| Calculation type | FOPT |
| Calculation method | RHF |
| Basis set | 3-21G |
| Final energy (au) | -231.69266120 |
| Gradient (au) | 0.00001176 |
| Dipole moment (Debye) | 0.3406 |
| Point group | C1 |
https://wiki.ch.ic.ac.uk/wiki/images/a/ad/GAUCHE3_OPT_1_MR308.LOG
Comparing this with Appendix 1 it can be seen that it is Gauche 3 conformation: Point Group: C1 Energy: -231.69266 (au)
When comparing the two minimised energies, it can be seen that the Gauche conformer is actually lower in energy than the Anti periplanar, which contradicts the previous prediction. This is due to a stereoelectronic effect, where the gauche conformer is stabilised due to interaction between the п C=C orbital and the σ*C-H orbital of the vinyl proton.
The Anti conformer was then optimised further using B3LYP/6-31G* parameters. This agrees well with the literature (appendix 1) energy for the conformer.
https://wiki.ch.ic.ac.uk/wiki/images/b/b6/ANTI_OPT_2_MR308.LOG
Final Energy: -234.61171886 (au) Literature Energy: -234.611710
The geometric differences indicate the changes between the initial optimisation using HF/3-21G and the optimisation using B3LYP/6-31G*. These are shown by the dihedral angles and the bond lengths.
| Basis Set | 1-4-6-9 Dihedral Angle (Degrees) | 4-6-9-12 Dihedral Angle (Degrees) | 6-9-12-14 Dihedral Angle (Degrees) | 1-4/12-14 Bond Length (Angstroms) | 4-6/9-12 Bond Length (Angstroms) | 6-9 Bond Length (Angstroms) |
|---|---|---|---|---|---|---|
| HF/3-21G | 144.67 | 180.0 | 114.67 | 1.32 | 1.51 | 1.55 |
| B3LYP/6-31G* | 118.58 | 180.0 | 118.58 | 1.33 | 1.50 | 1.55 |
| Difference | 3.91 | 0 | 3.91 | 0.01 | 0.01 | 0 |
The difference in energy is 2.92 (au). It can be seen that the second optimisation found a lower energy conformation, indicating that the method used has room for improvement, although a different basis set was used so they cannot really be directly compared. Upon second optimisation the bond lengths slightly decreased, and the bond angles slightly increased, indicating a lengthening of the molecule. This leads to less steric repulsion experienced by the second optimised conformer, and therefore explains the decrease in energy.
Vibrational Analysis
In order to compare the energies a frequency calculation must be carried out. This was done on the B3LYP/6-31G* optimised Anti periplanar conformer. Vibrational and frequency analysis is also carried out as it confirms the molecule is at a minimum on the potential energy surface. The conformation is checked by, after the calculation has completed, opening the real file and checking for to see if it has all converged. The vibrational frequencies are then checked and made sure that they are all positive - any negative frequencies implies a transition state, and any more than one indicates something has gone wrong.
Item Value Threshold Converged? Maximum Force 0.000026 0.000450 YES RMS Force 0.000012 0.000300 YES Maximum Displacement 0.000200 0.001800 YES RMS Displacement 0.000087 0.001200 YES Predicted change in Energy=-1.383693D-08 Optimization completed. -- Stationary point found.
Low frequencies --- -7.0726 -0.0012 -0.0010 -0.0006 7.7047 30.9782
Low frequencies --- 71.0992 80.9667 121.6016
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
AU AU AG
Frequencies -- 71.0992 80.9667 121.4861
Red. masses -- 2.7659 2.6244 2.4776
Frc consts -- 0.0082 0.0101 0.0215
IR Inten -- 0.0275 0.1111 0.0000
These indicate that the frequency analysis was successful and that indeed a minimum was found, due to the convergence and no negative real frequencies.
The thermochemistry data was viewed:
Sum of electronic and zero-point Energies= -234.469184 Sum of electronic and thermal Energies= -234.461835 Sum of electronic and thermal Enthalpies= -234.460891 Sum of electronic and thermal Free Energies= -234.500791
 |
https://wiki.ch.ic.ac.uk/wiki/images/7/76/ANTI2_FREQ_1_MR308.LOG
Optimising the Chair and Boat Transition States
In this section the transition state for the Cope rearrangement of 1,5-hexadiene, consisting of two C3H5 allyl fragments approximately 2.2Å apart. As they are transition states, the frequency analysis will calculate negative frequencies. These can be problematic in the modelling, and therefore there are methods to overcome these issues, explored here.
The allyl fragment was drawn and optimised using HF/3-21G theory level.
Chair Optimisation
TS Berny Method
This optimised fragment was then copied twice to look like the chair conformation transition state. This was then optimised and a frequency analysis run using HF/3-21G.
Viewing the .log file, the convergence and frequencies were viewed:
Item Value Threshold Converged? Maximum Force 0.000145 0.000450 YES RMS Force 0.000040 0.000300 YES Maximum Displacement 0.001501 0.001800 YES RMS Displacement 0.000477 0.001200 YES Predicted change in Energy=-2.949931D-07 Optimization completed. -- Stationary point found.
Low frequencies --- -818.0096 -4.5639 -0.0011 -0.0011 -0.0008 4.2098
Low frequencies --- 10.3140 209.8460 396.5434
****** 1 imaginary frequencies (negative Signs) ******
Diagonal vibrational polarizability:
8.0748592 2.5592261 0.4535566
Diagonal vibrational hyperpolarizability:
-0.0245635 0.0498765 0.0066562
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- -818.0096 209.8460 396.5434
Red. masses -- 9.8928 2.2184 6.7696
Frc consts -- 3.9002 0.0576 0.6272
IR Inten -- 5.9135 1.5796 0.0000
Raman Activ -- 0.0002 0.0000 16.8390
Depolar (P) -- 0.2692 0.6980 0.3881
Depolar (U) -- 0.4242 0.8221 0.5592
The imaginary frequency is of magnitude -818 cm-1, with the vibration as below.
Vibrationjwp108 |
The distance between the carbons was viewed to be 2.01Å. The energy of the optimised structure is: -231.61932218 Hartrees
Frozen Coordinate Method
The previous pasted allyl fragments were opened again, and optimised using a two step process. Firstly the frozen coordinate method was used, by fixing the end carbons at a specific distance (2.2 Angstroms) away from each other.
Low frequencies --- -765.3332 -1.2483 -0.0003 0.0005 0.0007 57.0040
Low frequencies --- 70.5683 201.9266 304.9202
****** 1 imaginary frequencies (negative Signs) ******
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- -765.3332 201.9266 304.9104
Red. masses -- 10.1147 2.3033 6.3212
Frc consts -- 3.4906 0.0553 0.3463
IR Inten -- 0.2652 1.4009 0.0000
Raman Activ -- 0.0002 0.0000 73.8285
Depolar (P) -- 0.2468 0.6248 0.2385
Depolar (U) -- 0.3959 0.7691 0.3852
Vibrationjwp108 |
The bond distances are 2.2 Angstroms, as expected, and the imaginary frequency -765 cm-1. The energy of the optimised transition state is: -231.61518522 Hartrees
This optimised geometry was then run again using the transition state optimisation.
Item Value Threshold Converged? Maximum Force 0.000027 0.000450 YES RMS Force 0.000008 0.000300 YES Maximum Displacement 0.001504 0.001800 YES RMS Displacement 0.000258 0.001200 YES Predicted change in Energy=-4.289620D-07 Optimization completed. -- Stationary point found.
Low frequencies --- -818.0950 -5.2172 -4.2289 -0.0003 0.0001 0.0005
Low frequencies --- 4.2887 209.4919 396.1380
****** 1 imaginary frequencies (negative Signs) ******
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- -818.0950 209.4919 396.1380
Red. masses -- 9.8821 2.2185 6.7574
Frc consts -- 3.8968 0.0574 0.6248
IR Inten -- 5.9202 1.5683 0.0000
Raman Activ -- 0.0000 0.0000 16.8074
Depolar (P) -- 0.6331 0.3510 0.3854
Depolar (U) -- 0.7754 0.5196 0.5564
The negative vibration found was -818 as expected (shown below). The bond distance previously set to 2.2A, is now 2.02A for both C-C breaking/making bonds.
Vibrationjwp108 |
The final energy is: -231.61932205 Hartrees
This energy is different to the previously calculated transition state by such a small amount the discrepancies are probably due to calculation errors. This is supported by the vibrational frequencies being the same, as well as the made/broken bond distance. The downfall of the first method is that the conformation guess must be close to the actual geometry, otherwise the optimisation fails. This is the upside of the second method as the bond distances are set to get a rough approximation of the geometry before the final optimisation.
Boat Optimisation
The boat transition state conformer was modelled using the QST2 method. This is done by inputting the reactants and products, and the calculation will find the transition state between them. This means the numbering of the structures must be the same. Having numbered the atoms correctly the optimisation was set up for transition state optimisation, TS(QST2). This was set up to fail as the boat transition structure would not be found because it would not consider rotation around central bonds. The structures were therefore modified to resemble the boat transition structure more closely. The C-C-C-C dihedral angle was changed to 0o, and the central C-C-C angles were changed to 100o. Upon completion of the calculation the .log file was used to confirm the optimisation had completed.
Item Value Threshold Converged? Maximum Force 0.000033 0.000450 YES RMS Force 0.000012 0.000300 YES Maximum Displacement 0.001549 0.001800 YES RMS Displacement 0.000456 0.001200 YES Predicted change in Energy=-1.339764D-07 Optimization completed. -- Stationary point found.
Low frequencies --- -839.9864 -1.6790 -0.6950 0.0006 0.0007 0.0009
Low frequencies --- 4.4007 155.3832 381.9873
****** 1 imaginary frequencies (negative Signs) ******
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- -839.9864 155.3832 381.9873
Red. masses -- 8.4560 2.2251 5.3927
Frc consts -- 3.5153 0.0317 0.4636
IR Inten -- 1.6110 0.0000 0.0611
Raman Activ -- 27.0412 0.1946 42.2240
Depolar (P) -- 0.7500 0.7500 0.1869
Depolar (U) -- 0.8571 0.8571 0.3150
The imaginary frequency calculated was -840cm-1, shown below, supporting the fact that this is indeed a transition state.
Vibrationjwp108 |
The calculated distance between fragments was: 2.14 Angstroms The energy of the transition state was -231.60280236 Hartrees. The difference between this and the chair transition state is 0.01651969 Hartrees. The chair transition state appears to be lower in energy however the difference is so small, much like the difference between the Anti 2 and Gauche 3 energies, that it is unimportant and could be attributed to calculation differences.
Viewing both the chair and the boat transition states, these can be compared to the Anti 2 and Gauche 3 reactants and products (respectively).
IRC Analysis
Although the boat and chair transition state conformations were optimised it is not possible to predict which conformer they will lead to. As a result the Intrinsic Reaction Coordinate (IRC) method is employed, which follows the minimum energy path from a transition conformation to its minimum on a PES.
The first IRC calculation of the Chair transition structure was calculated using 50 points along the IRC. This calculation did not work as it did not reach a global minimum. After this the force constants were calculated at every step, providing a better result demonstrated by the IRC energy curve reaching a closer minimum.
 |
Final Energy: -231.68513850
 |
Final Energy: -231.69166424
This final energy matches Gauche2 exactly, indicating the chair transition state leads to the formation of the Gauche2 conformer.
The Boat transition state was also subjected to the IRC method, using Calculate Force Constants: Always, and number of steps 75 (to ensure a first time correct analysis). This yielded the following results:
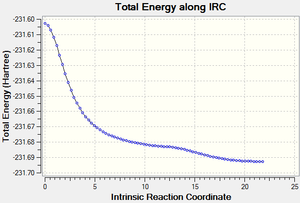 |
Final Energy: -231.69265616
This does not match exactly any of the conformers, and as a result further analysis with more step numbers should be carried out.
The chair and boat transition state geometries were reoptimised using the B3LYP/6-31G* level of theory. These results were compared with the lower basis set optimisations and the anti2 values, and the results shown below.
| HF/3-21G | B3LYP/6-31G* | |||||
|---|---|---|---|---|---|---|
| Electronic energy / a.u. | Sum of Electronic and zero point energies at 0K / a.u. | Sum of Electronic and thermal enthalpies at 298.15K / a.u. | Electronic energy / a.u. | Sum of Electronic and zero point energies at 0K / a.u. | Sum of Electronic and thermal energies at 298.15K / a.u. | |
| Chair Transition State | -231.61932205 | -231.466696 | -231.461337 | -234.55698303 | -234.414930 | -234.409009 |
| Boat Transition State | -231.60280236 | -231.450929 | -231.445301 | -234.54306576 | -234.402355 | -234.396005 |
| Reactant anti2 | -231.692535 | -231.539069 | -231.532565 | -234.611703 | -234.468774 | -234.461856 |
The calculated values match the literature data provided in appendix 1, therefore indicate that the correct structure was in fact found.
Chair Transition State Geometry Data
| Property | HF/3-21G | B3LYP/6-31G* |
| Energy | -231.61932205 (Hartrees) | -234.55698303 (au) |
| C-C-C bond angle (°) | 120.51 | 119.95 |
| Fragments bond distance (Angstroms) | 2.02 | 1.97 |
| C-C bond length (Angstroms) | 1.39 | 1.41 |
| Imaginary frequency (cm-1) | -818 | -566 |
Boat Transition State Geometry Data
| Property | HF/3-21G | B3LYP/6-31G* |
| Energy | -231.60280236 (Hartrees) | -234.54306576(au) |
| C-C-C bond angle (°) | 121.68 | 122.39 |
| Fragments bond distance (Angstroms) | 2.14 | 2.22 |
| C-C bond length (Angstroms) | 1.38 | 1.39 |
| Imaginary frequency (cm-1) | -840 | -526 |
The geometries of the transition states clearly do not change much upon increasing the level of theory, however the energy does decrease upon the reoptimisation indicating a higher level of accuracy in the calculations. This shows the advantages of computing the PES using a low level of theory first, then reoptimising it at a higher level.
The activation energies (below) were calculated from the thermodynamic data and compared with literature. As evident in the results, the activation energy for the chair transition state is lower than for the boat transition state, indicating the reaction pathway that goes through the chair transition state is preferred. This is due to less steric hindrance going via the chair transition state as opposed to the boat transition state.
| HF/3-21G | B3LYP/6-31G* | Experimental Results | |||
|---|---|---|---|---|---|
| at 0K | at 298.15K | at 0K | at 298.15K | at 0K | |
| ΔE Chair | 45.41 | 44.70 | 33.79 | 33.16 | 33.5 +/- 0.05 |
| ΔE Boat | 55.31 | 54.76 | 41.68 | 41.32 | 44.7 +/- 2.0 |
The Diels Alder Cycloaddition
Diels Alder reactions are pericyclic reactions. New σ bonds are formed from the π orbitals of the dienophile and the diene. The number of π electrons determine whether the reactions occur in a concerted stereospecific manner (bond breaking followed by bond forming) or not. Overall, the HOMO/LUMO of one fragment interacts with the corresponding LUMO/HOMO of the other to form two new bonding and anti-bonding molecular orbitals. The simplest Diels-Alder reaction occurs between ethene and cis-butadiene which will be discussed below.
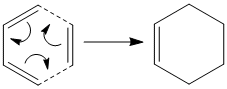 |
Ethene and cis-butadiene were modelled and optimised using the AM1 semi-empirical molecular orbital method, and the HOMO and LUMO MO's were visualised.
| HOMO | LUMO | Energy / a.u. | |
| cis-Butadiene
|
 |
 |
HOMO:-0.343
LUMO:0.017 |
| Ethene
|
 |
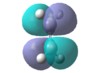 |
HOMO:-0.387
LUMO:0.052 |
Viewing the orbitals and knowing only orbitals of the same symmetry can interact, the HOMO of cis-butadiene will interact with the LUMO of ethene.
To ensure the transition state geometry is successful another optimisation at the higher theory level B3LYP/6-31G was run, and the .log files checked to ensure convergance = YES and the stationary point was found.
Computation of the Transition State Geometry
Having viewed the options of optimising transition states, the TS Berny method is employed. This is because it appeared to yield accurate results with the least problems of the methods employed previously. The transition structure was modelled by creating a bicyclo system and removing one of the C2H4 groups. The bond distances were then edited to 1.5 bonds each, the fragment distance changed to 2.2 Angstroms, and the optimisation run using the HF/3-21G. The structure was then subjected to an optimisation and frequency using the TS Berny method. The .log file was opened upon completion, and the convergence checked, and the vibrations viewed.
Item Value Threshold Converged? Maximum Force 0.000162 0.000450 YES RMS Force 0.000042 0.000300 YES Maximum Displacement 0.001654 0.001800 YES RMS Displacement 0.000683 0.001200 YES Predicted change in Energy=-3.075770D-07 Optimization completed. -- Stationary point found.
Low frequencies --- -818.2627 -9.2983 -6.8519 -5.2675 -0.0003 0.0006
Low frequencies --- 0.0006 166.0615 284.3532
****** 1 imaginary frequencies (negative Signs) ******
Diagonal vibrational polarizability:
3.8813766 2.3475138 1.2188505
Diagonal vibrational hyperpolarizability:
-62.9463596 0.0291174 4.2604045
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- -818.2627 166.0611 284.3532
Red. masses -- 7.0070 2.0103 4.4041
Frc consts -- 2.7642 0.0327 0.2098
IR Inten -- 9.3040 0.6922 1.1477
Raman Activ -- 185.7837 0.1522 5.9196
Depolar (P) -- 0.4422 0.7500 0.7499
Depolar (U) -- 0.6133 0.8571 0.8571
Transition State Energy: -231.60320826
As modelled below, the imaginary vibration occurs at -818cm-1. This indicates the bond formation vibration and the motion is synchronous, suggesting the reaction occurs in a concerted fashion. The lowest real vibration occurs at 166cm-1 and is asynchronous.
Vibrationjwp108 |
| Reactants | Transition state | |
|---|---|---|
| Fragment C-C bond length (Angstroms) | - | 2.21 |
| Ethene C=C bond length (Angstroms) | 1.34 | 1.38 |
| Butadiene C=C bond length (Angstroms) | 1.34 | 1.37 |
| Butadiene C-C bond length (Angstroms) | 1.47 | 1.39 |
| Butadiene C-C=C angle (Degrees) | 127.15 | 121.47 |
The values differ slightly from literature[2] (C-C sp3 1.53 Angstroms, C-C sp2 1.48 Angstroms) however this is expected as the calculations are low level theory, therefore discrepancies are expected. It can be seen that the fragment distance is longer than usual C-C bonds (the Van der Waals radii of Carbons are 1.70 Angstroms[3]), as it is a transition state and therefore the bonds have not fully formed yet. The C-C bond length in cis-butadiene has decreased as it is becoming a double bond, and the C=C bonds have increased in length as they are becoming single bonds.
Also, in the Jmol button it can be seen that the dihedral angle between the carbons and their respective Hydrogens have now decreased, which indicates a transition of the carbons to sp3 hybridised from sp2 hybridisation.
Molecular Orbital Analysis
 |
 |
Both the HOMO and the LUMO show symmetry. Although the HOMO does not give a great deal of information about the reaction, the LUMO does. It appears to form via the interaction between the ethene HOMO and cis-butadiene LUMO (both symmetric). The MO shows to be formed via overlap of the two pi bonds, indicating that in the reaction electron density moves from the ethene to the C-C single bond of cis-butadiene.
Diels-Alder Reaction of Cyclohexa-1,3-diene with Maleic Anhydride
The regioselectivity of the Diels Alder reaction can be studied using this reaction. The major product in this instance is the endo adduct via a kinetically controlled pathway with the endo transition state being lower in energy. By optimising and viewing the transition structures it can be seen if this actually occurs.
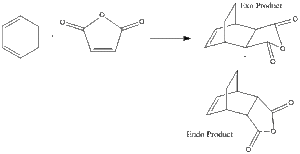 |
Both the endo and exo products were drawn. These were then optimised using semi-empirical AM1 theory, and then altered to look more like the reactants. The double and single bonds involved in the reaction were changed to 1.5 bonds, and the distance between the fragments was changed to 2.2 Angstroms. The optimisation and frequency analysis was then run on both endo and exo adducts, having done so the convergence was checked, yielding the following results.
Exo Adduct
Item Value Threshold Converged? Maximum Force 0.000018 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000284 0.001800 YES RMS Displacement 0.000062 0.001200 YES Predicted change in Energy=-5.370935D-09 Optimization completed. -- Stationary point found.
Low frequencies --- -647.3824 -1.3572 -0.9837 -0.6622 -0.0004 0.0001
Low frequencies --- 0.0007 42.4042 131.4272
****** 1 imaginary frequencies (negative Signs) ******
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- -647.3824 42.4042 131.4272
Red. masses -- 7.8757 4.4549 6.9193
Frc consts -- 1.9447 0.0047 0.0704
IR Inten -- 67.5351 0.5153 0.0051
Raman Activ -- 123.0252 0.4898 3.1649
Depolar (P) -- 0.5615 0.7500 0.7500
Depolar (U) -- 0.7192 0.8571 0.8571
Endo Adduct
Item Value Threshold Converged? Maximum Force 0.000048 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000877 0.001800 YES RMS Displacement 0.000219 0.001200 YES Predicted change in Energy=-1.020110D-08 Optimization completed. -- Stationary point found.
Low frequencies --- -643.3687 -0.5596 -0.0007 -0.0006 0.0004 0.3393
Low frequencies --- 1.1530 64.9637 142.0322
****** 1 imaginary frequencies (negative Signs) ******
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- -643.3687 64.9637 142.0322
Red. masses -- 7.6042 4.1868 7.2207
Frc consts -- 1.8545 0.0104 0.0858
IR Inten -- 36.5470 2.2396 0.6304
Raman Activ -- 83.7294 0.7505 2.3551
Depolar (P) -- 0.5919 0.7500 0.7500
Depolar (U) -- 0.7437 0.8571 0.8571
| Exo | Endo | |||||||
|---|---|---|---|---|---|---|---|---|
| Transition state energy (au) | -605.60359125 | -605.61036822 | ||||||
| Imaginary frequency vibration (cm-1) | -647 | -643 | ||||||
| Imaginary frequency vibration animation |
|
| ||||||
| Lowest real frequency (cm-1) | 42 | 65 | ||||||
| Lowest real frequency vibration animation |
|
| ||||||
| Fragment bond distance (Angstroms) | 2.26 | 2.23 | ||||||
| (C=O)-C-(C=O) through space distance (Angstroms) | 2.289 | 2.294 | ||||||
| C=C distance (Angstroms) | 1.40 | 1.37 | ||||||
| C-C bridge distance (Angstroms) | 1.559 | 1.560 |
NB some distances were written to higher significant figures to illustrate the differences.
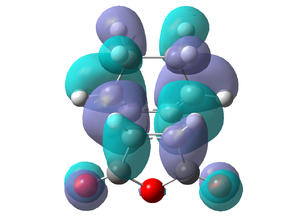
Exo MO's
 |
 |
Endo MO's
 |
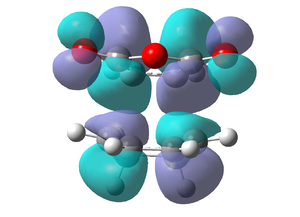 |
It can be seen that the endo transition state is lower in energy than the exo transition state, due to steric hindrance between the cyclohexa-1,3-diene Hydrogens and the maleic anhydride in the exo transition state. There is no steric interactions between the Hydrogens and the maleic anhydride in the endo attack. This supports the fact that the endo isomer is the major product, as it goes by the kinetic pathway via the lower energy endo transition state. The geometry of the transition structures change from their respective starting planar molecules, via a transition from sp2 carbons to sp3 carbons. These are visible on the jmols above. The endo fragment distance is slightly shorter than the exo, which is logical as the steric repulsion will cause a larger fragment distance in the exo transition state, and therefore a slightly longer product C-C bond distance and therefore higher energy.
Both exo and endo HOMO and LUMO's are anti-symmetric. Both HOMO's look similar, and do not show any secondary orbital overlap from the C=O's or C-O-C's - either because there are none in the transition state, or the computational analysis is not sufficient and a higher theory level is needed. The secondary orbital overlap, if there, would stabilise the endo transition state and not be seen in the exo transition state. This involves same phase C=O π*-orbitals of the dienophile interacting with conjugated C=C π-orbitals of the diene (one on each side). Therefore this stabilisation gives the endo transition state a large overlap leading to a greater favourable bonding interaction, where the exo does not have this stabilisation.
Conclusion
As shown in this report computational calculations are very useful in modelling reaction pathways, and deducing which isomer will be the major and minor product. From the data collected thermochemistry can be obtained, and things such as activation energies can be calculated to support the theoretical reaction pathways. The molecular orbital diagrams can indicate which orbitals and bonds are in use going from reactants to products, via the transition states in question. The downfall of these calculations however is the transition structures must be generally known, and the low level theory used will fail if the proposed structures deviate from the actual transition structures. It also does not take into account solvents, although these can be set in a higher level of theory calculation. Overall, for the time period allowed, the calculations were successful in mapping the transition states and therefore able to view the reaction pathways.
References
- ↑ https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3
- ↑ F.H. Allen et. al, J. Chem. Soc., Perkin Trans. 2, 1987, S1-S19: DOI::10.1039/P298700000S1
- ↑ A. Bondi et al, J. Phys. Chem., 1964, 68, 441-451. DOI:10.1021/j100785a001
