Rep:Mod:zg1312

Introduction

A series of transition state was study by using GaussView software in this computational Lab, the transition states of cope rearrangement and Diels Alder reaction between i) cis-butadiene and ethylene ii)cyclohexa-1,3-diene and maleic anhydride were carried out by applying different level of theory include HF/3-21G, semi-empirical/AM1 and B3LYP/6-31Gd. From those calculations, the important chemical property data such as energy, frequency and molecular orbital can be collected and used to analyze the transition states.

In Hartree Fock method, the many-electron wavefunction was obtained by solving selected determinant of single-electron wavefunctions, while the limitation of it is that a general many-electron wavefunction cannot be split as a single determinant. Semi-empirical calculations used the same general structure as Hartree Fock calculation. They both include Hamiltonian and a wave function in calculation, but core electrons are not take account in the calculation and only a minimal basis set is used. Density Functional Theory (DFT) computational method could predict properties of molecules based on electron density of the molecule. ^[1] DFT would give a relatively more accurate value, and B3LYP/6-31G(d) are considered to be used frequently.

Nf710 (talk) 17:25, 17 December 2015 (UTC) they both have their merrits, but good basic understanding

The Cope Rearrangement

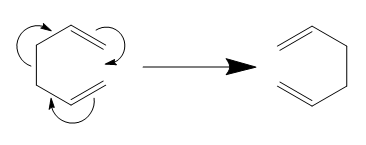
The reaction scheme shown below is [3,3]-sigmatropic rearrangement. A sigma bond was broke while another bond new a sigma bond was formed in the reaction, so total number of σ-bonds and π-bonds remain the same. There are two possible transition states for this reaction which is Chiar and Boat, both of them will be analyzed below.

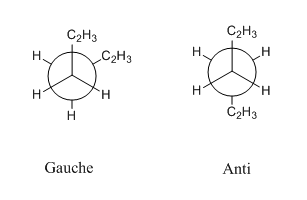
Figure 1. Mechanism of [3,3]-sigmatropic rearrangement

1-5 hexadiene Anti and Gauche structure

The 1-5 hexadiene with anti structure was optimized at the HF/3-21G level theory , then the 1,5-hexadiene with a gauche linkage was optimized through HF/3-21G level theory (Table below shows the results). By comparing both conformers, the gauche conformer are expected to have the higher energy and less favorable. This is because the large -CH=CH2 group which has greater electron density than hydrogen atom in gauche conformer are hinder with each other directly, so the steric strain would be large and rise the energy of the molecule. But -CH=CH2 group in anti conformer are opposite to each other, so the steric strain is smaller.

Figure 2. Newman projection of anti and gauche

However the data of gauche3 conformer actually gives lower energy, and this can be explain by molecular orbital theory. In the highest occupied molecular orbital (HOMO) of gauche3, the π bonding orbital (red orbital in Figure 3) on both -CH=CH2 group are close to each other, so they can interact with each other and could resulting an stabilization effect. But there is not such a interaction in the HOMO of the anti conformer (Figure 4).

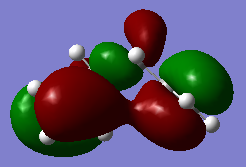
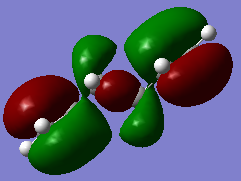
Nf710 (talk) 17:29, 17 December 2015 (UTC) Nice use of MOS to explain the secondary orbital interactions

Anti2 conformation was optimized at both HF/3-21G and B3LYP/6-31Gd level theory. Although the point group of them are both Ci, the small difference in geometry of compound at different level theory was observed. For example i)The bond length of carbon double bond between C9 and C11 of molecule (labelled anti 2 was shown in Table 2.) from B3LYP/6-31Gd(1.333A) is longer than that of molecule from HF/3-21G levels of theory(1.316A). ii)The bond angle of C11-C9-C1(125.3°)in B3LYP/6-31Gd method is larger than the angle at same position(124.8°) in HF/3-21G method. This small difference may because the B3LYP/6-31Gd calculation gives a more accurate value while HF/3-21G calculation is less precise.

Nf710 (talk) 17:30, 17 December 2015 (UTC)This is good but it should be tabulated and it is in the wrong order and you did do the dihedrals

The frequency of anti2 conformation was calculated and there is no imaginary frequency (the frequency with negative value), the relative thermochemistry data can be collected by viewing the file.

Compound	The sum of electronic and zero-point energies(a.u.)	The sum of electronic and thermal energies(a.u.)	The sum of electronic and thermal enthalpies(a.u.)	The sum of electronic and thermal free energies(a.u.)
Anti 2	-234.469219	-234.461869	-234.460925	-234.500809

Table 1. Energy for anti 2

The first one is the potential energy at zero kelvin consist of the energy result from the vibration motion of molecule at 0 K (E = Eelec + ZPE); The second energy is consist of the translational, rotational, and vibrational energy modes at at temperature 298.15 K and pressure 1 atm.; The third one is significant when focusing on dissociation reactions as it include a additional correction for RT (H = E + RT); The last one includes the entropic term which contribution to the gibbs free energy (G = H - TS)

result

Conformer	Energy(Hartrees)	Point Group
Anti	-231.69260	C2
Gauche	-231.69153	C2
Gauche3	-231.69266	C1
Anti2	-231.69254	Ci

Table 2. Result of reactant

Optimization of Chair and Boat Transition Structure

Chair Transition Structure

Optimization of transition state is more complex than minimization, the reaction coordinate (direction of curvature in energy diagram) need take to into consideration during the calculation. There is two ways to optimizing the chair transition structure.

First way is to calculate the force constant matrix (Hessian) at first, then it would updated as optimization process. The transition state need to be speculate reasonably in the input file under this method, otherwise it may cause a failure to compute transition state.

HF/3-21G method was used to optimize an allyl fragment (CH2CHCH2), then a copied allyl fragment was placed 2.2A apart from it in order to make a transition state structure. The whole structure was then optimize (option: TS(Berny) was chose) with calculation of force constant. The frequency calculation gives a imaginary frequency with a magnitude of -818.04 cm-¹. The animation shows when one side of terminal carbon atoms are approaching, while the other side of carbon atoms are getting far away with each other. It is corresponding to the cope rearrangement mechanism (3,3 sigmatropic rearrangement), sigma bond between C6 and C11 (Labelled Chair 1 in Table 3.) is breaking and sigma bond between C3 and C14 is forming.

The imaginary frequency represent the existence of transition state, as the transition state would gives a negative frequency which imply the negative force constant. The calculation of vibration frequency is correlate to the second derivatives; the reaction coordinate diagram shows the transition state is at maximum value where second derivatives gives a negative value. The negative second derivatives value cause the force constant negative which lead a imaginary frequency.

An other way to do the Optimization is freezing the reaction coordinate and minimizing the molecule first, so the molecule can star from some point on the reaction coordinate where possibly closer to the transition state. When the molecule is unfrozen, the calculation start just continue compute alone the reaction coordinate. It is less time consuming as this method is not necessary to compute the whole Hessian.

The same transition structure was copied and both side of terminal atoms were frozened by using redundant coord editor, and it was optimized through HF/3-21G basis set. Then use the redundant coord editor again to unfrozen same position of terminal atoms in optimized molecule, and it was optimized without calculating the force constant.

By comparing the energy from both method (-231.619322 and -231.619232), the energy value is nearly the same which means both way can get an relatively precise chair transition state.

Transition structure	Basis Sets	Energy/a.u.	Point Group
Chair 1	3-21G	-231.619322	C2h
Chair 2	3-21G	-231.619232	C2h
Chair 2	6-31Gd	-234.556931	C2h

Table 3. Result of Chair TS

Boat Transition Structure

QST2 method was used to optimize the boat transition state. The structure of reactant and product was specified at beginning in this method, then the calculation will try to find the transition structure between them. The reactant and product are both 1,5-hexadiene, so it is very important to label the corresponding carbon and hydrogen atoms before and after the reaction in order to obtain the rearranged reactant.

The chk file of anti2 structure from previous part was used in this section. The point group of Anti2 was set to Ci and the molecule was copied twice to two different new slides by selecting add to Molgroup. The original molecule and copied molecule were showed side by side and getting ready for labeling, the number of each atom was edited to the correct order in the atom list. After that, the dihedral angle of central 4 carbons (C2-C3-C4-C5) was changed to 0 degree and inside 3 carbons (C2-C3-C4 and C3-C4-C5) was chaged to 100 degree for both product and reactant. This is in order to distinguish the chair and boat transition state as the calculation would not take consider the possibility of central bond rotation. Finally The file with two structures was calculated by choosing job type Opt+Freq and TS(QST2) option. There is only one imaginary frequency for boat transition state with magnitude -840.22 cm-1.

Nf710 (talk) 17:32, 17 December 2015 (UTC) your frequencies are correct, you should have checked the frequencies of the re optimised structures

Transition structure	Basis Sets	Energy/a.u.	Point Group	Structure
Boat	3-21G	-231.602802	C2v
Boat	6-31Gd	-234.543079	C2v

Table 4. Result of Boat TS

It is hard to predict which transition state would get in the reaction pathway, but intrinsic reaction roordinate (IRC) method could apply to give the energy profile and check the transition state by following the minimum energy path from transition state to the minimum energy level of potential energy surface.

The chair transition state was calculated again by selecting the IRC job type; only forward direction was chose to compute as the this reaction coordinate is symmetrical; the force constants need calculated always at each step along the IRC; 50 number of points alone IRC was used.

When calculation was complete, 44 intermediate geometries was able to observe. But the energy was not reach the minimum value in the energy profile diagram. It may because there is not enough number of point along IRC during the calculation.

Nf710 (talk) 17:35, 17 December 2015 (UTC) You could have done this by re optimizing the final IRC structure

Finally, the vibration energy of both transition structure can be obtain by reoptimizing chair and boat at B3LYP/6-31Gd level theory (where the HF/3-21G for both of them was used as in put file)though the frequency calculation. The electronic energy, sum of electronic and zero-point energies and sum of electronic and thermal energies for both level of theory was list in the table below. Then the activation energy for both transition state can be calculated by finding the difference in energy between transition state and reactant, the result of activation energy was also list in the table below.

There is not much different in their geometry, but the energy different between two level of theory are quite obvious. The number calculated from higher level of theory is closer to the experimental value while the number calculated from lower level of theory diverge from the experimental value about 10 kcal/mol. The data also shows the activation energy of chair transition state is lower the the boat transition state, which means the reaction would probably prefer the chair transition state as less energy required.

Summary of Energy (in hartree)

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619322	-231.466702	-231.461343	-234.556931	-234.414908	-234.408980
Boat TS	-231.602802	-231.450930	-231.445302	-234.543079	-234.402345	-234.396012
*Reactant (Anti2)*	-231.692535	-231.539548	-231.532578	-234.611710	-234.469219	-234.461869

Table 5. Summary of Energy (in hartree)

Result of activation energy (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.71	44.70	34.08	33.19	33.5 ± 0.5
ΔE (Boat)	55.61	54.77	41.96	41.32	44.7 ± 2.0

Table 6.Result of activation energy (in kcal/mol)

Nf710 (talk) 10:43, 18 December 2015 (UTC) Your energies are correct. This is a good wiki you have shown a good level of understanding and have presented it will with the use of jmols. You could have improved it with a greater understanding of the theory.

The Diels Alder Cycloaddition

Diels Alder reaction is a conjugate addition of 4 π-electrons of the diene to 2 π-electrons of the alkene. The reaction between 1. cis-butadiene and ethylene 2. cyclohexa-1,3-diene and maleic anhydride was studied, and the reaction scheme was shown in Figure 6. and 7.

Figure 6.Reaction scheme of butadiene and ethylene

Figure 7. Reaction scheme of cyclohexa-1,3-diene and maleic anhydride

Butadieneand and Ethylene

("Butadieneand" - autocorrect? Tam10 (talk) 11:12, 14 December 2015 (UTC))

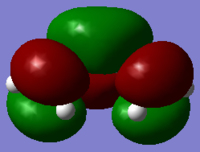
The cis butadieneand and ethylene are optimized by using AM1 semi-empirical molecular orbital method at first followed by B3LYP/6-31Gd method.(Table 7. below shows the results). The HOMO and LUMO can be visualised by GaussView and the symmetry can be obtained with respect to the vertical reflection plane at middle of molecule. The HOMO for cis butadieneand and ethylene is anti-symmetric and symmetric respectively; the LUMO for cis butadieneand and ethylene is symmetric and anti-symmetric respectively. In this case the HOMO of ethylene and LUMO of butadiene can interact with each other, as same applied for LUMO of ethylene and HOMO of butadiene. Therefore, reaction is allowed.

(Use B3LYP/6-31G(d) or B3LYP/6-31*. Not a big issue Tam10 (talk) 11:12, 14 December 2015 (UTC))

	Energy(Hartrees)	Structure	HOMO	LUMO
Cis Butadiene	-155.986485
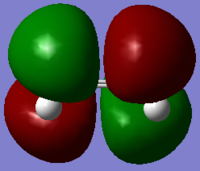
Ethylene	-78.587458

Table 7. Result of Butadieneand and Ethylene

(I don't think B3LYP will produce a minimum for cis-butadiene. What you have is a slightly distorted butadiene. This wouldn't happen with AM1. Tam10 (talk) 11:12, 14 December 2015 (UTC))

A transition state of Diels Alder reaction of butadiene and ethylene was drawn, the terminal carbons of two molecule were set 2.2A apart from each other. Then the transition state was optimized using semi-emperical/AM1 method followed by B3lYP/631Gd method to get the imaginary frequency at -525.07 cm^-1. Then the LUMO and HOMO of this transition state was plotted (as shown below)tells that the HOMO is anti-symmetric and LUMO is symmetric. The distance between C1-C2 (or C3-C4) where the new δC-C bond formed is 2.27 Å; the bond length of C2-C13 (or C3-C11), C1-C4 and C11-C13 is 1.38Å, 1.39Å and 1.41Å receptively; the bond angle of C2-C13-C11 is 122.0 degree. (Labelled TS in Table 8.)

By comparing the reference value: the sp³-sp³ C-C bond length is 1.54 Å, sp²-sp² C-C bond length is 1.47 Å and the van der waals radius of the C atom is 1.85Å.^[2] The partly formed δC-C is longer than sp³-sp³ and sp²-sp² C-C bond length, but it is shorter than 2 Χ van der waals radius (2 Χ 1.85= 3.70Å). This means there is only a bonding interaction between two atoms and it is not strong enough to form a single or double bond.

By looking at the animation of the transition state, two side of terminal atoms are approaching to each other at same time, which means two new bond are forming synchronously. The lowest positive frequency indicate a rotational vibration motion. The butadiene part and ethylene part in TS is rotate in different direction, but the distance between terminal carbons (where the new δ bond formed) does not change a lot. This is different to the vibration at imaginary frequency which terminal carbons vibrate closer to each other and tend to form bond when they are close enough.

	Energy(Hartrees)	Structure	HOMO	LUMO
Ethylene+Cis Butadiene TS	-234.543897

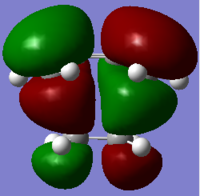
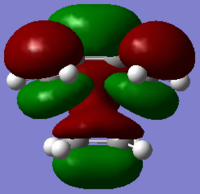
Table 8. Result of Ethylene+Cis Butadiene TS

The HOMO of TS was consist of the HOMO of butadiene (anti-symmetric) and LUMO of ethylene (anti-symmetric), while the LUMO of butadiene and HOMO of ethylene (symmetric) was used to contribute the LUMO of TS (symmetric). They can interact with each other, because the interacting MO are both a or s.

Regioselectivity of the Diels Alder Reaction

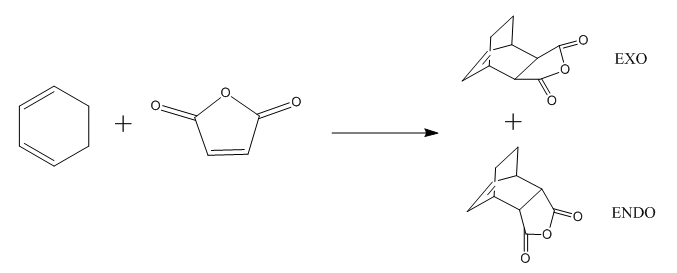
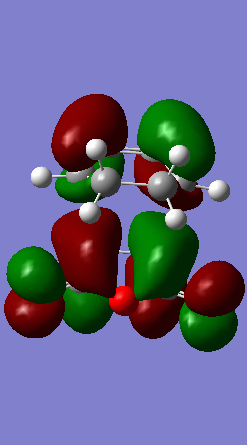
The transition state of Diels Alder reaction between cyclohexa-1,3-diene and maleic anhydride was analyzed in this part, there are two transition state: endo form and exo form. The exo and endo transition state were drew separately and optimized to minimum through semi-empirical/AM1 followed by B3LYP/6-31Gd, then transition state at 6-31Gd level was calculated by changing the option to TS(bemy), finally IRC method was used to find the energy profile of this transition state. The energy profile can give information about the transition state, by looking at the RMS gradient (as Figure 8. and Figure 9. shown below). The gradient increase at first, but it drops to zero afterward. This means the potential energy of reaction molecule reach the maximum (Figure 8. and Figure 9.) at this point where the transition state appears. The reaction was continue, so the RMS gradient increase again to reach the second maximum value and finally goes down towards zero. RMS gradient of both exo and endo got this kind of zero value at middle, so the correct transition state was obtained for both exo and endo.

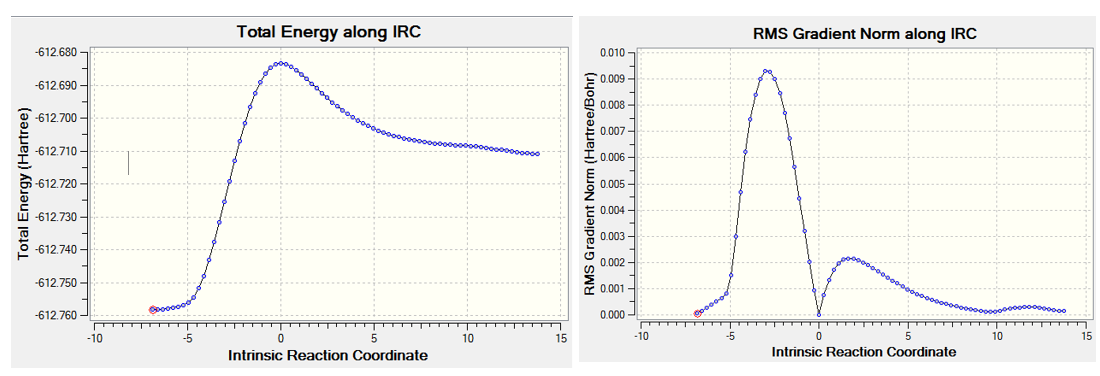
The spatial distance between -(C=O)-O-(C=O)- fragment of the maleic anhydride and -CH2-CH2- fragment for exo and -CH=CH- for endo was measured, the distance is 3.03A and 2.99A respectively. The distance of partly formed σ C-C bonds is 2.29Å for exo and 2.27Å for endo. There is steric effect for exo which may cause it more strained, the distance between C20 and H11 is 2.53Å for exo and distance between C20 and H18 is 3.14Å for endo. The difference between distances may due to the C20-H11 bond in Exo is sp³ hybridized (tetrahedral), so it points toward the carbon on maleic anhydride. The C20-H18 bond in endo was sp² hybridized (trigonal planar), so the H18 will be pointing in the same diction of the plane. (Labelled TS in Table 9)

(Good analysis here. Perhaps put an image of the labeled TS's close by so the reader doesn't have to scroll. Tam10 (talk) 11:12, 14 December 2015 (UTC))

(You write that the differences "may" be due to the hybridisation, when in fact it is definitely due to the hybridisation. Tam10 (talk) 11:12, 14 December 2015 (UTC))

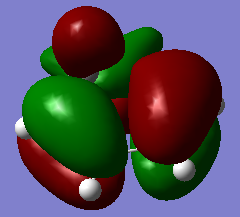
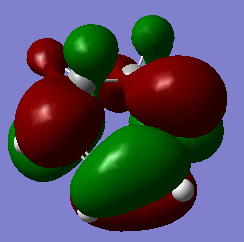
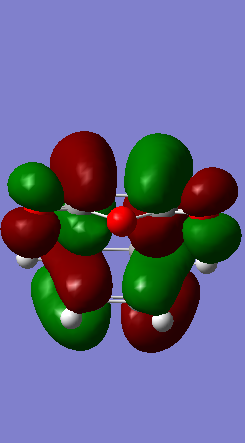
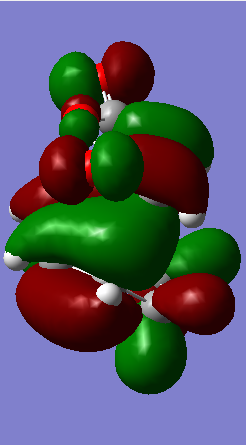
In the pericyclic reaction, the secondary orbital overlap effect means the overlap interaction of a nonactive frame in the frontier molecular orbitals. ^[3] For the HOMO of endo transition state shows in the Figure, the green orbital frame from -(C=O)-O-(C=O)- fragment is very close the other green orbital frame which consist of –CH=CH- fragment below it. This kind of not direct interaction between two double bond component through spacing could considered as secondary orbital overlap. For the exo HOMO(Figure), the -(C=O)-O-(C=O)- fragment is quite far apart from the –CH=CH- fragment as they are located oppositely, so exo TS would not have secondary orbital overlap effect. As secondary overlap can result in lowering energy of transition state.^[4] The endo TS with secondary orbital overlap would have lower energy than exo TS. This means endo TS is under kinetically controlled and it will form faster, which match the experimental value.

(Well answered. It is perhaps a bit difficult to see what you mean from the diagram though. Tam10 (talk) 11:12, 14 December 2015 (UTC))

	Energy (Hartree)	Imaginary frequency (cm^-1)
Maleic Anhydride	-379.289544	/
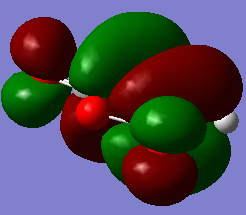
cyclohexa-1,3-diene	-233.418932	/
EXO TS	-612.679310	-448.53
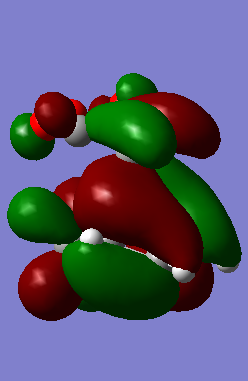
ENDO TS	-612.683396	-446.96

Table 9. Result of cyclohexa-1,3-diene and maleic anhydride Diels Alder Reaction

(These MOs are quite tricky to see. Perhaps use multiple angles, transparency or even jmols. Tam10 (talk) 11:12, 14 December 2015 (UTC))

Conclusion

The transition states for cope rearrangement and diels alder cycloaddition was optimized. Two ways are introduced to get appropriate chair transition state in cope rearrangement, i) direct optimization by computing Hessian first and ii)optimization through freezing the bond. Another method QST2 was used to obtain the both transition state. The first way was chosed to optimize transition state of diels alder reaction and IRC method was applied to check the energy of transition state. Finally, the geometry and energy of transition state was compared with relevant explanation; the HOMO and LUMO of transition state including interaction between molecular orbital(such as secondary orbital overlap effect) was discussed.

Appendix

Reference

↑ Najeeb, Hussein Neama, " Density Functional Theory and Semi-empirical Investigations of Amino Tetrahydrofuran Molecules.", Physics and Materials Chemistry, 2013, 1(2), 21-26.DOI:10.12691/pmc-1-2-3 10.12691/pmc-1-2-3
↑ Fox, Marye Anne; Whitesell, James K. (1995). Organische Chemie: Grundlagen, Mechanismen, Bioorganische Anwendungen. Springer.
↑ M. A. Fox, R. Cardona and N. J. Kiwiet, J. Org. Chem., 1987, 52, 1469–1474DOI:10.1021/jo00384a016 10.1021/jo00384a016
↑ Fleming, Ian (1976) Frontier orbitals and organic chemical reactions

[pmc-1-2-3-1] Najeeb, Hussein Neama, " Density Functional Theory and Semi-empirical Investigations of Amino Tetrahydrofuran Molecules.", Physics and Materials Chemistry, 2013, 1(2), 21-26.DOI:10.12691/pmc-1-2-3 10.12691/pmc-1-2-3

[h-2] Fox, Marye Anne; Whitesell, James K. (1995). Organische Chemie: Grundlagen, Mechanismen, Bioorganische Anwendungen. Springer.

[jo00384a016-3] M. A. Fox, R. Cardona and N. J. Kiwiet, J. Org. Chem., 1987, 52, 1469–1474DOI:10.1021/jo00384a016 10.1021/jo00384a016

[Ian-4] Fleming, Ian (1976) Frontier orbitals and organic chemical reactions

[1]

[2]

[3]

[4]