Rep:Mod:zarfa

Module 3: Transition States and Reactivity

Introduction

The aim of this project is to analyse and characterise the transition states on a potential energy surface (PES) for the Diels-Alder cycloaddition and the Cope Re-arrangement reaction.  This will be achieved by the use of computational chemistry to examine the minimum energy of transition states, reactants and products as well as enhancing our knowledge on the influence of orbital interactions on the energy of the transition states. Increased knowledge of the transition state can influence our understanding of the mechanisms by which reactions proceed, as well the observed rates of reaction amongst other properties.

The computational programes used in this project include GaussView 5.0 and Gaussian. These programes will allow us to model the PES of various molecules by calculating the total energy of the system and will determine the optimal structure of molecules involved in a reaction (using different methods). The optimised molecules can be be further investigated by carrying out frequency calculations.

The focus on this project is on two reactions:

(i) Cope Rearrangement

(ii) Diels-Alder Reaction

Cope Re-arrangement

The Cope re-arrangement reaction named after Arthur Cope, who in 1940 discovered that when a 1,5-diene is heated it undergoes a 3,3-sigmatropic rearrangment into an equivalent but more energitically stable regioisomer. An example shown below: the mechanism is an example of a pericyclic (concerted) reaction, and the transition states in this mechanism can be the chair or boat transition state.

Reaction scheme: The reactant and product in this reaction are isoenergetic and the equilibrium constants for the forward and backward reactions are equivalent.

The reaction can proceed via alternative transition states. The energy of the boat transition state is greater than the chair.

1,5-Hexadiene: Optimisation and Frequency Analysis

The optimisation calculations will give the lowest energy minima and the transition state structures on the PES for the 1,5-hexadiene molecule. The objective of these calculations is to locate the low-energy minima and transition structures on the 1,5-hexadiene potential energy surface in order to determine the reaction mechanism by which the rearrangement proceeds.

1,5-Hexadiene has two preferred conformations it can adopt, these being the anti-peri planar and gauche conformer. The Newman projections of these structures are shown below. The Gaussian programme was used to analyse various conformers that were gauche and anti-peri planar and these were optimised to calculate the minimum energies.

Anti-peri planar and Gauche newman projections

In theory, there are upto 27 isomers of 1,5-hexadiene. 10 of these isomers that have different energies are outlined below. The energies are different for a number of reasons including the orbital overlap, van der Waal's interactions amongst other factors.

Why are the Gauche conformes lower in energy? This is due to the stabilisation provdided by the sigma conjugation. C-H bond donates electron density to other C-H antibonding orbitals.

The following table is taken from Appendix 1

The anti-peri planar and gauche conformers

Gauche Conformers	Pentahelicene	Pentahelicene	Pentahelicene	Pentahelicene	Pentahelicene	Pentahelicene
Energy (Hartrees)	-231.68772	-231.69167	-231.69267	-231.69153	-231.68962	-231.68916
Point group	C2	C2	C1	C2	C1	C1
Anti-peri planar Conformers	Pentahelicene	Pentahelicene	Pentahelicene	Pentahelicene
Energy (Hartrees)	-231.69260	-231.69254	-231.68907	-231.69097
Point group	C2	Ci	C2h	C1

Anti-peri planar conformer

To carry out optimisation calculations different methods can be used. Usually, higher level basis sets (6-31G) compared to lower ones (3-21G) give energies that are similar to literature values.

A 1,5-hexadiene molecule was created on GaussView with an anti-peri planar bond. This molecule was then "Cleaned" and optimised using the following settings: Hartree-Fock method and a 3-21G basis set. Finally, the file was submitted to the HPC server to carry out the calculation.Furthermore, the point group symmetry of the molecule was C_i which indicates there is internal conversion taking place.

The D-space published link can be found here

Optimisation: 1,5-Hexadiene

Anti-peri planar conformer
Point Group	C2
Energy (au)	-231.69260235
RMS Gradient Norm (au)	0.2021
Dipole Moment (Debye)	0.1658
Spin	Singlet
File Name	afrazreactantiouputhpc
File Type	.fch
Calculation Type	FOPT
Calculation Method	RHF
Basis set	321-G

Gauche conformer

To calculate the energy of the gauche conformer, the previous molecule was altered to create a gauche linkage. The same settings were applied as before and again the HPC server was used to carry out the calculations. The point group symmetry is C₁. The D-space published link can be found here The results indicate:

Optimisation: 1,5-Hexadiene

Gauche conformer
Point Group	C2
Energy (au)	-231.68771613
RMS Gradient Norm (au)	0.00001461
Dipole Moment (Debye)	0.4550
Spin	Singlet
File Name	gaucheisomerafrazoutput
File Type	.fch
Calculation Type	FOPT
Calculation Method	RHF
Basis set	3-21G

Gauche energy: -231.68771613 a.u.

Anti energy: -231.69260235 a.u.

The Gauche conformer has a greater energy than the Anti-peri planar conformer. The steric hinderance of the two carbon double bond groups may be the reason for this energy difference. We will investigate the reasons for energy differences in the next section.

The Energy of the different conformers

The energy of different conformers is dictated by stereoelectronic effects. The stereoelectronic effect can be described as an electronic effect that impacts on the structure, properties and reactivity of a molecule. It can be used to relate the electron structure to the geometry of a molecule.

The table below summaries the energies of the different conformers.

The lowest energy conformer is Gauche 3 with C₁ symmetry.

(i) The Van der Waals interactions that exist between the hydrogen atoms are at a maximum

(ii) The Pauli repulsion that exists between neighboring C-H bonds is reduced in this conformation

(iii) Lastly, there is the donation of the electron density from the π_C=C orbital to the σ*_C-H orbital resulting in stabilisation of the bond

Theory suggests the lowest energy conformer is where there is an anti-periplanar relationship between the carbon atoms. However as indicated above the data does not agree with theory.

Optimisation of the C_i anti-peri planar conformer

A 1,5-hexadiene molecule was drawn in GaussView with C_i symmetry. Initially it was optimised using the HF method and 3-21G basis set, this was sent to the HPC server to carry out the calculation. The D-space published link can be found here

Optimisation: 1,5-Hexadiene (3-21G)

Anti-peri planar
Point Group	Ci
Energy (au)	-231.69253516
RMS Gradient Norm (au)	0.000004313
Dipole Moment (Debye)	0.0000
Spin	Singlet
File Name	checkpoint321Ganticonformer
File Type	.fch
Calculation Type	FOPT
Calculation Method	RHF
Basis set	3-21G

After this, a higher level basis set was used: B3LYP method and 6-31G(D) basis set. The higher level basis set should give a more accurate picture of the system The calculation was then run on a HPC server. The D-space published link can be found here

Optimisation: 1,5-Hexadiene 6-31G(D)

Anti-peri planar
Point Group	Ci
Energy (au)	-234.62682247
RMS Gradient Norm (au)	0.00001278
Dipole Moment (Debye)	0.0000
Spin	Singlet
File Name	checkpoint631ganticonfermci
File Type	.fch
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis set	6-31G(D)

The results indicate that when using the higher level basis set, it decreases the energy of the molecule which corresponds to a more stable molecule. Using the 6-31G basis set also gives a value of the energy which is closer to the literature value.. Furthermore, the values of the bond lengths for the C-H and C-C bonds are also slightly different.

Comparison of bond lengths

Bond	3-21G	6-31G
C-C (Å)	1.55	1.56
C=C (Å)	1.32	1.32
C-H (Å)	1.07	1.08

Frequency analysis of the Ci anti-peri planar conformer

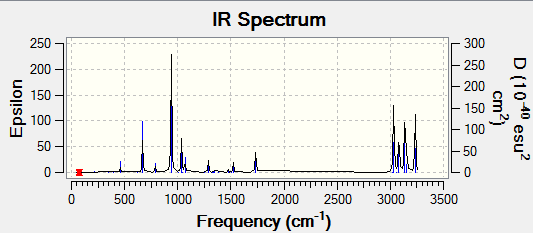
Frequency analysis is an important tool in computational chemistry. Frequency analysis is used to calculate the minimum structure on the potential energy surface and can determine the frequencies of the vibration. If the frequencies have positive values then it corresponds to the minimum however, if one or more of the values are negative it corresponds to the transition state.

Generally, for N number of atoms in a molecule there are usually 3N-6 vibrational modes. For a vibration to result in a peak, there must be a change in the dipole moment of the molecule (hence, must be IR active). Therefore, generally symmetric stretches will not appear on the spectrum. The same method was used in the frequency analysis (6-31G) on the previously optimised molecule. The D-space published link can be found here

Optimisation: 1,5-Hexadiene

Anti-peri planar
Point Group	Ci
Energy (au)	-234.61171032
RMS Gradient Norm (au)	0.00003832
Dipole Moment (Debye)	0.0000
Spin	Singlet
File Name	freq22
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis set	6-31G(D)

 
 Low frequencies ---   -9.5208   -0.0005    0.0004    0.0007    2.8649   11.0477
 Low frequencies ---   74.3242   80.8799  121.4080

Below the IR spectrum indicates that there are 21 vibrational peaks. However, in total there are actually 41 vibrations that occur however for peak to occur on the IR spectrum, it has to be active- there has to be a change in the dipole moment when interacting with an IR wave.

Frequency analysis also gives thermochemical data (which can be used to calculate the activation energy of the transition states).

 
Sum of electronic and zero-point Energies=           -234.469202
 Sum of electronic and thermal Energies=              -234.461855
 Sum of electronic and thermal Enthalpies=            -234.460911
 Sum of electronic and thermal Free Energies=         -234.500777 

	Equation and Values
Property	Equation	Value
Sum of electronic and zero-point Energies	E(0 K) = Eelec + ZPE	-234.469202
Sum of electronic and thermal Energies	E(298.15 K) = E(0 K) + Evib + Erot + Etrans	-234.461855
Sum of electronic and thermal Enthalpies	H = E (298.15K) + RT	-234.460911
Sum of electronic and thermal Free Energies	G = H - TS	-234.500777

Optimization of "Chair" and "Boat" Transition State Structures

This part of the project will focus more on the possible structures for the transition state, specefically the chair and boat structures will be optimised and analysed using various methods.

(i) Method 1: A guess transition structure is drawn and optimised using the "TS Berny" function

(ii) Method 2: This involves freezing the reaction co-ordinate and optimising the rest of the molecule, and then unfreezing and optimising the rest of the structure.

(iii) Method 3: Optimisation using the "QST2" method (does not involve a guess structure) but involves inputting the reactant and product structures to calculate the transition state structure

Method 1: Hessian Method

To create the guess transition state structure for the chair transition state, two allyl fragment (C₃H₅) were created and positioned in a chair transition state like structure (2.20Å distance between the terminal carbons).The results can be found on this link.

Allyl C₃H₅

Allyl
Point Group	C2h
Energy (au)	-115.82303997
RMS Gradient Norm (au)	0.00007172
Dipole Moment (Debye)	0.0291
Spin	Doublet
File Name	allylc3h5logoutputhpc
File Type	.log
Calculation Type	FOPT
Calculation Method	UHF
Basis set	3-21G

After this, the chair transition state was optimised, the job type used was 'Opt +Freq', 'TS (Berny)', the method was HF and the basis set as 3-21G, lastly the keyword chosen was 'opt=noeigen' (prevent the system from stopping if more than one imaginary frequency was detected). here

Optimising Chair Transition State using Method 1

Chair TS
Point Group	C2h
Energy (au)	-231.61932242
RMS Gradient Norm (au)	0.00002672
Dipole Moment (Debye)	0.0002
Spin	Singlet
File Name	chairafraznewguess1outputlog
File Type	.log
Calculation Type	FREQ
Calculation Method	RHF
Basis set	3-21G
Imaginary Freq	1
Vibration

There is a negative vibration (imaginary frequency) at -817.9780 which corresponds to the transition state of the molecule. It essentially confirms the correct formation of the chair transition state.

 Low frequencies --- -817.9780   -3.5381   -1.0455   -0.0006   -0.0005   -0.0005
 Low frequencies ---    1.1751  209.4810  395.9153

Zero-point correction=                           0.152623 (Hartree/Particle)
 Thermal correction to Energy=                    0.157982
 Thermal correction to Enthalpy=                  0.158927
 Thermal correction to Gibbs Free Energy=         0.124116
 Sum of electronic and zero-point Energies=           -231.466700
 Sum of electronic and thermal Energies=              -231.461340
 Sum of electronic and thermal Enthalpies=            -231.460396
 Sum of electronic and thermal Free Energies=         -231.495206

Method 2: Frozen Co-ordinated Method

Frozen Co-ordinate method:

This method was similar to the first in that a guess chair transition state structure was created. The coordinates for the terminal atoms on the allyl fragments that form transition state were fixed to 2.20 Å. The redundant coordinates settings were changed to "Bond" and "Freeze Coordiantes". Furthermore, the structure was then optimised using the HF method and the 3-21G basis set. This avoids the complications of the Hessian method especially in relation to the force constant calculations. There is the imaginary frequency vibration at 817.53 (it is less than the previous method) this is because the bond lengths longer and therefore weaker.

The results can be found on this link

Optimisation of the chair transition state using method 2

Method 2: Frozen Co-ordinated Method
Point Group	C2h
Energy (au)	-231.61509647
RMS Gradient Norm (au)	0.00329468
Dipole Moment (Debye)	0.0013
Spin	Singlet
File Name	logfilefrozenafraz1output
File Type	.log
Calculation Type	FOPT
Calculation Method	RHF
Basis set	3-21G

The second part to this method was to unfreeze the co-ordinates and the change the setting to "Bond" and "Derivative", this essentially optimised the bonds that had been frozen by finding the derivative from the optimised PES. The results are shown: here

Optimisation of the chair transition state using method 2

Method 2: Frozen Co-ordinated Method
Point Group	C2h
Energy (au)	-231.61932178
RMS Gradient Norm (au)	0.00004112
Dipole Moment (Debye)	0.0010
Spin	Singlet
File Name	afterfreezinglogfileoutput
File Type	.log
Calculation Type	FTS
Calculation Method	RHF
Basis set	3-21G

Comparison of method 1 and 2

Bond lengths of terminal atoms (3.d.p): 2.024Å and 2.020Å

Energies: -231.61932242 and -231.61509647

Both methods give very similar data, suggesting both methods are effective in calculating the transition state structures. The advantage of method 2 is that it does not involve the hessian settings and therefore is faster than method 1, and the guess structure does not need to be drawn as accurately for method 2.

Method 3: Boat Transition State (QST2)

In order to optimise the boat transition state, two of the optimised 1,5-hexadienes (anti-peri planar,Ci) were used to represent the reactant and product respectively. The calculation type used was "Opt+Freq" with a "QST2" transition state, the method was HF and basis set set to 3-21G. However, this optimisation failed as the reactant and product geometries were not very similar to the required boat transition state, as the picture below indicates, the method QST2 did not consider the rotation around the central bonds. Thus, the structure is more representative of a chair transition state as it can not find the boat transition state. This method would only work where the reactant and product geometries are identical (or very similar).

The results can be found on this link

Optimisation of the Boat Transition State using Method 3

Boat TS
Point Group	C2v
Energy (au)	-231.61932243
RMS Gradient Norm (au)	0.00002420
Dipole Moment (Debye)	0.0003
Spin	Singlet
File Name	chairafraznewguess1outputlog
File Type	.log
Calculation Type	FREQ
Calculation Method	RHF
Basis set	3-21G
Imaginary Freq	1

In order for the QST2 to work, the geometries of the product and reactant was adjusted by changing the dihedral and bond angles of the central bonds to get the structure more similar to the boat transition state structure. The central C-C-C-C dihedral angle was set to 0° and the inside C-C-C angle was set to 100°.

The results can be found on this link

Low frequencies --- -840.2338   -1.5198   -0.0002    0.0008    0.0020    4.2776
Low frequencies ---    7.9488  155.3839  382.0904

An imaginary frequency was found to occur at -840.2338cm-1 which confirms the formation of the correct boat transition state.

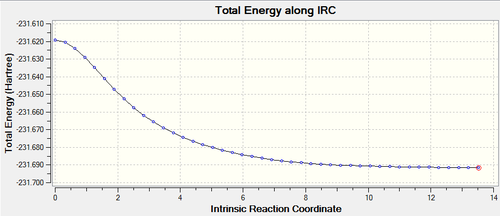
Intrinsic Reaction Coordinate (IRC) Analysis of Chair Transition State

The intrinsic reaction co-ordinate is the minimum energy pathway from the transition state to the reactants or products of a reaction "in mass wieghted cartesian on a PES. An IRC follows the path of a chemical reaction. IRC analysis calculates the local minimum point to the saddle transition state. For example, if one starts at the transition state of a chemical reaction, it can slide down the energy path to the local minimum (reactants or products). IRC analysis can give height of barrier in a reaction and information on thermodynamic properties, reaction rate, etc. This analysis works by continously changing the geometry of the molecule during the reaction. An IRC is used on the optimised chair structure to calculate the 1,5-hexadiene conformer it corresponds to.

Initally, 50 points were taken in the forward direction only. This was similar to the second gauche conformer (in Appendix 1). The results are as follows:

The results can be found on this link

Intrinsic Reaction Co-ordinate

IRC analysis
Energy (au)	-231.61932242
RMS Gradient Norm (au)	0.00002671
Dipole Moment (Debye)	0.0002
Spin	Singlet
File Name	logfileircfirstpart
File Type	.log
Calculation Type	IRC
Vibration

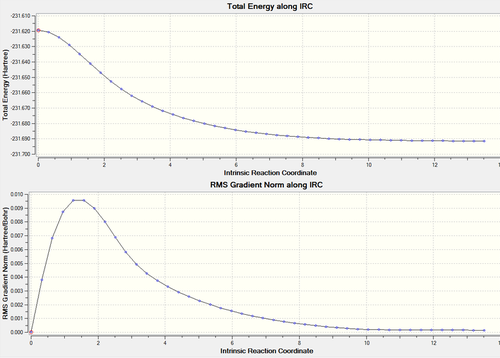
This IRC did not result in the optimised chair conformer, therefore, below a different method was tested and analysed to obtain the optimised chair conformer.

Initially, the IRC failed to reach the optimised geometry using 50 points, therefore the IRC was rerun using a larger range of points, for instance 100 points were used along the IRC. Afterwards, the lowest energy structure was optimised. This is a more effective way of carrying out IRC analysis as the more points used will result in a more accurate picture of the structure.

Lowest energy at -231.69157871 a.u.

The results can be found on this link

Intrinsic Reaction Co-ordinate

IRC analysis Method 2 and 3
Energy (au)	-231.69157871
RMS Gradient Norm (au)	0.00015226
Dipole Moment (Debye)	0.3630
Spin	Singlet
File Name	3rdpartircm2m3
File Type	.log
Calculation Type	IRC
Vibration

Calculation of Boat and Chair Activation Energies

As stated earlier, in the Cope rearrangement reaction of 1,5-hexadiene there are two pathways that go via the chair and boat transition state structures. It is possible to calculate the activation energies for these respective pathways by analysing the structures using a higher basis set of 6-31G(D), as well as carrying out frequency analysis.

Chair Transition State

The results can be found on this link

Chair Activation Energy

Chair
Point Group	C2h
Energy (au)	-234.55698262
RMS Gradient Norm (au)	0.00005027
Dipole Moment (Debye)	0.0001
Spin	Singlet
File Name	logfileoutputoptchairactivationenergy
File Type	.log
Calculation Type	FTS
Calculation Method	RB3LYP
Basis set	6-31G(d)

Item               Value     Threshold  Converged?
 Maximum Force            0.000058     0.000450     YES
 RMS     Force            0.000019     0.000300     YES
 Maximum Displacement     0.000611     0.001800     YES
 RMS     Displacement     0.000155     0.001200     YES
 Predicted change in Energy=-1.196705D-07
 Optimization completed.
    -- Stationary point found.

Frequency Analysis of the Chair Transition State

The results can be found on this link

 Zero-point correction=                           0.142051 (Hartree/Particle)
 Thermal correction to Energy=                    0.147973
 Thermal correction to Enthalpy=                  0.148917
 Thermal correction to Gibbs Free Energy=         0.113165
 Sum of electronic and zero-point Energies=           -234.414932
 Sum of electronic and thermal Energies=              -234.409010
 Sum of electronic and thermal Enthalpies=            -234.408066
 Sum of electronic and thermal Free Energies=         -234.443818

In the second line, the values are positive, these refer to the imaginary frequency and correspond to the presence of the optimimum structure.

 Low frequencies --- -565.6905   -0.0004    0.0007    0.0010   22.0392   27.0711
 Low frequencies ---   40.1427  194.4985  267.7693

Imaginary frequency at -565.6905

Boat Transition State

The results can be found on this link

Boat Activation Energy

Boat
Point Group	C2v
Energy (au)	-234.54309307
RMS Gradient Norm (au)	0.00000403
Dipole Moment (Debye)	0.0613
Spin	Singlet
File Name	logfileoutputboatactivationenergy
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis set	6-31G(d)
Imaginary Freq	1

Item               Value     Threshold  Converged?
 Maximum Force            0.000009     0.000450     YES
 RMS     Force            0.000003     0.000300     YES
 Maximum Displacement     0.000128     0.001800     YES
 RMS     Displacement     0.000052     0.001200     YES
 Predicted change in Energy=-2.676308D-09
 Optimization completed.
    -- Stationary point found.

Frequency analysis of the boat transition state structure. The results can be found on this link

In the second line, the values are positive, these refer to the imaginary frequency and correspond to the presence of the optimimum structure.

 Low frequencies --- -530.3618   -8.3908   -0.0006   -0.0004   -0.0003   15.4632
 Low frequencies ---   17.6137  135.6121  261.7006

The lowest "real" normal mode is found to occur at 135.6121cm-1

Zero-point correction=                           0.140751 (Hartree/Particle)
 Thermal correction to Energy=                    0.147086
 Thermal correction to Enthalpy=                  0.148030
 Thermal correction to Gibbs Free Energy=         0.111341
 Sum of electronic and zero-point Energies=           -234.402342
 Sum of electronic and thermal Energies=              -234.396008
 Sum of electronic and thermal Enthalpies=            -234.395063
 Sum of electronic and thermal Free Energies=         -234.431752

Imaginary frequency at -530.3618

Activation Energies Summary

The energies of the transition states are:

Chair: -234.55698262 a.u.

Boat: -234.54309307 a.u.

The activation energy at 298 K can be determined by calculating the difference between the sums of the electronic and thermal energies of the transition states and product.  Furthermore, activation energy at 0 K can be determined by calculating the difference between the sums of the electronic and zero-point energies of the transition state and reactant.

Activation Energies

Transition State	Activation Energy (6-31G) at 0 K (2 dp)(KCal/mole)	Activation Energy (6-31G) at 298 K (2 dp) (KCal/mole)	Activation Energy (3-21G) at 0 K (2 dp)(KCal/mole)	Activation Energy (3-21G) at 298 K (2 dp) (KCal/mole)	Literature Values
Chair	34.36	33.16	45.72	45.30	33.5 ± 0.5
Boat	41.63	41.07	55.61	50.32	44.7 ± 2.0

Overall, using a higher level basis set during the analysis of the transition states gives us a more accurate picture of the system and especially its energy. The results indicate that the favoured pathway may be the one in which there is a chair transition state due to the lower activation energy.

The reaction may go via a boat transition state structure if the conditions are favourable (thermodynamic conditions) as the system requires thermal energy to mount the barrier. Under kinetic conditions (low temperature) the chair transition state is favoured as it requires less energy to overcome the barrier.

At increased temperatures (289K) the activation energy decreases as the kinetic energy of the molecules increases, compared to lower temperatures (0K).

Finally, the sum of the electronic and zero-point energies of the molecules are lower than the sum of the electronic and thermal energies, this is becuse at 0K there are no thermal vibrations.

The Diels-Alder Cycloaddition Reaction

A Diels-Alder cycloaddition reaction can be described as a "concerted" [4+2] cycloaddition. The reaction involves an alkene dienophile with a conjugated diene, there are also 4n+2 pi electrons which results in a stable cyclic alkene. The Diels-Alder is an interesting and useful reaction due to its stereo-selective and regio-selective properties. The rate of the reaction can be influenced by EWG (increase) on the dienophile (lowers the energy of the pi* orbital so increases the overlap).

A Diels-Alder reaction involves the interaction of the HOMO of one species with the LUMO of another. The two Diels-Alder reactions will be investigated using GaussView and Gaussian in order to determine and analyse the transition state structures and determine the HOMO and LUMO orbitals of the species.

The two Diels-Alder reactions:

(1) ethylene (dienophile) with cis-butadiene (diene)

(2) maleic anhydride (dienophile) with cyclohexa-1,3-diene (diene)

Ethene with Cis-Butadiene

When the ethylene reacts with the cis-butadiene it results in the formation of two sigma bonds between the molecules. The mechanism is shown below:

Mechanism of the reaction between ethylene and cis-butadiene

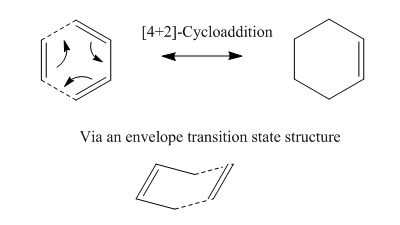
Reactivity is controlled by relative energies of Frontier Molecular Orbitals. The butadiene must be in the cis conformation to enable efficient overlap. The molecular orbitals of the reactants and transition states were determined using Gaussian.

Optimisation of the molecules (butadiene and ethene)

It is important to consider why the reactants form the specific (envelope) transition state structure. Therefore, the molecular orbitals need to be analysed for both ethene and cis-butadiene. These reactants were optimised using a method that was semi-empirical and with a AM1 approach. The results are as following:

Cis-butadiene

The results can be found on this link

Optimisation of Butadiene molecule

Butadiene
Point Group	C2v
Energy (RAM1) (au)	0.04879719
RMS Gradient Norm (au)	0.00001745
Dipole Moment (Debye)	0.0414
Spin	Singlet
File Name	cisbutadieneoutputfile
File Type	.log
Calculation Type	FOPT
Calculation Method	RAM1
Basis set	ZDO

Ethene

The results can be found on this link

Optimisation of Ethene molecule

Ethene
Point Group	D2h
Energy (RAM1) (au)	0.02619043
RMS Gradient Norm (au)	0.00008074
Dipole Moment (Debye)	0.0002
Spin	Singlet
File Name	ethenelogoutputfile
File Type	.log
Calculation Type	FOPT
Calculation Method	RAM1
Basis set	ZDO

The optimisation for both reactants was successful, as indicated by the results RMS gradient values - corresponding to the minimum point on the potential energy surface where the gradient is zero.

Molecular Orbitals

Furthermore, the molecular orbitals were determined using the formatted checkpoint file (FCHK) and are shown below:

Frontier Orbitals of cis-Butadiene and Ethene

Molecular Orbitals	Molecular Orbital Image	Symmetry of the Molecular Orbital	Energy (au)
cis-Butadiene HOMO		Anti-symmetric	-0.34380
cis-Butadiene LUMO		Symmetric	0.01704
Ethene HOMO		Symmetric	-0.38776
Ethene LUMO		Anti-symmetric	0.05283

Cis-butadiene: the HOMO orbital has a node between carbon atom 2 and carbon atom 3. The LUMO has two nodes and is an anti-bonding orbital.

Ethene: the HOMO is a completely bonding orbital (no nodes are present), there is overlap of two p orbitals. The LUMO has one node (anti-bonding orbital).

Diagram shows the frontier orbital for the cis-butadiene and for the ethene molecule.

Ethene MO diagram: 276.47 kCal mol-1 HOMO-LUMO gap

Cis-butadiene MO diagram: 242.68 kCal Mol-1 HOMO-LUMO gap

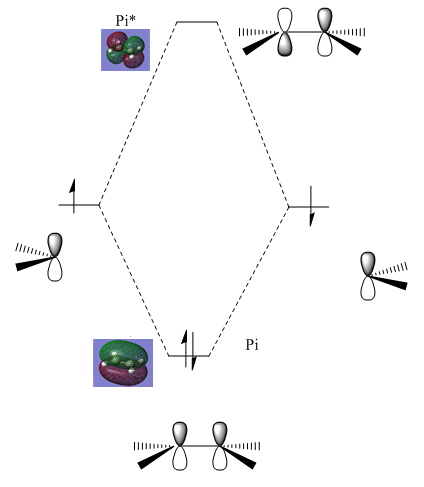
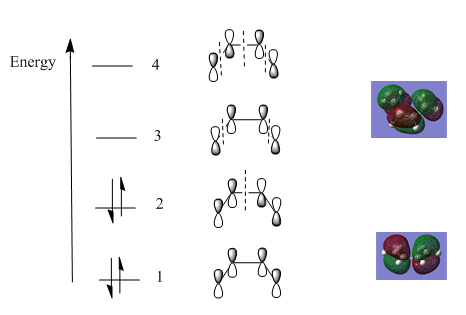
Which orbitals overlap?

For this question, we must consider the symmetry and energy of the frontier orbitals for each molecule. For orbitals to overlap efficiently it is required they have the same symmetry and are similar in terms of energy. Therefore, the HOMO of the cis-butadiene may overlap with the LUMO of the ethene molecule as both are asymmetric. And the HOMO of the ethene may overlap with the LUMO of the cis-butadiene.

Relative energy differences:

(i) 0.40484 a.u.

(ii) 0.39665 a.u.

The value of (i) is greater than(ii) therefore indicating there is stronger overlap of the asymmetric orbitals. This will contribute towards the transition state structure. But energy differences are very close so needs to be investigated further. The MO diagram above indicate that the "real" molecular orbitals are not different from the molecular orbitals formed from the linear combination of atomic orbitals, as a result validating the qualitative MO theory. It proves it can be an accurate tool to model the molecular frame work of simple molecules. MO theory tends to break down when the molecules get more complex and therefore it eventually requires a quantum mechanical description.

Calculation of Optimal Transition State Structures via Frozen Coordinate Method

In this method, the transition state (which is supposed to be an envelope structure), is drawn on GaussView based on a bicycle-2,2,2-octane fragment. The structure was optimised using the semi-empirical AM1 method and using the frozen co-ordinate method. Where the terminal carbons of the transition state were set to 2.20A.

Optimisation

The results can be found on this step 1 link and this step 2 link

Optimisation of the transition state using the frozen co-ordinate method

TS
Point Group	C1
Energy (RAM1) (au)	0.11165465
RMS Gradient Norm (au)	0.00000460
Dipole Moment (Debye)	0.5605
Spin	Singlet
File Name	checkpointfrozenoutput
File Type	.fch
Calculation Type	FREQ
Calculation Method	RAM1
Basis set	ZDO

Frequency analysis

Frequency analysis was also carried out using the same method (semi-empirical AM1). The values indicate the presence of a large imaginary frequency at -935.5938, which corresponds to the formation of the sigma bond and loss of the pi character in the system. The results can be found on this link

 Zero-point correction=                           0.141783 (Hartree/Particle)
 Thermal correction to Energy=                    0.148103
 Thermal correction to Enthalpy=                  0.149048
 Thermal correction to Gibbs Free Energy=         0.112360
 Sum of electronic and zero-point Energies=              0.263447
 Sum of electronic and thermal Energies=                 0.269767
 Sum of electronic and thermal Enthalpies=               0.270711
 Sum of electronic and thermal Free Energies=            0.234024

Low frequencies --- -935.5938 -137.6503  -78.3279  -68.1294   -0.0057   -0.0015
Low frequencies ---    0.0070  142.8641  246.0153

The vibration corresponds to the (pericyclic reaction) formation of the sigmabond and loss of the pi-character. During the reaction, there is a change in the hybdrisation of the ethene molecule from sp2 to sp3. The vibration shows how the ethene molecule interacts with the butadiene and gives an indication of how the HOMO/LUMO orbitals align and interact to form the bonds. The terminal bond length of the transition state is greater than the literature values, indicating that the carbon to carbon bond has not formed. But the length is small enough to suggest that orbital interaction is taking place as the distance is smaller than the van der waals radius of a C atom. 

Lowest frequency real vibration = 142.8641. Corresponds to the twist about the terminal C-C bond

Imaginary frequency at -935.5938. Change of hybrisation: sp2 to sp3

MO Analysis of Envelope Transition State

The molecular orbitals of the envelope transition state are:

Frontier Orbitals of cis-Butadiene and Ethene

Molecular Orbital Image	Energy (au)	Molecular Orbital Comments
	A symmetric orbital with the number of nodes indicating there is weak bonding character. As this MO is symmetric the orbitals that constitute this MO must be antisymmetric. Comprimised of: ethene (LUMO) + butadiene (HOMO)	- 0.32010
	Is antisymmetric with respect to the plane of symmetry and has a greater number of nodes than the HOMO orbital and therefore can be regarded as antibonding orbital. The orbitals that resulted in this MO were symmetric with respect to the plane of symmetry. Comprimised of ethene (HOMO) + butadiene (LUMO)	0.02035

Reaction: Cyclohexadiene and Maleic Anhydride

The second Diels-Alder cycloaddition reaction under investigation is the one between maleic anhydride and cyclohexadiene. The product can be either an exo and/or endo. The exo product is more abundant under thermodynamic conditions, whereas under kinetic conditions the endo product is favoured. This can be explained by considering the influence of orbital interactions in the transition state, and will be under investigation using Gaussian.

The reaction mechanism between cyclohexadiene and maleic anhydride

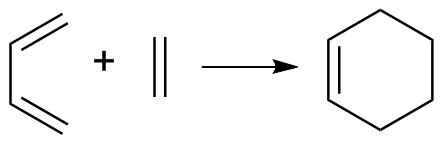
Optimisation of the molecules

Maleic anhydride

The results can be found on this link

Optimisation of Maleic Anhydride

Maleic Anhydride
Point Group	C2v
Energy (au)	-379.28954411
RMS Gradient Norm (au)	0.00011769
Dipole Moment (Debye)	4.0750
Spin	Singlet
File Name	checkpointmaleicanhydrideoutput
File Type	.fch
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis set	6-31G(D)

Cyclohexadiene

The results can be found on this link

Optimisation of Cyclohexadiene

Cyclohexadiene
Point Group	C2v
Energy (au)	-233.41893625
RMS Gradient Norm (au)	0.00003541
Dipole Moment (Debye)	0.3781
Spin	Singlet
File Name	checkpointcyclohexadieneoutput
File Type	.fch
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis set	6-31G(D)

Molecular Orbital Analysis

The Frontier Orbitals of maleic anydride and cyclohexadiene

Molecular Orbital	Molecular Orbital Schematic	Symmetry of MO	Energy (au)
Maleic Anhydride HOMO		Symmetric	-0.29225
Maleic Anhydride LUMO		Anti-symmetric	-0.11710
Cyclohexadiene HOMO		Anti-symmetric	-0.20551
Cyclohexadiene LUMO		Symmetric	-0.01711

The energy gap between the HOMO and LUMO orbitals in maleic anhydride is greater than the one in cyclohexadiene. Maleic anhydride would be able to accept electrons from the HOMO of the cyclohexadiene due to this favourable energy and also because both orbitals are antisymmetric.

The HOMO of the cyclohexadiene molecule has weakly bonding character, it is symmetrical and has a node in the orbital located centrally. The LUMO has a greater number of nodes and therefore can be considered to have greater antibonding character.

The HOMO of the maleic anhydride appears to have strong bonding character, this includes the bonding interactions between the ring and the oxygens. The LUMO has greater antibonding character, which is also suggested by the higher number of nodes on the carbonyl and alkene bonds.

Analysis of Endo and Exo Transition States

The previously optimised molecules were used to create an exo transition state structure. This exo structure was then optimised using the forzen coordinate method using the DFT/6-31(G) level. The terminal carbons were frozen at 2.10 Å.

Exo Transition State

Optimisation The results can be found on this link

Optimisation of the exo transition state

Exo
Point Group	C1
Energy (au)	-612.67931093
RMS Gradient Norm (au)	0.00000958
Dipole Moment (Debye)	5.5508
Spin	Singlet
File Name	exotsopt
File Type	.log
Calculation Type	FTS
Calculation Method	RB3LYP
Basis set	6-31G(d)

Length of bond being formed: 2.17Å

Frequency Analysis

The results can be found on this link

Frequency analysis of the exo transition state

Exo
Point Group	C1
Energy (au)	-612.66055460
RMS Gradient Norm (au)	0.00585287
Dipole Moment (Debye)	5.4480
Spin	Singlet
File Name	exofreqts
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis set	6-31G(d)
Vibration	Imaginary Frequency at 469.6135

(Hartree/Particle)
 Thermal correction to Energy=                    0.190639
 Thermal correction to Enthalpy=                  0.191583
 Thermal correction to Gibbs Free Energy=         0.145270
 Sum of electronic and zero-point Energies=           -612.479719
 Sum of electronic and thermal Energies=              -612.469915
 Sum of electronic and thermal Enthalpies=            -612.468971
 Sum of electronic and thermal Free Energies=         -612.515284

Low frequencies --- -469.6135  -71.0506  -46.0291  -18.2869   -0.0011   -0.0008
Low frequencies ---   -0.0007   28.8459   58.1235

Endo Transition State

Optimisation

The results can be found on this link

Optimisation of the endo transition state

Endo TS
Point Group	C1
Energy (au)	-612.75829019
RMS Gradient Norm (au)	0.00000977
Dipole Moment (Debye)	5.0200
Spin	Singlet
File Name	endoopt
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis set	6-31G(d)

Length of bond being formed: 2.16Å

Frequency Analysis The results can be found on this link

Frequency analysis of the endo transition state

Endo TS
Point Group	C1
Energy (au)	-612.67772252
RMS Gradient Norm (au)	0.00463912
Dipole Moment (Debye)	6.2212
Spin	Singlet
File Name	freqendoanalysis
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis set	6-31G(d)
Vibration	Imaginary Frequency at -476.2820

 Thermal correction to Energy=                    0.191764
 Thermal correction to Enthalpy=                  0.192708
 Thermal correction to Gibbs Free Energy=         0.144448
 Sum of electronic and zero-point Energies=           -612.496507
 Sum of electronic and thermal Energies=              -612.485959
 Sum of electronic and thermal Enthalpies=            -612.485014
 Sum of electronic and thermal Free Energies=         -612.533275

Low frequencies --- -476.2820  -46.1649  -26.6727  -13.5480   -0.0011   -0.0009
Low frequencies ---   -0.0005   46.8498  103.3937

Discussion of Endo and Exo Transition State Structures

It is important to consider the reasons as to why the exo product is favoured under thermodynamic conditions and the endo product under kinetic conditions. Using Guassian and GaussView it enables us to analyse the optimised structures and calculate the activation energies to suggest reasons why the products may be favoured under certain conditions.

Comparison of Transition State Structures (Å)

Parameter	Exo	Endo
Inter-fragment Bond Length (C-C)	2.29	2.27
Bond Length in Maleic (C-C)	1.48	1.48
Average Bond Length in cyclohexadiene (C-C)	1.53	1.54
Bond Length sp2 to sp3 (C-C)	1.40	1.39
Bond Length Former sp3 to sp2 (C=C)	1.40	1.40
Through Space Distance (C=C)-(C-C)	2.96	2.87

The table above displays information on the exo and endo structures, including the bond lengths. It can be seen that both products are very similar. However, there is a small difference in the geometry of the products, especially in the inter-fragment bond lengths (0.02 Å).

Bond Lengths

To explain the differences we also must consider the overall mechanism. The process involves two electrons going from pi bonds to sigma bonds, a new pi bond is also formed on the diene. On the maleic anhydride the C=C converts to a C-C bond (pi to sigma). The double bond that forms in the structures is the same bond length (1.40) in the exo and endo transition state. The C-C bond that forms from the previously C=C bond is also 1.40 in both the endo and exo transition states. Both of these values are different to the literature values, where the C=C is 1.34 A and the C-C is 1.54. More importantly, the product bond lengths are not the same and therefore we cannot define the exo or endo structures as early or late transition states.

Through Space Distances

Although both structures have steric hinderance as both through space distances are smaller than the C-C Van der Waals distance of 3.2 Å. The through space distance is greatest for the exo structure at 2.96 Å compared to the 2.87 Å for the endo transition state structure. Therefore, this suggests there is less steric repulsion between the two molecules in the exo structure. As a result, the exo product is most thermodynamically favoured as they have less repulsive energy.

The endo product is most common in Diels-Alder reactions, suggesting the activation energy for the endo pathway is lower than the exo. The values for the activation energies are given in the table below:

Exo and Endo Activation Energies

Thermodynamic Value	Exo	Endo
Total 'Sum of electronic and thermal energies' for the fragments (maleic anhydride + cyclohexadiene)(au)	-612.53459	-612.53459
Sum of electronic and thermal energies for the transition states (au)	-612.481458	-612.488646
Activation Energy (au))	0.053	0.046
Activation Energy (kCal mol-1) (3 dp)	33.40	28.77

As suggested the activation barrier is smaller for the endo transition state structure than the exo transition state structure. As a result for kinetic conditions, when there is no thermal energy to overcome the exo barrier the endo product will be favoured as it forms the fastest, and there is not enough energy in the system to overcome the activation barrier to go back to the reactants. The greater stability of the endo structure is because of the secondary orbital overlap in the frontier orbitals. Secondary orbital overlap is shown below:

Orbital interactions of the exo and endo transition states

HOMO of Exo

HOMO of Endo

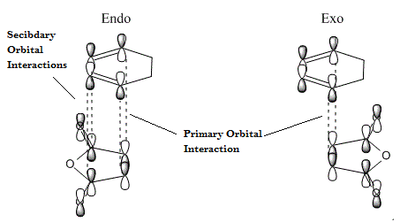
The HOMO of the cyclohexadiene interacts with the LUMO of the maleic anhydride, this makes sense as both orbitals are antisymmetric.

Overall, the exo product has a lower energy than the corresponding endo product due to stabilising interactions in the exo product. However, the endo product pathway has a lower activation energy barrier than the exo.

The HOMO for the endo product has a higher energy because of the repulsive interaction between the π*C=O, these interact with the π*C=C. The exo species has no such repulsive interactions and is the more thermodynamically favoured product.

Conclusion

This project has demonstrated the advantage of using computational chemistry to study transition state structures. It has been shown that using programmes such as Gaussian and GaussView not only can optimise molecules but also allow chemists to study the kinetic and thermodynamic observations in reactions.

Transition state structures are very difficuilt to study using classic scientific techniques. Therefore, by using computational methods it allows chemists to gather optimisation and frequency data from these transition state structures and explain any properties.

In the first part of the project, the Cope Re-arrangement reaction was analysed and it was seen that the reaction proceeded via a chair transition state structure.

In the second part of the project two Diels-Alder reactions were analysed. Firstly, the reaction between ethene and cis-butadiene, this was found to proceed via an enveloped transition state and the reaction was influenced by the frontier molecular orbital interactions. The second reaction was the one between cyclohexadiene and maleic anhydride and it was found that the endo product was favoured over the exo product (in kinetic conditions). This again was due to the orbital interactions that existed.