Rep:Mod:zainphysical
Module 3: The Transition State
The Cope Rearrangement
This module involves the optimisation of 1,5-hexadiene and locate the low energy minima as well the transition state C6H6 during the Cope rearrangement of 1,5-hexadiene. The location of transition state will also help us determine the reaction mechanism. The process proceeds via a six membered ring transition state which exists in two forms. Therefore, the process may proceed a via chair or boat like transition state.
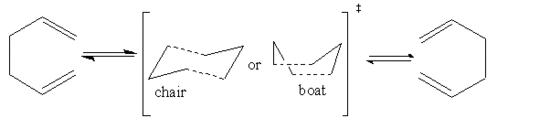
The molecule 1,5-hexadiene exists as several forms of conformational isomers. Some of them were optimised in this module using the HF/3-21G method. Within these conformational isomers, the C-C single bonds may be anti to eachother or gauche in which they would point in the same direction, thus making an angle less than 90o between them.
Optimisation process
Firstly, a conformational isomer of 1,5-hexadiene in which the C-C single bond is anti to eachother was optimised usinf the HF-3-21G method. The optimised molecule is as follows:
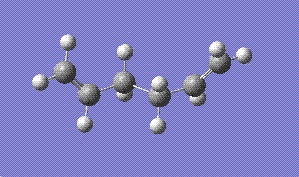
The isomer above was found to have a C2 symmetry and the energy was -231.69260 hartress.
Next, the gauche conformer was optimised using the same method.
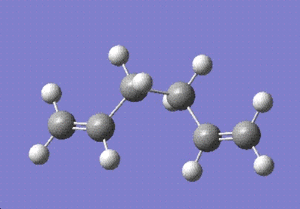
The symmetry was C2 with a minimum energy of -231.69153 hartrees.
The aim now was to find a conformer which has the lowest energy. A guide has been provided in appendix 1 of the script [1]. By comparing our structures with those given in the script and rotating the C=C double bonds around the C-C single bond of the molecule, the lowest energy isomer was found.
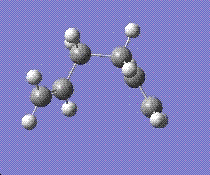
The above conformer had the lowest energy out of all the isomers given in appendix 1 [1], -231.69266 hartress and a C1 symmetry.
Comparing the three structures above with those given in appendix 1, it was found that the first structure optimised in this report matched with anti 1. The energy was found to be exactly the same.
The next structure optimised corresponds to gauche 4 of literature and the lowest energy one is gauche 3 with C1 symmetry.
The Ci anti2 conformation was optimised at the HF/3-21G level. The energy obtained was -231.69254 hartree which is exactly the same as the one given in Appendix 1. The resulting structure was then further optimised using a higher level method, DFT-B3LYP with 6-31G(d) as the basis set.
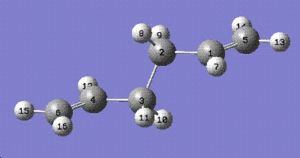
| energy (hartrees) | dihedral angle (C2-C3-C4-C5) | |
|---|---|---|
| HF-3-21G | -231.69254 | 114.7 |
| B3LYP/6-21G(d) | -234.61172 | 118.6 |
The table above shows the difference that is highlighted by the two methods of optimisation used. Although the bond angles and bond lengths have not changed significantly, the dihedral angle and the overall minimum energy has changed a lot.
To be able to compare our values with the ones obtained experimentally, we need to be sure that the structures are at a minimum on the potential energy surface. This can be confirmed by running frequency calculations and analysing the results. The expected results should show all real positive frequencies.
Some useful data has been tabulated below which was extracted from the output file in the visualiser.
| Component | Energy (hartrees) |
|---|---|
| Sum of electronic and zero-point energies | -234.469209 |
| Sum of electronic and thermal energies | -234.461860 |
| Sum of electronic and thermal enthalpies | -234.460916 |
| Sum of electronic and thermal free energies | -234.500791 |
Optimising the Chair and Boat Transition Structures
As discussed earlier, the transition state is important in determining the mechanism of the Cope rearangement. Hence, this section deals with the optimisation of the possible transition states encountered during the course of the reaction.
Initially the allyl fragments (C3H5)of the transition state was optimised at the HF-3-21g level.
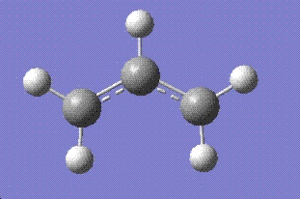
The C-C single bond length is about 1.534 angstroms whereas C=C bond length is approximately 1.332 angstroms[2]. Comparing these with the bond length obtained fro calculations, 1.3886 angstroms, it can be conculded that the bond length represents species which is somewhere in the middle of the two extreme cases, which means it represents a delocalised double bond. This is represented by the dotted lines spread over all three carbon atoms in the allyl structure above.
The chair transition state
The allyl fragment from the previous section was used to generate the chair like trasition state keeping the distnace between the fragments equal to 2.2 angstroms. The resulting chair conformation was then optimised using two different ways; TS-Berny Hartree Fock with 3-21G basis set and the frozen coordinate maethod.
First calculations were run using the HF method setting the optimisation to a TS (Berny) and adding opt=noeigne in additional keywords which would prevent calculations from crashing if more than one imaginary frequency is detected. The results obtained are as follows:
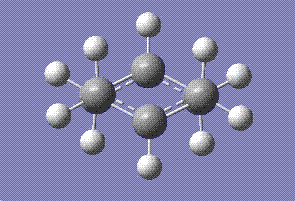
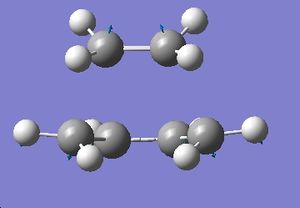
The energy was calcualted as -231.619322 Hartrees and the C-C bond distance between the bonds forming was 2.02 angstroms. The point group was found to be C2h.A negative frequency was observed at -817.94 cm-1. The fact that only one negative frequency is calculated means that we have located the transition state. The calculted frequency also matches well with the obe given in the script, 818 cm-1.This frequency should represent the bond breaking and forming process. Indeed that is observed as shown by the displacement vectors on the following diagram.
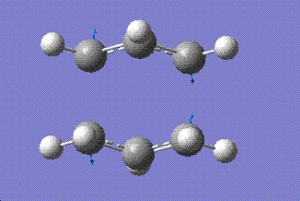
The second method employed was the frozen coordinate method. This utilises the redundant coordinate editor. The C-C bonds on the allyl fragments that join together to make the bond were frozen and the value was set to 2.2 angstroms. The calculations were then run as normal using HF/3-21G method. The results obtained were then run again but this time, a derivative was taken along the bonds that were frozen in the previous calculation.
The energy obatined this time was -231.61932 Hartrees and the imaginary frequency had the value of -817.76 cm-1. This result is in good agreement with those obtained from the HF/3-21G method, thus illustrating the accuracy of both methods and their reliability.
The boat Transition state
The guess structure for the boat like transition state was drawn in a similar fashion as the chair excpet that the guess structure should look like a boat. A new method was used to (QST2) was used to locate the transition state. This methods specifies the reactant and the product for the reaction and the calculation then interpolates between the two structures to locate the transition state.
Initially the dihedral angle between C1-C2-C3-C4 on the reactant molecule and C1-C4-C5-C6 on the product molecule was set to 180o. The calculations failed as the structure did not resemble that of the boat transition state.
The reactant and the product were then drawn with the dihedral angle of 0o and the inside C-C-C bond angle set to 100o in the mol group and labelled as shown in the diagrams below:
Reactant molecule:
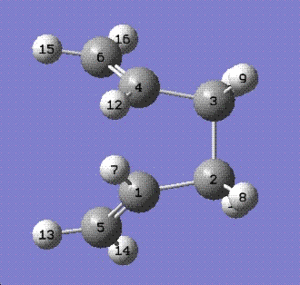
Product molecule:

The final energy came out to be -231.60280 hartrees with a frequency of -840.66cm-1. The point group of the boat transition state was C2V which matches with the one provided in the script.
The objective of this exercise was to prove that an automated technique such as QST2 can also fail if the structures do not closely resemble the transition state.
At this point, the boat transition state was optimised using another technique, QST3 which is very similar to QST2. The difference is that it takes the reactant to product through a different route compared to QST2. Therefore, we would expect to obtain a similar final energy. Indeed that was obtained. The final energy obtained from QST3 is -231.60280 hartrees and a negative frequency of 839.95 cm-1. This value is very similar to the one obtained from QST2.
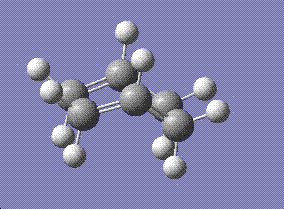
Linking the Transition states to the conformational isomers of 1,5-hexadiene
It is almost impossible to link the transition states calculated in the previous section to any of the conformational isomers of the reactant. Therefore, the method provded by the Gaussian called the Intinsic Reaction Coordinate (IRC) was used to locate a local minima on the potential energy surface. The number of points along the IRC were set to 50 points and the results obtained for the chair conformation is as follows:
The structure above does not look a lot different from the one obtained from earlier calculations. The energy and the RMS gradient plot would tell us if the optimisation process has gone to completion or not.
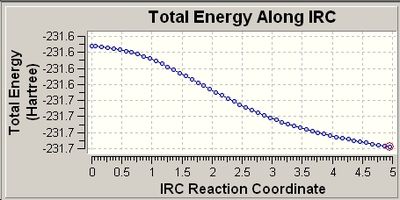
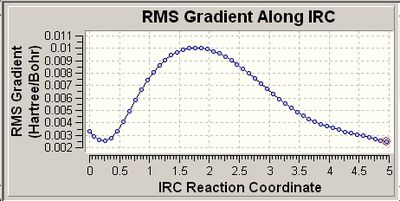
The second graph (RMS) shows that the gradient has not reached minimum or a vaue of zero even after the calcualtions hacve gone to completion. Therefore, the calculations were run again setting to 400 points. This considerably improved the results as shown below:
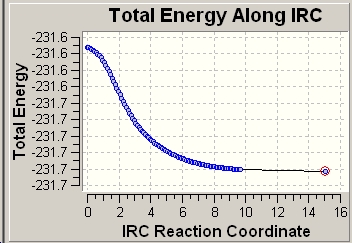

Looking at the RMS curve closely, we can conclude that the optimisation has indeed reached minimum as the RMS curve has hit the zero value. Comparing the structure and the energy obtained (-231.69166 hartrees) with the isomers provided in Appendix 1 [1]. The structure has the same energy as gauche 2 (-231.69167 hartrees).
Gauche 2:
Calculating the Activation Energy
This section involves calculation of the activation energy of the Cope rearrangent if it was to proceed through a chair or boat transition state. Hence, the calculations will enable us to determine the reaction mechanism and whether it proceeds through the more stable chair transition state or not. The procedure for this was to optimise the chair and boat transition states at the B3LYP/6-31G level of theory and then carry out frequency calculations.
| Transition state | Energy B3LYP/6-21G (hartrees) |
|---|---|
| Chair | -234.556983 |
| Boat | -234.543896 |
As the reactant exists as many possible conformations, the one with the lowest energy (Ci) was chosen to calculate the activation energy.
| Chair TS (B3LYP) | Boat TS (B3LYP) | |
|---|---|---|
| Energy (Hartree) | -234.556983 | -234.543896 |
| Energy of reactant (Hartrees) | -234.61172 | -234.61172 |
| Difference in Energy (Hratrees) | 0.05474 | 0.06782 |
| Difference in Energy (Kcal/mol) | 34.35 | 42.56 |
The activation energies calculated above are at 298.15K. Although slightly higher, they match quite well with the literature values obtained from the script. The chair conformation of transition state was found to be more stable as expected by 8.21 kcal/mol.
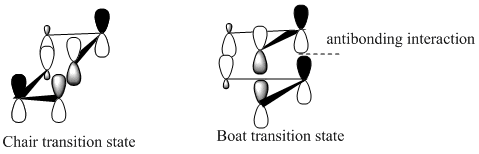
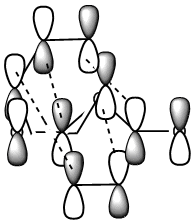
This stability of the chair trnsition state can also be explained in terms of the secondary anti-bonding orbital overlap between the frontier orbitals of the allyl fragments. This happens particulary in the boat transition state and is absent in the chair transition state. This is explained in the book Frontier Orbitals and Organic Chemical Reactions[3]. According to this secondary overlap, the HOMO and LUMO orbitals of the boat transition state interact to produce a destabilising force which is absent in the chair transition state due to a bigger distance between the orbitls concerned (coloured black). This is shown in the diagram below. Another factor is the 1,3 diaxial interactions between the hydrogen atoms in the boat conformation which destabilise it compared to chair conformation.
The activation energies were also calculated at 0K and compared with those give in the script.
| Chair TS | Boat TS | |
|---|---|---|
| Sum of electric and thermal energy (Hartree) | -234.409007 | -234.39681 |
| Energy of reactant (Hartrees) | -234.461863 | -234.461863 |
| Difference in Energy (Hratrees) | 0.052856 | 0.065053 |
| Difference in Energy (Kcal/mol) | 33.17 | 40.82 |
The literature [1] activation energies at 0K are as follows:
| Chair TS | Boat TS | |
|---|---|---|
| Activation energy (kcal/mol) | 31.06 | 41.96 |
| Activation energy (Experimental) | 33.5 ± 0.5 | 44.7 ± 2.0 |
The activation energies calculated at 0K agree with both the experimental and computational results given in the script. Agreement with the experimental values show that computational methods such as B3LYP/6-31G are quite accurate. However, more accurate results results can be obtained from computational methods simply by using a more accurate method and using a better basis set.
The Diels Alder reaction
The Diels alder reaction belongs to the class of pericyclic reactions. The reaction under consideration in this section is the famous [4+2] cycloaddition reaction between ethene and cis-butadiene. The π orbitals of the diene react with the σ orbitals the dienophile according to the reaction below. Since both the reactants do not bear any substituents, we will not concentrate on the selectivity issues such as endo or exo selectivity in this section. Apart from locating the transition state of the reaction, moleuclar orbitals were also calcualted to give a clear idea of the mechanism of the reaction and to verify which of the reactant's HOMO orbitals participate with the other's LUMO orbitals.

Inorder, for the orbitrals for both adducts to overlap, they should share the same symmetry. Hence a full analysis of molecular orbitals has been done to find out which overlap is allowed or disallowed. Both reactants were optimised using the semi-empirical AM1 method. The molecular orbitals are as follows:
| Butadiene HOMO | Butadiene LUMO | Ethene HOMO | Ethene LUMO | |
|---|---|---|---|---|
| Qualitative MO's |  |
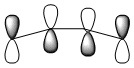 |
 |
 |
| Quantitavie MO's | 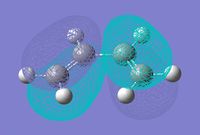 |
 |
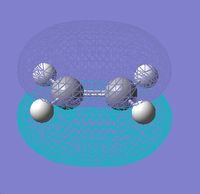 |
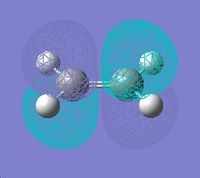 |
| Symmetry | antisymmetric | symmetric | symmetric | antisymmetric |
The qualitative orbitals drawn for both reactants match really well with the quantitative orbitals. The orbitals calculated from the technique also shows the relationship between the HOMO of one reactant with the LUMO of another which is neccessary for the reaction to proceed as mentioned earlier. The HOMO orbital of ethene is symmetric and will only react with the symmetric LUMO orbital of butadiene. Likewise, this is true for the other set of frontier orbiatals.
The optimised structures from above were then used to generate a guess structure for the transition state, placing both the reactants in such way that they resemble the transition state's structure. This was then optimised using the redundant coordinate editor method in which the two carbon atoms of both reactants are frozen and a derivative is taken along them. Finally, the transition structure was optimised to give optimum results using the more accurate DFT/6-31G(d) method as AM1 is less accurate and does not take the electrons into account.
The C-C bonds forming were calculated to be 2.273 angstroms apart. This indicates that the bond forming process is synchronus. The following table gives the literature value of sp2 and sp3 C-C bond lengths.
| C-C sp3 bond length/Ã[2] | C-C sp2 bond length/Ã[2] | Van der Waals radius/Ã[2] |
|---|---|---|
| 1.54 | 1.38 | 1.70 |
A transition state can never be seen or isolated. Therefore, the transition state of a reaction contains bonds that are not fully formed during the course of a reacion. This is demonstrated in this example. The Van der Waals radius of a carbon atoms is the radius of a free carbon atom. Twice this distance (3.40)Ãgives the value of two isolated carbon atoms placed together. The distance mentioned above (2.273Ã) is a lot less than 3.40Ã, therefore suggesting some kind of overlap between the two reactants. Since this value is bigger than 1.38Ã, it can be deduced that the C-C bond has not been fully formed in the transition structure.
The frequencies were also calculated. Only one negative frequency was obtained at 523.87 cm-1 which shows that we have arrived at the transition state. If we look closely at the wave vectors displayed in the diagram and the motion of vibration of the imaginary frequency, the vibration corresponds to the reaction path at the transition state.
The frontier orbitals and their symmetry was also computed and the results from AM-1 are displayed as follows:
| HOMO-1 | HOMO | LUMO | |
|---|---|---|---|
| Orbitals | 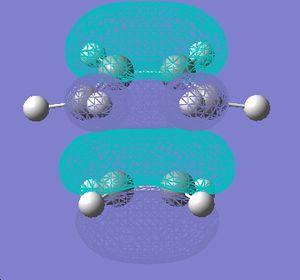 |
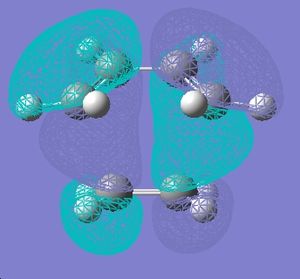 |
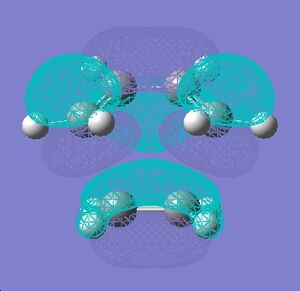 |
| Symmetry | Symmetric | Antisymmetric | Symmetric |
| Energy (a.u) | -0.325 | -0.323 | 0.023 |
As mentioned earlier, the frontier orbitals of the interacting reactants should share the same symmetry. Once the reaction happens, the resulting orbital formed should also have the same symmetry. The HOMO of the transition state calculated is antisymmetric, therefore it has been formed as result of mixing of two antisymmetrical orbitals. Hence, it can be concluded that the HOMO of butadiene (antisymmetric) reacts with the LUMO of ethene (antisymmetric).
Since, the calcualtions were repeated with a more accurate technique, B3LYP, it was a wise decision to generate the frontier orbitals obtained from B3LYP. An interesting thing to notice was that the HOMO and HOMO -1 obtained from AM1 had been swoped over. Hence, their energies were added in the table which are very similar in magnitude.
Therefore, it is almost impossible to tell accuartely which of the HOMO or LUMO orbitals of each reactant for the HOMO orbital of the product.
The orbitals from B3LYP have been tabulated below:
| HOMO | LUMO | ||
|---|---|---|---|
| Orbitals | 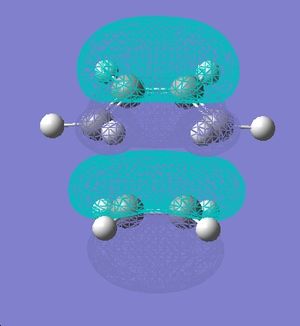 |
 | |
| Symmetry | Symmetric | Symmetric |
The pericyclic reactions proceed according to a selection rule which states that aromatic systems containing 4n+2 electrons proceed via a Huckel transition state and the overlap of the orbitals takes place suprafacially, hence, no twisting of the orbitals is required. This suprafacial overlap has been shown in this example which contains 6 п electrons and therefore satisfies the 4n+2 condition. Hence, the reaction is allowed.
The activation energy of the Diels alder reaction was also calcualted as follows:
| Combined energy of reactants (Hartrees) | -234.57341 |
|---|---|
| Energy of transition state (Hartrees) | -234.54390 |
| Activation energy (Hartrees) | 0.02951 |
| Activation energy (Kcal/mol) | 18.52 |
The reaction of Maleic Anhydride and Cyclohexa-1,3-diene
This section involves the study of reaction of Maleic anhydride and cyclohexa-1,3-diene. The reaction is again an example of a [4+2] cycloaddition reaction, similar to previous section, but the dieneophile has attached to it electron withdrawing substituents hence, it is electron deficient. This reaction can give two possible products, exo or endo product. In the endo product the substituents on the dieneophile point away from the diene. However, opposite is true for the exo product. An attempt would be made using computational methods to prove that endo product is more stable than exo as predicted by the so called endo rule. According to this rule, the endo product is more stable product and is therefore produced in excess.

The optimisation process for this section was the same as the one used for Dield Alder reaction. Initially the reactants were optimised using the semi empirical formulae (AM1), the transition state was predicted from these optimised structures and finally to obatain accurate results, B3LYP/6-321G method was used. The results are tabulated below:
| Transition state | Structures | Energy (Hartrees) | Frequency | ||
|---|---|---|---|---|---|
| Endo | -612.6833968 | -446.8 | |||
| Exo | -612.6793110 | -448.1 |
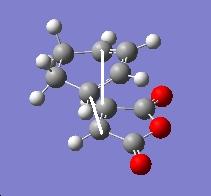
First thing to look at from the results above is the frequency for each transition state. A negative value for each confirms that we have reached and located a transition state. The motion was also viewed and was observed to represent the bond forming between the carbon atoms of the two reactants in a synchronous manner. Secondly, comparison of the relative energies of exo and endo confirm that the endo transition state is indeed lower in energy and hence more stable than exo, therefore, promoting the endo product. This selectivity can also be explained in terms of the enhanced bonding interactions present in endo state only marked by the dotted lines in the figure below[3]. In exo, the distance between the two fragments in the transition state is simply too large for any of these interactions to exist as will be proved later.
The important C-C bond distances obtained from each transition state are tabulated below;
Endo transition state:
| Sketch of the C-C bond | Distance (angtroms) |
|---|---|
 |
2.269 |
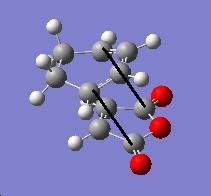 |
2.873 |
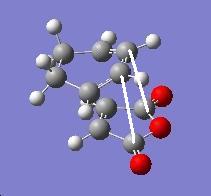 |
2.99 |
Exo transition state:
| Sketch of the C-C bond | Distance (angtroms) |
|---|---|
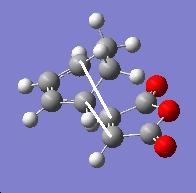 |
2.291 |
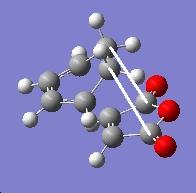 |
3.028 |
The main differences in geometry of the endo and exo structures is the hybridisation of the carbon atoms directly above the O=C-O-C=O fragment of maleic anhydride. For the endo isomer, the carbon atoms are sp2 which makes them planar whereas for exo, they are sp3 hybrididsed and therefore, are not planar. This causes steric clash between the hydrogen atoms of cyclohexadiene and maleic anhydride and pushes the two fragments away. This is also confirmed by the relevant distances (3.028Ã in contrast with 2.99Ã) indicated in the table above. This also causes the C-C σ bond forming distance to be shorter in endo than in exo.
The actvation energy of the endo and exo reactions were also calculated:
| Endo | Exo | |
|---|---|---|
| Combined energy of reactants (Hartrees) | -612.70848 | -612.70848 |
| Energy of transition state (Hartrees) | -612.68340 | -612.67931 |
| Activation energy (Hartrees) | 0.02508 | 0.02917 |
| Activation energy (Kcal/mol) | 15.74 | 18.30 |
As expected, the activation energy of the exo product is higher than the endo product. This also addes to the endo selectivity observed in this particular reaction.
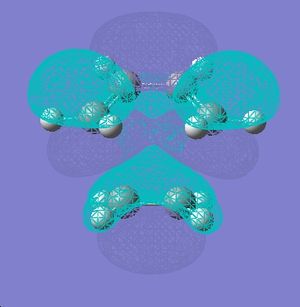
Next, we will look at the frontier orbitals of the reactants and transition states and explain which reactants' HOMO reacts with the other's LUMO orbital. The symmetries of orbitals will be mentioned with respect to the plane of symmetry shown on the HOMO of Cyclohexadiene.
Reactants:
| Maleic anhydride | Cyclohexadiene | |
|---|---|---|
| HOMO |  |
 |
| LUMO |  |
 |
The HOMO orbitals of both reactants are symmetric whereas the LUMO's are antisymmetric. Following is table which displays the frontier orbitals of the Exo and Endo transition states.
Transition states:
| Endo | Exo | |
|---|---|---|
| HOMO |  |
 |
| LUMO | 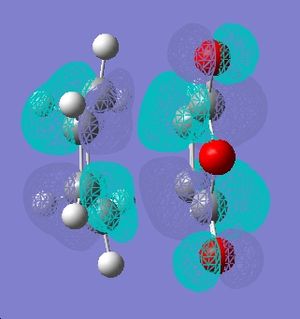 |
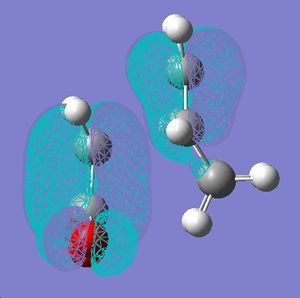 |
None of the orbitals above are symmetric. Therefore, the orbitals that would interact to give these should be antisymmetric. The HOMO of cyclohexadiene and LUMO of maleic anhydride is antisymmetric, hence these orbitals would combine during the course of the reaction. Indeed this was expected, the electron withdrawing C=O substituents of maleic anhydride renders the HOMO orbital eletron deficient and therefore, it's LUMO is involved. The diene is electron rich in this reaction and therefore, it's HOMO orbital is involved in forming the new C-C sigma bond. This is known as the normal eletron demand. Normal electron demand is defined as, when eletron donating groups are on the diene and electron withdarwing groups such as in this case (maleic anhydride)are on the dieneophile. The Diels Alder reactions are expected to be accelerated in this case. The HOMO of diene and the LUMO of dienophile react to give the HOMO of resulting molecule[4]. Opposite is true for an inverse electron demand reaction.
In the next section, we will try to explain this effect observed by substitution of electron withdrawing groups with electron donating groups on the dienophile.
The reaction of butadiene and ethene-1-ol
The previous section illustrated an example of a normal eletron demand Dield Alder reaction. To demonstrate the opposite inverse eletron demand reaction ethene substituted with an eletron donating OH group was optimised and a transition state formed as a result of its reaction with butadiene was observed.
One negative frequency was calulated at -543.798cm-1 which was annotated and is shown below with displacement vectors:
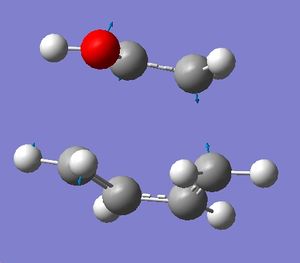
The frontier orbitals were generated for the starting materials and the transition state using the 6-31G(d) method.
| Butadiene | Ethene-1-ol | Transition state | |
|---|---|---|---|
| HOMO | 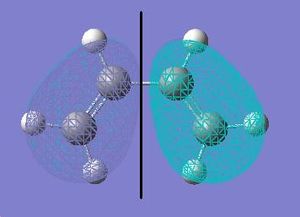 |
 |
 |
| LUMO |  |
 |
 |
As can be seen, only the LUMO orbital of butadiene is symmetric out of all the molecular orbitals displayed, with respect to the plane of symmetry indicated by the black line. The HOMO of the transition state is antisymmetric, therefore we need antisymmetric orbitals of the reactants to react. According to inverse electron demand, the HOMO of the dienophile is electron rich and takes part in bonding. Unfortunately, this is not the case in this example. The antisymmetric HOMO of butadiene would undergo bonding with the LUMO of ethene-1-ol, in a similar way as maleic anhydride and cyclohexadiene. Hence, substituting only one OH group did not have a strong enough electron donating effect on the dienophile. Maybe, we could have repeated calcualtion by putting a stronger electron donating group as well as subsituting an electron withdrawing group on the diene to illustrate the inverse electron demand. Unfortunately, due to time constraints, it was not possible to carry out further calcualtions.
Conclusion
The experiment has illustrated the use of computation methods to locate a transition state which is produced during the course of a reaction but can not be isolated. The energies and molecular orbitals of such species were predicted fairly accurately which in reality could be proved to give a lot of useful information which may not be accessible through experiments in laboratory. The transition states have helped explain selectivities observed in the famous Diels Alder reaction. We could extract more information using better computational methods but due to time constraints, it was not possible during this session.
References
- Physical Module script: http://www.ch.ic.ac.uk/wiki/index.php/Mod:phys3
- http://www.kayelaby.npl.co.uk/chemistry/3_7/3_7_3.html (Accessed 22 February 2009)
- Frontier Orbitals and Organic Chemical Reactions, Ian Fleming., pg 107, 108
- http://dspace.maag.ysu.edu:8080/dspace/bitstream/1989/7825/2/b19606199.pdf (Accessed 26 February 2009)
