Rep:Mod:zaininorganic
Module 2: Bonding (Ab initio and density functional molecular orbital
Objectives of this module:
Computational Chemistry is a vital tool in predicting stability of isomeric structures and the bonding present in them. It can also be used to locate the transition states formed during the course of a chemical reaction which is impossible to observe or characterise experimentally. This module concentrates on determining properties such as IR spectra to differentiate between isomers, electron density and molecular orbitals to obtain information on bonding and interactions between atoms.
Optimising Boron trichloride, BCl3
Boron trichloride was optimised using Gaussian. As it is a small molecule, the calculations were performed on the laptop which only took a few seconds. The results are tabulated as follows:
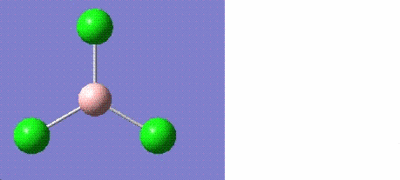
Bond angles = 120.0o Bond lengths = 1.87 angstroms
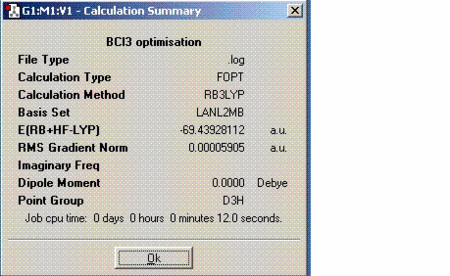
At this time, it is worth looking at the gradient to check whether the calculations have actually run or not. In order to confirm, the gradient must be close to 0, less than 0.001. From the value tabulated above, it can be said that the as successfully optimised.
As 1KJ/mol is approximately equal to 0.00038 hartrees, the energy of BCl3 is approximately equal to -182313 KJ/mol. Another thing to note is that the molecule does not have a dipole moment. Although B-Cl bond is polar, the net dipoles in this molecule cancel out because the molecule is highly symmetric, therefore giving no net dipole moment.
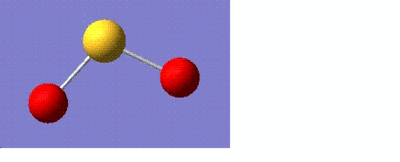
Optimising sulphur dioxide
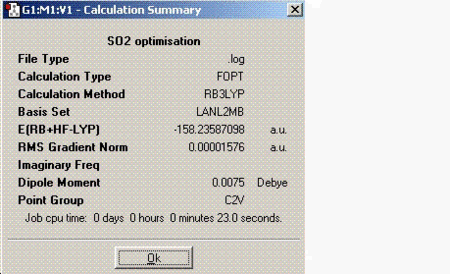
For this part of the module, a small molecule such as sulphur dioxide (SO2) was chosen and information was found about it using the same principles as before. This time the calculations were sent for scan instead of performing on the laptop. The information about SO2 is tabulated below:
Input orientation: --------------------------------------------------------------------- Center Atomic Atomic Coordinates (Angstroms) Number Number Type X Y Z --------------------------------------------------------------------- 1 16 0 0.000000 0.000000 0.000000 2 8 0 0.000000 0.000000 1.670000 3 8 0 1.574211 0.000000 -0.557457
Bond length = 1.74 angstroms Bond angle = 106.4o
SO2 molecule has an overall dipole moment since it is not as symmetric as BH3. The net dipoles do not cancel out thus giving a non-zero dipole moment.
Vibrational analysis and molecula orbitals of boron hydride, BH3:
In this exercise, the vibrations of a simple molecule like BH3 are found. BH3 was optimised first similarly using DFT-B3LYP technique and 3-21G as the basis set. Then the frequency calculation was performed on the optimised structure. The information about this molecule along with the vibrational analysis is as follows:
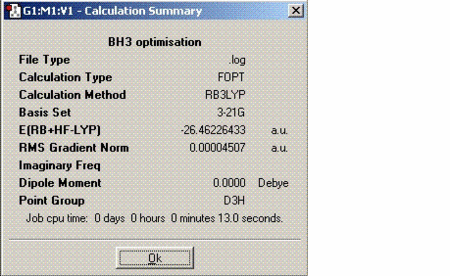
As expected BH3 does not have any dipole moment. The B-H bond length (1.19 angstroms) is significantly shorter compared to B-Cl bond length calculated above (1.87 angstroms) due to the more effective overlap between the boron and hydrogen orbitals which are of similar size and energy.
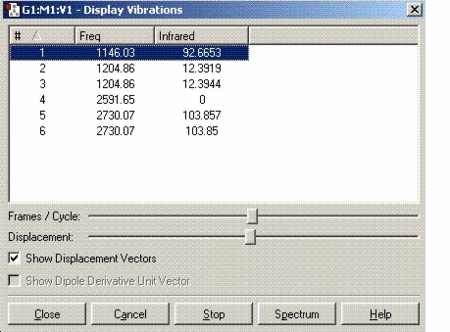
Vibrational analysis
| Vibration number | Vibration form | Symmetry |
|---|---|---|
| 1 |  |
A,,2 |
| 2 |  |
E' |
| 3 | 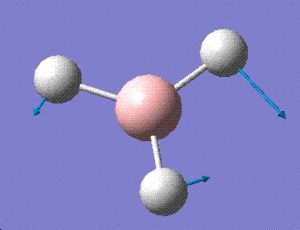 |
E' |
| 4 |  |
A1' |
| 5 | 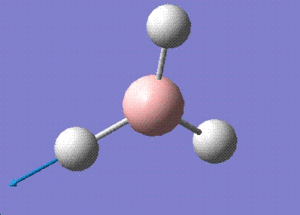 |
E' |
| 6 | 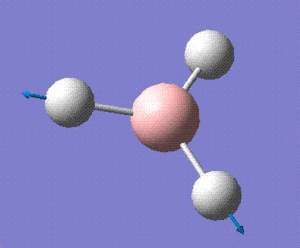 |
E' |
The IR spectrum obtained as a result is as follows:
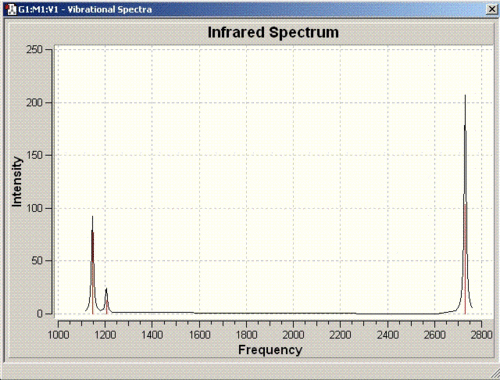
For a non linear molecule such as BH3, the total number of vibrations is given by the formula is 3N-6. Since there are 4 atoms in total, 6 vibrations are observed for this molecule. However, all these vibrations may not be visible on the spectrum due to weak or similar intensities. As for BH3, the vibration at 2592cm-1 has an intensity of zero which does not appear on the spectrum provided above. The vibrations at 1204 and 2730 cm-1 have the same intensities so only one peak for each is observed.
Molecular orbitals of BH3
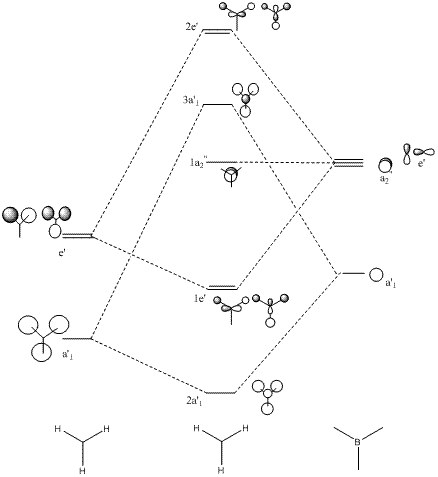
The quantitative molecular orbitals for BH3 were also formed from these techniques which were compared with the qualitative orbitals obtained from simple MO diagrams as illustrated below:
MO diagram of BH3:
| Quantitative molecular orbital | molecular orbital symmetry |
|---|---|
 |
1a' |
 |
2a' |
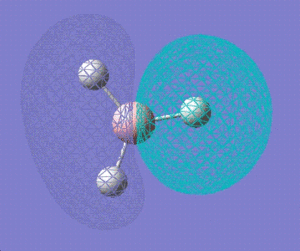 |
1e' |
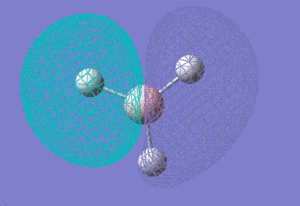 |
1e' |
 |
1a2,, |
The computed molecular orbitals are not very different from those predicted from the molecular orbital theory. The electron densities within the orbitals can be predicted fairly accurately from the qualitative molecular orbitals drawn, thus proving that MO theory is an accurate and reliable technique for predicting molecular orbitals.
The quantum nature of ammonia
Optimisation process of ammonia
In this section, the effect of symmetry on the structure, optimisation time and energies of ammonia was studied. There are three symmetries considered; C3V, C1 and D3h. Due to little energy difference between the two C3V structures of ammonia, the hydrogen atoms on nitrogen undergo an inversion from one side of nitrogen to another through quantum tunnelling and pass through a D3h planar symmetry.
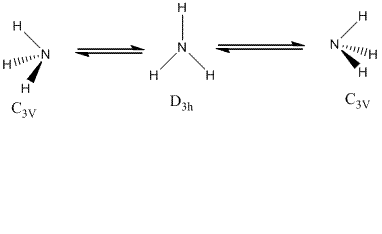
| C3V | C1 | D3h | ||
|---|---|---|---|---|
| Final optimised structure |  |
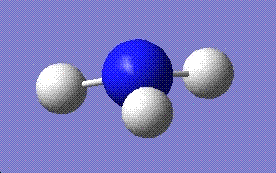 |
 | |
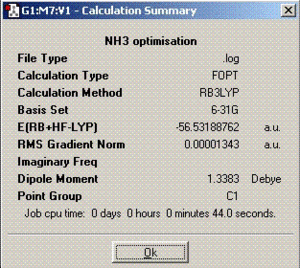
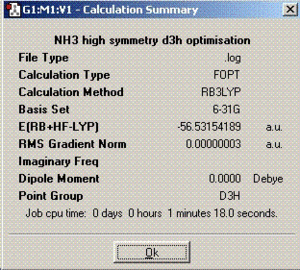
| Summary | 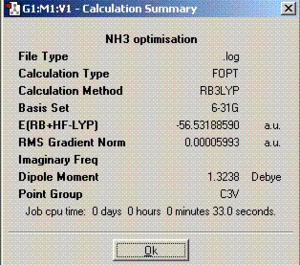 |
 |
 |
The dipole moment for ammonia is greater compared to BCl3 and SO2 due to the larger difference of electronegativities.
| NH3 symmetry | Bond angle | Bond distance (angstroms) | Minimum energy (KJ/mol) | Energy difference | |
|---|---|---|---|---|---|
| C3V | 116.2 | 1.00 | -148424.477737 | - | |
| C1 | 116.1 | 1.00 | -148424.482253 | 0.0045 | |
| D3h | 116.2 | 1.00 | -148424.477737 | 0.9032 |
As can be deduced from the optimisation calculations above, symmetry has an effect on the time needed to finish the calculations and structures of the molecules. The more symmetrical molecules take shorter times to optimise as they do not move around in many ways. Therefore, C1 should have the longest optimisation time. During the optimisation process, the symmetry of the molecule is tried to be kept the same as the original molecule unless the ’ignore symmetry’ box is checked but it is ignored if it is not checked as was done for C1 geometry.
From the calculated energies in the table above, it can be deduced that the lowest energy geometry of ammonia is the C1 geometry. Since, C1 has no symmetry and is only used as a method to find out whether C3V has the lowest energy. If we look at the optimised structures for both C1 and C3V point group, the structures are same and the physical data extracted is pretty close as well (minimum energy). Therefore, C3V is the lowest energy geometry.
It is worth mentioning that the energy calculated using the computation techniques is not very accurate (5-10 KJ/mol). Since the difference calculated in the energies for the D3h and C3V geometries is less than 5KJ/mol, it cannot be said very accurately which geometry has the lowest energy. Therefore, these results are only approximate.
The energy difference between C1 and the higher energy states is also given in the table above.
The energy for the inversion process at room temperature is equal to 2.48KJ/mol whereas the energy difference calculated between C3V and D3h geometries is less than this value (0.90 KJ/mol). This means that at room temperature, this inversion process takes place easily. But, later in the report it will be proved using a more accurate technique, this process is actually disfavoured.
The second part of this section involves optimisation of ammonia molecule using better methods and basis set and its effect on the time needed to complete calculations, the final geometry and energies. The method employed was MP2 with 6-311+G(d,p) basis set.
Better optimisation techniques for ammonia
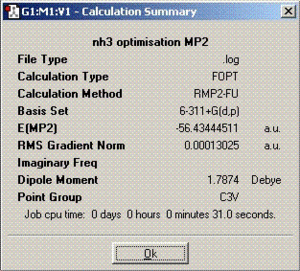
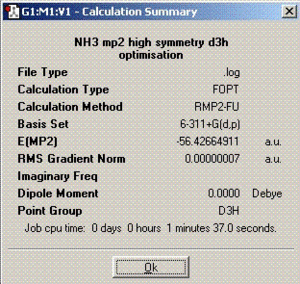
MP2 technique produces more accurate final structure of the molecule and therefore, the optimisation times are longer compared to the ones obtained in the previous section. The barrier height to inversion calculated from MP2 calculations is 20.53 KJ/mol in contrast to 0.90 KJ/mol calculated from B3LYP. Comparing these with the experimentally calculated value of 24.3 KJ/mol, it can be concluded without any doubt that MP2 calculation technique is much more accurate and reliable. According to these results, the inversion process should not take place at room temperature. However, it has been proven experimentally that the process does happen which is probably due to quantum tunnelling. This is a process in which particles violate the principles of classical mechanics by penetrating a potential barrier higher than the kinetic energy of the particle[1].
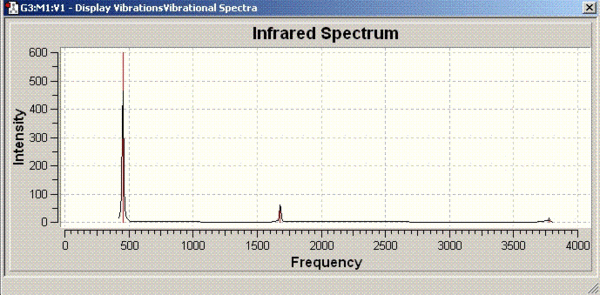
Vibrational analysis of ammonia
| Symmetry | Vibrational bands | IR spectrum |
|---|---|---|
| C3V | 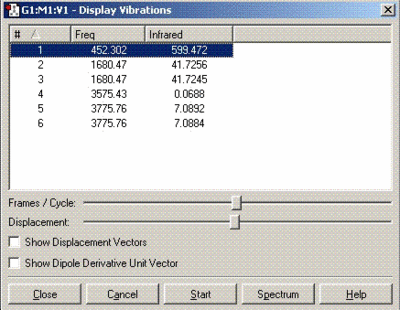 |
 |
| D3h |  |
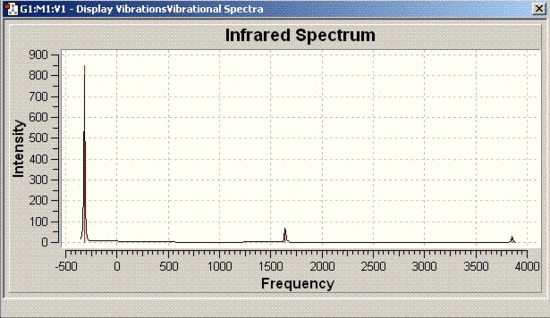 |
The vibrational frequencies for C3V structure have all positive values as shown above but, the D3h molecule has one frequency with a negative value (-318 cm-1). Therefore, it can be concluded that D3h molecule is the transition state of this inversion process.
The first 4 vibrational modes (1, 2, 3 and 4) shown in the table above of both structures have the same character of motion. The vibrational frequencies calculated are compared with those obtained from the literature in the table below:
| Number | Literature frequency[2]/cm-1 (C3V) | Obtained frequency (cm-1) |
|---|---|---|
| 1 | 950 | 452 |
| 2 | 1627 | 1680 |
| 3 | 3337 | 3575 |
| 4 | 3444 | 3775 |
The IR frequencies obtained from our calculations do not match too well with the literature values especially the first frequency which is significantly different. This is probably due to the B3LYP calculations performed is not very accurate. The barrier height to conversion calculated for C3V earlier (0.79 KJ/mol) showed a large difference when compared to 24.3 KJ/mol (literature value) which indicates that the first frequency from the table above (452 cm-1) follows the inversion reaction path.
Isomers of Mo(CO)4L2:
Optimisation results
For this exercise, the ligands L were chosen to be trimethylphosphine groups. There are two possible stereoisomeric forms adopted by this molecule. Cis in which the P(CH3)3 groups are cis to eachother and trans in which they are at an angle of 180o. The number of carbonyl vibrational bands that appear in the spectrum is dependent on the symmetry of the molecule. Cis molecule therefore shows 4 carbonyl bands in contrast to one for trans isomer.
Due to the large size of the molecule, the optimisation process was carried out in three parts to get good results including a vibrational analysis. The optimised structures are as follows:
Cis isomer:
Trans isomer:
The bond lengths and angles calculated from the B3LYP/LanL2MB are tabulated below:
| Cis isomer | Cis isomer lit [3] | trans isomer | trans isomer lit [4] | |
|---|---|---|---|---|
| Mo-P bond length | 2.74 | 2.52 | 2.65 | 2.50 |
| P-Mo-P bond angle | 93.1 | 97.5 | 180 | 180 |
| Mo-C bond length (equatorial CO) | 1.99 | 1.97 | 2.05 | 2.01 |
| Mo-P bond length (axial CO) | 2.05 | 2.03 | - | - |
The literature bond length of Mo-P is higher than the one obtained from the calculations. This is due to the phosphorus d orbitals have not been taken into account. Given that phosphine ligands are good π acceptors, they make used of these low lying d-orbitals to accept electron density from the metal. Therefore the next calculation (B3LYP/lanL2DZ) performed takes these orbitals into consideration during the calculations.
The bond lengths and angles calculated as result are as follows:
| Cis isomer | Cis isomer lit [3] | trans isomer | trans isomer lit [4] | |
|---|---|---|---|---|
| Mo-P bond length | 2.65 | 2.52 | 2.57 | 2.50 |
| P-Mo-P bond angle | 95.3 | 97.5 | 180 | 180 |
| Mo-C bond length (equatorial CO) | 1.98 | 1.97 | 2.03 | 2.01 |
| Mo-P bond length (axial CO) | 2.03 | 2.03 | - | - |
Optimisation results after using a better method show a very good match with the literature results by lowering the MO-P bond length.
Infra Red analysis:
The IR spectra of the two molybdenum isomers contain different number of vibrational bands and this is shown from the computational calculations performed in this section.
| Cis isomer (cm-1) | Cis isomer intensity | Cis isomer lit [5] Mo(CO)4[P(n-Bu)3]2 | trans isomer Mo(CO)4[P(n-Bu)3]2 (cm-1) | trans isomer lit [5] | trans isomer intensity |
|---|---|---|---|---|---|
| 1848 | 1069 | 2012.4 | 1839 | 1866.1 | 1998 |
| 1851 | 1961 | 1913.7 | 1840 | 1885.4 | 2010 |
| 1870 | 666 | 1898.5 | 1883 | 1933.9 | 0 |
| 1960 | 322 | 1866.7 | 1955 | 2050.4 | 0 |
As can be seen from the vibrational frequencies above, cis isomer has four distinct bands with reasonable intensities which makes them all visible in the IR spectrum.
The trans isomer shows 4 vibrational bands as well but the first two stated in the table have similar frequencies and intensities and therefore, possibly show one peak in the IR spectrum. The other two bands have zero intensity and therefore would not appear in the IR spectrum. Thus it has been proven that the trans isomer would only only show one distinct carbonyl peak as observed in the literature spectrum. Thus this technique has proven to be a useful tool in predicting IR spectra of compounds fairly accurately and differentiating between stereoisomers.
However, the literature data does not match the obtained frequencies too well. The literature reports three frequencies for the trans isomer but there were no comments on whether their intensity was high enough that they were visible in the IR spectrum.
Examining the relative energies of two isomers:
| Cis isomer energy (KJ/mol) | trans isomer energy (KJ/mol) | energy difference | ||
|---|---|---|---|---|
| LanL2MB | -2007154 | -2007130 | 1839 | |
| LanL2DZ | -2030457 | -2030450 | 7 |
Although the energy for the trans isomer is higher, the PMe3 ligands prefer to adopt a trans configuration according to the literature so as to minimise the steric hindrance between the bulky the phosphine ligands. Again the energy calculations have proven to be less accurate to what is observed experimentally. This shows that the structures have not been optimised too well. To prove that the trans isomer is more stable we could run calculations using another method which adds the phosphorus d orbitals and therefore give better results.
Although the energy for the trans isomer is higher, the PMe3 ligands prefer to adopt a trans configuration according to the literature so as to minimise the steric hindrance between the bulky the phosphine ligands. Again the energy calculations have proven to be less accurate to what is observed experimentally. This shows that the structures have not been optimised too well. To prove that the trans isomer is more stable we could run calculations using another method which adds the phosphorus d orbitals and therefore give better results.
This preference can be changed by substituting п accepting ligands with п donating ligands. To prove this using computational calculations, we chose piperdine ligands. The optimisation results are tabulated below:
| Cis isomer | trans isomer | |
|---|---|---|
| Energy (KJ/mol) | -2658753 | -2655515 |
| publish link | DOI:10042/to-1970 | DOI:10042/to-1975 |
From the energy values above, the Cis isomer has been proven to be more stable by a considerable amount. The bond angle between the two trans carbonyl ligands was 170.8o instead of 180o. This was due to the bulky piperidine ligands which have forced the carbonyl ligands towards eachother.
Grignard reagents in solution
Introduction
Grignard reagents involving magnesium metal undergo an equilibrium reaction in organic electron donor reagents and can be described by the following reaction.
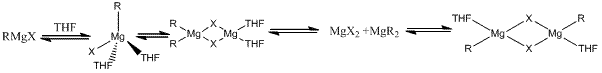
Where X =halide (Chlorine), R = methyl (CH3).
In the presence of ethereal solvents (diehtylether or tetrahydrofuran), the equilibrium lies in the favour of alkyl or aryl magnesium halide product [6]. Generally the amount of each species depends upon [7]:
- The size and electronic nature of R group
- The size and electronic nature of halide group
- The nature of the solvent
- Concentration and temperature
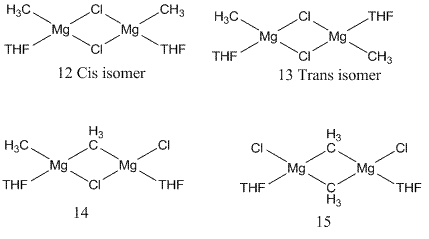
It is observed that halide substituents prefer to take the bridging position instead of the alkyl groups. In my calculations, I have chosen four possible positions that the alkyl and halide groups can take around magnesium and the effect on the bond distances, energy and vibrational spectrum of the resultant isomers.
Optimisation process and results
The structures shown below were optimised in three steps to give optimum results. Firstly a B3LYP-LanL2MB calculation were performed followed by B3LYP-LanL2DZ which takes into account the d orbitals and therefore give better results. Vibrations frequencies were then calculated using the fully optimised structures.
| Isomer | Optimised structures | Energy (KJ/mol)LanL2DZ | Energy (KJ/mol LanL2MB | published link | ||
|---|---|---|---|---|---|---|
| Monomeric specie | - | -1350786 | DOI:10042/to-2012 | |||
| 12 | -1513625 | -1496023 | DOI:10042/to-2016 | |||
| 13 | -1513636 | -1496038 | DOI:10042/to-2015 | |||
| 14 | -1513599 | -1495960 | DOI:10042/to-2017 | |||
| 15 | -1513594 | -1495919 | DOI:10042/to-2018 |
Monomeric CH3MgCl.2THF was optimised using B3LYP/LanL2MB to determine whether the equlibrium mixture favours the formation of the dimer or prefers staying at the monomeric species side. The opmisation results show that the energy of the monomeric grignard reagent in the organic solvent is significantly higher than the dimer, therefore the monomer is more unstable and hence, leads to the formation of the dimer in organic solvents.
The next section will discuss which of the possible dimers above are the most stable and hence formed as a result of the equlibrium reaction.
Comparing the energies of all isomers above, it can be said that halide bridging is preferred over methyl bridging as mentioned in the literature as structure 13 has the lowest energy of all. Analysis of the cis and trans isomer energies of dihalide bridging compounds, cis isomer in which both methyl groups are on the same side has a higher energy and hence it is disfavoured. This could be best explained in terms of the steric clash between the two tetrahydrofuran rings which are on the same side and in the same plane as well. However, it can not be said with absolute certainty that trans is preferred over cis conformation since the energy difference between the two isomers is approximately 10KJ/mol and the techniques we are using are not very accurate. Another difference between 12 and 13 is the position of the THF groups relative to each other. In 12 they are orientated in the same plane whereas in 13, they are perpendicular to eachother to minimise steric clash. Alkyl bridging is not favoured at all since as 15 has the highest energy out of all the structures in which both methyl groups have taken the bridge positions.
| isomer | Bond length Mg-Cl (bridging) | Bond length Mg-C (bridging) | Bond length Mg-O | Bond angle Cl-Mg-Cl (bridging | Bond angle C-Mg-C (bridging) | Bond length Mg-C (non-bridging) | Bond length Mg-Cl (non-bridging) |
|---|---|---|---|---|---|---|---|
| 12 | 2.52 | - | 2.03 | 90.6 | - | 2.10 | - |
| 13 | 2.52 | - | 2.04 | 91.9 | - | 2.10 | - |
| 14 | 2.47 | 2.21 | 2.04 | 75.1 | 85.1 | 2.10 | 2.33 |
| 15 | - | 2.23 | 2.04 | - | 74.1 | - | 2.34 |
Generally, bridging bond distance for Mg-C and Mg-Cl bonds are found to be longer than the normal Mg-C and Mg-Cl bonds. This is due to the fact that bridging bonds are formed as a result of 2e-3c interactions. This means that the electron density in that region is distributed between three atoms instead of being shared equally between two atoms such as in normal covalent 2e-2c bonds, leading to longer and weaker bonds. The energies above prove that the bridging bonds are longer compared to normal 2e-2c bonds as the Mg-Cl and Mg-C bridging bond lengths are longer than the corresponding non-bridging bond.
As the bond length is decreasing between the metal and bridging atoms, the bond angle increases. Cl-Mg-Cl bond angles are closer to 90o compared to C-Mg-C bond angles which is 85.1o in 14 and even smaller (74.2o) in 15. The following table shows some of the literature bond lengths found but not of the same structure. Therefore, the bond distances calculated as a result of our calculations may not match very accurately [10].
| Bond length (Mg-Cl bridging) | Bond length (Mg-C non-bridging) | Bond length Mg-Cl (non-bridging) |
|---|---|---|
| 2.53 | 2.15 | 2.29 |
Even though the literature values are not of the same compound that we have analysed, the calculated values still match very well with the above data. This shows that the structures have been optimised pretty well.
An interesting fact to notice from the optimised structures is that the distance between magnesium atoms decreases as the methyl group takes the bridging position until a Mg-Mg bond forms in the dimethyl bridging complex. The magnesium carbon bond distance is smaller compared to Mg-Cl, therefore as the methyls are bridged, magnesium atoms come close enough that they can form bonds. This value matches well with the Mg-Mg literature distance of 2.85 angstroms [8].
| Isomer | Mg-Mg distance |
|---|---|
| 12 | 3.58 |
| 13 | 3.62 |
| 14 | 3.05 |
| 15 | 2.71 |
Molecular orbitals
Due to time constraints, I chose to calculate the molecular orbitals of only structures. Structures 12 and 14 were chosen to see the effect of replacing one bridging chlorine by a methyl group on the frontier orbitals. In addition, to see the effect of oxidation reaction on 12, the molecular orbitals of 12 but with a +2 charge was also measured. The optimisation process for a charged species is same but only a minor change is made in the input file as shown below. The charge was change to 2 instead of zero to obtained the optimised structure and hence, the molecular orbitals from it.

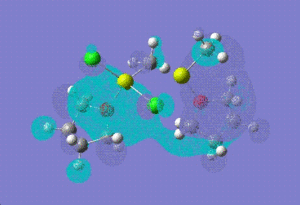
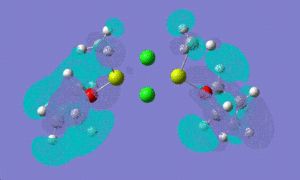
| molecular orbital | 12 | 14 | [12]+2 | |
|---|---|---|---|---|
| HOMO -1 | 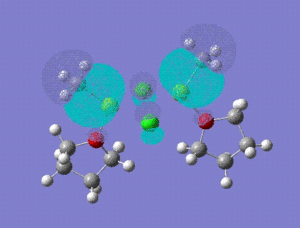 |
 |
 | |
| HOMO | 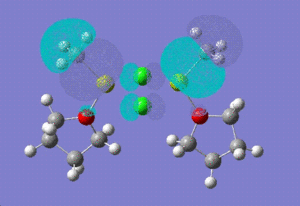 |
 |
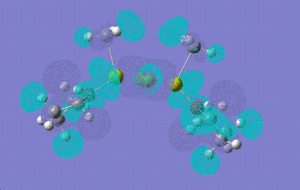 | |
| LUMO | 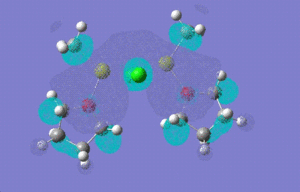 |
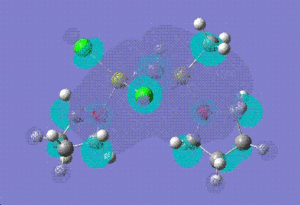 |
 | |
| LUMO +1 |  |
 |
 |
The file for the charged structure is published with the link as follows followed by a discussion on the molecular orbitals obtained:
[12]+2:
HOMO -1: It has most of the electron density concentrated towards the THF rings equally on both sides of the molecule, therefore the antibonding and bonding orbitals lie mostly on the THF rings. There is no electron density at all between Mg-Cl bond bridging bonds. HOMO: Electron density evenly distributed throughout the whole of the molecule. Contains 91 bonding orbitals in contrast TO 58 for the other two.
12:
HOMO -1: Most of the electron density and hence the molecular orbitals lie on the bridging chlorine atoms and Mg-CH3 bonds. Almost none in the THF rings. HOMO: Electron density nicely distributed between the chlorine atoms and Mg-CH3 bonds. This means that when the Grignard dimer molecule undergoes oxidation reaction, the electron come out of the HOMO orbital which means that electron density is removed from Chlorine and Mg-CH3 bonds.
To investigate which part of the molecule loses most of its electron density upon oxidation , we need to look at the HOMO orbital of 12 and the new HOMO orbital of the charged dimer. The potential site from where the electron density can be removed have been discussed above. The HOMO orbital of the charged dimer has a significantly reduced size of the Mg-CH3 molecular orbital and hence electron density around this bond. The orbitals around the bridging chlorine bonds appear to be the same, hence it can be concluded that the electrons are lost from the Mg-CH3 part of the molecule.
Comparing the energies of the charged isomer with all four isomers above, it can be deduced that [12]+2 would be most unstable as it has the highest energy (-1511855) out of all isomers. Therefore, we would not expect grignard reagents to exist as +2 charged species in a solvent like THF.
14:
Homo -1: The molecular orbitals are no more symmetry distributed. They are more inclined towards the non-bridging chlorine atom and there is no electron density around the non briding methyl group. HOMO: The Homo orbital looks pretty much the same as HOMO -1 but the major difference is that the electron density and orbitals that were on Mg-Cl (non-bridging) have now shifted entirely onto the MgCH3 (non-bridging) bond. We would therefore expect to see loss of electron density from this side of the molecule if this structure was to undergo oxidation.
Vibrational analysis
This section posed a problem at first as the frequencies for 13, 14 and 15 had one negative frequency each unexpectedly. After putting in a lot of effort and a long discussion with Dr. Patricia Hunt, I managed to optimise the structure well and get all positive frequencies for all four isomers. However, it was realised that it is important to run the frequency calculations at the same level as the optimisation has been done for the molecule. Therefore, to get all positive frequencies, the structures were optimised first at the B3LYP-LanL2DZ level, setting Calculate Force constants to Once and then the frequency calculations were run making sure that the keywords int=ultrafine scf=conver=9 were added to the input file.
| isomer | stretching frequency/cm-1 (Mg-Cl bridging) | Stretching frequency (cm-1) Mg-Cl (non-bridge) | Stretching frequency (cm-1) Mg-C (bridge) | Stretching frequency (cm-1) Mg-C (non-bridge) |
|---|---|---|---|---|
| 12 | 321 | - | - | 568 |
| 13 | 313 | - | - | 567 |
| 14 | 419 | - | 323 | 555 |
| 15 | - | 397 | 272 | - |
The literature vibrational frequencies were found for monomeric EtMgCl.Et2O [9].
| C-Mg (stretch) | Mg-X (stretch) | |
|---|---|---|
| Frequency (cm-1) | 554.6 | 352 |
The literature vibrational frequencies above are for non-bridging atoms. The Mg-C and Mg-Cl non-bridging frequencies calculated from DFT calculations match well with the literature bands. Another thing to notice is the difference in value of stretching frequencies of Mg-Cl and Mg-C bridging frequencies with the non-bridging ones. As explained earlier, bridging bonds are 2e-3c bonds which make them weaker than the normal 2e-2c bonds. Weaker bonds mean lower value of k (spring strength) which is proportional to the stretching frequency. Hence, leading to smaller stretching frequency of bridging bonds.
The IR spectra obtained are as follows:
| Isomer number | IR spectrum |
|---|---|
| 12 | 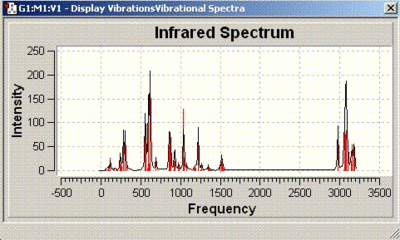 |
| 13 |  |
| 14 |  |
| 15 | 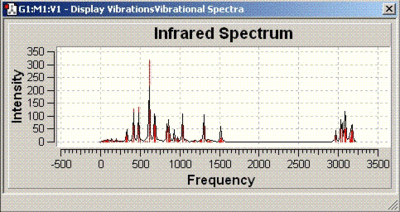 |
Conclusion
Our calculation of the solvated Grignard reagents have led to many interesting obsrevations about the structures and their stability but due the time constraints, other fascinating effects induced upon these structures by substituting chlorine by other halides and replacing methyl groups by other alkyl and aryl substituents could not be found. Comparison with literature data, computational calculations have been proven a very powerfull tool in investing vast amounts of physical data and behaviour of many structures including their isomers and the reactions they undergo.
References
- http://en.wikipedia.org/wiki/Quantum_tunnelling (accessed on Thursday 5th February)
- Yamaguchi, Yukio; Frisch, Michael; Gaw, Jeffrey; Schaefer, Henry F., III; Binkley, J. Stephen, Journal of Chemical Physics (1986), 84(4), 2262-78.
- F. A. Cotton, D. J. Darensbourg, S. Klein and B. W. S. Kolthammer, Inorg. Chem., 1982, 21, 2661-2666
- G. Hogarth. T. Norman ,lnorganica Chimica Acta 254 (1997) 167-171
- D. J. Darensbourg, Inorg. Chem., 1979, 18, 14-17
- http://en.wikipedia.org/wiki/Schlenk_equilibrium (accessed on 15th February)
- 2nd year Lecture notes, Main Group Chemistry, handout 1, pg10.
- Shaun P. Green, et al. Science 318; 1754 (2007)
- Andreas W. Ehlers, Gerard P. M. van Klink, Maurice J. van Eis, Friedrich Bickelhaupt, Paul H. J. Nederkoorn and Koop Lammertsma, J. Mol. Model. 2000, 6, 186 – 194
- Polly L. Arnold, Ian S. Edworthy, Christopher D. Carmichael, Alexander J. Blake and Claire Wilson, Dalton Trans., 2008, 3739–3746
