Rep:Mod:yunzhang Module2

Module 2: Bonding (Ab initio and density functional molecular orbital)

Introduction

Creating a molecule

Step	Image	Procedure
1) Creat a BH3 molecule:		On the controls palette -> click the button that has "a grey periodic table" -> choose "B" for boron -> choose "planar fragment" -> click inside molecule palette: BH3 molecule;
2) BH3 bond length:		On the controls pallette -> click on the button with "a question-mark in front of a ruler(inquiry button) -> click on "B" and "H": bond length= 1.18A;
3) BH3 bond angle:		On the controls pallette -> click on the button with "a question-mark in front of a ruler(inquiry button) -> click on "B" and two adjacent "H"s: bond angle= 120;
4) BH3 change in bond length:	From : to	On the 'molecule window with BH3 -> click the bond distance "button" -> click on one "boron" atom and one "H" atom -> set the "B" atom to be "Fixed"; the "H" atom to be "translate group" and the "bond length" to be "1.5" -> press "OK" -> repeat this procedure for the other two B-H bonds.

Optimising a Molecule of BH3

Method BLYP is used as the type of approximations in solving the Schrodinger equation;
Basis set determines the accuracy. In this case, 3-21G is used, it has a very low accuracy but calculation is quick.
The 1st step for quantum chemical calculation is determine the optimium position of the nuclei for a given configuration otherwise the optimisation might go in the wrong direction and we cannot get the correct optimised structure.

Procedures:  Main menu -> "Calculation" -> "Gaussian":  
             Calculation palette -> "job type" -> change "Energy" to "optimization";
                                    "method" -> change "Hartree-Fock" to "DFT", change "LSDA" to "B3LYP";                         
                                    "title" -> type "BH3 optimisation"
                                    "link 0" -> change "%chk= "yourname_bh3_opt" to "%chk= "yun_bh3_opt" 
                                             -> "submit" -> "%chk=" type "yun_bh3_opt" ->  "submit" -> "save"
                                             -> file name: "yun_bh3_opt" ->  "OK"
             Close the Molecule window

Analysing the optimised BH3 molecule

On "Gaussian 03" -> click "yes" -> In the new window: select file type: "Gaussian Output Files (*.out *.log)

-> select "yun_bh3_opt" file -> click open.

Some geometric information:
 On the comands palette -> click on the button "with a question-mark in front of a ruler"(this inquiry button is used 
 to determine the optimised B-H bond distance and the optimisd H-B-H bond angle)
     
     -> What is the optimised B-H bond distance?
        1.19Å
     -> What is the optimised H-B-H bond angle?
        120.0°

On the results tab -> choose "Summary"; this gives important information about your calculation as shown below:

     -> What is the file type?
        .log
     -> What is the calculation type?
        FOPT
     -> What is the calculation method?
        RB3LYP
     -> What is the basis set?
        3-21G
     -> What is the final energy in atomic units (au)?
        -26.46226438 a.u.(≈ 69477 kJ/mol)
     -> What is the gradient?
        0.00000285 a.u.
     -> What is the dipole moment?
        0.00 Debye
     -> What is the point group of your molecule?
        D3H
     -> How long did your calculation take?
        19.0 seconds

Understanding optimisations: part (a)

On the main menu -> choose "file" -> "open": "File type": "Gaussian Output Files (*.out *.log) -> "File name":selected "YUN_BH3_OPT"
                       -> tick "Read Intermediate Geometries" tick-box checked -> click "open" button: a new molecule window with BH3 after   
                                                                                                       the 1st optimisation.
On the main menu -> choose "results" -> "optimization":

The 1st graph gives the total energy of BH3 molecule vs step of the optimisation which means the program is travelling through the PES of BH3 molecule and finding the minimum energy for the structure. As can be seen from the graph, the energy decreases more rapidly in the earlier optimisation steps than the latter ones and at the end of the optimisation steps, the total energy reaches a plateau, which is the minimum energy obtained under the basis set used.

The 2nd graph gives the gradient of the energy of BH3 molecule vs step of the optimisation, the gradient(first derivative of the PES) is going to reach zero when the geometry approaches the minimum.

At optimisation step 5, the structure has the most negative total energy and corrsponds to the smallest gradient.

The first three structures do not have any bonds but this does not mean there is no bond. It is due to "Bonds" are shown as a structural convenience in Gaussview and the programme draws bonds based on a distance critera which means how close the atoms are and how they interact. Here, the distance of bonds exceed some pre-defined value in the first three optimised structures, therefore the bonds cannot be observed.

Understanding optimisations: part (b)

When optimising geometry, the energy E is calculated based on the frozen position of the nuclei. The stable point (equilibrium position) is obtained by solving the Schrödinger equation for the nuclear positions and electrons, when the nuclear-nuclear repulsion, nuclear-electron attraction, electron-electron interactions are stable as otherwise these interactions will shift nuclei and electrons into a better position. And if this is the case, this change in energy, delta E(R) (first derivative of the E(R) function): we would like the slope to be zero when optimising for the structure of a molecule.

Note: Even though the slope equals to zero, we cannot tell whether the molecule is at a maximum or a minimum point, therefore it is very necessary to carry out the frequency or vibrational analysis to obtain the second derivative. This is because the positive and negative second derivative values indicate a minimum and a maximum for the structure respectively. One negative frequency means we have a transition state and any more than one negative frequencies means the optimisation is incompleted or has failed.

Basis sets and pseudo-potentials

Pseudo-potentials and basis sets is a larger basis set used for higher level of quantum mechanics where the valence electrons are dominated by bonding interactions and the model core electrons are modelled by a special function which named pseudopotential.

Pseudopotential (also called effective core potential) is used as an approximation to replace the atomic all electron potential and thus makes calculations much easier whilst retain the accuracy level approximately.

Basis sets determine the number of functions in describing the electronic structure and is needed to be improved when runing an optimisation for the second row and above atoms.

There are two ways of improving the basis sets:

1)adding more generic functions; 2)add functions that do specific things;

Basis sets in an increasing order: 3-21G, 6-31G(d,p), 6-311+G(d,p).

Using pseudo-potentials

Create a Molecule of BCl3

Procedures: Create a Molecule of BCl3
            file -> new -> create mol group;
            On the controls palette: click on the button with "a grey periodic table" -> choose "Boron"
            -> choose the "planar fragment" -> click once inside the molecule window 
            click the "grey periodic table"table again -> choose "Cl"  -> choose the "atomic fragment" 
            -> click ontop of the "H atoms";
            On the controls pallette: click on the button with "a question-mark in front of a ruler" 
            -> Click "edit" -> click on the "point   group" -> tick-box for "Enable point group symmetry 
            -> choose "D3h" -> set tollerance to "Very tight (0.0001)" and then -> click "OK";
            On the main menu -> choose "Calculation" -> choose "Gaussian";
            On the new palette: "job type" -> change "energy" to "optimization"  -> click on the "method" tab 
            -> change "Hartree-Fock" to to "DFT" -> change "LSDA" to "B3LYP" -> click "title" tab 
            -> type "BCl3 optimisation" -> set "basis set" to "LanL2MB"(N.B.this is a medium level basis set: 
            D95V on first row atoms and Los Alamos ECP (ie pseudo potentials) on heavier elements.) -> "link 0" 
            -> after "%chk=" type "yun_bcl3_opt" -> press "submit" -> file name: "yun_bcl3_opt" -> "save" -> "OK" 
            -> "submit" -> close the molecule window -> "Gaussian Job Completed ...": click "yes";
            On the new window -> file type: "Gaussian Output Files (*.out *.log) -> select "yun_bcl3_opt" 
            -> click "open" -> optimized BCl3 molecule!

Results of BCl3:

On the results tab -> choose "Summary"; this gives important information about your calculation as shown below:

     -> What is the file type?
        .log
     -> What is the calculation type?
        FOPT
     -> What is the calculation method?
        RB3LYP
     -> What is the basis set?
        LANL2MB
     -> What is the final energy in atomic units (au)?
        -69.43928112 a.u.(≈ 182818 kJ/mol)
     -> What is the gradient?
        0.00005905 a.u.
     -> What is the dipole moment?
        0.00 Debye
     -> What is the point group of your molecule?
        D3H
     -> How long did your calculation take?
        15.0 seconds

Accuaracy

the energy will have an error of ≈ 1 kJ/mol, so how much is this in atomic units (which are hartree)?

-> 1 Hartree= 2 625.5 kJ/mol;

the dipole moment will be accurate to about 2 decimal places, ie 0.01 Deby;

frequencies in wavenumbers are by convention reported with no decimal places and for the purposes of this course you need to know that the accuracy is only to around 10cm-1;

intensities are rounded to the nearest whole integer and in fact the accuracy is much less that this;

bond distances are accurate to ≈ 0.01 Å

bond angles are accurate to ≈ 0.1°

Day 1

Independent work

Example: H20

Information obtained are listed as below:

Basis set used	xyz coordination	Comment
Without any optimisation	/	/
3-21G		* bond distances:0.99A * bond angles: 104.0 * calculation method RB3LYP * basis set 3-21G * final energy in atomic units (au) -75.97 a.u. * dipole moment 2.24 * the point group of your molecule C2V * how long did your calculation took 16.0s
6-31G		* bond distances:0.98A * bond angles: 108.3 * calculation method RB3LYP * basis set 6-31G * final energy in atomic units (au) -76.39 a.u. * dipole moment 2.40 * the point group of your molecule C2V * how long did your calculation took 16.0s
6-311G		* bond distances:0.97A * bond angles: 109.2 * calculation method RB3LYP * basis set 6-311G * final energy in atomic units (au) -76.42 a.u. * dipole moment 2.43 * the point group of your molecule C2V * how long did your calculation took 14.0s

The basis sets are used with an increase in a rough order: 3-21G, 6-31G(d,p), 6-311+G(d,p). The first calculations was started with 3-21G basis set, once the structure is optimised, 6-31G was used, finally the structure is optimised under 6-311+G basis set. As larger basis sets are used, the gradient decreases from 0.00011753 to 0.00001696 a.u. (all <0.001) which means as the number of functions used to descripe the electronic structure increases, the structure can be defined more accurately.

Vibrational analysis and confirming minima

The first derivative of a function tells us the slope of the curve whereas the second derivative tells us the curvature of the function, positive value indicates a minimum and negative indicates a maximum.

In here, the frequency analysis is carried out, this is important in determining whether the structure is fully optimised or not.

All positive frequencies means the structure of the molecule is a minimum;
One of frequencies is negative tells us we have a transition state;
Any more are negative the optimisation had failed or incompleted.

The frequency analysis also plays an important role in providing the IR and Raman modes to compare with experiment values.

Procedures:   
  Carry out a frequency or vibrational analysis to confirm we have minium structures:
  On the main menu -> click on file -> "Open" -> fiel type:(*.out *.log)-> YUN_BH3_OPT
 (make sure the structure must be fully optimised)  -> untick the "Read Intermediate Geometries" box 
  -> click "open" -> On the main menu -> choose "file" -> "save" as "yun_bh3_freq.gjf".
  On the main menu -> choose "Calculate" -> choose "Gaussian": On the calculation palette 
  -> "job type": change "energy" or "optmisation" to choose "frequency" -> "Title": type "BH3 frequency" 
  -> under "Additional key words": type "pop=(full,nbo)" -> "submit"

Rusults:

All Results	Atom list	Results summary

Animating the vibrations

Procedures:
  main menu -> choose "Results" -> choose "Vibrations": "Display Vibrations" window -> check no negative frequencies, 
  in this case, no negative frequency(structure has been optimised fully) -> molecule window: rotate BH3 molecule to 
  make it not completely in the plane of the screen -> vibration window: highlight the top vibration -> check 
  "Show Displacement Vectors" box -> click "Start": BH3 starts to vibrate -> height the other 5 vibrations and observe the vibration.

Results and Analysis:

No.	Frequency	Intensity	Symmetry D3h point group	Comment
1	1146	93	A	Three Hs move backwards and forwards through the direction of arrows
2	1205	12	E'	Two Hs come towards and away from each other symmetrically
3	1205	12	E'	All Hs move backwards and forwards in the drection of arrows whereas B is fixed
4	2593	0	A'	All Hs move away from the central fixed B
5	2731	104	E'	Asymmetric stretch between two Hs and the other H remains fixed
6	2731	104	E'	Two Hs move towards and away from the central fixed B following the direction of arrows

The IR spectrum displays 3 peaks whereas the frequency calculation predicts 6 vibrational modes. This difference is caused by the very similar in energy of the vibrational modes 2 and 3; 5 and 6; and since 4 has zero intensity, there are only 3 peaks observed in the IR spectrum.

Molecular Orbitals of BH3

Day 2

Isomers of Mo(CO)4L2

Trans and cis isomers of Mo(CO)4L2 where L=PCH3 were optimised by using the B3LYP method with pseudo-potential LANL2MB
to get the 1st optimised geometry(N.B. type "opt=loose" in the "Additional keywords" box); the 1st optimised geometry was 
optimised further using the B3LYP method with the a better basis set and pseudo-potential optionLANL2DZ,the "opt=loose"
is changed to "int=ultrafine scf=conver=9" to increase the electronic convergence.

Jmol of cis Mo(CO)4(P(CH3)3)2 isomer

Jmol of trans Mo(CO)4(P(CH3)3)2 isomer

Cyclopentasiloxane

Results:

/	LANL2MB: 1st optimisation of cis Mo(CO)4(P(CH3)3)2	D-space	LANL2DZ: 2nd optimisation of trans Mo(CO)4(P(CH3)3)2	D-space
Cis		https://scanweb.cc.imperial.ac.uk/uportal2/?action=publish&subaction=publish&jid=13563		https://scanweb.cc.imperial.ac.uk/uportal2/?action=publish&subaction=publish&jid=13581
Trans		https://scanweb.cc.imperial.ac.uk/uportal2/?action=publish&subaction=publish&jid=13566		https://scanweb.cc.imperial.ac.uk/uportal2/?action=publish&subaction=publish&jid=13583

Compare the computed cis and trans geometries:

/	Total energy after the 1st optimisation/ a.u.	Total energy after the 2st optimisation/ a.u.	Point group	Diple Moment for the 1st optimisation/ Debye	Diple Moment for the 2nd optimisation/ Debye
Cis	-764.48	-773.36	C1	7.27	8.88
Trans	-764.48	-773.36	C1	0	0

Both the cis and trans Mo(CO)4(P(CH3)3)2 adopt a C1 symmetry. The 1st optimisation is higher in energy than the 2nd optimisation for both isomers this is because as a larger basis sets is used, the structures are optimised better and therefore has a lower energy configuration. The dipole moment for the cis isomer increases after the 2nd optimisation, this might due to the dipole has an overall stabilising effect on the molecular structure of the cis isomer, however, for the trans isomer, there is no net dipole moment.The two isomers are comparable in energy so we cannot tell which one is going to form predominately.

Compute the IR frequencies:

Vibrations cis	http://hdl.handle.net/10042/to-1940	Vibrations trans	http://hdl.handle.net/10042/to-1920
C=O stretch(asymmetric) Freqency: 1743 Intensity: 1903	C=O stretch(asymmetric) Freqency: 1748 Intensity: 1009	C=O stretch(symmetric) Frequency: 1782 Intensity: 0	C=O stretch(symmetric) Frequency: 1854 Intensity: 0
C=O stretch(asymmetric) Freqency: 1766 Intensity: 540	C=O stretch(symmetric) Freqency: 1858 Intensity: 420	C=O stretch(asymmetric) Frequency: 1738 Intensity: 1941	C=O stretch(asymmetric) Frequency: 1739 Intensity: 1945

IR spectrum for the cis isomer	IR spectrum for the cis isomer

Compare the computed IR spectra for the cis and trans conformers:

Both IR spectra for cis and trans isomers have one major peak around 1700-1800 which is given rise by the C=O symmetric and asymmetric stretches. It is also interest to note the symmetric stretches for the trans isomer have zero intensity.

Day 3

Ammonia: Introduction and Activities

Inversion processes of ammonia:

When hydrogen atoms are quantum tunnelling a low potential barrier from one C3V symmetry structure of ammonia to its inverted structure, the "inversion doubling" of the vibrational modes of NH3 molecule is induced. The NH3 molecule flips between two states many times per second and the a linear combination of the two states give rise to a "stationary state".

Ammonia: Symmetry

Different isomers of NH3 and the effect of their symmetry on the structures, energies and optimisation time are investigated.

Basis set used: a 6-31G basis set;
Method used: B3LYP.

Jmol

Symmetry

Results Summary

Cyclopentasiloxane

C3V

Bond length of one N-H: 1.01 A
Basis set used: a 6-31G basis set;
Method used: B3LYP;
Tick "ignore symmetry" box in "General";

Jmol

Symmetry

Results Summary

Cyclopentasiloxane

C1

Save file "nh3_b3lyp_d3h.txt" as "nh3_b3lyp_d3h.com";

Open it in Gaussview: an extra pink "atom"(dummy atom)-> run the optimisation.

Jmol

Symmetry

Results Summary

Cyclopentasiloxane

D3h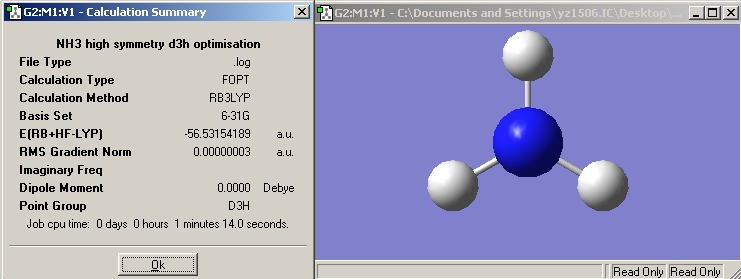

Conclusion:

The symmetry has an effect on the geometry obtained and the more symmetrical the symmetry is, the more time it took to optimise the geometry. A molecule can "break symmetry" during an optimisation only when its symmetry is not constrained. NH3 with C1 symmetery adopts the lowest energy geometry therefore mostly favoured, however, the energies for thses three molecules with differenct symmetries are very similar, therefore in the case of NH3, the symmetry has a minor effect on the total energy obtained. Energy in kJ/mol:

C3V: -148424.4664  difference in energy: 4.5*10^(-3)
C1: -148424.4709   difference in energy: 0
D3h: -148423.5632  difference in energy: 0.9077

The energy differences between these structures are not significant as NH3 molecules undergo quantum tunelling.

Ammonia: Ammonia Method

Further optimisation by using a better method and baisis set:

basis set: 6-311+G(d,p);
method: MP2.

Procedures:

On the Control menua -> scratch a NH3 molecule -> calculate -> Gaussian:

On the Method tab -> "MP2" -> "basis set": choose 6-311G, in the next pull-down options choose the first option for each -> tick the "include all electrons" box -> submit.

Use the file nh3_mp2_d3h.txt and run this optimization.

	Results Summary
C3V symmetry NH3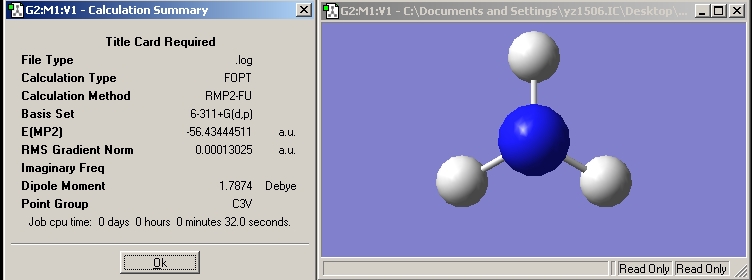

	Results Summary
High symmetry D3H NH3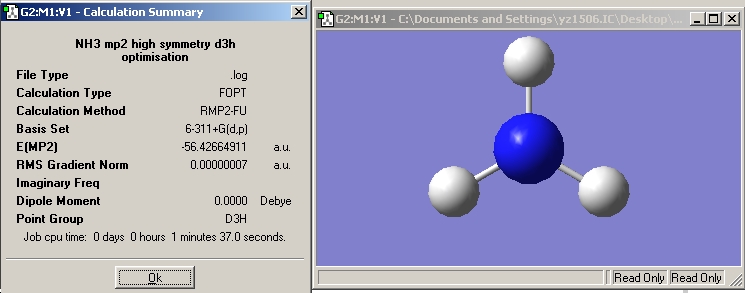

Now, we have optimised the ground state for NH3 under C3V symmetry and the planar inversion transition state which has D3h symmetry.

Conclusion:

how long do these calculations take compared to your lower level ones?

NH3 with C3V symmetry: RB3LYP -> 27sec, MP2 -> 32sec;
NH3 with D3h symmetry: RB3LYP -> 1min 14sec, MP2 -> 1min 32sec;

This calculation time takes longer as MP2 is considered to be a better method and baisis set; since NH3 is only a small molecule the time taken is not a lot, however a much larger molecule the calculations can be very expensive!!

determine the barrier height to inversion by finding the relative energy at this level of calculation ΔE=E(D3h)-E(C3v) in kJ/mol

Difference in energy =(-56.42664911+56.43444511)*2625.5= 20.47 kJ/mol

has ΔE changed much between the B3LYP/6-31G and MP2/6-311+G(d,p) sets of calculations?

Yes, the difference in energy between the higher and lower symmetric structures are increased significantly as MP2 approximates the 
structure more accurately.

how do your results compare to the experimentally determined barrier which is 24.3 kJ/mol?

My result is very close to the experimentally determined barrier and the percentage difference= (24.3-20.5)*100%/24.3=15.6%, in 
order to minimise this %diff even further, a better basis set can be used but on the same hand, it will cost more time.

Ammonia Ammonia: The Inversion Mechanism

Procedures: Save the "nh3_scan_log.txt" as .log file -> open the file in Gaussview(tick "read intermediate geometries") -> choose "View File"

1-D scan of total E and RMS gradient vs scan step number

Structure of NH3 molecule vs scan step number

Ammonia Ammonia: Vibrational Analysis

calculate the frequency analysis for the optimised B3LYP/6-31G C3v and D3h structures and visualise the vibrational spectrum for NH3

Compute the IR frequencies:

Vibrational mode of NH3	(C3v symmetry)	Vibrational mode of NH3	(D3h symmetry)
A1 Freqency: 452 Intensity: 599	E Freqency: 1680 Intensity: 42	A2’’ Frequency: 89 Intensity: 838	E’ Frequency: 1058 Intensity: 53
E Freqency: 1680 Intensity: 42	A1 Freqency: 1680 Intensity: 0	E’ Frequency: 1658 Intensity: 53	A1’ Frequency: 3524 Intensity: 0
E Freqency: 3776 Intensity: 7	E Freqency: 3776 Intensity: 7	E' Frequency: 3737 Intensity: 18	E' Frequency: 3737 Intensity: 18

IR spectrum for the C3v symmetry NH3	IR spectrum for the D3h symmetry NH3

how many positive frequencies are there for the C3v and the D3h structures?

  6 for both.

draw the vibrational modes for both structures (visualise them with gaussview) and match them up, ie which vibrational modes have the same character of motion for the C3v and D3h structures

 Vibrational modes 452 and 89cm-1 don't have the same character since they have different irriducible representations.

which vibration in the C3v and D3h structures "follows" the inversion reaction path?

Both the first vibrational mode in C3v and D3h structures "follows" the inversion reaction path as the Hs moves forwards and backwards along the direction of arrow but the B remains fixed.