Rep:Mod:yrtaxol

EXPERIMENT 1C

Name: Yong R. Tan
CID: 00703262

Part 1

Hydrogenation of Tricyclo[5.2.1.0^2,6]deca-3,8-diene (or commonly know as dicyclopentadiene).

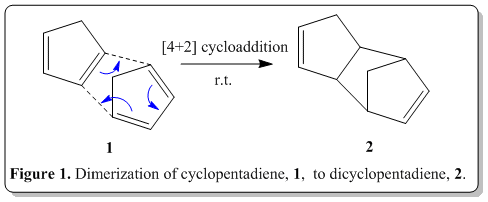
Tricyclo[5.2.1.0^2,6]deca-3,8-diene is readily available inexpensively in coal and tar. Upon reaching, its boiling point (170^o) it would depolymerize back to its monomer, cyclopentadiene, which has boiling point of 41°, and can be distilled off to obtain the pure cyclopentadiene. This process is commonly known as cracking. When left at room temperature, cyclopentadiene eventually dimerizes back to dicyclopentadiene. The polymerization can be determined when there is a change in specific gravity of the compound after some days(specific gravity of cyclopentadiene: 0.805; of dicyclopentadiene, 0.976).

The polymerization process, is actually a Nobel prize winning reaction, namely Diels-Alder reaction. Via the classical Diels-Alder reaction, two cyclopentadiene molecules, 1 would dimerize (as shown in Figure 1) to yield dicyclopentadiene, 2, which is a facile and spontaneous [4+2] cycloaddition reaction at room temperature. The product can either be an exo, 3 or endo, 4 product, as shown in Figure 2.

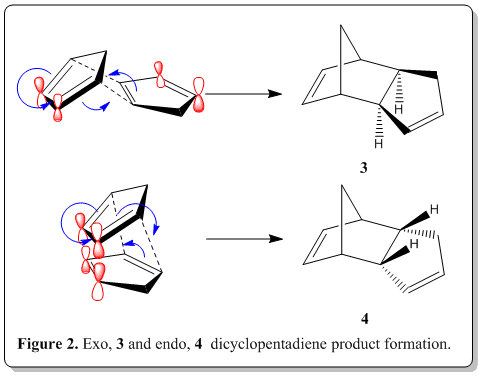
From experimental results reported in the literature, the thermal dimerization gives exclusively the endo dicyclopentadiene, 4 only and does not have any exo dicyclopentadiene, 3 formed. It was known that the endo product is the kinetic product while the exo product is the thromodynamic product. Also, from the studies of Alder and Stein, they indicated that the endo-form had the higher energy content.

Computational analysis of the Tricyclo[5.2.1.0^2,6]deca-3,8-diene was executed with the Avogadro program. The endo and exo dicyclopentadiene geometries were optimized by means of the MMFF94(s) force field option. The alogrithm used was the conjugate gradient option as this evaluates the value of the diagonal terms only while setting all the others to zero. Though it is slower than the steepest descent option, but it assuages the vacillation when reaches less 'steep' gradient where in the steepest descent option, it is very fast but suffer from the vacillation upon reaching less 'steep' gradient. The present results are consistent with the experimental observations and experimental results reported in the literature as mentioned earlier.

Data of dicyclopentadiene MMFF94(s) calculation.

Types of Total Energy	Exo, 3 / kcal mol-1	Endo, 4 / kcal mol-1
TOTAL BOND STRETCHING ENERGY	3.54302	3.46760
TOTAL ANGLE BENDING ENERGY	30.77273	33.19065
TOTAL STRETCH BENDING ENERGY	-2.04139	-2.08217
TOTAL TORSIONAL ENERGY	-2.73105	-2.94978
TOTAL OUT-OF-PLANE BENDING ENERGY	0.01486	0.02198
TOTAL VAN DER WAALS ENERGY	12.80155	12.35764
TOTAL ELECTROSTATIC ENERGY	13.01372	14.18480
TOTAL ENERGY	55.37344	58.19070
Model	Endodimer	Endodimer

From our calculations shown in the table above, the total energy of 3 (exo product, 55.37344 kcal mol^-1) is smaller than of the 4 (endo product, 58.19070 kcal mol^-1). This concur with the results reported by Alder and Stein where the endo product is higher energetic than of the exo product. From the calculation, the endo product is identified as the kinetic product (being higher in energy) while the exo product is identified as the thermodynamically stable product (bearing lower energy).

From the experimental results, the endo dicyclopentadiene, 4 is the sole product but from our calculation, 4 is the conformation with higher energy than of 3(in thermodynamic sense). Yet this is plausible because despite it being the higher energy content, we should inspect the mechanism of the Diels-Alder reaction which lead to the product where stereoselectivity is controlled by stereoelectronic factors. As shown in Figure 2, when the reaction proceeds to form 4, we are able to see that there are bonding interactions between the frontier orbitals (labelled red). The symmetry of the orbitals labelled in red are the same and thus able to have such bonding interactions where in 3, it does not have such advantage. This interaction resulted in this preferred orientation during the transition state. As soon as the cycloaddition is complete, the product had the same orientation as during the transition state as the stereochemistry was already defined, leaving the product being exclusively endo only. The endo product is energetically higher which is a kinetic product and thus we could conclude that the Diels-Alder reaction of dimerization ofcyclopentadiene is under kinetic control, leaving the exo product which is thermodynamically more stable being unformed at all.

Other than that, the two main calculated energies for 3 and 4 that dominated the difference in energy, was the Total Angle Bending Energy (E_AB)and Total Electrostatic Energy(E_E). Both the energies are higher in 4 than of 3. The E_AB for 4 is 3 kcal/mol higher than of 3. This could be attributed to the fact that 4 is the endo product, and the ring would be forced to 'bend' inwards, stressing the bicyclo rings to be bending in a more strained conformation, consequent to the higher E_AB. Also, the E_E of 4 is 1 kcal/mol higher than of 3. As explained earlier, the resultant of the straining of the increases the Coulombic potential within the molecule which resulted in the computed values for E_E.

In short, as this reaction is under kinetic control, despite 4 being the highly energetic configuration, it is formed predominantly.

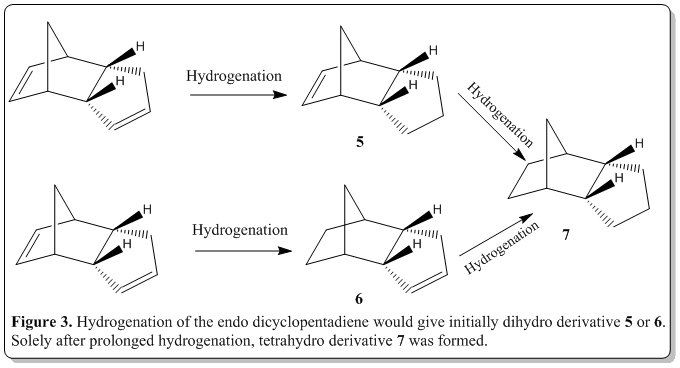
Also, from the endo dicyclopentadiene, when hydrogenation was performed, the dimer would yield, initially one of the dihydro derivative 5 or 6. Then with prolonged hydrogenation, only will the tetrahydro derivative 7 be formed. The reaction scheme is as shown in Figure 3. From the literature, the results was that 6 would be formed predominantly then formation of 7. Would the calculations following the discussion show something that could rationalize this observation?

Computational analysis of 5 and 6 were executed with the Avogadro program. They were optimized by means of the MMFF94(s) force field option. The alogrithm used was the conjugate gradient option as this evaluates the value of the diagonal terms only while setting all the others to zero. Though it is slower than the steepest descent option, but it assuages the vacillation when reaches less 'steep' gradient where in the steepest descent option, it is very fast but suffer from the vacillation upon reaching less 'steep' gradient. The results and conformation of the computed values are summarized below:

Data of dihydro derivative MMFF94(s) calculation.

Types of Total Energy	Endo, 4 / kcal mol-1	Dihydro, 5 / kcal mol-1	Dihydro, 6 / kcal mol-1	Tetrahydro, 7 / kcal mol-1
TOTAL BOND STRETCHING ENERGY	3.46760	5.28510	2.82306	2.68756
TOTAL ANGLE BENDING ENERGY	33.19065	36.54346	24.68552	22.64378
TOTAL STRETCH BENDING ENERGY	-2.08217	-1.83542	-1.65716	-1.51556
TOTAL TORSIONAL ENERGY	-2.94978	-3.70581	-0.37813	3.30168
TOTAL OUT-OF-PLANE BENDING ENERGY	0.02198	0.04191	0.00028	0.00000
TOTAL VAN DER WAALS ENERGY	12.35764	16.41094	10.63690	10.89720
TOTAL ELECTROSTATIC ENERGY	14.18480	5.14499	5.14702	0.00000
TOTAL ENERGY	58.19070	57.88517	41.25749	38.01467
Model	Endodimer	Endodimer	Endodimer	Endodimer

From the calculation being done, it was computed that the hydrogenation product 5 is higher in steric energy than 6 by 16.6 kcal/mol. As from the literature , the ease of forming hydrogenation product 6 is higher than of 5. Combine with the literature value and our calculation, we could postulate that the hydrogenation is under thermodynamic control where the product stability factor predominates in this reaction.

The energies that resulted in the difference in energy were the total bond stretching energy (E_BS), total angle bending energy (E_AB), total torsional energy(E_T), and total Van der Waals energy(E_VDW).The total electrostatic energy of both 5 and 6 are almost similar. In general, E_BS, E_AB, E_T, and E_VDW are all higher in 5 than of 6. The energies listed are higher in 5 than of 6 was due to product 5 still bears the alkene in a five-membered ring but the ring was strained due to it being part of the bicyclic system. On the other hand, the product 6 has the alkene in a five-membered ring but the ring was not part of the strained bicyclic ring and thus it has lower overall strain energy. As the hhydrogenation is under thermodynamic control, 6 is formed first then only with prolonged hydrogenation, 7 is formed. As anticipated, product 7 is lower in energy than 5 and 6. as the whole system does not have any alkene functional groups that strains the whole system and engendered the lowering in energy.

Atropisomerism of a large ring ketone intermediate in one synthesis of the anti-cancer drug Taxol and insights on bridgehead alkene reactivities.

(i) Atropisomerism

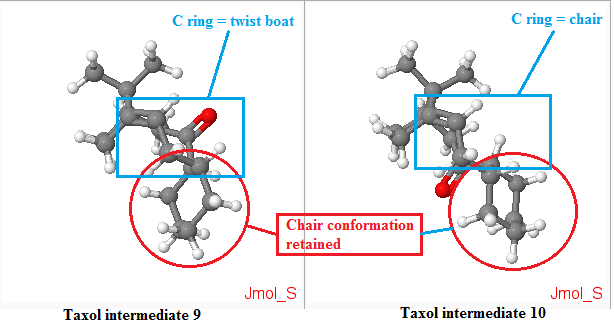
From the literature, compound 8 undergoes oxy-Cope rearrangement to either compound 9 or compound 10. The difference between compound 9 and 10 are the positions of the carbonyl (Colored red in Figure 4.), either pointing up (C ring = twist boat) or down (C-ring = chair). As reported by Elmore, having the carbonyl group pointing up in compound 9 would lock the fused cyclohexane (ring C) into an energitically expensive twist-boat conformation. When the carbonyl group is pointing down, the situation is alleviated where chair-like C ring of 10, non-bonded transannular interactions are heightened within the B ring core of such structure.

Computational analysis of 9 and 10 were executed with the Avogadro program. They were optimized by means of the MMFF94(s) force field option. The alogrithm used was the conjugate gradient option as this evaluates the value of the diagonal terms only while setting all the others to zero. Though it is slower than the steepest descent option, but it assuages the vacillation when reaches less 'steep' gradient where in the steepest descent option, it is very fast but suffer from the vacillation upon reaching less 'steep' gradient. The results and conformation of the computed values are summarized below:

Data of Taxol intermediate MMFF94(s) calculation.

Types of Total Energy	Taxol intermediate, 9 / kcal mol-1	Taxol intermediate, 10 / kcal mol-1
TOTAL BOND STRETCHING ENERGY	7.71700	7.60144
TOTAL ANGLE BENDING ENERGY	28.30969	18.79205
TOTAL STRETCH BENDING ENERGY	-0.06819	-0.14341
TOTAL TORSIONAL ENERGY	0.08236	0.21194
TOTAL OUT-OF-PLANE BENDING ENERGY	0.96319	0.84732
TOTAL VAN DER WAALS ENERGY	33.24990	33.29756
TOTAL ELECTROSTATIC ENERGY	0.29397	-0.05295
TOTAL ENERGY	70.54792	60.55395
Model	Endodimer	Endodimer

From the table above, the Taxol intermediate 9 is higher in energy than Taxol intermediate 10, and the difference is by about 10 kcal mol^-1 higher. The total angle bending energy appeared to be the energy that distinguished the energy difference of 9 and 10. As the cyclohexane ring had the chair conformation retained (as shown in figure below), the main difference is in the strain of the ring as labelled in the blue box in figure below. In the Taxol intermediate 10, the ring is in chair conformation while in 9, it is in twist boat conformation which is the source of the hike in energy for conformation 9. The carbonyl group pointing up or down locks the ring in certain conformation and for this case, when it is pointing down (Taxol intermediate 10), it locks the whole system in much lower energy conformation.

(ii)Stability of bridgehead alkenes

Other than that, it was worth noting that for both the intermediates, there was a bridgehead alkene present. Historically, Bredt Computational analysis of 9, product of hydrogenation of 9, 10 and product of hydrogenation of 10 were executed with the Avogadro program. They were optimized by means of the MMFF94(s) force field option. The alogrithm used was the conjugate gradient option as this evaluates the value of the diagonal terms only while setting all the others to zero. Though it is slower than the steepest descent option, but it assuages the vacillation when reaches less 'steep' gradient where in the steepest descent option, it is very fast but suffer from the vacillation upon reaching less 'steep' gradient. The results and conformation of the computed values are summarized below:

Data of Taxol intermediate MMFF94(s) calculation.

Types of Total Energy	Taxol intermediate, 9 / kcal mol-1	Hydrogenation of 9 / kcal	Taxol intermediate, 10 / kcal mol-1	Hydrogenation of 10 / kcal
TOTAL BOND STRETCHING ENERGY	7.71700	12.29091	7.60144	7.30881
TOTAL ANGLE BENDING ENERGY	28.30969	48.45715	18.79205	25.92577
TOTAL STRETCH BENDING ENERGY	-0.06819	1.21082	-0.14341	0.20145
TOTAL TORSIONAL ENERGY	0.08236	5.68683	0.21194	6.79650
TOTAL OUT-OF-PLANE BENDING ENERGY	0.96319	0.10975	0.84732	0.09989
TOTAL VAN DER WAALS ENERGY	33.24990	41.97101	33.29756	33.41936
TOTAL ELECTROSTATIC ENERGY	0.29397	0.00000	-0.05295	0.00000
TOTAL ENERGY	70.54792	109.72648	60.55395	73.75179
Model	Endodimer	Endodimer	Endodimer	Endodimer

From table above, it was computed that both the product of hydrogenation of the 9 and 10 yielded in product of much higher in energy where for the hydrogenation of 9, the product became about 30 kcal/mol higher in energy! Meanwhile, hydrogenation of 10 becomes 13 kcal/mol higher in energy. Upon detailed inspection on the data for hydrogenatio of 10, it was found that the total angle bending energy (E_AB) and total torsional energy (E_T) were the two contributing energies that raises the overall strain energy of the hydrogenated product of 10. On the other hand, for hydrogenation of 9, the total bond stretching energy (E_BS), total angle bending energy (E_AB), total torsional energy (E_T), and total Van der Waals energy (E_VDW) were the responsible in the massive increase in the strain energy of the hydrogenated product of 9.

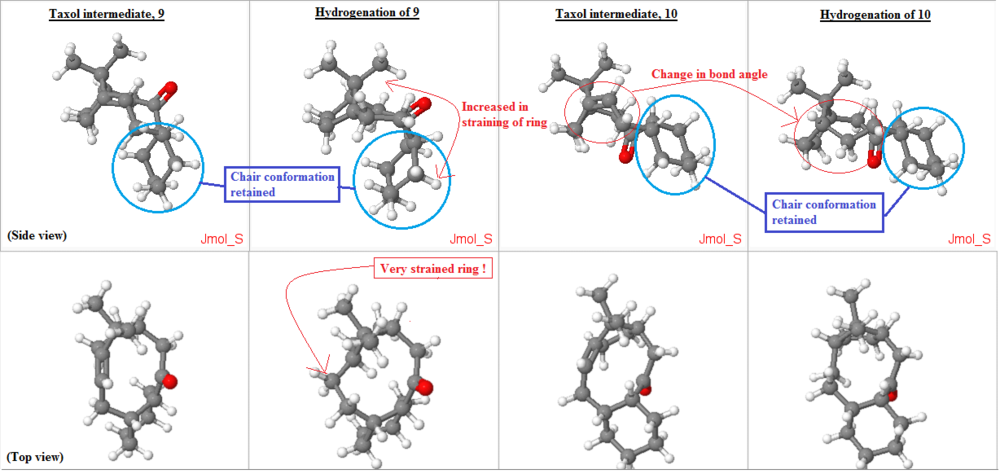
From figure above, all the structures were optimized with their cyclohexane ring in chair conformation to ensure that the overall structure would be in its lowest conformation possible. (circled and labelled in blue). In the hydrogenation of 10, when the sp² carbons in the alkene was converted to sp³ carbons, there was a change in bond angle of 120 deg. to 109.5 deg. this reduction in bond angle (as depicted in the figure above with red circle) increases the ring strain of the molecule as the ring need to be existing with smaller bond angle. This is very unfavorable. Thus, resulting in overall increase in the energy of the molecule, making the hydrogenation of the alkene at such bridgehead become unfavorable thermodynamically.

Meanwhile, for the hydrogenation of 9, there was a massive increase in energy of the product! It shows that it is even less favorable to hydrogenate such bridgehead alkene. As from the top view figure, on the "Hydrogenation of 9" column, the change in ring shape induced a even strained ring as can be seen from the figure above the point where the ring have to squeeze a corner out from the original ring due to the change in the sp² carbon to sp³ carbon after hydrogenation. Similar to the previous case, there was a change in bond angle of 120 deg. to 109.5 deg. this reduction in bond angle (as depicted in the figure above with red circle) increases the ring strain of the molecule as the ring need to be existing with smaller bond angle. This is very unfavorable as well. Plus, from the side view, one can spot that the ring has to curve inwards (as shown in the figure above, on the side view, 'Hydrogenation of 9' column), straining the ring even more.

In short, the hydrogenation of these bridgehead alkenes would yield product which is thermodynamically high energy products and thus very unfavourable. These alkenes react very slowly and are also coined as hyperstable alkenes too.

Prediction of the ¹³C and ¹H NMR spectra of a related Taxol intermediate and comparison of the predictions with the measured values reported in the literature.

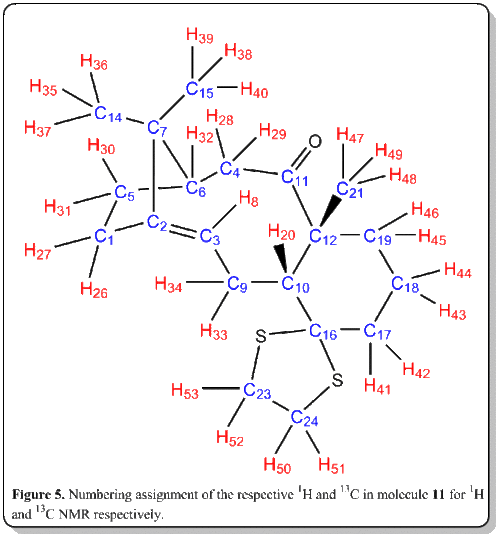
The most useful and rapid technique by far to elucidate the chemical structures would inevitably be Nuclear Magnetic Resonance (NMR). Thus, now we would place computational chemistry in simulating NMR to a test. The ¹H and ¹³C NMR spectrum of molecule 11 was simulated DOI:10042/26522 and compared with literature values. The objective of this comparison was to verify how well the simulated spectra compared to the 'real' spectra, as well as to compare with literature and check on whether the literature values has been correctly interpreted and assigned.

Computational analysis of 11 was executed with the Avogadro program. They were optimized by means of the MMFF94(s) force field option. The alogrithm used was the conjugate gradient option as this evaluates the value of the diagonal terms only while setting all the others to zero. Though it is slower than the steepest descent option, but it assuages the vacillation when reaches less 'steep' gradient where in the steepest descent option, it is very fast but suffer from the vacillation upon reaching less 'steep' gradient. The results and conformation of the computed values are summarized below:

Data of Molecule 11 MMFF94(s) calculation.

Types of Total Energy	Molecule 11/ kcal mol-1
TOTAL BOND STRETCHING ENERGY	16.14072
TOTAL ANGLE BENDING ENERGY	44.81234
TOTAL STRETCH BENDING ENERGY	0.76034
TOTAL TORSIONAL ENERGY	12.24163
TOTAL OUT-OF-PLANE BENDING ENERGY	1.05562
TOTAL VAN DER WAALS ENERGY	59.62994
TOTAL ELECTROSTATIC ENERGY	-7.80810
TOTAL ENERGY	126.83249
Model	Endodimer

Later, the ¹H and ¹³C NMR spectra were simulated with the following procedure. Gaussian was employed to calculate the geometry at the density functional level (DFT) from Avogadro. The calculation was done with the command of Geometry optimization, using B3LYP theory with 6-31G(d,p) basis set. The solvation model was using SCRF(CPCM, Solvent=chloroform).

The results of the computed NMR spectrum is as shown below:

¹H NMR

Simulated ¹H NMR of molecule 11

Simulated ¹H NMR of molecule 11(expanded from 0 - 3.5 ppm)

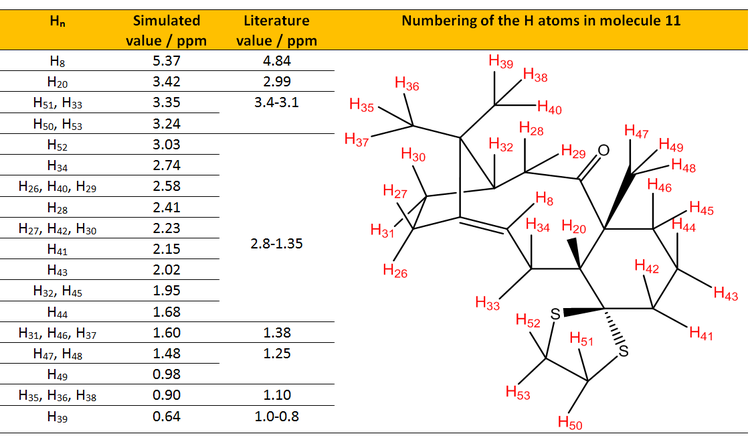
Table 1. Table shows the comparison of assigned simulated ¹H NMR values with the literature values.

From Table 1, all of the simulated ¹H NMR values were higher than of the reported in experimental value. This could be attributed to the basis set being employed for the calculation which is quite a fundamental (or coarse) basis set and thus lead to the fundamental deviation of the NMR being simulated. The basis set being employed in current calculation was B3LYP/6-31(d,p). As most basis set of quantum chemistry were well-developed for valence electron, NMR on the other hand deals with the electron density closer to the nuclei where causes the current calculation having such error. Also, Malkin had also given explanation on the deviation which will be discussed in the ¹³C NMR section.
Analysis of the chemical shifts of simulated NMR. From the literature, Paquette could only observe a 'bunch' of multiplet in the region from 2.8-1.35 ppm while from the simulated spectrum, we are able to assign it to the individual peaks to individual hydrogens. Again we could observe that the range of the simulated NMR for the protons within the region were all slightly higher than of the literature. The range of simulated NMR was 1.35 ppm while for the literature was 1.45 ppm. From the consideration of the range, the simulated spectrum correlated quite well with the literature. H₈ and H₂₀ are protons that are worth analyzing. Both of the values deviated by 0.53 ppm and 0.43 ppm respectively from the literature. This again is attributed to the protons being close to heavy atoms such as sulfur which was not taken into account from the calculation for correction and leading to the deviation. H₈ is also highly deshielded (about 5 ppm due to it being an alkene proton) relative to other protons, which is a sensible result and assignment from the both simulation and literature. Other than that, it could be seen that chemical shifts of terminal CH₃ protons are not all identical in simulation while in experimental results, they are all identical. This was because in real life NMR experiments, the three protons are rotating about the C-C bond and thus making them to be present in similar chemical environment, consequant to one chemical shift observed only. However, in our simulation, we are able to specifically 'label' and 'fix' the protons at certain coordinates and thus making them not in the same chemical environment. As such, we could see from H₄₇, H₄₈ and H₄₉ having different chemical shifts (1.48ppm and 0.98 ppm) in simulation; while in literature, we could obtain single chemical shift which is 1.25 ppm.

Spin-spin couplings of the ¹H NMR

Also, the spin-spin couplings of the ¹H NMR was computed as well. Although advances in electronic structure theory (i.e. equation-of-motion coupled cluster theory, second-order polarization propagator approximations) would enable us to predict spin-spin coupling constants with excellent agreement with experimental values, the calculation or computational costs for these methods would be quite costy when it comes to large systems. Thus, we would employ the density functional theory (DFT) method as it is less expensive and relatively quite accurate. For the current study, we have employed the following keywords to execute the calculation:

 Basis set: B3LYP/6-311+G(d,p) 
 Solvent : SCRF(CPCM,solvent=chloroform) 
Job:  NMR(spinspin, mixed).

The results of the calculation is shown in the DOI link below:
DOI:10042/26640

Data of Simulated coupling constants for ¹H NMR calculation.

nJX-Y	Coupling constant (Simulation), nJX-Y / Hz	Coupling constant (Literature), nJX-Y / Hz	Percentage difference from literature. / %
3JH8-H33	11.0	7.2	53%
3JH8-H34	8.8	4.7	87%
3JH20-H33	7.4	5.2	42%
3JH20-H34	11.7	6.8	72%

Table 2. Data of Simulated coupling constants for ¹H NMR calculation.

From Table 2, we observe that the spin-spin coupling constant has an extremely massive percentage error from the literature value, up to 87%! This could be attributed to the effect of the spin-orbit effect due to heavy atoms that is not taken into account in the current calculations as our current basis set is not sufficiently to produce a reasonable value and corrections were not being made with respect to the effect. Deng also suggested some modification for calculation of NMR spin-spin coupling constant, where we could employ in our calculations in the future. However, as we proceed to smaller systems such as styrene oxide and methyl-strene oxide in following discussions, we could observe that the simulated values matches quite well with the literature.

¹³C NMR

Simulated ¹³C NMR of molecule 11

Simulated ¹³C NMR of molecule 11(expanded from 20 - 250 ppm)

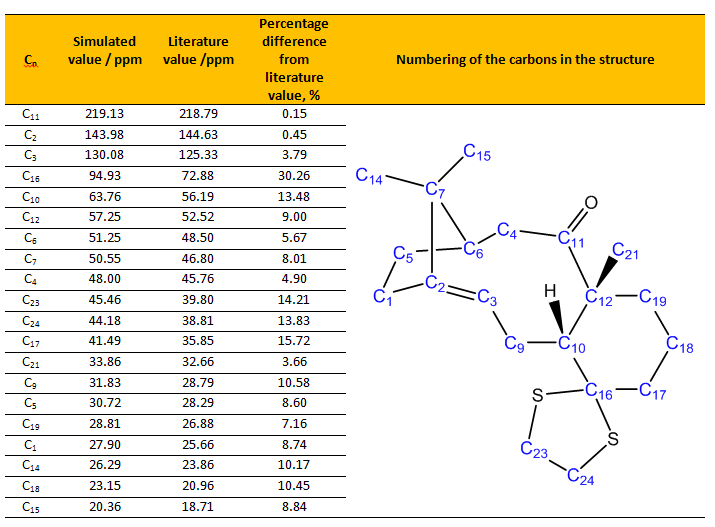
Table 3. Table shows the comparison of assigned simulated ¹³C NMR values with the literature values.

From Table 3, most of the simulated ¹³C NMR values have around 0-10% percentage difference from the literature value, where the simulated values are always slightly higher than literature or experimental values. This could be attributed to the factor as discussed before, where the NMR probes more to the core electron density, we instead deal with valence electrons for quantum chemistry basis set. Besides that, Malkin had studied extensively on the simulated NMR values and found that we should also take into account of relativistic effects for transition metal complexes and any systems containing heavy elements (i.e. Cl, I, S and etc) when doing our calculations. The relativistic effects could be categorized into two types, namely scalar and spin-orbit (SO) effects. As NMR parameters depend strongly on the electronic structure near the nucleus of interest, the NMR parameter would be affected by the relativistic effects much rapidly than other properties such as molecular geometries. Thus Malkin had suggested solutions for to correct for the relativistic effects, particularly SO effect which is quite prominent in current study.

There were some simulated values that have more than 10% percentage difference, and for C₁₆, the difference was up to 30% higher than literature value. Also, C₁₀, C₁₇, C₂₃, and C₂₄ values have more than 10% difference than literature value. This could be attributed to the carbons being attached to "heavy" elements, which in this case sulfur, as described previously by Markin . These carbon bearing sulfur have shifts which needed correction for the spin-orbit coupling errors. C₁₆ has much more deviation than C₁₀, C₁₇, C₂₃, and C₂₄. This is glaringly obvious of the reason behind as this carbon has two sulfur atoms attached to it and thus the spin-orbit coupling error would be much more severe. It is noted that C₂, C₃ and C₁₁ have very high chemical shifts. This is sensible as C₂ and C₃ are alkene carbons while C₁₁ is next to an oxygen atom, thus they have high chemical shifts and most deshielded. Both the simulation and literature agreed well in terms of assigning for these ¹³C NMR shifts.

Comparison of relative energies of two isomeric configurations of 11 and its isomer.

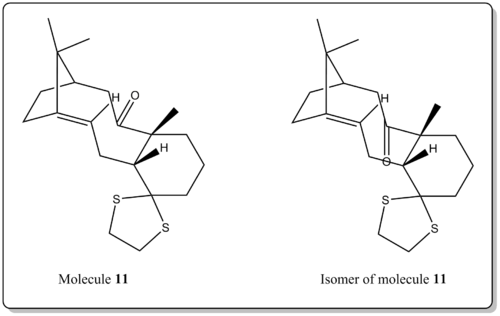
Besides that the free energy, ΔG (Sum of electronic and thermal Free Energies), was computed to compare the relative energies of two isomeric configurations of the molecule 11. (i.e. carbonyl group pointing up or down.)

The results are as shown below:

1) -1651.445143 a.u. (Molecule 11)
Log file: File:Pointingup.log

2) -1651.463260 a.u. (Isomer of molecule 11)
Log file: File:Pointingdown.log

The result is not surprising where when the carbonyl group is pointing down, the molecule is lower in energy, similar to the case of 9 and 10. As explained earlier, it was due to the difference in ring strain imposed on the structure when the carbonyl group is pointing up or down. Also, as there is a thioacetal on the cyclohexane, it locks the cyclohexane into chair form and thus locking the geometry of the larger ring adjacent to it. From our results, it is better when the carbonyl is pointing down as it introduces less strain to the larger the ring due to the constrains in geometry imposed by the adjacent groups of rings.

Part 2

Selected alkenes: styrene and β-methyl styrene.

The crystal structures of Jacobsen's catalyst and Shi's catalyst

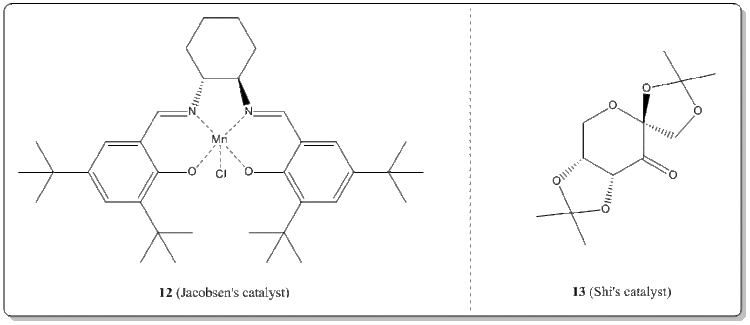
With the Conquest program, the crystal structures of 12 and 13 were searched from the Cambridge Crystal Database (CCDC).

(i) Jacobsen's catalyst, 12.

From Figure 6, at the center of salen ligand (i.e. the two benzene rings bearing ^tBu groups) met head to head, there was a significant close approach of the two adjacent ^tBu groups on the ring ends. Theoretically, when H...H is about 2.4Å apart, they possess van der Waals (dispersion) attraction with each other. Upon reaches about 2.1Å or less, it would then become repulsive instead. For the center part, the hydrogen atoms of the ^tBu have about four close approaches with distances of 2.626Å, 2.421Å, 2.694Å, and 2.636Å. They are considered mildly attractive and not in the repulsive region. These attarctions actually 'closes' the ring and holds the ends of the rings together. On the other hand, within the ring, the ^tBu hydrogens were still far apart from each other to cause any steric clash or to have any significant van der Waals attractions. However, with close inspection, the ^tBu hydrogens have quite a fair amount of van der Waals attractions as well as repulsions with the benzene hydrogen in between the two ^tBu groups of the ring. The repulsive interations were found to be at 1.920Å, and 2.117Å. On the other hand, some moderate attractions span from 2.278Å to about 2.569Å. There were some that were up to 3.320Å which has almost no attractive interactions with the benzene hydrogen atom. Also, it could be seen that the cyclohexane of the salen ligand adopts the chair conformation which is low in energy and is a favorable conformation for the salen ligand. Also, note that at the cyclohexane, the C-N bonds were all in equatorial positions as this is of lower energy conformation as bulky substituents tend to lie at the equatorial position rather than at axial.

It would be intuitive to think that having two bulky groups adjacent to each other in equatorial positions of a cyclohexane chair would lead to steric clash (as shown in figure below). It would be better off for the bulky groups to be in axial to each other to prevent such clash. It is reasonable but due to the templating effect of Mn metal center, the 'ring closure' van der Waals attractive effect due to the close approach of the hydrogen atoms of ^tBu, and having the C=N directing the bulk away from each other due to the sp² N encouraged the two bulky groups to the in equatorial positions.

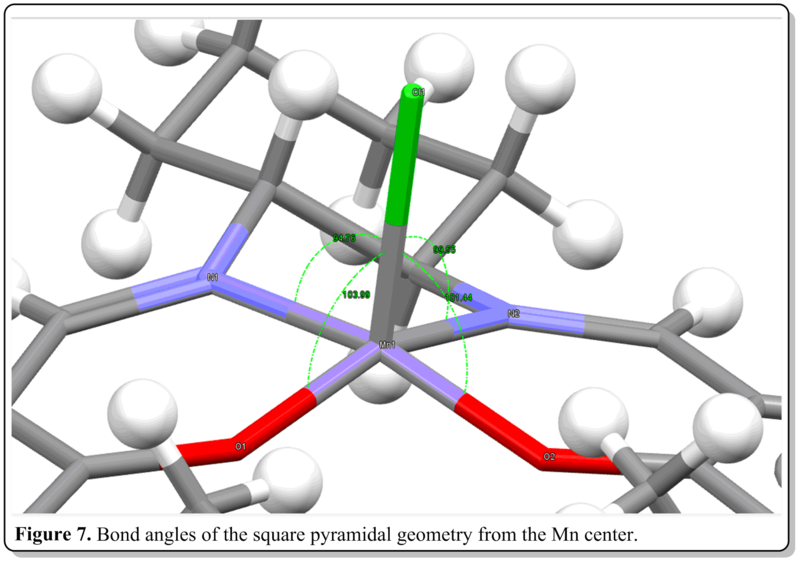
From Figure 7, the bond angles at the metal center is summarized as below:

Bond angle (Cl-Mn-O)= 104 deg., 101 deg.

Bond angle (Cl-Mn-N)= 95 deg., 100 deg.

As inferred from the bond angle data above, the salen ligand, as a whole is not flat nor 90 deg perpendicular to the center Mn-Cl bond, thus it not a perfect square pyramidal structure. However, it is a slightly distorted square pyramidal where the salen ligand curves away from the center Mn-Cl bond, forming sort of like an umbrella got turned inside-out. This distortion was mainly due to sterics rather than electronics reason. This is evident where the central Mn(+3) is d⁴, thus it has no particular advantage to be in either square pyramidal or trigonal bipyramidal structure as the crystal field stabilization energy are quite similar. They both have (d_xz)²(d_yz)² configurations thus is dimagnetic. Also, the structure is a distorted square pyramidal, which, if not due to electronics reason, would be due to sterics reason. Both the distortion and adpotion of the square pyramidal geometry is due to the nature of the salem ligand. The adoption of square pyramidal geometry rather than trigonal bipyramidal structure was due to the salem ligand to be quite planar and having four coordination sites in a planar fashion. If were to maintain the flatness of the ligand when coordinating to four sites without straining the structure, the square pyramidal bearing four coordination sitea at the same plane would be the ideal geometry rather than trigonal bipyramidal having only maximum of three coordination sites being in plane with each other. The distortion could be attributed to the bulky ^tBu groups of the salen ligand. They caused steric clash when the two bulk meet at the center at planar conformation. The middle chlorine atom is also quite huge and electron rich, thus, causes electronic repulsion and repels the bulky ligand away from it. Also, the two imine groups in salem ligand being locked by the cyclohexane also resulted in the distortion. These two groups were holding the two bulky side aromatic rings non-planarly as they are at adjacent to each other at sp³ carbon centers, thus the C-N bonds should be about 109 deg. to one another from the cyclohexane ring.

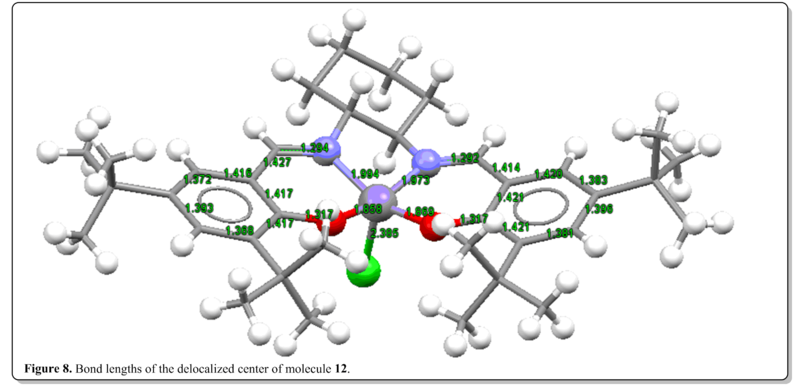
From Figure 8, it could be seen that the CC bond lengths of the delocalized framework (the bonds with the bond lengths labelled) were about 1.4Å. Similar to typical benzene C-C bond lengths which is in between 1.3Å (C=C) and 1.5Å(C-C). This shows that the delocalization is present throughout the Salen ligand framework. Also, it is worth noting that Mn-Cl has longer bond length then Mn-O and Mn-N. This could be rationalized that Cl is larger in size than O and N and thus resulting in longer Mn-Cl bond length.

Bond length (Mn-O)= 1.858 Å, 1.869 Å

Bond length (Mn-N)= 1.994 Å, 1.973 Å

Bond length (Mn-Cl)= 2.385 Å

(ii) Shi's catalyst, 13.

From Figure 9, it is worth noting that O2-C9 and O1-C9 has bond length of 1.454Å and 1.423Å respectively. On the other hand, C2-O2 and C1-O1 should be of the same length as well but they have 1.423Å and 1.429Å, This arrives to an interesting observation as they should in principle be the same bond length. Also, the O2-C9 bond length is actually slightly longer than of ordinary C-O bond length. As reported by Glockler, typical ether C-O bond is 1.420Å while typical aldehyde or ketone C=O bond is 1.210Å. So having bond length of 1.454Å is an indication that this bond is significantly weaker than the other O2-C9 bond. We could account this weakening of bond from the analysis of the structure. We could see that the lone pair of O2 is parallel to C2-C3 bond. There is a vacant p_z orbital in C3 that is able to accept this lone pair. AS the bond in a whole is not just localized between two atoms but is slightly delocalized around, due to this donation of the lone pair, the O2-C9 has slightly lesser share of electron density between them due to the lost of electron density from the donation of lone pair. Thus, the lesser share constituted to the weakening of O2-C9 bond.

O6-C2 bond length is also significantly shorter than ordinary C-O bond, having bond length of 1.415Å which suggested it having slight double bond character. This is due to the O6 having an axial lone pair that is able to be donated to the sigma* orbital of C2-O2 which is axial too (forming pi interaction)and as it is sigma* orbital the lobe is directing away from the C2-O2 bond itself and thus able to accept the electrons from the lone pair. This resulted in the slightly double bond character of C2-O6 bond. Also, population of the sigma* orbital causes the C2-O2 bond length to lengthen by about 0.002Å than normal C-O bond.

C6-O6 does not have such short bond length as observed for O6-C2 (1.434Å). This is because although the sigma* of C-H could be assumed to be able to accept the axial lone pair, forming pi interaction, the energy level might be higher and not really a good acceptor, as contrasted by the C-O sigma* which has the electronegative oxygen, pulling the overall energy level down, making it a good acceptor at sigma* level. Thus, the absence of such good acceptor sigma* orbital does not gain the same double bond character as the previous case.

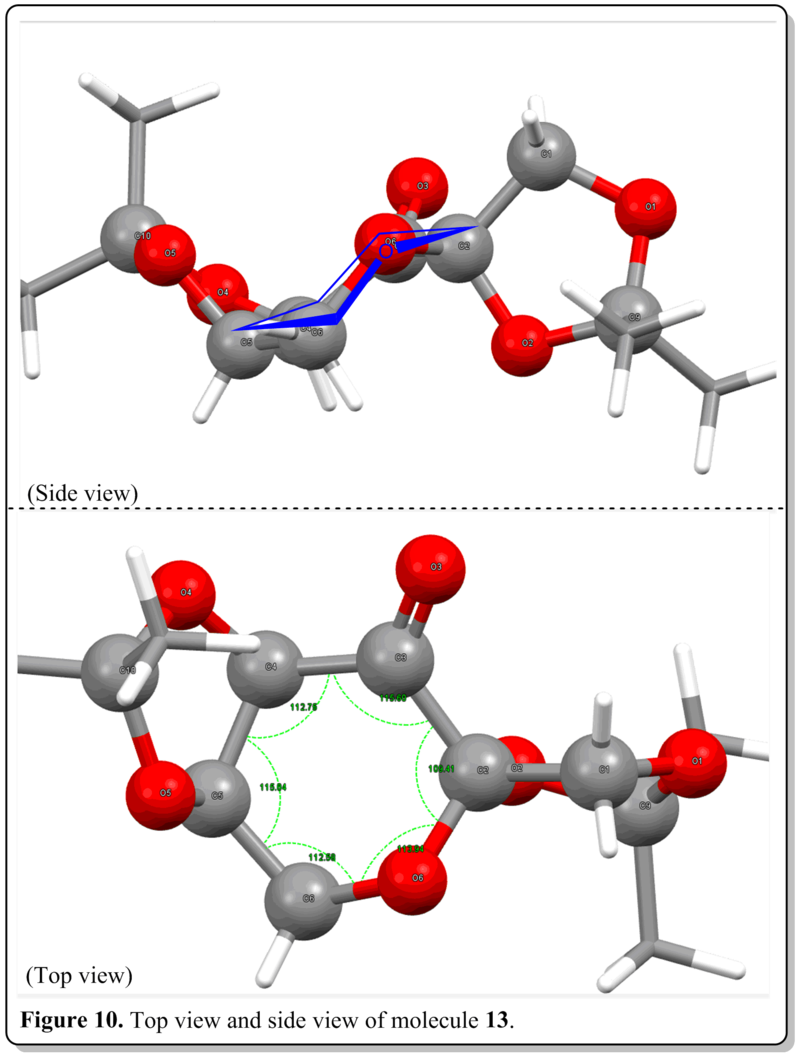
From Figure 10, from the side view, we could see that the central six-membered ring adopts a chair conformation which is a favourable conformation and lowest in energy conformation. Also, from the top view, we could see that for a perfect chair six-membered ring, the internal angle should be 109 deg. as all the ring atoms would be sp³ hybridized. However, as the ring is made up of a mixture of atoms and with substituents at the side of the ring, the internal angles were altered to about 112 deg to accomodate these factors in. It was worth noting that C-O-C bond angle is larger among all the internal bond angles with sp³ oxygen atom and having two lone pairs being the 'substituents'. This could be attributed to the size of the oxygen atom is larger than carbon atom, thus it needs to sustain slightly more bond angle to 'fit' itself in the ring.The bond angle with the carbonyl carbon has the largest bond angle (116 deg.)due to the sp² nature of the carbon that would tend to maximize its bond angle to as close as 120 deg. as possible. Yet, the C₃-C₂-O₆ bond angle, where the C₂ has an acetal group, bearing the smallest bond angle (109 deg.) where it remained the same as postulated for a chair cyclohexane ring. This anomaly in bond angle than others could be due to it being beside a carbonyl carbon and an adjacent oxygen atom which both occupied larger bond angles, leaving the ring system to be able to allocate smaller bond angle to it only without straining the ring more.

Assigning the absolute configuration of the product

(i) Optical Rotation (OR)

Optical rotation (OR) is one of simplest and easiest methods to characterize a certain chiral molecule. Usually there is no correlation for the quantitative value of OR with certain configuration either R or S of a compound. With the advancement in computational chemistry, we would be able to elucidate or at least have an alternative method to be able to predict the OR of a molecule and from then, hopefully study on the factors determining the OR of chiral molecules.

For our current study, we are using density functional theory (DFT) in the OR prediction. Usage of DFT allows us to perform the calculation at a lower cost compared to other methods and having results with accuracy comparable to correlated wave function methods. In terms of basis set selection, Autschbach also stated that the quality of the basis set is utmost crucial in OR calculation and he suggested that it is vital to incorporate diffuse functions in the basis set. This would allow us to obtain results with a relative median error of c.a. 30%. Thus the OR calculations was executed following from the output of the NMR calculation job. The OR calculation was performed with teh following command:

Basis set: CAM-B3LYP/6-311++g(2df,p) 
Polarity: polar(optrot) 
Solvent model:scrf(cpcm,solvent=chloroform)
Job type: CPHF=RdFreq <br> Frequencies: 589nm 365nm

(a)(R)-(-)-Styrene oxide, 14 and (R)-(-)-Styrene oxide, 15

Figure 11.Comparison of the computed OR values (black color font) and literature OR values (blue color font) of 14 and 15.

OR log files for 14 and 15 Log file for 14: File:Moleculefourteentyr.log Log file for 15: File:Moleculefifteentyr.log

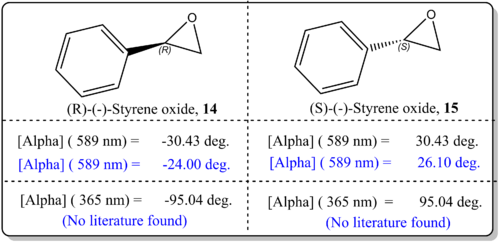
From Figure 11, it was shown that the simulated values agreed well with the literature value. There was just difference by about 6 deg. which indicated that the results are quite reliable. This could be attributed to the basis set being employed for current study CAM-B3LYP/6-311++g(2df,p) which is quite sophisticated. However, Hedegard reported that the best basis set for use with optical rotations is aug-pcS-1, together with the CAM-B3LYP functional which could improve in the calculations. We should also note that the slight deviation from the reported experimental values for OR could be due to the phase model being used in the simulation and experimental values. In the real experiemnts, the OR is taken from the condensed phase, while our computational results refer to gas phase conditions. As such, Kumata had exemplified had shown that the effect of solvation had become severe.

(b)(1R,2R)-(-)-1-Phenylpropylene oxide, 16 and (1S,2S)-(-)-1-Phenylpropylene oxide, 17

Figure 12.Comparison of the computed OR values (black color font) and literature OR values (blue color font) of 16 and 17.

OR log files for 16 and 17 Log file for 16: File:Moleculesixteentyr.log Log file for 17: File:Moleculeseventeentyr.log

From Figure 12, it was shown that the simulated values agreed well with the literature value. There was just difference by about 4 deg. to 0 deg. which indicated that the results are very reliable. This, similar to the previous case could be attributed to the basis set being employed for current study, CAM-B3LYP/6-311++g(2df,p), which is quite sophisticated. We could enhance on the results by using the method as proposed by Hedegard where he employed the basis set aug-pcS-1, together with the CAM-B3LYP functional for OR calculation. We should also note that the slight deviation from the reported experimental values for OR could be due to the phase model being used in the simulation and experimental values. In the real experiemnts, the OR is taken from the condensed phase, while our computational results refer to gas phase conditions. As such, Kumata had exemplified had shown that the effect of solvation had become severe.

(ii) Vibrational circular dichrosim (VCD)

Calculations have been executed on 14 and 16. Initial conformational analyses were done with MMFF94s molecular mechanics force field using Avogadro program. Upon the geometry optimization was performed,
Other than that, as experimental VCD spectrums are scarce due to it being instrumentality expensive, no relevant literature could be compared with to determine how well the simulated spectra matched with literature.

Compound 14

Figure 13. VCD of compound 14. (DOI:10042/26730 )

Compound 16

Figure 14. VCD of compound 16.(DOI:10042/26731 )

The calculated NMR properties of compound 14 and 16.

(a) NMR of compound 14.

Note: as the stereoisomer 14 and 15 could not be differentiated in NMR, NMR of 15 was not attempted as it would yield the same result as 14.

¹H NMR of 14

¹³C NMR of 14

The simulated ¹H and ¹³C NMR (DOI:10042/26734 ,DOI:10042/26735 )were compared with the literature values.

Table 4. The simulated ¹H and ¹³C NMR were compared with the literature values.

From Table 4, it could be seen that the simulated ¹³C and ¹H NMR chemical shift values matched very well with the ¹³C and ¹H NMR chemical shift experimental values.

Analysis of ¹³C NMR
From both the simulation and literature, C₄ to C₉ which are carbons in the aromatic ring were assigned with the highest chemical shifts. These chemical shifts are reasonable and can be rationalized from the fact that C₄ to C₉ are carbon atoms in the aromatic rings and due to the delocalization of the electron density around the ring, these atoms are more deshielded and thus have higher chemical shifts.
Meanwhile, C₁ has higher chemical shift than C₂. This is glaringly obvious due to the fact that C₁ has an adjacent aromatic ring which draws electrons to the ring and causing the C₁ is more deshielded than C₂. Besides that, C₁ and C₂ are adjacent to an oxygen atom, thus both has quite high chemical shifts.

Analysis of ¹H NMR
From both the simulation and literature, H₁₃ to H₁₇ which are hydrogens in the aromatic ring were assigned with the highest chemical shifts. These chemical shifts are reasonable and can be rationalized from the fact that H₁₃ to H₁₇ are carbon atoms in the aromatic rings. Due to the delocalization of the electron density around the ring, these atoms are more deshielded and thus have higehr chemicalshifts. From the simulation, we are able to pin point which hydrogen atom has which chemical shift. However, in real NMR spectrum, those hydrogen chemical shifts overlaps and become multiplets in region of 7.3-7.4 ppm.
Meanwhile, H₁₀ has higher chemical shift than H₁₁ and H₁₂. This is glaringly obvious due to the fact that H₁₀ has an adjacent aromatic ring which draws electrons to the ring and causing the H_1o is more deshielded than H₁₁ and H₁₂. Besides that, H₁₀, H₁₁ and H₁₂ are adjacent to an oxygen atom, thus both has quite high chemical shifts.

Analysis of ¹H NMR coupling constants

Data of Simulated coupling constants for ¹H NMR calculation.

nJX-Y	Coupling constant (Simulation), nJX-Y / Hz	Coupling constant (Literature), nJX-Y / Hz	Percentage difference from literature. / %
2JH11-H12	5.6	5.4	4%
3JH12-H10	4.4	4.0	10%
3JH11-H10	1.9	2.5	21%

Table 5. Data of Simulated coupling constants for ¹H NMR calculation.(DOI:10042/26733 )

From Table 5, we observe that the spin-spin coupling constant has extremely close agreement with literature values, as low as 4%! This could be attributed to the spin-orbit effect due to heavy atoms that is not present in the current calculations. This is totally contrast with the former case for compound 11. Our current basis set is sufficient to produce a close value with literature. Deng also suggested some modification for calculation of NMR spin-spin coupling constant, where we could employ in our calculations in the future if were to improve in the calculation. According to Karplus equation, ³J_H-H is a minimum when the dihedral angle of the two hydrogens has dihedral angle of 90 deg. to each other, while maximum is when 0 deg. and 180 deg.For our current results, ³J_H11-H10 is smaller than ³J_H12-H10. This is because the H12-H10 has dihedral angle of 180 deg. while H11-H10 is about 45 deg., thus consequent to smaller ³J value. ²J_H12-H11 is larger than ³J_{H10-H11 and ²JH12-H10 as it is the coupling between two bonds instead of three bonds.}

(b) NMR of compound 16.

Note: as the stereoisomer 16 and 17 could not be differentiated in NMR, NMR of 17 was not attempted as it would yield the same result as 16.
¹H NMR of 16

¹³C NMR of 16

The simulated ¹H and ¹³C NMR (DOI:10042/26736 ,DOI:10042/26737 )were compared with the literature values.

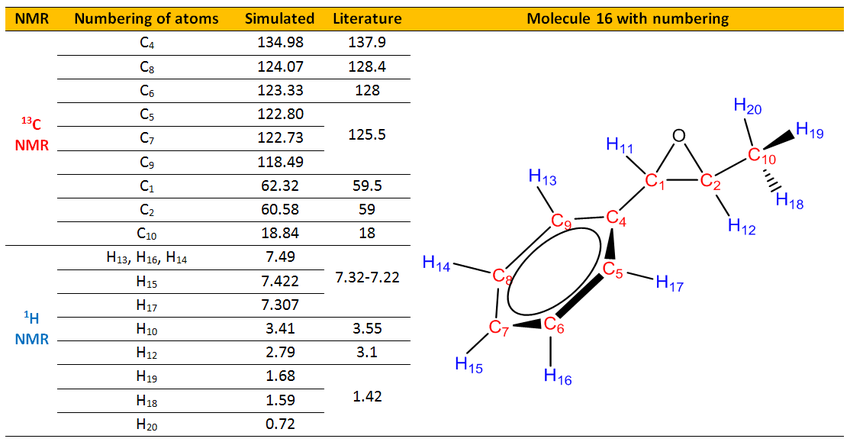
Analysis of ¹³C NMR
From both the simulation and literature, C₄ to C₉ which are carbons in the aromatic ring were assigned with the highest chemical shifts. These chemical shifts are reasonable and can be rationalized from the fact that C₄ to C₉ are carbon atoms in the aromatic rings and due to the delocalization of the electron density around the ring, these atoms are more deshielded and thus have higher chemical shifts.
Meanwhile, C₁ has higher chemical shift than C₂. This is glaringly obvious due to the fact that C₁ has an adjacent aromatic ring which draws electrons to the ring and causing the C₁ is more deshielded than C₂. Besides that, C₁ and C₂ are adjacent to an oxygen atom, thus both has quite high chemical shifts. Other than that, C₁₀ had the smallest chemical shift as it is most shielded. It does not have any adjacent electronegative atoms apart from an oxygen atom which is two bonds away that made it having slightly deshielded than normal terminal CH₃.

Analysis of ¹H NMR
From both the simulation and literature, H₁₃ to H₁₇ which are hydrogens in the aromatic ring were assigned with the highest chemical shifts. These chemical shifts are reasonable and can be rationalized from the fact that H₁₃ to H₁₇ are carbon atoms in the aromatic rings. Due to the delocalization of the electron density around the ring, these atoms are more deshielded and thus have higehr chemicalshifts. From the simulation, we are able to pin point which hydrogen atom has which chemical shift. However, in real NMR spectrum, those hydrogen chemical shifts overlaps and become multiplets in region of 7.22-7.32 ppm.
Meanwhile, H₁₁ has higher chemical shift than H₁₁ and H₁₂. This is glaringly obvious due to the fact that H₁₁ has an adjacent aromatic ring which draws electrons to the ring and causing the H₁₁ is more deshielded than H₁₁ and H₁₂. Besides that, H₁₀, H₁₁ and H₁₂ are adjacent to an oxygen atom, thus both has quite high chemical shifts. As in the simulation, we are able to locate which proton is aat which position, H₁₈, H₁₉ and H₂₀ are all non equivalent and have chemical shift spanned from 0.72 to 1.68 ppm while in the literature it has just one chemical shift of 1.42 ppm due to the rotation of C-C bond that causes the three protons to be equivalent in chemical environment. If were to take the average of H₁₈, H₁₉ and H₂₀ chemical shifts, it was found to have 1.33 ppm. Compared to the literature value of 1.42 ppm, it agreed quite well by having just 0.1 ppm difference. This verified that the limitation of computational chemistry of not being able to locate the hydrogen atoms in same chemical shift and assigned three chemical shifts when there is only one in experimental NMR results.

Analysis of ¹H NMR coupling constants

Data of Simulated coupling constants for ¹H NMR calculation.

nJX-Y	Coupling constant (Simulation), nJX-Y / Hz	Coupling constant (Literature), nJX-Y / Hz	Percentage difference from literature. / %
3JH11-H12	1.4	2.5	44%
3JH20-H12	11.8	5.4	119%
3JH19-H12	3.0	5.4	44%
3JH18-H12	1.4	5.4	74%
3JH(Average 18, 19, 20)-H12	5.4	5.4	0%

Table 6. Data of Simulated coupling constants for ¹H NMR calculation.(DOI:10042/26732 )

From Table 6, we observed that the spin-spin coupling constants simulated have quite bad agreement with literature values, as high as 119%! This is not attributed to the spin-orbit effect due to heavy atoms as shown from previous calculations but from the fact that some geometry features that was not interpreted from the simulation. (c.f. compound 11). Fistly, for ³J_H11-H12, the percentage difference was 44% which is differed by 1.0Hz and it is within the error of the calculation expected. The fact that it is a high 44% was due to the literature coupling constant itself is small and thus a small error would engender high percentage error.

For ³J_H20-H12, ³J_H19-H12, and ³J_H18-H12, the percentage error spanned from 119% to 44%. It was not mainly due to the misleading calculation of percentage error but it has up to 5.0 Hz of error which exceeded the expected error range of 2.0 Hz. When the three values are averaged, instead we have 100% agreement with the literature value of 5.4 Hz. This was because in real NMR experiments, H18, H19, and H20 are all in the same chemical environment due to the rotation about C-C bond. However in the simulation, the rotation was not taken into account and thus producing three distinct coupling constants which should be averaged to obatain an averaged coupling with H12.

Using the (calculated) properties of transition state for the epoxidation using Jacobsen's catalyst and Shi's catalyst to determine enantiomeric excess (e.e.)

Using the “sum of electronic and thermal free energies” from the calculations, which corresponds to the Gibbs Free Energy at 298.15K and 1 atm, the transition state for the expoxidation using two of the catalysts are elucidated quantitatively.

(i) Shi's catalyst

Transition states for Shi epoxidation of trans-β-methyl styrene

Energies for R,R series, ERR /Hartrees	Energies for S,S Series , ESS/Hartrees
-1343.022970	-1343.017942
-1343.019233	-1343.015603
-1343.029272	-1343.023766
-1343.032443	-1343.024742

Transition states for Shi epoxidation of trans-β-methyl styren

Minimum Energy for R,R series, Emin-RR /Hartrees	Minimum Energies for S,S Series, Emin-SS/Hartrees	Difference in the minimum energies, D = Emin-RR- Emin-SS/ Hartrees	Difference in the minimum energies, D = Emin-RR- Emin-SS/ Joules	The ratio of concentrations of the two species, K=exp(-D/RT)	Enantiomeric Excess, ee
-1343.032443	-1343.024742	-0.007701	-20219	3500	99.942%

Transition states for Shi epoxidation of styrene

Energies for R series, ER /Hartrees	Energies for S Series , ES/Hartrees
-1303.730703	-1303.733828
-1303.730238	-1303.724178
-1303.736813	-1303.727673
-1303.738044	-1303.738503

Transition states for Shi epoxidation of styrene

Minimum Energy for R series, Emin-R /Hartrees	Minimum Energy for S series, Emin-S /Hartrees	Difference in the minimum energies, D=Emin-R- Emin-S/ Hartrees	Difference in the minimum energies, D = Emin-R- Emin-S/ Joules	The ratio of concentrations of the two species, K=exp(-D/RT)	Enantiomeric Excess, ee
-1303.738044	-1303.738503	0.000459	1205	0.6148	-23.851%

(ii)Jacobsen's catalyst

Transition states for Jacobsen's epoxidation of trans-β-methyl styrene

Energies for R,R series, ERR /Hartrees	Energies for S,S Series , ESS/Hartrees
-3383.253816	-3383.262481
-3383.254344	-3383.257847

Transition states for Jacobsen's epoxidation of trans-β-methyl styren

Minimum Energy for R,R series, Emin-RR /Hartrees	Minimum Energies for S,S Series, Emin-SS/Hartrees	Difference in the minimum energies, D = Emin-RR- Emin-SS/ Hartrees	Difference in the minimum energies, D = Emin-RR- Emin-SS/ Joules	The ratio of concentrations of the two species, K=exp(-D/RT)	Enantiomeric Excess, ee
-3383.254344	-3383.262481	0.008137	21363	0.00018	-99.964%

Transition states for Jacobsen's epoxidation of styrene

Energies for R series, ER /Hartrees	Energies for S Series , ES/Hartrees
-3343.960889	-3343.969197
-3343.962162	-3343.963191

Transition states for Jacobsen's epoxidation of styrene

Minimum Energy for R series, Emin-R /Hartrees	Minimum Energy for S series, Emin-S/Hartrees	Difference in the minimum energies, D=Emin-R- Emin-S/ Hartrees	Difference in the minimum energies, D = Emin-R- Emin-S/ Joules	The ratio of concentrations of the two species, K=exp(-D/RT)	Enantiomeric Excess, ee
-3343.962162	-3343.969197	0.007035	18470	0.000579	-99.884%

Transition states for Jacobsen's epoxidation of cis-β-methyl styrene

Energies for R,S series, ERS /Hartrees	Energies for S,R Series , ESR/Hartrees
-3383.25106	-3383.259559
-3383.25027	-3383.253443

Transition states for Jacobsen's epoxidation of cis-β-methyl styrene

Minimum Energy for R,S series, Emin-RR /Hartrees	Minimum Energies for S,R Series, Emin-SS/Hartrees	Difference in the minimum energies, D = Emin-RS- Emin-SR/ Hartrees	Difference in the minimum energies, D = Emin-RS- Emin-SR/ Joules	The ratio of concentrations of the two species, K=exp(-D/RT)	Enantiomeric Excess, ee
-3383.25106	-3383.259559	0.008499	22314	0.000123	-99.976%

Shi's catalyst
From the literature forShi's catalyst epoxidation e.e., the e.e. of for R,R-trans-β-methyl styrene oxide were reported to be 92% to 96% which matched well with the simulated value (99.9%). On the other hand, the e.e. of for R-styrene oxide were reported to be 13% to 24% which matched well with the simulated value as well of about 23.9%. This showed that the model for simulation concur with experimental result and is quite reliable in terms of the understanding of the transition state of the reaction.

Jacobsen's catalyst

From the literature for Jacobsen's catalyst epoxidation e.e., the e.e. of for S-styrene oxide was reported to be 46% to 59% which did not match well with the simulated value (99.9%).

On the other hand, the e.e. of for SS-beta-methyl styrene oxide and SR-beta- methyl styrene oxide were reported to be 46% to 59% and 71% to 87% respectively. Which again did not quite match well with the literature value of 99.96% and 99.98% respectively.

This showed that the model for simulation did not concur with experimental result. This could be attributed to computational calculation that was being performed did not include a good enough basis set and thus lead to the deviation. Also, it could be that the transition state that was being modelled was not a true reflection of the real situation and improvement of the modelling should be performed.

Investigating the non-covalent interactions (NCI) in the active-site of the reaction transition state of Shi's catalyst with beta-methylstyrene

The NCI was viewed using (http://www.ch.imperial.ac.uk/rzepa/cub2nci/) and the file to generate the NCI was done using Gaussview.

The NCI gives us information on the electrostatic attractions, hydrogen bonds, and dispersion-like close approaches of pairs of atoms. However, Wu pointed out that the limitation of the NCI analysis was where the noncovalent interactions were characterized just based on one single structure only and in real life, there is geometrical vacillation which was not taken into account. As such, in solutions, the solvent molecules may engender solvation shells, which is crucial in solvation and chemical reactions. Yet, now we are employing NCI analysis for two molecules (the alkene and the Shi catalayst) and investigate on how they interact during the transition state in order to complete the epoxidation.

Figure 16.NCI of transition state of formation of R,R,methyl styrene oxide using Shi's catalyst.

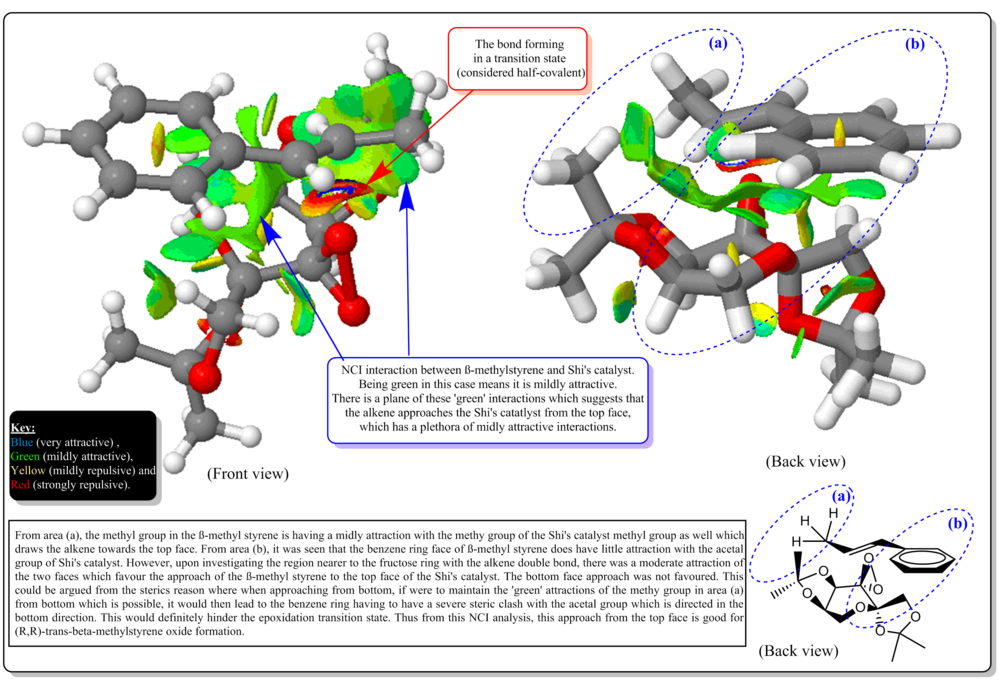
From Figure 16, the general comments on the NCI was annotated and explained. The figure above shows the front view and back view during the transition of the epoxidation. The alkene approaches the catalyst, from the top face (top face defined as in the figure above)). Also, attack underneath is prevented by acetal alkene and approach is directed by anomeric acetal. The alkene is flat and it approaches in the flat face. The resultant epoxide for the transition state above was R,R methyl styrene oxide. It could be seen that, at the face of contact of the alkene and the catalyst, there is a delocalized mildly attractive interaction between them. In the area (a), we could see that the methyl group at the alkene and the methyl group of the acetal group of the catalyst have big mildy attractive (green) interaction that 'sticks' two of them together at that interaction. Besides that, the benzene ring of the alkene and the CH₂ of the acetal group on the other side of the fructose ring have a slight attractive interaction as well that orients the alkene to approach the catalyst at such way. In the red box of Figure 16, we could see the bond forming in the transition state whcih is considered as half covalent. Also, it is noted that in the middle of the benzene ring, there is a midly repulsive interaction. Also, within the Shi's catalyst's, there are a few mildly attractive and repulsive between the side substituents of the frustose ring that could be interpreted as holding the structure of the catalyst at such way shown in the figure and not to swap to other configuration so that the bottom face could be sterically hindered.

Figure 17.Comparing the transition state NCI of RR methyl styrene oxide and SS methyl styrene oxide formation.

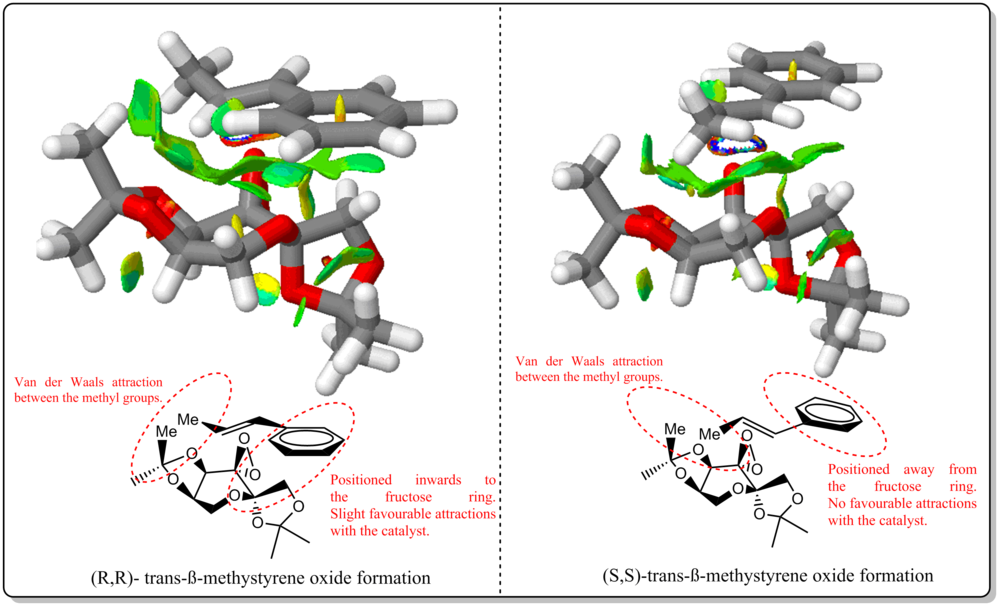
From Figure 17, we could see that there is a significant decrease in the mildly attractive region for the SS formation compared to RR formation. For the SS, the benzene ring of the alkene was positioned away from the Shi's catalyst, constitute to lost in some attractive interactions as compared to the RR formation. For both formations, there are still mildly attractive interactions between the methyl group as annotated in the figure itself. Therefore, as shown from the previous section, for Shi's calatylst, formation of RR over SS epoxide has ee of 99.942% and could be linked from this NCI analysis where due to more attractive interactions present for RR formation at transition state, thus is it more favoured for the alkene to approach the catalyst at such way and yielded the RR enantiomer rather than SS enantiomer.

Investigating the Electronic topology (Quantum Theory of Atoms in Molecules (QTAIM)) in the active-site of the reaction transition site

Bader, introduced QTAIM in order to verify an atom within a molecule and in the context of QTAIM, the free atom is the electron density distribution. In our current analysis, QTAIM is complementary to the NCI (non-covalent) analysis.

Figure 18. Comparison of the QTAIM of RR series and SS series of methyl styrene oxide formation transition state. From Figure 18, focus was given to the Bond Critical Points (BCP) where these points are those yellow dots that are mainly in between the atoms of the molecule (examples are found from the yellow arrow annotation). There are yellow dots in between atoms of different molecules (examples are found from the yellow arrow with a cross annotation)which will be discuss ed later. The BCP present in these two structures are anticipated to be ∇²ρ <0 as from our knowledge, they are bonded covalently. These points are present between all the atoms within a molecule, it shows that there are substantial bonding within the atoms in a molecule. This BCP could be classified as a Shared interaction.

Figure 19. Comparison of the QTAIM of RR series and SS series of methyl styrene oxide formation transition state. The visible 'yellow dots' are weak non-covalent BCPs.

From Figure 19, the top row is the QTAIM of RR series while the bottom row is for the SS series. As shown in the figure, the number of 'yellow dots' between the alkene and catalyst in the RR series is more than of the SS series. There are eight weak non-covalent BCPs (associated with weak interaction between oxygen and hydrogen)in the RR series compared to the SS series, which only have six. This further verified that the formation of RR-beta-methyl styrene oxide is much more favourable due to this difference in the interaction with catalyst.

New candidates for investigations

The new candidate for investigation was carried out using Reaxys with nethyl styrene oxide as a substructure and have the measured (advanced) property ORP.ORP>'500'. This gave a number of hits. However only one was found to be a reasonable compound that the root alkene is commercially available. The chosen epoxide is trans-1-(p-Chlorphenyl)-2-phenylethenoxide.It has [Alpha](436 nm)= 780 deg. Benzene, 1-chloro-4-[(1E)-2-phenylethenyl] could be purchased from | Angene International Limited.