Rep:Mod:yongyao1C
Loh Yong Yao CID 00605583
Part 1: Conformational Analysis using Molecular Mechanics
The dimerization of cyclopentadiene
| Structures |  |
 |
|---|---|---|
| Total bond stretching energy (kcal mol-1) | ||
| Total angle bending energy (kcal mol-1) | ||
| Total stretch bending energy (kcal mol-1) | ||
| Total torsional energy (kcal mol-1) | ||
| Total out-of-plane bending energy (kcal mol-1) | ||
| Total van der Waals energy (kcal mol-1) | ||
| Total electrostatic energy (kcal mol-1) | ||
| Total energy (kcal mol-1) |
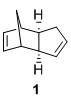
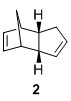
The dimerisation of cyclopetandiene proceeds via a Diels-Alder 4+2 cycloaddition can give rise to two possible products, either 1, the exo product or 2, the endo product. Experimentally, it has been shown that cyclopentadiene dimerizes to give 2 instead of 1. The MMFF94s calculations show that 1 is the actually the more thermodynamically stable isomer relative to 2. Hence, since the thermodynamic product is not obtained, we can say that the dimerisation process is under kinetic control, showing a preference for the endo product. In order to explain this, a closer look at the transition states leading to both products must be analyzed.
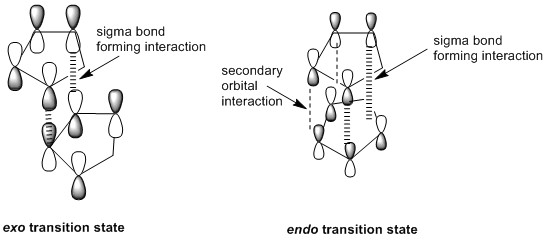
Woodward and Hoffmann attributed this preference for the endo product to secondary orbital interactions, which, in the case of cyclopentadiene dimerization, is the interactions between p-orbitals on both monomers which are not involved in the formation of the two new σ-bonds that are formed in the dimer.[1] The in-phase overlap of these p-orbitals help to stabilize the transition state en route to forming the endo product. These secondary orbital interactions are not present in the exo product. Therefore, the reaction to give the endo product has a lower activation energy and 2 is the favoured product for the dimerization of cyclopentadiene.
The hydrogenation of the cyclopentadiene dimer
| Structures |  |
 |
|---|---|---|
| Total bond stretching energy (kcal mol-1) | ||
| Total angle bending energy (kcal mol-1) | ||
| Total stretch bending energy (kcal mol-1) | ||
| Total torsional energy (kcal mol-1) | ||
| Total out-of-plane bending energy (kcal mol-1) | ||
| Total van der Waals energy (kcal mol-1) | ||
| Total electrostatic energy (kcal mol-1) | ||
| Total energy (kcal mol-1) |
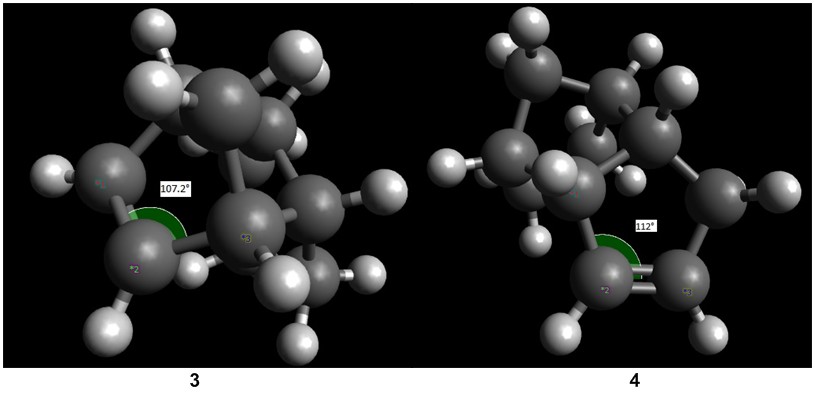
Comparing the two possible products from the mono hydrogenation of the cylopentadiene dimer, the MMFF94s calculations suggest that 4 is the preferred thermodynamic product. This is consistent with experimental observations, as 4 is observed to be formed more readily.[2] Breaking down the energy contributions to the stability of both regioisomers, it can be seen that the greatest differences are in the total angle bending energy (~6.17302 kcal mol-1) and total Van der Waals energy (~2.63712 kcal mol-1).
The two double bonds can be considered to be in very different chemical environments. The double bond present in 3 is a norbornene double bond, and exists in a bicylic environment with a bridgehead. The presence of a double bond in such a constrained environment causes more more strain as the double bond present in 4, which is in a cylclopentene environment. This can be seen by comparing the bond angles as shown in the figure below. The double bond in 4 is less deviated from the preferred 120° for sp2 C as compared to the double bond in 3. Hence, in terms of angle bending energy, 4 is thermodynamically favoured as compared to 3.
Comparing the van der Waals energy between the two regioisomers, there is a favourable attractive H-H van der Waals interaction at a distance of present in 4 that is not present in 3. This is shown in the diagram below. Hence, 4 is further stabilised by this interaction. Therefore, hydrogenation is likely to proceed under thermodynamic control as the thermodynamic product is generated.
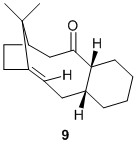
In the total synthesis of Taxol, a key intermediate is known to exhibit atropisomerism.[3] The structures of the two isomers are are shown below and were optimised for comparison and anlaysis. One structure has the carbonyl group pointing up while the other has the carbonyl group pointing down, with one isomer being formed first before isomerizing to the other isomer on standing.
| Structures |  |
 |
 |
|---|---|---|---|
| Total bond stretching energy (kcal mol-1) | |||
| Total angle bending energy (kcal mol-1) | |||
| Total stretch bending energy (kcal mol-1) | |||
| Total torsional energy (kcal mol-1) | |||
| Total out-of-plane bending energy (kcal mol-1) | |||
| Total van der Waals energy (kcal mol-1) | |||
| Total electrostatic energy (kcal mol-1) | |||
| Total energy (kcal mol-1) |
From the values calculated using MMFF94s force field, the thermodynamic product is 10 as it has the lowest total energy. Hence, it is probably the case that in the total synthesis of taxol, 9 is initially synthesized, with the carbonyl group pointing up, and on standing, the compound isomerizes to a thermodynamically more stable isomer 10, with the carbonyl group pointing down. It must be noted that the values obtained are the lowest energy optimisations, with the 6-membered ring in a chair conformation. In the energetic breakdown, the main factor causing the difference in energy is the contribution from the total angle bending energy. This can be attributed to difference in conformation of the 11-membered bi-cycle with a bridgehead caused by the carbonyl group pointing up or down. Hence, from the calculations, we can tell that the ring in 10 is in a more stable conformation as compared to the ring in 9.
It has been experimentally observed that the functionalisation of alkenes such as 10 is slow.[4] This is unusual as it would have been expected that the functionalisation of the alkene to go from an sp2 to an sp3 would be facile due to the relief of ring strain. However, calculations using the MMFF94s force field show that the parent alkane of 10 is of a higher energy (i.e. more unstable). From the breakdown of the energies, we can see that the significant relative destabilisation is the result of two main contributions: angle bending energy and torsional energy. The angle bending contribution suggests that the presence of sp3 carbons in place of the sp2 carbons leads to more strain being experienced. This is evident from the angles measured about the carbon adjacent to the bridgehead. Angles are closer to the preferred 120° for sp2 carbon than to the preferred 109° for sp3 carbons due to the preference for bridgehead groups in medium sized rings to flatten (planarize).[5] The torsional energy contribution is interesting as from looking at the molecule, it does not seem that there is an increase in the number of 1,3-eclipsed groups in the cyclic system.
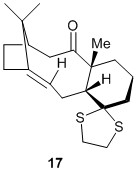
The molecule chosen for this part of the experiment is 17, which was optimised to a minimum energy (with the cyclohexane ring in a chair conformation, before sending for calculations to predict the NMR spectrum of the molecule.
| Structure |  |
|---|---|
| Total bond stretching energy (kcal mol-1) | |
| Total angle bending energy (kcal mol-1) | |
| Total stretch bending energy (kcal mol-1) | |
| Total torsional energy (kcal mol-1) | |
| Total out-of-plane bending energy (kcal mol-1) | |
| Total van der Waals energy (kcal mol-1) | |
| Total electrostatic energy (kcal mol-1) | |
| Total energy (kcal mol-1) |
1H NMR Spectroscopy[6]
| Assignment | 1H Literature NMR chemical shift[7] | 1H Predicted NMR chemical shift |
|---|---|---|
Comparing the reported 1H NMR spectrum for 17 with the one that was predicted based on calculation, we can see that there is a reasonably good match between the 2 spectrums. The vinyl hydrogen is consistently the most deshielded proton in both spectra, however, the predicted spectrum seems to predict a more deshielded proton than what is observed experimentally. The chemical shift reported for the hydrogens on the 1,3-dithiolane ring are consistent with those of the calculated spectrum.
For the rest of the non-methyl hydrogens around the molecule, the -CH2 could be differentiated from the lone hydrogens, forming a distinct region of multiple multiplets in the experimental spectrum , as compared to the lone hydrogens, one of which is significantly more deshielded, forming a multiplet at 2.99 while the other one is more shielded, forming a doublet of doublets at 0.80 - 0.60. However, in the predicted spectrum, the -CH2 peaks overlapped with the dithiolane hydrogens and the lone hydrogens. Also, the range of chemical shifts in the predicted spectrum was much larger than the range in the experimental spectrum. For the lone hydrogens, the chemical shifts differed greatly across the two spectra, and there was no agreement in the relative extent of shielding when comparing the 2 lone hydrogens.
For the methyl hydrogens, the values in both spectra show good agreement. However, as mentioned before, the calculations had to be processed by averaging the 3 values obtained for the methyl hydrogens as the calculation did not take into account the free rotation of the methyl group.
13C NMR Spectroscopy[6]
| 13C Literature NMR chemical shift[7] | 13C Calculated NMR chemical shift (chair) | Difference in chemical shift for chair (lit minus predicted) | 13C Calculated NMR chemical shift (twist boat) | Difference in chemical shift for twist boat (lit minus predicted) |
|---|---|---|---|---|
Comparing the experimental 13C NMR spectra to the predicted one, the two spectra are consistent for the carbonyl carbon as well as alkenyl carbons, with chemical shifts that are highly similar. For the carbon bonded to 2 sulphur atoms in the 1,3-dithialane ring, the chemical shift predicted was much more deshielded than that of the experimental one. The same is observed for the carbon atoms bonded to only 1 sulphur. This is a known issue when predicting the 13C NMR spectrum as carbon attached to heavier elements such as sulphur need to be corrected for spin-orbit coupling errors. However, the actual value of this correction is not known. Comparing the rest of the carbons, only two show a significant difference (>5 ppm difference) between the experimental and predicted spectra. The two carbons in question are one of the methyl carbons on the bridge, and one of the atoms in the cyclohexane ring. It could be possible that the molecule was in the wrong conformation with regards to the cyclohexane ring. A second calculation was done with the cyclohexane ring in the twist-boat[8] conformation instead of the chair conformation. Discounting the C-S carbons, the were two significant differences in between predicted and experimental spectra as well well. However, this time both carbons were part of the cyclohexane ring and one in particular had a large difference of -7.58. Hence, the chair conformation is probably the correct conformation for this molecule.
Conclusion
The experimental and predicted NMR spectra for 17 have some significant differences despite being in general agreement. There are a few possible reasons for this observation.
Firstly, the molecule isolated from the reaction might be in a different conformation as the optimised molecule used for the prediction. This is because although several attempts were made to obtain the minimum energy for the molecule in question by tweaking the conformation of the molecule, the final structure used for the prediction might not be at the global minimum energy. Hence, the experimental molecule, which is presumably at the global minimum, is in a different conformation the different arrangement of the molecules will result in differences in the chemical shift of the hydrogens in the compound. There is also the possibility that the formation of the compound is kinetically controlled, and the experimental sample of the compound is in fact, not in a conformation at the optimised energy minimum.
Secondly, as is evident with the methyl chemical shifts, the calculated spectrum does not take into account the average position of atom. Although only the methyl groups are free to rotate in this highly cyclic molecule, there are other contributions to the fluctuations in atomic position such as vibrational motion, which could, in principle, affect the chemical shift of the molecule.
Lastly, it is possible that the experimental NMR has been slightly wrongly assigned, especially for the lone hydrogens in the 1H spectrum, where it could be difficult to integrate multiplets in a spectrum where the chemical shifts overlap. There could also have been impurities within the sample, which could affect the chemical environment and hence the chemical shift of the molecule.
References for Part 1
- ↑ C. S. Wannere, A. Paul, R. Herges, K. N. Houk, H. F. Schaefer III, P. V. R. Schleyer, "The Existence of Secondary Orbital Interactions", J. Comput. Chem., 2007, 28, 344–61.DOI:10.1002/jcc.20532
- ↑ A. Behr, V. Manz, A. Lux, and A. Ernst, "Highly Selective Mono-hydrogenation of Dicyclopentadiene with Pd-nanoparticles", Catal. Letters, 2013, 143, 241–245.DOI:10.1007/s10562-013-0960-3
- ↑ S. W. Elmore and L. Paquette, "The first thermally-induced retro-oxy-cope rearrangement", Tetrahedron Letters, 1991, 319; DOI:10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0
- ↑ W. F. Maier, P. Von Rague Schleyer, "Evaluation and prediction of the stability of bridgehead olefins", J. Am. Chem. Soc., 1981, 103, 1891. DOI:10.1021/ja00398a003
- ↑ A. B. McEwen and P. v. R. Schleyer, "Hyperstable olefins: further calculational explorations and predictions", J. Am. Chem. Soc., 1986, 108, 3951–3960.DOI:10.1021/ja00274a016
- ↑ 6.0 6.1 Y. Y. Loh, "NMR spectrum for Molecule 17", D-Space, 2014, DOI:10042/28152 Cite error: Invalid
<ref>tag; name "17nmr" defined multiple times with different content - ↑ 7.0 7.1 Spectroscopic data: L. Paquette, N. A. Pegg, D. Toops, G. D. Maynard, R. D. Rogers, "[3.3] Sigmatropy within 1-vinyl-2-alkenyl-7,7-dimethyl-exo-norbornan-2-ols. The first atropselective oxyanionic Cope rearrangement", J. Am. Chem. Soc.,, 1990, 112, 277-283. DOI:10.1021/ja00157a043 Cite error: Invalid
<ref>tag; name "spectra" defined multiple times with different content - ↑ Y. Y. Loh, "NMR spectrum for Molecule 17 (boat)", D-Space, 2014, DOI:10042/28153
Part 2
Crystal Structures of the stable precursors of the epoxidation catalysts
In this section, the crystal structures of the Shi Catalyst precursor, 21 as well as that of the Jacobsen's Catalyst, 23 will be probed. The image below is the crystal structure of 21 obtained from the Cambridge crystal database. Of particular interest for this compound is the 3 anomeric carbons that are present, and using the Mercury program, the C-O bond lengths were obtained.
The anomeric effect is a stereoelectronic effect where in the O-C-O bond moiety, the lone pair of one oxygen overlaps with the σ* C-O orbital of the other C-O bond, forming a pseudo double bond, resulting in bond shortening. This also has the effect of weakening the other C-O bond, which is hence lengthened. Comparing the values of the anomeric C-O bond lengths to the average diether C-O bond length of 1.416 Å[1], we can see that the anomeric C-O bonds in 21 can be grouped into pairs which exhibit the anomeric effect, with one bond shorter and one bond longer than the average "normal" C-O bond. This is shown in the figure below, where a and b form a pair, c and d another pair and e and f as well.
It is interesting to note that searching for the crystal structure of 21 on the cambridge crystal database actually gave two molecules, which suggests that there is a degree of polymorphism in its crystal structure (i.e. the crystal structure is made of more than one type of unit cell). Probing of the C-O bonds in the other molecule gave slightly different values, which suggests the extent of the anomeric effect, which depends on orbital alignment and thus, orbital overlap, can vary.
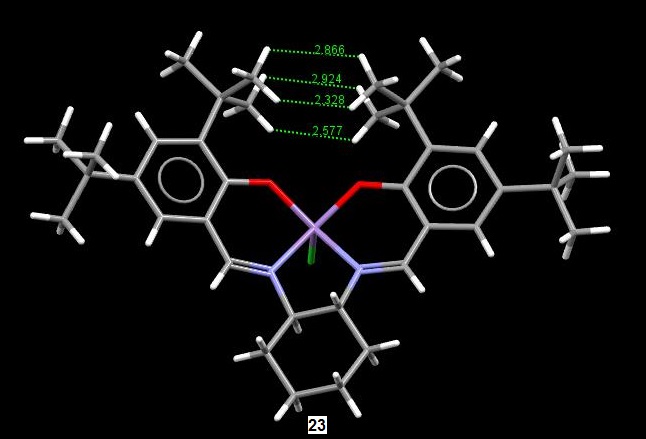
The image below is the crystal structure of 23 obtained from the Cambridge crystal database as well. For this compound, we are interested in the close approach of the two adjacent t-butyl groups on the rings. Using the Mercury program, the distances between the hydrogens were obtained and are shown below. From the distances, we see that there is little steric clash betwen the hydrogens of adjacent butyl t-butyl groups, with the closest distance having a value of 2.328 Å which, is actually in the range for a favourable van der Waals interaction.[2] Again, it is interesting to note that the search results on the Cambridge crystal database for 23 also gave two unique molecules, suggesting polymorphism as well. However, there was one key difference between the two molecules, which was that for one of them, the methyl groups of the t-butyl were conformationally eclipsed, while for the other, they were slightly staggered. However, for the molecule with the staggered conformation, the closest distance between the hydrogens in adjacent t-butyl groups was more than 2.4 Å, which is the limit for favourable van der Waals' interactions. It is possible that the relief gained from having a staggered conformation is offset by the lack of the favourable van der Waals' interaction and vice versa and hence, the reason for polymorphism of the crystal structure.
NMR properties of the epoxides of alkenes
For this part, the two alkenes chosen were styrene and 1,2-dihydronaphthalene. The energies of the alkenes were optimised before being sent for NMR prediction and the energies are summarized in the table below:
| Structures | ||
|---|---|---|
| Total bond stretching energy (kcal mol-1) | ||
| Total angle bending energy (kcal mol-1) | ||
| Total stretch bending energy (kcal mol-1) | ||
| Total torsional energy (kcal mol-1) | ||
| Total out-of-plane bending energy (kcal mol-1) | ||
| Total van der Waals energy (kcal mol-1) | ||
| Total electrostatic energy (kcal mol-1) | ||
| Total energy (kcal mol-1) |
NMR properties of styrene oxide
| 1H Literature NMR chemical shift | 1H Predicted NMR chemical shift | 13C Literature NMR chemical shift | 13C Predicted NMR chemical shift |
|---|---|---|---|
The predicted 1H spectrum[3] shows overall good agreement with the spectra reported in the literature.[4] However, the hydrogens on the aryl ring were predicted to be more deshielded while the rest of the hydrogens were predicted to be more shielded. This could be due to an overestimation of the ring current generated by the aryl ring and an underestimation of the inductive electron withdrawing effect of the oxygen atom. The opposite trend was observed for the 13C spectrum. The aryl carbons were predicted to more shielded while the aliphatic carbons more deshielded compared to the literature.[5] However, the differences are slight and there is good overall agreement between the spectra reported in literature and the predicted spectra.
NMR properties of 1,2-dihydronaphthalene oxide
| 1H Literature NMR chemical shift | 1H Predicted NMR chemical shift | 13C Literature NMR chemical shift | 13C Predicted NMR chemical shift |
|---|---|---|---|
Similar trends were observed for the predicted NMR spectra[6] of 1,2-dihydronaphthalene oxide. Again, in the 1H spectrum, aryl hydrogens were predicted to be more deshielded when compared to the literature.[7] However, there was no real trend for the aliphatic hydrogens this time, with some more shielded while others were more deshielded relative to the literature. For the 13C spectrum, the same trend was observed for 1,2-dihydronaphthalene oxide as in styrene oxide. The aryl carbons were predicted to more shielded while the aliphatic carbons were more deshielded as compared to the literature.[7] However, the differences are slight and there is good overall agreement between the spectra reported in literature and the predicted spectra.
The absolute configuration of the product
Assigning the absolute configuration of the product
The optical rotation for the epoxides of the two alkenes were predicted and compared to literature values. This is summarized in the table below:
| Compound | ||
|---|---|---|
| Optical Rotary Power (Literature) | ||
| Optical Rotary Power (Predicted) |
As can be seen, the sign of the optical rotation for both epoxides match the literature value, which means that they have been correctly assigned. However, the magnitude differs slightly for styrene oxide and quite significantly for 1,2-dihydronaphthalene. This could be due to temperature differences during the measurement, as well as the fact that inaccuracies for reading off larger angles during the experimental measurement of optical rotation are common due to difficulty in establishing the boundaries.
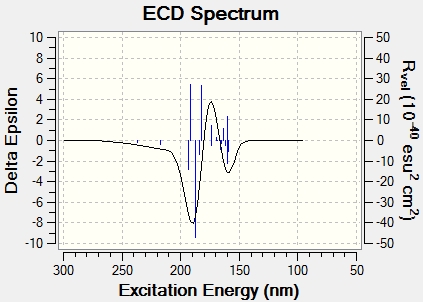
The electronic circular dichroism was also predicted for both molecules and the spectra are presented below.
ECD Spectrum for (S)-styrene oxide[12]:
ECD Spectrum for (1S,2R)-1,2-dihydronaphthalene oxide[13]:
Considering free energy of transition states
Synthesis of styrene oxide and 1,2-dihydronaphthalene oxide using the Shi Catalyst
Considering that a the Shi catalyst used has a fixed chirality, there are 8 possible transition states that are possible for the catalytic epoxidation reaction. The origin of the 8 possibilities are as follows:
1. the alkene can react from either the Re or Si face.
2. there are two possible oxygens from the dioxirane that can be transferred
3. the phenyl group of the alkene can be orientated exo or endo with respect to the fructose in the catalyst
Assuming that the reaction goes through the lowest energy transition state en route to the each enantiomer, the enantiomeric excess for the Shi catalyzed epoxidation reaction can be calculated by taking the difference in energy between the lowest energy transition state for the formation of each enantiomer.
For Styrene Oxide
Free energy difference between S and R transition states, ΔG = -1303.738503[14] - (-1303.738044[15]) = -0.000459 hartree = -1.2051045 kJ mol-1
K = -ΔG/RT = -1.2051045*1000/(8.314*298.15) = 1.62606133
Since K is the ratio of S isomer to R isomer, the enantiomeric excess of S isomer = [(1.62606133 - 1) / (1.62606133 + 1)] * 100% = 23.8%
Hence, there is a calculated enantiomeric excess of 23.8% of (S)-styrene oxide. This is contrary to what is reported in literature, where the enantiomeric excess is determined by optical rotation to give a value of 24%, but for (R)-styrene oxide instead.[16] Hence, there is a calculated enantiomeric excess of 23.8% of (S)-styrene oxide. This is contrary to what is reported in literature, where the enantiomeric excess is determined by optical rotation to give a value of 24%, but for (R)-styrene oxide instead. As can be seen by the low values of enantiomeric excess, it can be deduced that the Shi catalyst does not select well in the epoxidation of styrene, which is a mono-substitued alkene. Indeed, reports in the literature suggest that the enantiomeric excess obtained for the Shi epoxidation is highly influenced by the electronic and steric nature of the alkene substituents. Styrene, with only one substituent, does not allow for easy stereoselection as the differences between the energies of the difference transition states are small. Hence, factors such as the solvent as well as the oxidant used or the pH can have profound effects on the reaction mechanism and the stability of the transition states.
For 1,2-dihydronaphthalene Oxide
Free energy difference between S and R transition states, ΔG = -1381.136239[17] - (-1381.134059[18]) = -0.00218 hartree = -5.72359 kJ mol-1
K = -ΔG/RT = -5.72359*1000/(8.314*298.15) = 10.06434186
Since K is the ratio of S isomer to R isomer, the enantiomeric excess of S isomer = [(10.06434186 - 1) / (10.06434186 + 1)] * 100% = 81.9%
Hence, there is an enantiomeric excess of 81.9% of (1S,2R)-1,2-dihydronaphthalene oxide. This value is much higher as compared to reported values in the literature, where the enantiomeric excess of (1S,2R)-1,2-dihydronaphthalene oxide is only 32%.[19] Again, this can be attributed to the fact that styrene is a mono-substitued alkene with little steric or electronic bulk which does not allow for easy stereoselection as the differences between the energies of the difference transition states are small. Hence, factors such as the solvent as well as the oxidant used or the pH can have profound effects on the reaction mechanism and the stability of the transition states. Hence, differences between literature and predicted values are to be expected.
Synthesis of styrene oxide and 1,2-dihydronaphthalene oxide using the Jacobsen Catalyst
Considering that a the Jacobsen catalyst used has a fixed chirality, there are 4 possible transition states that are possible for the catalytic epoxidation reaction. The origins of the 4 possibilities are as follows:>br>
1. the alkene can react from either the Re or Si face
2. the substrate can be arranged in either endo or exo relative to the catalyst
Assuming that the reaction goes through the lowest energy transition state en route to the each enantiomer, the enantiomeric excess for the Jacobsen catalyzed epoxidation reaction can be calculated by taking the difference in energy between the lowest energy transition state for the formation of each enantiomer.
For Styrene Oxide
Free energy difference between S and R transition states, ΔG = -3343.969197[20] - (-3343.962162[21]) = -0.007035 hartree = -18.4703925 kJ mol-1
K = exp(-ΔG/RT) = -18.4703925*1000/(8.314*298.15) = 1722.07801
Since K is the ratio of S isomer to R isomer, the enantiomeric excess of S isomer = [(1722.07801 - 1) / (1722.07801 + 1)] * 100% = 99.9%
Hence, there is an enantiomeric excess of 99.9% of (S)-styrene oxide. Again this is contrary to the literature value of 65% enanatiomeric excess of (R)-styrene oxide.[22] However, it must be noted that the literature value was obtained using a different ligand in the Jacobsen catalyst. It is highly possible that the subtle change of ligand could have large effects that alter the enantioselectivity of the catalyst completely.
For 1,2-dihydronaphthalene Oxide
Free energy difference between S and R transition states, ΔG = -3421.369033[23] - (-3421.359499[24]) = -0.009534 hartree = -25.031517 kJ mol-1
K = exp(-ΔG/RT) = -25.031517*1000/(8.314*298.15) = 24298.30962
Since K is the ratio of S isomer to R isomer, the enantiomeric excess of S isomer = [(24298.30962 - 1) / (24298.30962 + 1)] * 100% = 99.9%
Hence, there is an enantiomeric excess of 99.9% of (1S,2R)-1,2-dihydronaphthalene oxide. This is contrary to the value obtained in the literature, where an enantiomeric excess of 86% of the (1R,2S)-1,2-dihydronaphthalene was reported.[25] This serves to highlight the limitations of predicting the enantiomeric excess of the reaction. Indeed, this method of prediction makes assumptions about there being only 4 possible transition states, when the alkene, especially a highly planar one like 1,2-dihydronaphthalene, can actually approach the catalyst in a side on fashion, which could have an effect on the enantiomeric excess of the reaction. It is highly possible that there is a lower energy transition for this reaction that has yet to be calculated.
Investigating the non-covalent interactions (NCIs) in the active-site of the reaction transition state
The NCIs of the lowest energy transition state for the Shi catalyzed epoxidation of 1,2-dihydronaphthalene oxide to give (S,R)-1,2-dihydronaphthalene oxide was probed and this is shown in the figure below:
The interactions occurring between substrate and catalyst in the active site are labelled, and the rest of the interactions either occurring within the substrate or the catalyst and do serve to help the reaction proceed. On the whole, there is mildly attractive NCIs between substrate and catalyst and no repuslsive interactions. This is expected as this is the lowest energy transition state.
Investigating the Electronic topology (QTAIM) in the active-site of the reaction transition state
The electronic topology of the lowest energy transition state for the Shi catalyzed epoxidation of 1,2-dihydronaphthalene oxide to give (S,R)-1,2-dihydronaphthalene oxide was probed and this is shown in the figure below:
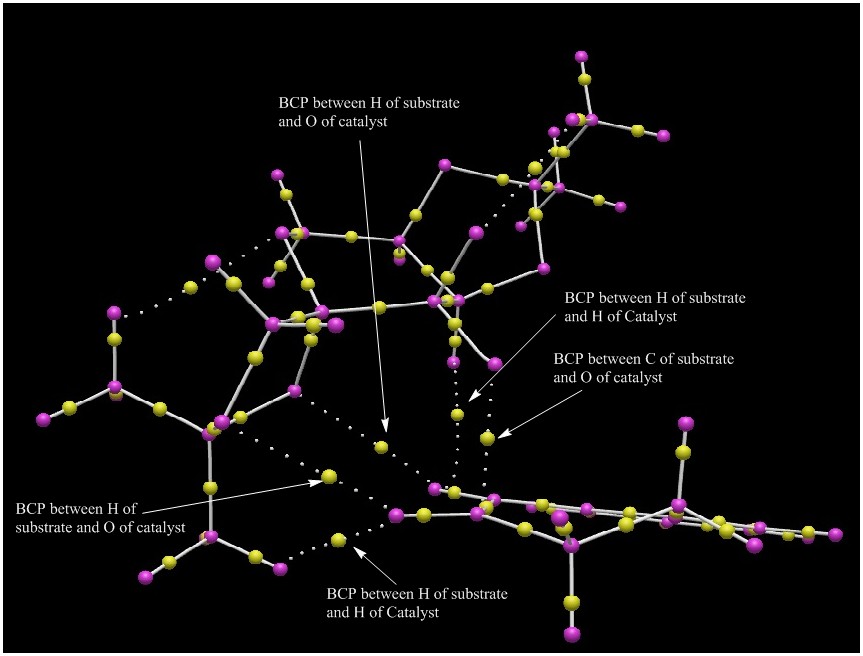
There are some interesting bond critical points (BCPs) that can be seen between the substrate and the catalyst. These have been labelled. None of the BCPs are associated with covalent bonds between the substrate and the catalyst. It is interesting to note that the BCPs between substrate and catalyst are located in the middle of the 2 atoms while the covalent heteroatomic BCPs within molecules are skewed towards one atom, generally the lighter atom. Comparing this to the NCI analysis, there is good agreement as the BCPs occur between the atoms that have NCIs. This shows that QTAIM analysis is a good complement for NCI analysis. However, QTAIM does not differentiate between bond forming covalent interactions and the attractive NCIs.
Suggesting new candidates for investigations
A possible new candidate for investigation is the epoxide methyl 3,4-anhydro-β-L-ribopyranoside. The parent alkene of this epoxide is methyl-3,4-didesoxy-β-L-glycero-pent-3-enopyranosid and they are both shown below:
The epoxide has been shown to have an optical rotary power of 542.8° at 589 nm.[26] However, only one report of the optical rotary power was found and it is possible that it might have been mis-assigned, considering the really high value. A computational study of it would be good to confirm or call into question the reported value.
References for Part 2
- ↑ CRC Handbook of Chemistry and Physics, Internet Version 2005, <http://www.hbcpnetbase.com>, CRC Press, Boca Raton, FL, 2005
- ↑ H. Rzepa, "Favourable Van der Waals' interactions", Conformational Analysis, 2014, DOI:10042/a3uy9
- ↑ Y.Y. Loh, "Styrene Oxide NMR", D-Space, 2014, DOI:10042/28154
- ↑ H. Toda, R. Imae, and N. Itoh, "Efficient biocatalysis for the production of enantiopure (S)-epoxides using a styrene monooxygenase (SMO) and Leifsonia alcohol dehydrogenase (LSADH) system", "Tetrahedron: Asymmetry", 2012, DOI:10.1016/j.tetasy.2012.09.017
- ↑ D. Xiong, X. Hu, S. Wang, C.-X. Miao, C. Xia, and W. Sun, "Biaryl-Bridged Salalen Ligands and Their Application in Titanium-Catalyzed Asymmetric Epoxidation of Olefins with Aqueous H2O2", "European J. Org. Chem.", 2011, "4289–4292", DOI:10.1002/ejoc.201100512
- ↑ Y.Y. Loh, "1,2-dihydronaphthalene Oxide NMR", D-Space, 2014, DOI:10042/28155
- ↑ 7.0 7.1 K. Smith, C.-H. Liu, and G. a El-Hiti, "A novel supported Katsuki-type (salen)Mn complex for asymmetric epoxidation.", "Org. Biomol. Chem.", 2006, "917–27". DOI:10.1039/b517611p
- ↑ H. Lin, J. Qiao, Y. Liu, and Z.-L. Wu, "Styrene monooxygenase from Pseudomonas sp. LQ26 catalyzes the asymmetric epoxidation of both conjugated and unconjugated alkenes", "J. Mol. Catal. B Enzym.", 2010, "67", "236–241."DOI:10.1016/j.molcatb.2010.08.012
- ↑ H. Sasaki, R. Irie, T. Hamada, K. Suzuki, and T. Katsuki, "Rational design of Mn-salen catalyst (2): Highly enantioselective epoxidation of conjugated cis olefins", "Tetrahedron", 1994, "50", "11827–11838". DOI:10.1016/S0040-4020(01)89298-X
- ↑ Y.Y. Loh, "Styrene Oxide Optical Rotation", D-Space, 2014, DOI:[https://doi.org/ 10042/28156 10042/28156]
- ↑ Y.Y. Loh, "1,2-dihydronaphthalene Oxide Optical Rotation", D-Space, 2014, DOI:10042/28157
- ↑ Y.Y. Loh, "Styrene Oxide ECD", D-Space, 2014, DOI:10042/28158
- ↑ Y.Y. Loh, "1,2-dihydronaphthalene Oxide ECD", D-Space, 2014, DOI:10042/28159
- ↑ H. S. Rzepa, "Gaussian Job Archive for C20H26O7", figshare, 2013, DOI:10.6084/m9.figshare.826003
- ↑ H. S. Rzepa, "Gaussian Job Archive for C20H26O7", figshare, 2013, DOI:10.6084/m9.figshare.822137
- ↑ M. Hickey, D. Goeddel, Z. Crane, and Y. Shi, "Highly enantioselective epoxidation of styrenes: implication of an electronic effect on the competition between spiro and planar transition states.", "Proc. Natl. Acad. Sci. U. S. A.", 2004, "101", "5794–8." DOI:10.1073/pnas.0307548101
- ↑ H. S. Rzepa, "Gaussian Job Archive for C22H28O7", figshare, 2013, DOI:10.6084/m9.figshare.832544
- ↑ H. S. Rzepa, "Gaussian Job Archive for C22H28O7", figshare, 2013, DOI:10.6084/m9.figshare.832511
- ↑ M. Hickey, D. Goeddel, Z. Crane, and Y. Shi, "An Efficient Catalytic Asymmetric Epoxidation Method", "J. Am. Chem. Soc.", 1997, "119", "11224–11235." DOI:10.1021/ja972272g
- ↑ H. S. Rzepa, "Gaussian Job Archive for C36H44ClMnN2O3", figshare, 2013, DOI:10.6084/m9.figshare.860441
- ↑ H. S. Rzepa, "Gaussian Job Archive for C36H44ClMnN2O3", figshare, 2013, DOI:10.6084/m9.figshare.860449
- ↑ Y. Jeong, S. Choi, K. Yu, and K. Ahn, "Asymmetric Alkene Epoxidations Catalyzed by Sterically Hindered Salen-Mn(Ⅲ) Complexes", "Bull. Korean Chem. Soc.", 2003, "24", "537–538" DOI:10.5012/bkcs.2003.24.5.537
- ↑ H. S. Rzepa, "C38H46ClMnN2O3", figshare, 2013, DOI:10.6084/m9.figshare.903752
- ↑ H. S. Rzepa, "C38H46ClMnN2O3", figshare, 2013, DOI:dx.doi.org/10.6084/m9.figshare.907332
- ↑ J. F. Larrow and E. N. Jacobsen, "Kinetic Resolution of 1,2-Dihydronaphthalene Oxide and Related Epoxides via Asymmetric C-H Hydroxylation", "J. Am. Chem. Soc.", 1994, "116", "12129–12130" DOI:10.1021/ja00105a094
- ↑ N. Mohal and A. Vasella, "Synthesis of Fusion-Isomeric Imidazopyridines and Their Evaluation as Inhibitors ofsyn- andanti-Protonating Glycosidases", "Helvetica Chimica Acta", 2005, "88", "100–119" DOI:10.1002/hlca.200490287