Rep:Mod:yi11LALB

Year 3 Inorganic Computational Chemistry Lab 3S Part Two

Introduction

According to the IUPAC Gold book of terms, a 'Lewis acid' is a molecular entity that accepts an electron pair and reacts with a Lewis base to form a Lewis adduct^[1] Conversely, a 'Lewis base' is molecular entity that donates a pair of electrons, producing a Lewis adduct.

It is well known that borane, BH₃ is unstable due to its electron deficiency arising from the empty sp² orbital i.e. property as a Lewis acid, thus existing in its more stable dimeric form, diborane B₂H₆.

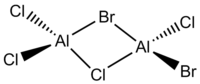
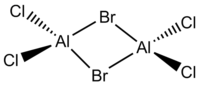
We will investigate whether the same phenomenon occurs with AlCl₂Br and Al₂Cl₄Br₂ via bridging Cl atoms. This has 4 isomers as presented below:

Isomers of Al₂Cl₄Br₂
	A	B	C	D
Structure
Point Group	C_2h	C_2v	C₁	C_2h

Each structure was calculated using GEN basis set and including the keyword 'pseudo=read gfinput' in order to specifiy 6-31G(d,p) basis set for Al and Cl atoms and LanL2DZ pseudo-potential for Br atoms.

Optimisation

Results

Results of the optimisations are summarised below with a link to the LOG file embedded under 'File Type'.

Optimisation Results of Isomers of Al₂Cl₄Br₂
	A	B	C	D
Structure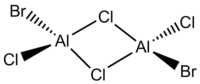
Point Group (Predicted)	C_2h	C_2v	C₁	C_2h
File Name	YI11_Al2Cl4Br2_A_OPT_GEN	YI11_Al2Cl4Br2_B_OPT_GEN	YI11_Al2Cl4Br2_C_OPT_GEN	YI11_Al2Cl4Br2_C_OPT_GEN
File Type	.log	.log	.log	.log
Calculation Type	FOPT	FOPT	FOPT	FOPT
Calculation Method	RB3LYP	RB3LYP	RB3LYP	RB3LYP
Basis Set	Gen	Gen	Gen	Gen
Charge	0	0	0	0
Spin	Singlet	Singlet	Singlet	Singlet
E(RB3LYP) (a.u.)	-2352.41629858	-2352.41626676	-2352.41109943	-2352.40630787
RMS Gradient Norm (a.u.)	0.00001031	0.00001808	0.00003527	0.00002316
Imaginary Frequency
Dipole Moment (Debye)	0.001	0.1674	0.1373	0.0000
Point Group (Outcome)	C1	C1	C1	C1
D-Space link	DOI:10042/25586	DOI:10042/25587	DOI:10042/25588	DOI:10042/25589

Isomer A:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000023     0.000450     YES
 RMS     Force            0.000009     0.000300     YES
 Maximum Displacement     0.000454     0.001800     YES
 RMS     Displacement     0.000196     0.001200     YES
 Predicted change in Energy=-3.705114D-09
 Optimization completed.
    -- Stationary point found.

Isomer B:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000033     0.000450     YES
 RMS     Force            0.000014     0.000300     YES
 Maximum Displacement     0.000850     0.001800     YES
 RMS     Displacement     0.000348     0.001200     YES
 Predicted change in Energy=-2.494165D-08
 Optimization completed.
    -- Stationary point found.

Isomer C:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000081     0.000450     YES
 RMS     Force            0.000022     0.000300     YES
 Maximum Displacement     0.001119     0.001800     YES
 RMS     Displacement     0.000477     0.001200     YES
 Predicted change in Energy=-3.396796D-08
 Optimization completed.
    -- Stationary point found.

Isomer D:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000049     0.000450     YES
 RMS     Force            0.000024     0.000300     YES
 Maximum Displacement     0.001204     0.001800     YES
 RMS     Displacement     0.000649     0.001200     YES
 Predicted change in Energy=-8.889085D-08
 Optimization completed.
    -- Stationary point found.

Geometrical Information of Isomer of Al₂Cl₄Br₂
Geometrical Information		A	B	C	D
Bond Length	Al-μCl	2.30 Å	2.30 Å	2.30 Å	-
	Al-Cl	2.09 Å	2.09 Å	2.09 Å	2.09 Å
	Al-μBr	-	-	2.49 Å	2.49 Å
	Al-Br	2.27 Å	2.27 Å	2.28 Å	-
Bond Angle	μCl-Al-μCl	90 °	90 °	-	-
	μBr-Al-μBr	-	-	-	92 °
	μBr-Al-μCl	-	-	90 °	-
	Al-μCl-Al	-	90 °	93 °	-
	Al-μBr-Al	-	-	85 °	88 °

Relative Energies

Relative Energies of Isomer of Al₂Cl₄Br₂
	A	B	C	D
Structure
Relative Energy (kJmol^-1)	0.00	0.08	13.65	26.23

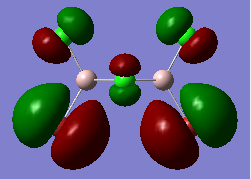
The table above shows that generally, the further the two Br atoms are away from each other, the more stable the isomers are. The reasons to consider are orbital overlap, steric interactions, electronegativity and bond polarity. Isomer A is the most stable with the lowest energy where the terminal Br atoms are trans to each other. This is the best arrangement of atoms as there is minimal steric repulsion, thus not destabilising the molecule. Isomer B where the Br atoms are cis to each other is marginally less stable compared to Isomer A with a relative energy of 0.08 kJmol^-1; they are isomer of each other via rotation of terminal Cl and Br atoms about one of the Al atoms. The images of the HOMOs of Isomers A and B illustrate the large Br orbitals that contribute to the steric interaction. Isomer C is the next less stable being 13.26 kJmol^-1 higher in energy where a Br atom replaces a μ-Cl atom. Cl and Al are in the second row of the periodic table, having optimal orbital overlap and forming strong Al(μ-Cl) bonds as well as AlCl bonds. Replacement of Cl with Br causes the bond length to increase and weaken due to the increased orbital size and decreased orbital overlap. It is worth noting that the decreased electronegativity would decrease the polarity of the bond and increase the bond strength but it may not be the overriding factor. Isomer D is the most unstable being double the energy of Isomer C at 26.23 kJmol^-1 with two μ-Br atoms which weaken the already electron deficient 3c-2e bridging bonds in addition to the highly electron-withdrawing Cl at all terminals of the dimer, thus destabilising the molecule.

Dissociation Energy

The AlCl₂Br monomer was optimised using the same method as the dimer. The results can be found here DOI:10042/25716 .

         Item               Value     Threshold  Converged?
 Maximum Force            0.000200     0.000450     YES
 RMS     Force            0.000133     0.000300     YES
 Maximum Displacement     0.001257     0.001800     YES
 RMS     Displacement     0.000683     0.001200     YES
 Predicted change in Energy=-7.238570D-07
 Optimization completed.
    -- Stationary point found.

ΔE = E(Al2Cl4Br2)- 2E(AlCl2Br) 

   = -2352.4163 - (-1189.3463 x 2) 

   = +26.2763 a.u.

The bond dissociation energy of Al₂Cl₄Br₂ is +68988 kJmol^-1. This indicates that an extremely large amount of energy is required to decompose the dimer to its monomers thus suggesting that the dimeric form is more stable. However the value can be questioned due to its magnitude being off the scale by 2 orders of magnitude relative to standard bond energy.

Frequency Analysis

Frequency Analysis Results of Isomers of Al₂Cl₄Br₂
	A	B	C	D
Structure
log file	Isomer A.log	Isomer B.log	Isomer C.log	Isomer D.log
D-Space link	DOI:10042/25611	DOI:10042/25604	DOI:10042/25601	DOI:10042/25598

Isomer A:

Low frequencies ---   -4.7483   -0.0033   -0.0030   -0.0023    1.7817    2.2205
 Low frequencies ---   18.2008   49.1137   73.0086

Isomer B:

Low frequencies ---   -4.0974   -2.3504    0.0029    0.0033    0.0044    1.4416
 Low frequencies ---   17.1788   50.9303   78.5368

Isomer C:

Low frequencies ---   -2.6513    0.0020    0.0030    0.0030    1.1389    3.1909
 Low frequencies ---   17.1655   55.9552   80.0523

Isomer D:

Low frequencies ---   -5.0207   -4.4749   -3.1539   -0.0018    0.0027    0.0035
 Low frequencies ---   14.9497   63.3650   86.1484

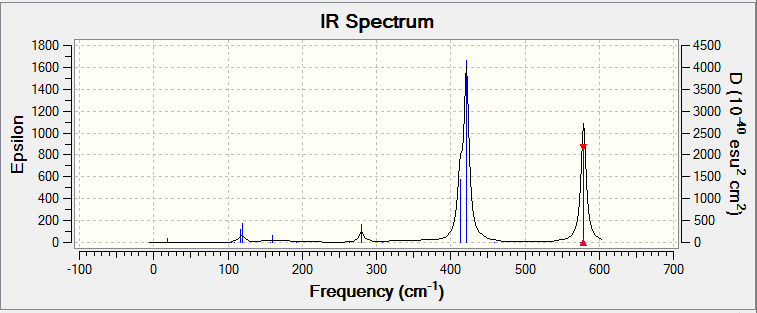
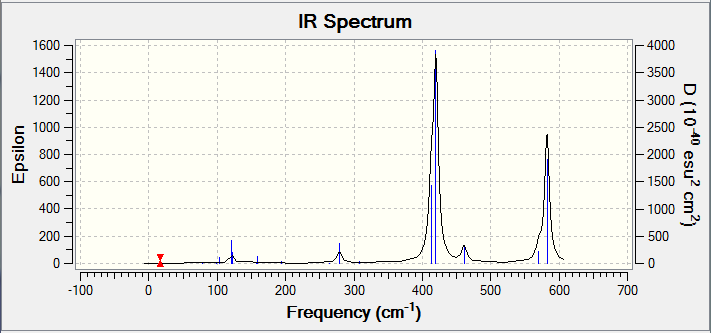
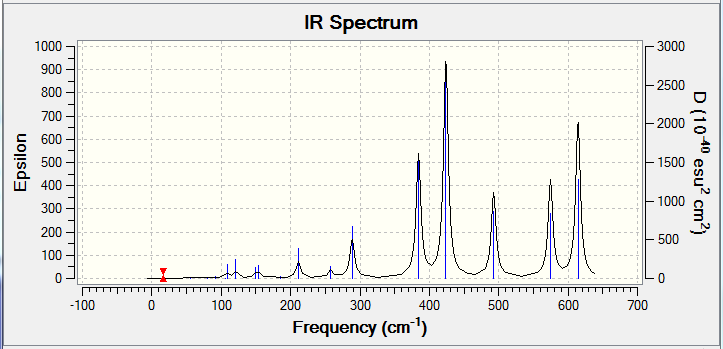
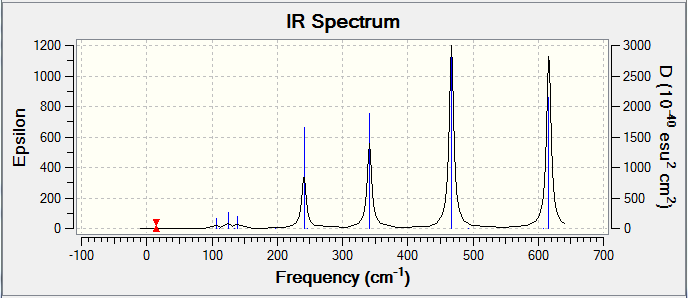
In order to observe a peak in the IR spectrum, there must be a change in dipole moment in that vibrational mode. Stretching modes require more energy than bending stretches however if the stretch is symmetric, there is no overall change in dipole moment and the IR band is inactive. All four isomers possess 18 vibrational modes however differ in the number of IR active ones i.e. spectral peaks.

The IR spectrum of Isomer A has two main peaks with another overlapped at 412 cm^-1, 421 cm^-1 and 578 cm^-1 corresponding to a_u, b_u and b_u symmetry labels respectively when the C_2h symmetry was specified in the frequency analysis OPT.log DOI:10042/25838 FREQ.log DOI:10042/25839 . The Al atoms stretch in and out of the σ_h plane in unison causing a change in dipole moment at 412 cm^-1. At 421 cm^-1 the two Al atoms asymmetrically stretch along the σ_h plane but towards/away from the principle axis whilst at 578 cm^-1 the two Al atoms stretch along the σ_h plane parallel to the principle axis.

The IR spectrum of Isomer B has a similar spectrum to that of Isomer A with three strong intensities with the same types of stretching at 413 cm^-1, 420 cm^-1 and 582 cm^-1.

Isomer C has the most IR active peaks due to its absence of symmetry. Five main peaks are observed at 384 cm^-1, 423 cm^-1, 493 cm^-1, 575 cm^-1 and 614 cm^-1 each with intensities of over 100. The lower three frequencies correspond to stretches discussed in Isomers A and B with the additional influence of the μ-Cl atom as well. At 575 cm^-1, only the AlCl bond with the terminal Br that asymmetrically stretches and the other terminal AlCl stretches at 614 cm^-1. This is in line with the vibrational frequency equation where ν = frequency (cm^-1), k = force constant and μ = reduced mass of the bond because a heavier element will result in a peak at lower frequency due to the inversely proportional relationship of ν and μ.

Isomer D has three active IR peaks at 341 cm^-1, 467 cm^-1 and 616 cm^-1 due to its high C_2h symmetry.

AlBr (Stretching) Vibrations in Isomers of Al₂Cl₄Br₂
Isomer A				Isomer B				Isomer C				Isomer D
Mode	Frequency /cm-1	Intensity	Animation	Mode	Frequency /cm-1	Intensity	Animation	Mode	Frequency /cm-1	Intensity	Animation	Mode	Frequency /cm-1	Intensity	Animation
15	421	438	t-Brs symmetrically stretching	1	18	0	t-Brs rocking	1	17	0	μ-Br wagging and t-Br rocking	1	15	0	μ-Br atoms rocking
16	459	0	t-Brs symmetrically stretching	15	420	35	t-Brs asynchrously symmetrically stretching	3	80	0	μ-Br and t-Br scissoring	3	467	346	μ-Brs twisting
17	574	0	t-Brs asymmetrically stretching	16	461	35	t-Brs synchrously symmetrically stretching	11	211	21	μ-Br asymmetrical stretch and t-Br wagging	9	138	7	μ-Brs wagging
18	579	316	t-Brs asymmetrically stretching	17	570	32	t-Brs asynchrously asymmetrically stretching	15	428	275	t-Br asymmetrical stretch	10	163	0	μ-Brs scissoring

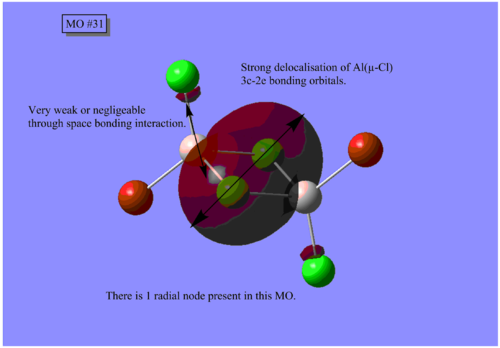
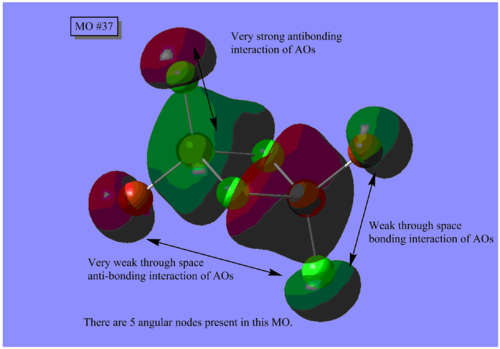
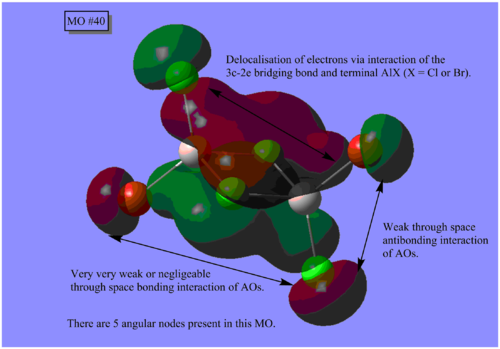
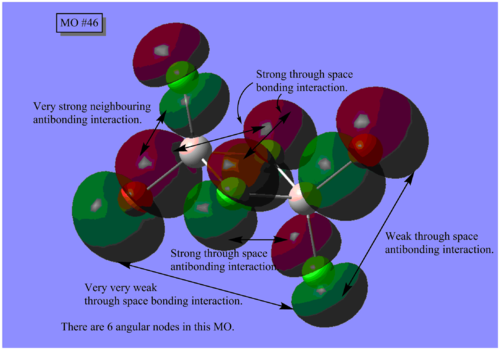
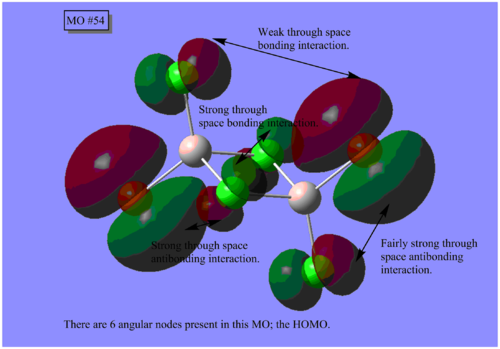
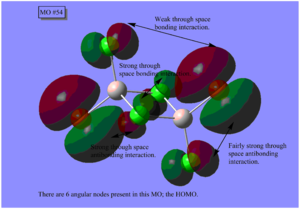
MO Analysis

The results of the MO calculation of the lowest energy isomer, Isomer A are here. DOI:10042/25642

Here are 5 MOs ranging from highly bonding to highly antibonding.

A node is found where there is zero electron density of which there are two types; radial and angular. Radial nodes are found at the centre of an orbital like an s-orbital and angular nodes are found at planes like at the centre of a p-orbital. It can be seen that the number of nodes increases the more antibonding the MOs become and thus higher the energy.

Conclusion

This investigation has found that the isomer of Al₂Cl₄Br₂ with the arrangement of Br atoms in the trans position minimises steric repulsion and is the most stable form which also prefers to remain in the dimeric form as opposed to its monomer.

The most intriguing result came from the optimisation of isomers to reveal the bridging bond angles in Isomer C. It was expected that the Al(μ-Br)Al bond angle would be larger than the Al(μ-Cl)Al to accommodate its size however the outcome was the exact opposite.

References

↑ PAC, 1994, 66, 1077. Glossary of terms used in physical organic chemistry (IUPAC Recommendations 1994) DOI:10.1351/pac199466051077

[1] PAC, 1994, 66, 1077. Glossary of terms used in physical organic chemistry (IUPAC Recommendations 1994) DOI:10.1351/pac199466051077

[1]