Rep:Mod:yhl211phy

Introduction

"A concerted reorganisation of bonding" whereby bonds are formed and/or broken following a concerted transition state is classified as a pericyclic reaction. Major classes of pericyclic reactions includes sigmatropic rearrangements, electrocyclic reactions and cycloadditions. Sigmatropic rearrangements involves a concerted migration of a group whereby one new σ-bond is formed and one σ-bond is broken. The reaction commonly involved a conjugated system but the total number of π- and σ- bonds are unchanged. One of the extensively studied sigmatropic rearrangements is the Cope rearrangement. This exercise aims to perform analysis on the Cope rearrangement with guidance from the laboratory script provided for the module.

The Cope Rearrangement

Figure 1: Scheme for the Cope Rearrangement

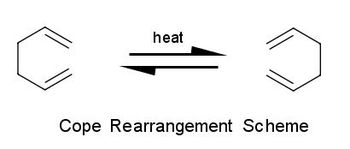
The Cope rearrangement is a [3,3] sigmatropic rearrangement of a 1,5 diene molecule. The reaction mechanism has been debated for a long time but it is currently accepted that the reaction follows a chair or a boat transition state. The preferred reaction mechanism can be determined by using Gaussian to locate the low energy minima and the transition state of the 1,5-hexadiene potential energy surface.

Optimising the Reactants and Products

To study the reaction mechanism, the anti and gauche structure of 1,5-hexadiene was modelled using GaussView 5.0 and then optimised with Gaussian at the Hartree Fock/3-21G level of theory. The low energy conformers with its respective point groups and Newman projections are tabulated below. Another level of theory is available on Gaussian: Density Functional Theory (DFT). This method is treats electron correlation better than the Hartree-Fock method. The transition states were reoptimised using the B3LYP/6-31(d) level of theory to verify the lowest energy conformer.

Possible Low Energy Conformers of 1,5-hexadiene
Conformer	Structure	Newman Projection	Point Group	Energy/Hartree HF/3-21G	Energy/Hartree B3LYP/6-31(d)	Relative Energy	HF/3-21G Log	B3LYP/6-31(d) Log
Anti A			Ci	-231.69260	-234.61180	0.04	Log 1	Log 2
Anti B			C2	-231.69254	-234.61170	0.08	Log 3	Log 4
Gauche C			C2	-231.69167	-234.61069	0.62	Log 5	Log 6
Gauche D			C1	-231.69266	-234.61133	0.00	Log 7	Log 8

Note that conformers anti A and B corresponds to anti 1 and 2 whereas gauche C and D corresponds to gauche 2 and 3 respectively referring to the Appendix 1.

From the table above, gauche C is the lowest energy conformation of the 1,5-hexadiene as proven by two different optimising method. The structure obtained from HF/3-21G and that from B3LYP/6-31G(d) was identical which suggests that the structure is indeed the lowest energy conformation.

The table below records the thermochemistry data of anti B (C_i) conformer. This includes values for their individual electronic energies, the sum of potential energy at 0 K and the zero-point vibrational energy (denoted as sum of electronic and zero-point energies, E = E_elec + ZPE) and energies at 298.15 K and 1 atm including translational, rotational and vibrational energy modes contribution (denoted as sum of electronic and thermal free energies, E = E + E_vib + E_rot + E_trans)

Thermochemistry data for anti B conformer (Ci)
Conformer	Electronic Energy (Hartree)	Sum of electronic and zero-point energies @ 0 K / (Hartree)	Sum of electronic and thermal energies @ 298.15 K / (Hartree)	Calculation Log
Anti B (Ci)	-231.69254	-231.53954	-231.53257	Log 9

Optimising the Transition Structures

Chair Transition Structure

Figure 2: Transition structures for the Cope rearrangement

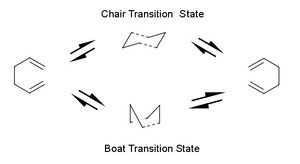
To optimise the chair and boat transition structures, an allyl fragment (CH₂CH₂) was modelled and optimised using the HF/3-21 level of theory. The chair transition state was then postulated by combining two optimised allyl fragments. The terminal carbons were set to a distance of 2.2Å and the structure was optimised using the Opt+Freq function using the TS (Berny) level of theory with the keyword of Opt=NoEigen to prevent the calculation from failing due to a poor guess structure. The calculation yielded a structure with an imaginary frequency of -817.97 cm^-1 (animated as Figure 3) which corresponded to the Cope rearrangement mechanism. This negative frequency proves that the structure obtained was indeed a transition structure and these are discussed in more depth in next section

Figure 3: Imaginary Frequency Vibration Animation

The calculation was repeated using the frozen coordinate method whereby the coordinates of the terminal carbons were frozen using the Redundant Coord Editor function and the rest of the molecule was minimized. The fully relaxed transition state was optimised again without coordinate restrictions, followed by a frequency calculation and its data was compared to that of when the structure was optimised directly.

Figure 4: Front view of the chair transition state

Figure 5: Side view of the TS resembling a chair

The geometries obtained by computing the force constant matrix and that of the frozen coordinate method did not differ. However, the bond breaking/bond forming bond lengths were consistent in the structure obtained from the frozen coordinate method whereas that from computing the force constant matrix directly differed slightly as tabulated below. The more accurate result is probably due to the two step optimisation by the frozen coordinate method which allowed the intermolecular distance to be optimised to a more accurate value in the second step. The results obtained from direct optimisation was similar to the 4^th decimal place which is also as accurate but the other bond length value deviated slightly as the bond distance in the initial guess structure was not exactly the same.

Bond breaking/bond forming bond lengths
	Direct Hessian Optimisation /nm	Frozen Coordinate Method /nm
Bond lengths between C1-C6 / nm	2.02093	2.02063
Bond lengths between C3-C4 / nm	2.02127	2.02064
Difference in bond lengths / nm	0.00034	0.00001
Electronic Energy / nm	-231.61932	-231.61932
Calculation Logs	Log 10	Log 11

Boat Transition Structure

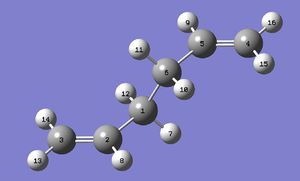
The boat structure was optimised using the QST2 method which will interpolate between the reactant and product structures to determine the transition state. This option searches for the transition structure using the Synchronous Transit-Guided Quasi Newton (STQN) Method which “uses a linear synchronous transit or quadratic synchronous transit approach to get closer to the quadratic region around the transition state and then uses a quasi-Newton or eigenvector-following algorithm to complete the optimization”. The QST2 option requires the reactant and the product to be specified whereby they must be labelled in the same order. Therefore, 1,5-hexadiene was remodelled and the atoms were renumbered from the Atom List as follow:

Figure 6: Relabelled atoms of reactant

Figure 7: Relabelled atoms of products

The structure was then modelled to resemble the boat structure by modifying dihedral and bond angles as the calculation will fail if the structure is not close enough to the transition state geometry. The central four carbons (C-C-C-C) dihedral angle was set to 0° whereas the dihedral angle of both the inside C-C-C’s were set to 100°. The procedure was repeated for that of the product molecule which resulted in the following structures.

Figure 8:Boat transition guess structure for reactant

Figure 9: Boat transition guess structure for product

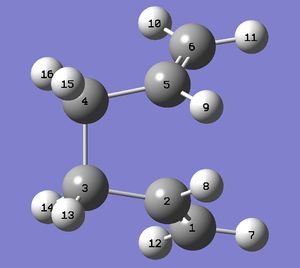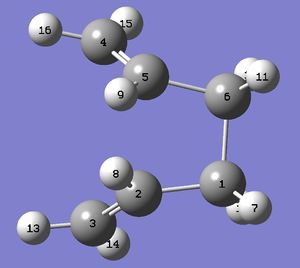The molecules were then optimised to the QST2 level of theory with the HF/3-21G basis set followed by a frequency calculation which then yielded the intended boat transition structure. The imagininary frequency obtained was -839.56 cm^-1 and its vibration was animated as in Figure 12. The energies of the boat transition structure were used to obtain the activation energies and were compared to that of the chair transition structure.

Figure 10: Front view of optimised boat transition state

Figure 11: Side view of optimised boat transition state

Figure 12: Imaginary frequency vibration animation

The energies of the transition states were summarised in the table below. The activation energies were obtained by subtracting the transition state energies with the reactant (anti 2) and converting it to kcal/mol. When optimised with B3LYP/6-31(d) level of theory, the energies increased by approximately 3 Hartree due to the different treatment. The B3LYP treatment appears to be more accurate as it is more similar to the experimental value as compared to the HF/3-21G treatment. The log files for the chair transition state calculation were as before and calculations for the boat transition structures were as follow: Log 12 and Log 13

Thermochemistry data of chair and boat transition states
	HF/3-21G			B3LYP/6-31G(d)
Conformer	Electronic Energy / Hartree	Sum of electronic and zero-point energies @ 0 K / Hartree	Sum of electronic and thermal energies @ 298.15 K / Hartree	Electronic Energy / Hartree	Sum of electronic and zero-point energies @ 0 K / Hartree	Sum of electronic and thermal energies @ 298.15 K / Hartree
Chair	-231.619322	-231.466705	-231.461346	-234.556983	-234.414919	-234.408998
Boat	-231.602802	-231.450929	-231.445300	-234.543093	-234.402340	-234.396006
Anti B	-231.692535	-231.539539	-231.532566	-234.611710	-234.469203	-234.461856

Thermochemistry data of chair and boat transition states
Conformer	HF/3-21G / kcal/mol		B3LYP/6-31G(d) / kcal/mol		Experimental
	0 K	298.15 K	0 K	298.15 K	0 K
Chair TS	45.70	44.69	34.06	33.17	33.5 ± 0.5
Boat TS	55.60	54.76	41.96	41.32	44.7 ± 2.0

Intrinsic Reaction Coordinate (IRC) Analysis

However, the reactive conformer cannot be visually identified from the final optimised transition states. The final step to verify the nature of the conformer is to follow the Intrinsic Reaction Coordinace (IRC) to identify the local minimum on the potential energy surface. This is the minimum energy pathway that connects the reactant, transition state and product at zero kinetic energy. Both the optimised transition state structures were subjected to an IRC calculation whereby the IRC was followed in the forward direction and the force constant was calculated always for N=50 points.

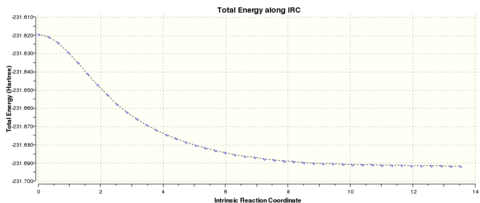
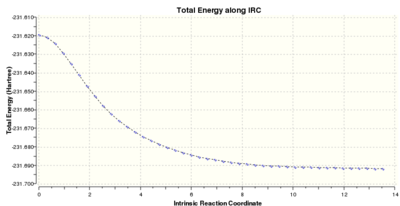
Chair Intrinsic Reaction Coordinate

The N=50 IRC calculation took 44 steps and its energy profile is shown on the below. A conformer similar to that of gauche 2 was obtained but its energy of -231.69158 Hartree (Log 14) was similar but not exactly the same as obtained previously. The calculation was repeated to compute the force calculation at every step for N=150 points (Log 15). However, the energy obtained was the same as before indicating that the number of points was not the limiting factor, also proven when the calculation stopped at 44 steps although the calculationw as set to 50. The last point on the IRC was optimised to a minimum, in which an expected energy value of -231.69166 Hartree (Log 16) was obtained. The geometry of the low energy conformer was confirmed to be a mirror image of the gauche 2 conformer.

IRC Analysis on the Chair Transition Structure
N=50	Final Minimised Geometry	IRC Animation

IRC Analysis on the Chair Transition Structure
N=50	N=100

Boat Intrinsic Reaction Coordinate

The N=50 calculation was completed with 51 steps taken to reach a geometry similar to gauche 3, but it has an energy of -231.68546 Hartree (Log 17). It was observed from the IRC plot that the minimum has not been reached and more points were needed to do so. The calculation was repeated with N=150 points where force constants were calculated at every point to yield an IRC with 75 steps. The geometry was akin to that of gauche 3 but its energy of -231.69262 Hartree (Log 18)was not quite the same. The last point on the IRC was minimised as before to obtain a structure with energy of -231.69266 Hartree (Log 19), same the calculation in the first section. The structure obtained was the mirror image of gauche 3.

IRC Analysis on the Boat Transition Structure
N=50	N=150	Final Minimised Geometry	IRC Animation

IRC Spectrum on the Boat Transition Structure
N=50	N=150

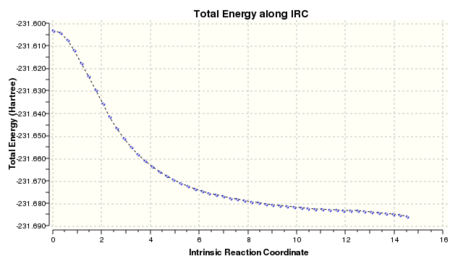
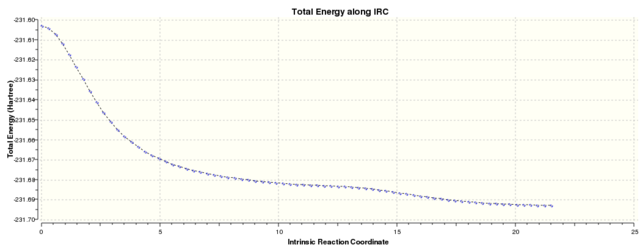
Diels-Alder Cycloaddition

Figure 13: Diels-Alder cycloaddition scheme

A cycloaddition reaction is a pericyclic reaction in which “two or more unsaturated molecules (or parts of the same molecule) combine with the formation of a cyclic adduct in which there is a net reduction of the bond multiplicity" . It is an efficient reaction to construct large rings from its smaller counterparts. One of the most common examples of cycloaddition is the Diels-Alder reaction A thermal reaction involving two π systems, a conjugated diene and a dienophile (often a substituted alkene) is classified as such. The [4+2] cycloaddition results in the formation of a six-membered ring with the formation of two new σ-bonds.

Computing Geometry of Reactants

Molecular Orbitals of Cis-butadiene and Ethene

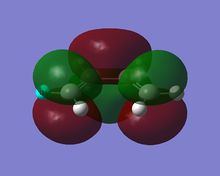
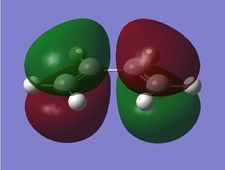
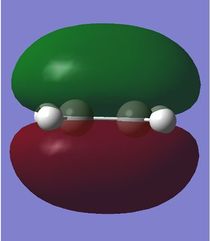
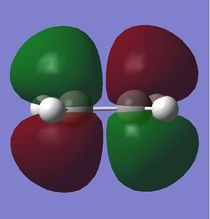
To study the Diels-Alder reaction, the molecular orbitals of cis-butadiene was modelled using GaussView 5.0 and then optimised using Gaussian. The molecular orbitals visualised using Gaussian and it was found that the HOMO of butadiene was antisymmetric and the LUMO is symmetric (Log 20). Molecular orbitals for ethene were also modelled and its HOMO is symmetric whereas its LUMO is antisymmetric.(Log 21) This is as predicted as the HOMO of one reactant has to interact with the LUMO of the other reactant for the reaction to take place, according to the frontier molecular orbital theory. In a Diels-Alder reaction, electron density flows from the higher energy HOMO of the diene into the LUMO of the dienophile as the reaction takes place. The molecular orbitals of both cis-butadiene and ethene obtained using two different basis sets, the semi-empirical AM1 (Log 22 and Log 23)and the HF/3-21G, and were tabulated as below.

The molecular orbitals obtained using two different levels of theory resulted in the same orbitals. This was due to the simple nature of both the reactants which behaved in the same way eventhough it was treated differently. The resulting energies were also different as semi-empirical method calculates using the AM1 Hamiltonian which only considered the valence shell electrons.

Molecular Orbitals of cis-butadiene and ethene
	HF/3-21G		Semi-empirical AM1
Reactant	HOMO	LUMO	HOMO	LUMO
cis-butadiene	antisymmetric	symmetric	antisymmetric	symmetric
ethene	symmetric	antisymmetric	symmetric	antisymmetric

As observed, the bonding HOMO orbital has constructive interactions between C1-C2 and C3-C4 but it has a nodal plane between C2-C3. It is still a bonding orbital due to the dominant constructive interactions. On the other hand, the LUMO is an anti-bonding orbital that has 2 nodal planes, between C1 and C2 as well as C3 and C4.

Energies of cis-butadiene and ethene
Reactant	HF/3-21G / Hartree	Semi-empirical AM1 / Hartree
cis-butadiene	-154.05394	0.04880
ethene	-77.60099	0.02619

Computing the Transition State Geometry

Molecular Orbitals of Transition Structure

Figure 14: Initial guess structure to obtain the envelope transition structure

To study the transition state of the cycloaddition reaction, a starting geometry must be modelled which will be further optimised to resemble the transition structure. A bicyclo system was modelled and optimised after which the CH₂CH₂ fragment is removed resulting in an envelope structure. The terminal atoms were set to 2.20 Å and optimised to a transition state using the HF/3-21G TS(Berny) method (Log 24). The molecular orbitals were plotted as before to characterise the transition state. The structure was also optimised using the semi-empirical AM1 method (Log 25) to compare if it would yield the same results.

The LUMOs obtained from both methods were symmetric and the HOMOs were antisymmetric. This suggests that the reaction is dominated by the butadiene orbitals as the symmetry retained was that of the butadiene orbitals. It was deduced in the above section that the transfer of electron density is from the HOMO of the butadiene to the LUMO of the ethane, as more electrons will result in higher energy orbitals. This is further proven by the retained symmetry of the transition state molecular orbitals. The [4+2] cycloaddition is thermally allowed as the prerequisite for a reaction to occur is for the HOMO and the LUMO of the reactant to have matching symmetry, which is present in this case. A cyclohexene is made with the formation of two σ bonds and a new π bond in the product.

Molecular Orbitals of transition states modelled using HF/3-21G
Reactant	HOMO	LUMO
Front View	anti symmetric	symmetric
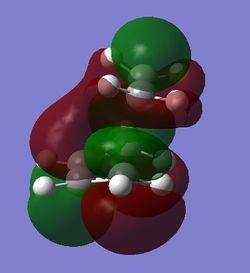
Side View	antisymmetric	symmetric

Molecular Orbitals of transition states modelled using Semi-empirical AM1
Reactant	HOMO	LUMO
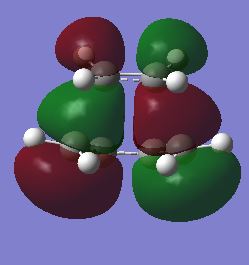
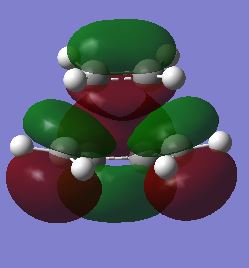
Front View	antisymmetric	symmetric
Side View	antisymmetric	symmetric

Bond Lengths of Transition Structure

Figure 15: Labelled atoms of TS

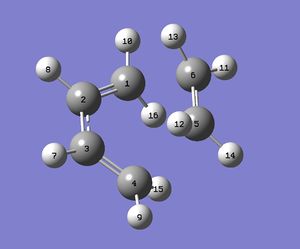
Following the atom labels on Figure 15, the carbon-carbon bond lengths of the optimised structures were obtained for both methods and tabulated below. Although the bond lengths differed slightly in both methods, a trend was still observed from these data. Both the C=C double bonds (C1-C2 & C3-C4) had the exact same lengths while C2-C3 were slightly longer (approximately 0.02 Å) in both cases. However, the C2-C3 bonds were significantly shorter than typical carbon-carbon bond lengths (c.f. 1.547 Å . Cis-butadiene has two conjugated double bonds formed from the overlap of parallel p_z orbitals. Each carbon contributes one electron in an atomic p-orbital which forms the delocalised system thus forming a π interaction across the four carbons which contracted the central C-C bonds.

C5-C6 bond lengths correspond to that of ethane, which is slightly larger than the typical value (1.33 Å ). During the course of the reaction, when electrons from the HOMO of the diene enter the antibonding LUMO orbital of ethane, the bond order decreases and the double bond becomes a single bond. However, these values were computed from a transition state in which the bonds have not been formed and the bond length is still in between that of a double bond and a single bond.

The intermolecular bonds (C1-C6 & C4-C5) are at a distance longer than a typical sp³- sp³ bond length which is expected as the bonds have not been formed in the transition state. It is at a distance shorter than twice the typical Van der Waals radius of carbon (1.77 Å which indicates that there is an attraction interaction at the stipulated site of bond formation, according to the Lennard Jones potential.

Bond lengths of transition state / Å
Carbons	HF/3-21G	Semi-empirical AM1
C1-C2	1.37004	1.38184
C2-C3	1.39441	1.39748
C3-C4	1.37004	1.38184
C5-C6	1.37590	1.38290
C1-C6	2.20934	2.11936
C4-C5	2.20949	2.11925

Vibrational Frequency Analysis

Figure 16: IRC pathway for TS formation

Subjecting the transition state to a frequency calculation, it was observed in the vibrational spectrum that it has one imaginary frequency which confirms that it indeed the transition structure. The imaginary frequency indicates a negative force constant which proves that it is indeed a transition state as stable systems only have real frequencies. The frequency was animated (Log 26) and it did indeed correspond to the reaction coordinate which proves that the correct transition structure was obtained. Furthermore, as observed in the IRC pathway, the formations of the two σ bonds are synchronous. The rocking motion, animated by the lowest positive frequency, does not correspond to the reaction coordinate as there are no observable motions associated with the IRC. This frequency is due to the typical motion observed in the vibrational spectra.

Figure 17: Imaginary frequency animation

Vibrational frequencies of the transition state
	Imaginary frequency / cm-1		Lowest positive frequency / cm-1
	HF/3-21G	Semi-empirical / AM1	HF/3-21G	Semi-empirical / AM1
Vibrational frequency	-818.64	-956.06	166.59	147.24
Animation

Regioselectivity of Diels-Alder reaction

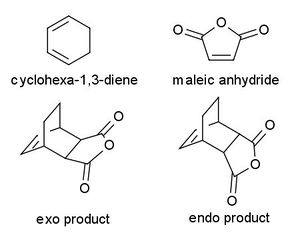
An example of a more complicated reaction is the reaction between cyclohexa-1,3-diene with maleic anhydride whereby the maleic anhydride can orientate in two different ways with respect to the diene. In the exo isomer, the 5-membered ring is orientated farthest away from the bridged carbons and vice versa for the endo form. The reaction was reported to result in the dominant endo product. This is a kinetically controlled reaction which was accounted for in the stability of the transition state. In this particular case, cyclohexa-1,3-diene acts as the diene maleic anhydride acts as the dienophile. The electronegative -(C=O)-O-(C=O)- fragment on maleic anhydride withdraws electron density from the double bond, making it an electron poor dienophile.

Molecular Orbitals of Endo and Exo Transition State

Figure 18:Orbital interactons in the endo and exo TS

Cyclohexa-1,3-diene and maleic anhydride was modelled using GaussView and optimised to a minimum using Gaussian using the HF/3-21G level of theory. The transition state structure was remodelled to resemble cyclohexa-1,3-diene and then the maleic anhydride fragment was added on as the former part of the molecule has already been optimised. The molecular orbitals were visualised and plotted as below (Log 27 and Log 28).

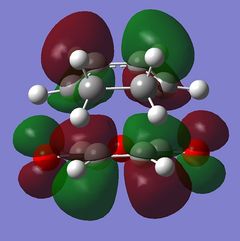
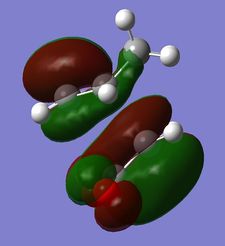
The nodal plane between the -(C=O)-O-(C=O)- fragment and the rest of the molecule indicates that there is no electron density in that area. This suggests that there is no bond formation in the that area as there is no electron density. In the endo isomer, it was observed that the -(C=O)-O-(C=O)- fragment of maleic anhydride is orientated in such a way that its orbitals are close to the butadiene orbitals. This provides additional stability due to the secondary orbital overlap between the electron withdrawing groups in the dienophile and the diene as shown on the right. Primary orbital interactions (blue) are present in both isomers as they are the site of σ-bond formation. However, secondary orbital interactions (red) whereby no bonds are formed are only present in the endo isomer due to the relative orientation of the ring. These interactions are not possible in the exo isomer as the C=O fragment is pointing away from the ring as observed in the HOMO. The only intermolecular interaction present in the exo isomer is the overlap at the site of bond formation. Therefore, in can be concluded that the secondary orbital overlap interaction results in the formation of the kinetic product in the reaction.

Molecular Orbitals of Endo and Exo Transition State
	Exo TS		Endo TS
Reactant	HOMO	LUMO	HOMO	LUMO
Front View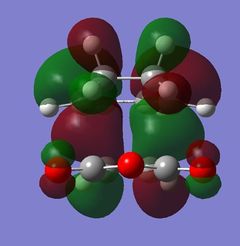
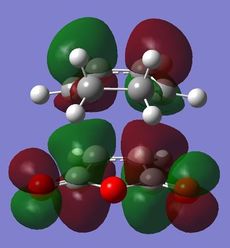
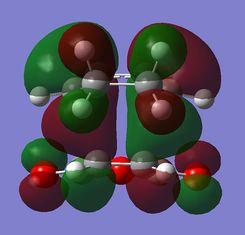
Side View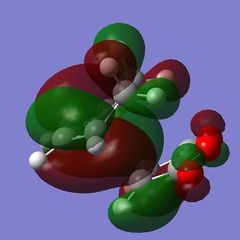

Bond Lengths Analysis

The bond lengths were tabulated from the transition structure modelled using HF/3-21G level of theory. The geometries of both structures were similar with the exception of the through-space interaction of the -(C=O)-O-(C=O)- fragment to specific carbons.

This is particularly interesting as the endo transition state is more strained as observed by the shorter through space distance of the -(C=O)-O-(C=O)- fragment to the -CH=CH- fragment (avg. C2/C3-O10 = 3.09975Å) as compared to the distance with the bridgehead carbons in the exo isomer. (avg C5/C6-O10 = 3.15381Å). A closer distance of 0.05406Å indicates that the endo isomer is subjected to higher steric repulsion. However, the reported dominant product is the more sterically congested isomer which further confirms that the endo isomer is the kinetic product. This stability is attributed to the secondary orbital overlap discussed in the previous section.

Discrepancy between calculated bond lengths and typical C-C and C=C bond lengths were as addressed in the part above (shorter C2-C3 bonds). The intermolecular distance was yet again less than twice the Van der Waals radius which indicates that it is the site of bond formation.

Bond lengths of transition state / Å
Bonds	Exo TS	Endo TS
Intramolecular bond
C1-C2	1.37002	1.37077
C2-C3	1.39756	1.39614
C3-C4	1.37003	1.37080
C5-C6	1.55883	1.56017
C7-C8	1.37312	1.37022
Intermolecular bond
C1-C7	2.26083	2.23124
C4-C8	2.26066	2.23051
Through space interactions
C5-O10 (bridge C)	3.18854	4.53435
C6-O10 (bridge C)	3.18908	4.53465
C2-O10 (diene)	4.44713	3.09995
C3-O10 (diene)	4.44693	3.09955

Thermodynamic Analysis of the Transition States

The vibrational spectrum included a negative frequency, dubbed as the imaginary frequency as discussed in previous sections. This proves that the structure obtained is indeed a transition structure. The vibration was animated and corresponded to the reaction coordinate as seen below. An Intrinsic Reaction Coordinate analysis was performed on both structures using the HF/3-21G level of theory and the results were plotted below (Log 29 and Log 30).

Summary of Endo and Exo TS
	Exo TS	Endo TS
Imaginary Frequency / cm-1	-647.45	-643.84
Imaginary Frequency Animation

Transition state data
	Exo TS	Endo TS
Electronic Energy / Hartree	-605.603591	-605.610368
IRC Spectrum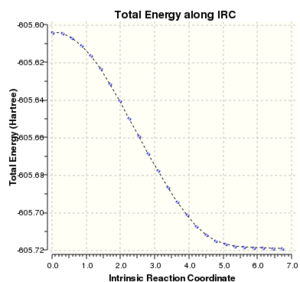
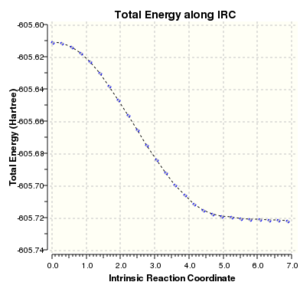
IRC Animation

From the thermochemistry data and also observable from the y-intercept of the IRC spectrum, the endo transition state has a lower electronic energy (endo has a more negative electronic energy). This complements the reported data that the endo isomer is the kinetic product. Reaction following the exo transition state forms a more energetically stable product as observed by the steeper gradient and the lower plateau value, further proving that it is the thermodynamic product.

Further Discussion

In the calculations above, solvent effects were negated. The endo isomer is the predominant product at 298.15 K but the reaction pathway could be altered with a change in solvent or temperature in which calculations have to be re-performed. For simplicity purposes, the solvent settings have been set to Default in the Gaussian solvent option as we are primarily discussing the stability of the transition states.