Rep:Mod:yh3511

Computational Physical Chemistry

In this set of computational experiments, the transition structures of the Cope rearrangement and Diels-Alder cycloadditions are analysed using Gaussian. Bond lengths and corresponding energies of each transition state are calculated. These information are used to understand the reaction path of the reaction.

The Cope Rearrangement

1,5-hexadiene, optimized using HF/3-21G

1,5-hexadiene, optimized using HF/3-21G

	Energy/Hartrees	Point group	Image
Anti 1	-231.69260236	C2
Anti 2	-231.69253530	Ci
Anti 4	-231.696097055	C1
Gauche 1	-231.68771615	C2
Gauche 4	-231.69153036	C2

Comparing a.p.p confirmations with gauche ones, it is observed that generally gauche structures have a lower energy than a.p.p ones. Therefore the lowest energy confirmation of 1,5-hexadiene may be one of the gauche confirmations (Gauche 1).

1,5-hexadiene (anti 2), optimized using B3LYP/6-31G*
Energy: -234.61171035 ( Energy is significantly smaller compared to the one run by HF/3-21G)
The structure looks similar with the one calculated before.

Anti 2 DFT

Sum of electronic and zero point energies: -234.469204
Sum of electronic and thermal energies: -234.461857
Sum of electronic and thermal enthalpies: -234.460913
Sum of electronic and thermal free energies: -234.50077


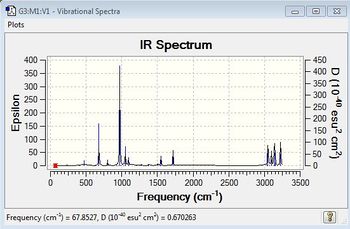
1,5-hexadiene (anti 2), optimized frequency
No negative frequency observed.

Optimization of the "Chair" and "Boat" Transition Structures

Optimized CH₂CHCH₂ using HF/3-21G

By copying the image into a new Gaussian window and setting the distance between the two terminal carbons as 2.2Å, a guess strucure of the chair is generated.

Hartree Fock and the default basis set 3-21G is used for the following parts in this section.

Chair and boat transition states calculated by different methods

		Image	New bond distance/Å	Electronic Energy /hartree
Chair	TS Berny		2.021 and 2.020	-231.61932243
	Redundant Coordinate Editor		2.020 and 2.021	-231.61932237
	Intrinsic Reaction Coordinate (IRC)		1.55249 and 4.23169	-231.69166702
	B3LYP/6-31G*		1.96755 and 1.96755	-234.55698303
Boat
	B3LYP/6-31G*		2.20663 and 2.20663	-234.54309307
	QST2 (failed boat)		3.07636 and 3.07636	-231.62900948
	QST2 (successful boat)		2.13978 and 2.14050	-231.60280161

Chair structure

IR spectrum from TS Berny (no imaginary frequency)

Boat structure
Animation

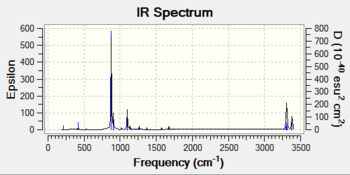
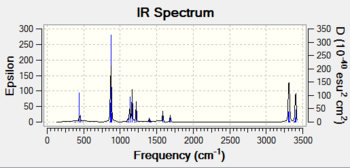
IR spectrum (one negative frequency at 840.00 cm^-1)

Summary of energies (in hartree)

B3LYP/6-31G*

	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
Boat TS	-234.54309307	-234.402342	-234.3960006
Chair	-234.55698303	-234.414929	-234.409009
Anti 2	-234.61171035	-234.469204	-234.461857

Summary of energies (in hartree)

HF-3-21G

	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
Boat TS	-231.60280161	-231.450927	-231.445298
Chair	-231.61932237	-231.466700	-231.461341
Anti 2	-231.692538	-231.539535	-231.532564

Summary of activation energies(in kcal/mol)

	B3LYP/6-31G*		HF-3-21G
	at 0 K	at 298.15 K	at 0 K	at 298 K
Boat	41.96	41.33	55.60	54.76
Chair	34.06	33.16	45.70	44.69

The Diels Alder Cycloaddition

AM1 semi-empirical molecular orbital method was used for the following calculations.
i) cis butadiene

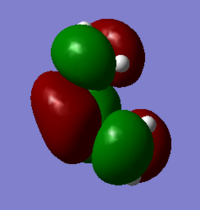
HOMO
Antisymmetric

LUMO
Symmetric

ii)Transition State geometry
QTS2 method was used

Transition state

New bond length:2.11956Å and 2.11857Å
Energy: 0.112a.u.
Lowest positive frequency:147.19cm^-1

HOMO

Antisymmetric

LUMO

Symmetric

The animation of the transition state

The animation of the lowest frequency

Discussion
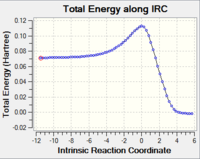
Typical sp³ bond length is 1.54 Å and typical sp₂ bond length is 1.34 Å. The van der Waals radius of the C atom is 1.7Å. The newly formed C-C bonds are longer than typical sp² and sp³ c-c bonds, but shorter than two vdW radius of carbon atoms. This suggests there are some interaction between the two carbons, but the distance is not close enough to form a bond. This is the evidence of a transition state structure. Also the two new C-C bonds are about the same in length, which means bond formation is synchronous. This is confirmed by the vibration at the imaginary frequency. The vibration of the lowest positive frequency however only represents the vibration of the molecule instead of the transition state.

For the symmetric LUMO, from the MO diagram it is clear that there are no overlap between the ethylene and butadiene orbitals. The overlap only exits in the antisymmetric HOMO. Therefore the HOMO from butadiene and the LUMO from ethene are used to form this transition state antisymmetric MO. This reaction is symmetry allowed.

iii)Diels Alder Reaction
Endo transition state

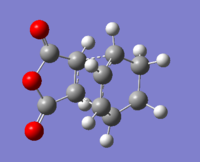
Energy: -0.05150464 a.u. Sum of electronic and zero-point Energies=0.133494 a.u. Sum of electronic and thermal Energies=0.143683 a.u.
New bond length:2.1616Å and 2.1628Å (longer than normal C-C bonds
C-C through space distances between the -(C=O)-O-(C=O)- fragment: 2.2792Å for both
C-C through space distances between C atoms of the “opposite” -CH=CH: 2.8912Å and 2.8905Å
C-C bondg lengths are shorter in the maleic anhydride ring than in the Cyclohexa-1,3-diene ring

HOMO

Antisymmetric

Exo transition state

Energy: -0.05041976 a.u. Sum of electronic and zero-point Energies=0.134881 a.u. Sum of electronic and thermal Energies=0.144882 a.u.
New bond length:2.171Å and 2.170Å (longer than normal C-C bonds)
C-C through space distances between the -(C=O)-O-(C=O)- fragment: 2.2796Å
C-C through space distances between C atoms of the “opposite” -CH=CH: 2.9451Å and 2.9450Å
C-C bond lengths are shorter in the maleic anhydride ring than in the Cyclohexa-1,3-diene ring, the same as endo

HOMO

Antisymmetric

Discussion
In the structure of the endo form, there is a favourable overlap between the π orbitals on the maleic anhydride and the diene HOMO. The exo product can be considered to be more strained in this sense. However from the through space C-C distances it is observed that the exo form has less steric strains (longer through space distances). In this case, the endo form is the predominate product as it has a lower transition state energy, which means the secondary orbital overlap effect dominates in this case.

Further analysis on the endo and exo forms using B3LYP/6-31G*
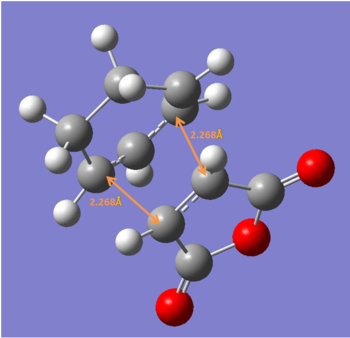
Endo

test molecule

Exo

test molecule

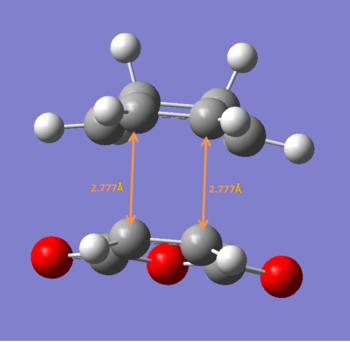
After reoptimization using B3LYP/6-31G*, the newly formed C-C bond is more consistent with synchronous bond formation.

Further Discussion

Diels−Alder cycloaddition of 4-Chloro-2(H)-pyran-2-one with methyl acrylate

i)Four substituted bicyclic lactone cycloadducts (5-endo, 6-endo, 5-exo, 5-endo) are analysed using QST2 method with AM1 semi-empirical molecular orbital method

endo 5.

endo 6.

exo 5.

exo 6.

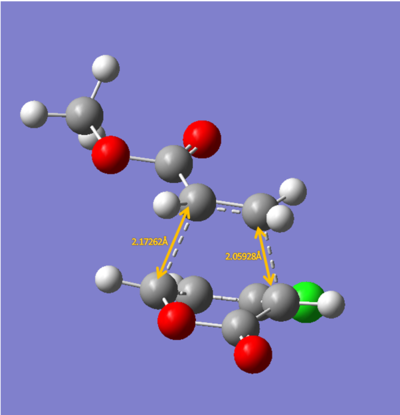
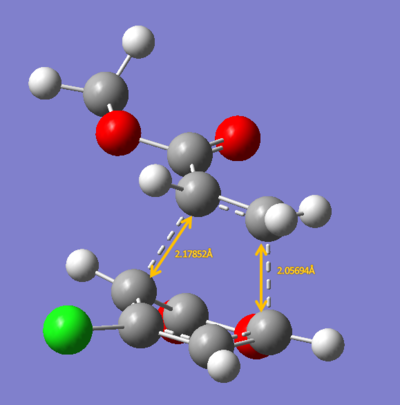
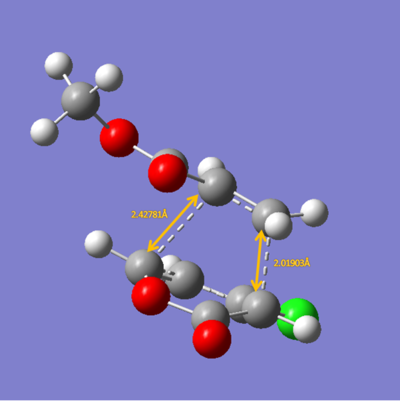
The energies calculated were shown in the table below

Energies of different adducts

	Endo 5	Endo 6	Exo 5	Exo 6
Energy/ a.u.	-0.1440	-0.1476	-0.1410	-0.1413

The exo-5 form has the highest energy and the endo-6 form has the lowest energy.
The bond lengths calculated are quite different from the ones reported in the paper ,therefore further calculation were carried out using DFT method (B3LYP/6-31G*).

ii) The four transition states were reoptimized using DFT method (B3LYP/6-31G*).

endo 5.

endo 6.

exo 5.

exo 6.

Energies of different adducts

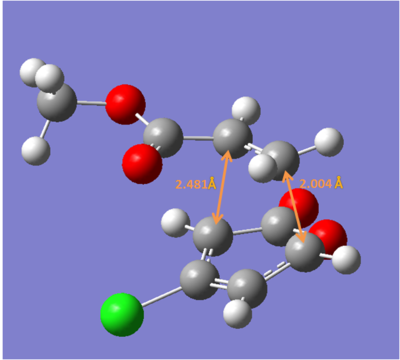
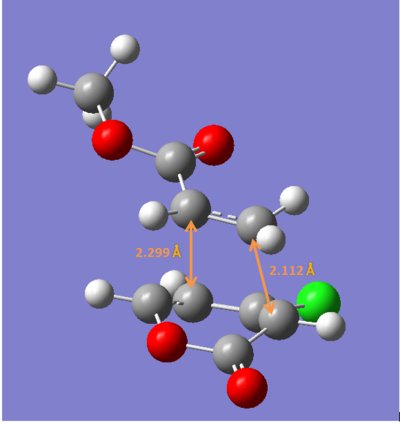
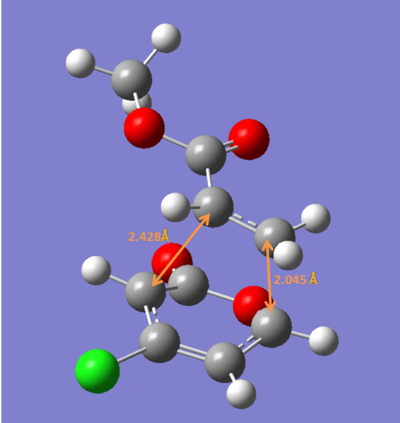
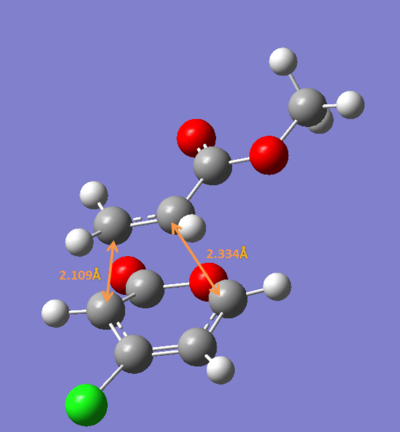
	Endo 5	Endo 6	Exo 5	Exo 6
Energy/ a.u.	-1109.3930	-1109.3941	-1109.3902	-1109.3910

The exo-5 form has the highest energy and the endo-6 form has the lowest enenrgy.
Concluding from the energies above, the endo-6 form would have the highest yield while the exo-6 form would have the lowest yiled. This consists with the experimental results.