Rep:Mod:yh1710

Optimisation of a Molecule

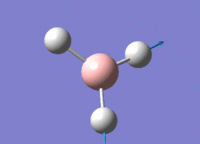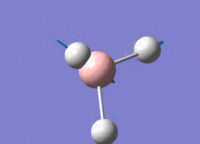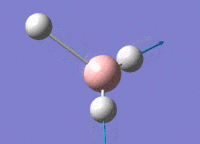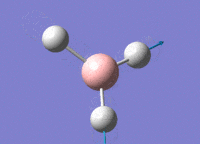
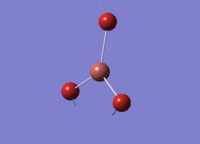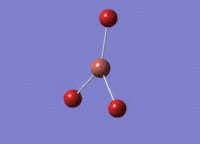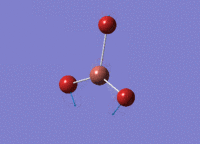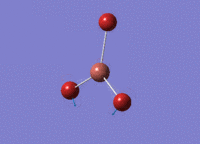
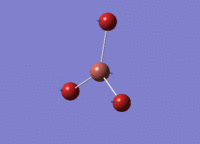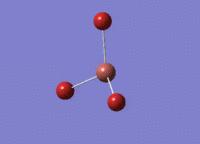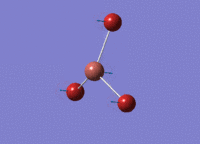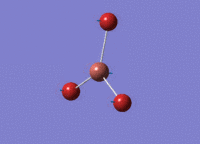
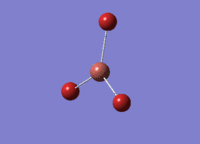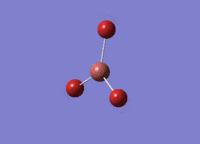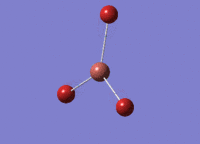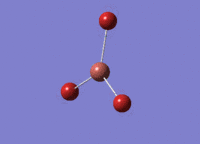
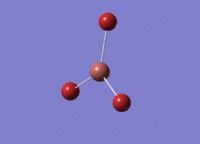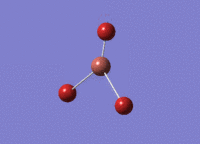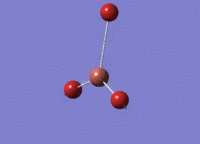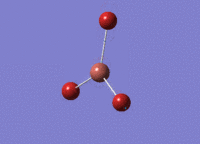
BH3 - B3LYP, 3-21G optimisation

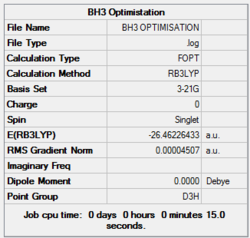
Initially, a minimal basis set (3-21G) was chosen along with a DFT method and B3LYP hybrid functional. Results from log file and Gaussview summary provided below:

Figure 1 - BH₃ Optimisation Summary

Item Table

        Item               Value     Threshold  Converged?
 Maximum Force            0.000413     0.000450     YES
 RMS     Force            0.000271     0.000300     YES
 Maximum Displacement     0.001610     0.001800     YES
 RMS     Displacement     0.001054     0.001200     YES
 Predicted change in Energy=-1.071764D-06
 

Data indicates that the optimisation has been completed where all values have successfully converged – the value for “RMS Gradient Norm” is less than 0.001.

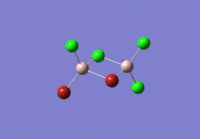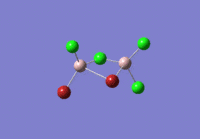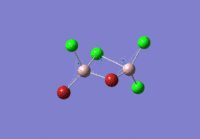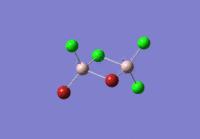
B-H bond distance: 1.19 Å

H-B-H bond angle: 120.0˚ (D₃ symmetry group, trigonal planar)

These values agree with those quoted in literature: 1.19 Å and 120˚ respectively

BH3 - B3LYP, 6-31G d,p optimisation

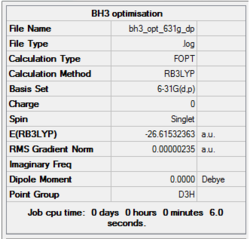
To investigate different parameters of optimisation, a higher level basis set (6-31G d,p) was used in conjunction with the DFT and B3LYP method from the previous calculation.

Results from the log file were saved, and the Gaussview summary is presented below:

Figure 2 - BH₃6-31G d,p Optimisation Summary

Item Table

Item               Value     Threshold  Converged?
 Maximum Force            0.000005     0.000450     YES
 RMS     Force            0.000003     0.000300     YES
 Maximum Displacement     0.000019     0.001800     YES
 RMS     Displacement     0.000012     0.001200     YES
 Predicted change in Energy=-1.304899D-10

The data indicates that the forces and placements have converged suggesting the completion of the optimization - the value for “RMS Gradient Norm” is less than 0.001.

From this point forward, the completion of the optimisation/calculation will not be commented on, but the convergence table should be used as an indicator for this.

B-H bond distance: 1.19 Å

H-B-H bond angle: 120.0˚ (D3 symmetry group, trigonal planar)

Comparison of two optimisation methods

Total energy of 3-21G optimised BH₃: -26.46226433 a.u.

Total energy of 6-31G (d,p) optimised BH₃: -26.61532363 a.u.

TlBr₃ - optimisations using pseudo-potentials (LanL2DZ)

Most of chemistry is based on the assumption that it is really the valence electrons that dominate in bonding interactions, and so we can safely model the core electrons of an atom by a special function called a pseudo-potential (PP). The pseudo-potential is useful in the case where the atoms are large, making these assumptions will save time in calculations (well documented that PP is accurate and does not affect the results significantly for heavy atoms.

Thus an optimisation using PP was performed on TlBr₃ with a point group restriction (D_3h 0.001 - very tight) with the LANL2DZ basis set and B3LYP hybrid functional. The calculation was submitted to the HPC server instead of Gaussian.

The log file was saved and the summary of the optimisation is presented below:

Figure 3 - TlBr₃ Optimisation Summary

Item Table

Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000022     0.001800     YES
 RMS     Displacement     0.000014     0.001200     YES
 Predicted change in Energy=-6.084011D-11

Tl-Br bond distance: 2.65 Å

Br-Tl-Br bond angle: 120.0 (D₃ symmetry group, trigonal planar)

These values agree with those quoted in literature: 2.52 Å and 120 respectively

The optimisation was published onto D-Space which the following link will be directed to: DOI:10042/23335

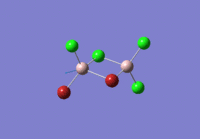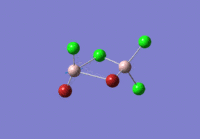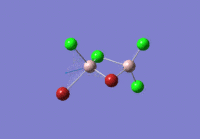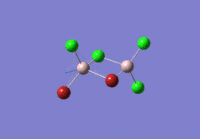
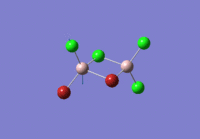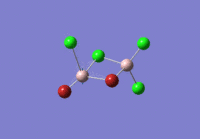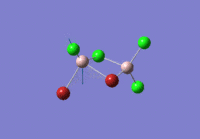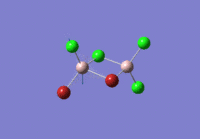
BBr₃ - optimisation using a mixture of basis sets and pseudo potentials

When compunds contain both heavy atoms which require a pseudo-potential, and light atoms, which are treated more accurately with a full basis set we need to be able to mix pseudo-potentials and basis sets. Thus for the optimisation of BBr₃, this very mix of PPs and full basis sets was accounted for.

The calculation was performed with the method set to GEN which allows the option to specify basis sets for each individual atom, and thus an additional keyword ("pseudo=gfinput")was inserted and the following was added to the text file before submission of calculation to HPC:

B 0
6-31G(d,p)
****
Br 0
LanL2DZ
****

Br 0
LanL2DZ

The log file was saved and the summary received from Gaussian is presented below:

Figure 4 - BBr₃ Optimisation Summary

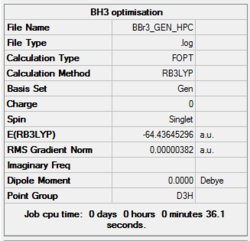
Item Table

Item               Value     Threshold  Converged?
 Maximum Force            0.000008     0.000450     YES
 RMS     Force            0.000005     0.000300     YES
 Maximum Displacement     0.000036     0.001800     YES
 RMS     Displacement     0.000023     0.001200     YES
 Predicted change in Energy=-4.026910D-10

The published file to D-Space is given in the following link: DOI:10042/23336

Comparison of bond distances

Having carried out a series of calculations and optimizations, it is worth comparing the results obtained, particularly the bond lengths as it is the value with the largest degree of variance (understandably). The following table lists the bond length of the three molecules that were investigated:

Table 1 - Comparison of bond lengths

Molecule	Bond Lengths, Å
BH3	1.19
BBr3	1.93
TlBr3	2.65

By comparing the differences in bond length, some conclusions can be drawn regarding the effect of the substituents on the bond length.

A key difference between the substituents Br and H, is their size. As a relatively large atom, the valence orbital in bromine (4p) will be large and very diffuse, which hinders the effectiveness of its electronic interaction (poor overlap) with the boron atom. Another difference worth considering is electronegativity. Bromine has a Pauling electronegativity of 2.74 compared to 2.1 for hydrogen. A value of 2.01 for the boron atom suggest that in terms of electronegativity B and H are a lot more well-matched and results in a higher stabilisation energy and thus shorter bond length.

The same analysis can be conducted for TlBr₃ and BBr₃, in this case determining the effect of changing the central atom on the bond length The same argument as above can be used where Thallium, with its valence 6p orbitals is a lot larger in terms of electronic size in comparison to boron and will be very diffuse with a low electron density. This, as expected, results in a very poor orbital overlap between Tl and Br thus explaining the long bond distance of Tl-Br compared to B-Br.

Bonding in Gaussview

A bond represents the attractive interaction between two or more atoms. It is not necessarily simple force but a combined effect. For example, a bond strength can be affected by the repulsion of nuclei or the attraction between the oppositely charged ions. Thus in some specific cases, Gaussview may not display bonds where they are expected to be. This is a result of the fact that Gaussview is primarily accustomed to bond lengths in organic molecules. Thus when a calculated bond length is longer than that would be usually expected, a bond is not drawn. However, it does not mean that there is no interaction between the atoms, just too weak to be considered as a significant bond.

Frequency Analysis

When we carry out a frequency or vibrational analysis we are doing two things at once. The frequency analysis is essentially the second derivative of the potential energy surface, if the frequencies are all positive then we have a minimum, if one of them is negative we have a transition state. The frequency analysis has another important role to play because it provides the IR and Raman modes to compare with experiment.Thus in this section we will explore the frequency analysis of different molecules to determine their individual IR modes.

BH₃ vibrational analysis

The first molecule we will investigate is BH₃ again due to its simplicity and size. Thus the frequency analysis of BH₃ was performed with the method employed in the previous optimisation of the molecule (DFT, B3LYP, 6-31G (d,p)).

The frequency analysis was performed successfully, and the summary obtained from Gaussian is presented below. It is worth noting that the energy that was calculated is the same value as the previous optimisation calculation, suggesting that the same structure was indeed obtained.

Figure 4 - BH₃ Frequency Analysis Summary

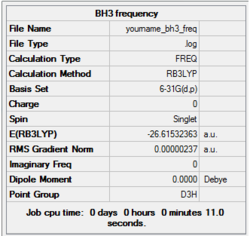
Item Table

Item               Value     Threshold  Converged?
 Maximum Force            0.000005     0.000450     YES
 RMS     Force            0.000002     0.000300     YES
 Maximum Displacement     0.000019     0.001800     YES
 RMS     Displacement     0.000009     0.001200     YES
 Predicted change in Energy=-1.323374D-10

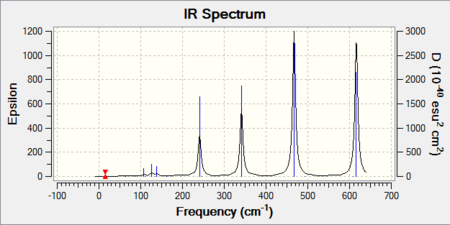
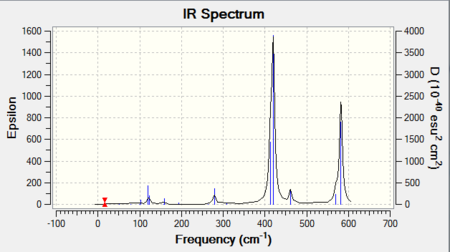
 Low frequencies ---   -0.9033   -0.7343   -0.0054    6.7375   12.2491   12.2824
 Low frequencies --- 1163.0003 1213.1853 1213.1880

The six vibrational modes (3N-6) are indicated in the "Low frequencies". The better the method employed, the closer to zero the six frequencies will be. However any values smaller than +/- 15 cm^-1 are acceptable, and so the method employed is suitable. The vibrations were animated in GaussView and are presented in the table below along with their frequencies, point group and a brief description of the vibrational mode.

Table 2 - Vibrational Modes of BH₃

Number	Vibrational Mode	Frequency/ cm-1	Intensity/ cm-1	Symmetry Point group	Brief description
1	(Wagging)	1163	93	A2'	All three hydrogen atoms are moving simultaneously in and out of plane resulting in a dipole moment. The vector displacements do not describe the boron atom, but it appears to have a small displacement in the opposite direction to the hydrogens.
2	(Symmetrical Stretching)	1213	14	E'	Scissoring action of 2 B-H bond in the plane of the molecule; remaining B-H bond is stationary and rocked with the boron atom due to the stretching of the 2 B-H bonds
3	(Rocking)	1213	14	E'	Asymmetric rocking involving all 3 B-H bonds in the plane of the molecule
4	(Symmetrical stretching)	2582	0	A1'	Symmetric stretch of 3 B-H bonds in the plane of the molecule, while the boron atom is stationary
5	(Asymmetric stretching)	2715	126	E'	Asymmetric stretching of 2 B-H bonds in opposite directions while the third H atom remains stationary, resulting in a slight stretching of the third B-H bond resulting from 2 other B-H bonds
6	(Symmetric stretching)	2715	126	E'	Symmetric stretching of 2 B-H bonds in a concerted fashion, while the remaining B-H bond stretches out of phase resulting in overall asymmetry

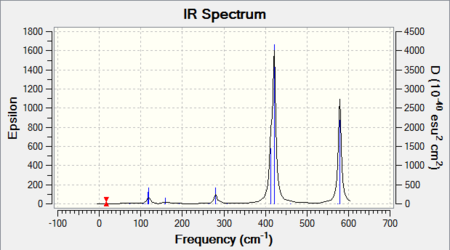
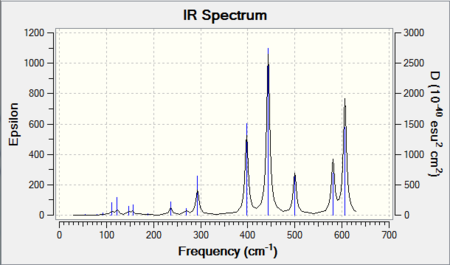
The frequency analysis also yields an infrared spectrum which is presented below in Figure 6. However it can be seen that the spectrum only accounts for three peaks despite there clearly being 6 vibrational modes. There are two reasons for this. Firstly it is because the symmetric stretches are IR inactive as the pre-requisite for IR activity is that vibrations result in a change of dipole. Thus the symmetric A₁' mode is IR silent and does not appear in the spectrum. Secondly the E' vibrations at 1213 cm^-1 and 2715 cm^-1 respectively are degenerate and as seen from the table possess the same frequency. Thus out of the four bands, only two will be present in the spectrum.

Figure 6-Infrared spectrum of BH₃

TlBr₃ vibrational analysis

A frequency analysis of the TlBr₃ was also conducted to confirm that the optimisation of the molecule is at a minimum. The same procedure was applied to the TlBr₃ as the BH₃ but performed using the same method as the optimised structure (DFT, LanL2DZ, 6-31G (d,p)). The GaussView summary is provided below:

Figure 7 - TlBr₃ Frequency Analysis summary

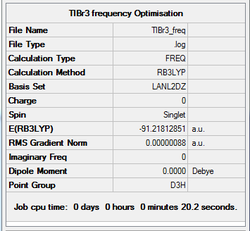
Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000022     0.001800     YES
 RMS     Displacement     0.000011     0.001200     YES
 Predicted change in Energy=-5.660901D-11

The file was submitted to HPC and published to D-Space, which the following link directs to: DOI:10042/23387

Low frequencies ---   -3.4213   -0.0026   -0.0004    0.0015    3.9367    3.9367
 Low frequencies ---   46.4289   46.4292   52.1449

Again the "Low frequencies" were obtained and it can be seen that the analysis method was suitable with frequencies close to zero. Note that the lowest "real" normal mode occurs at 46.4289 cm^-1. The table below presents the vibrational modes (3N-6) along with their respective frequencies, intensities, point groups and a brief description of the vibrational motions.

Table 3 - Frequencies and vibrational modes of TlBr₃

Number	Vibrational Mode	Frequency/ cm-1	Intensity/ cm-1	Symmetry Point group	Brief description
1	(Symmetric scissoring)	46	3.7	E'	Symmetric scissoring motion of 2 Tl-Br bonds in the plane of the molecule
2	(Asymmetric rocking)	46	3.7	E'	Asymmetric rocking of 3 Tl-Br bonds, 2 in one direction, the other in the opposing direction
3	(Wagging)	52	5.8	A2'	Three Br atoms move in/out of plane in a concerted fasion while the central Tl atom moves in the opposite direction
4	(Symmetric stretching)	165	0	A1'	Symmetric stretching of 3 Tl-Br bonds in the plane of the molecule
5	(Asymmetric stretching)	211	25	E'	Asymmetric stretching of 2 Tl-Br bonds in opposite directions while the remaining Tl-Br bond shows a resulting stretching motion from the 2 other Tl-Br motions.
6	(Symmetric stretching)	211	25	E'	Symmetric stretching of 2 Tl-Br bonds concertedly, while the remaining Tl-Br bond stretches in the opposite direction, resulting in an overall asymmetry

IR spectrum presented below:

Figure 8 - TlBr₃ Infrared Spectrum

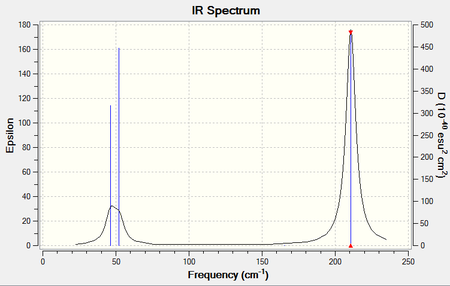
A summary of the vibrational frequencies considered is presented in the table below:

Table 4 - Comparison of vibrational frequencies of TlBr₃ and BH₃

TlBr3 frequency / cm-1	BH3 frequency / cm-1
46	1163
46	1213
52	1213
165	2582
211	2715
211	2715

Numerically, the frequency values of BH₃ are significantly larger than that of TlBr₃. This can easily be rationalised as the vibrational frequency of bonds directly relate to their bond strength, and as discussed earlier the Tl-Br bond strength is much weaker than the B-Br which supports the calculations obtained.

The order of vibrational modes in the two molecules is also slightly different. In BH₃, the order is A2’, E', E', A1', E', E', whereas in TlBr₃, it is E',E', A2’, A1' E', E'. Both however exhibit six modes, consistent with the isostructural relationship of the two molecules. Similarly, in the spectra of the two molecules, both present three vibrational peaks.

A trend that can be seen is the closeness of two different sets of modes, the A2’ and E’ modes and the A1’ and E’ modes. This is perhaps a sign of vibronic coupling between modes of vibration in both molecules. A prerequisite for strong coupling interactions in polyatomic systems is that the two vibrational modes that couple should possess a common atom or bond. In the trigonal planar arrangement, this is easily fulfilled – hence the closeness of the pairs of modes. Thus, modes at higher energy may be a result of coupling interactions experienced by the pair at lower energy.

The same methods and basis sets must be used despite two separate molecules being analysed. This is because using the same methods and basis sets will apply the same parameters and the same approximations (this includes errors as well). This way even if there are some weaknesses in the calculations, the limitations/errors will be the same for both molecules, so comparison is more reliable and valid. Different methods and basis sets would mean that the calculation would be done differently, with different level of accuracy and the error. Hence, it is important to ensure that all the analysis are made based on same set-up, to ensure that the answers would have similar level of accuracy and the error would be similar.

A frequency analysis enables us to ensure that the optimisation was done correctly. For the optimisation to be successful, it has to be either a highest point/peak or a lowest point/trough. This is carried out by taking the first and second derivatives. At any stationary point, the first derivative should be close to 0. The frequency analysis test the second derivative. If all second derivative are positive, a minimum is obtained. If one negative value is obtained, then a maximum is obtained. Thus by checking with frequency analysis, one can ensure that the calculation was done correctly.

Population analysis

Molecular orbitals of BH₃

One of the very useful aspects of carrying out calculations is that the electronic structure is solved and we obtain the MOs. These are the quantitative or computed MOs which we can compare to the qualitative or approximate MOs produced via MO diagrams. By selecting "Energy" as the method, typing in the additional keyword "pop=full" and selecting "Full NBO" the MO analysis is switched on, and depiction of the molecular orbitals of BH₃ can be obtained.

The energy calculation was performed using the previously optimised structure (DFT, B3LYP, 6-31G (d,p)) and the log file was obtained and saved. In addition the GaussView summary is provided in the image below:

The file was submitted to HPC and the published in D-Space (DOI:10042/23386 )

The MO diagram constructed using the LCAO method is presented in Figure 10. Computed visualisations of the MOs are also included alongside the theoretical model. It can be seen from Figure 10 that there are no significant differences between the "real" MOs and the LCAO MOs, thus validating qualitative MO theory as an accurate tool in modelling the molecular framework of simple molecules.

Figure 10 - MO diagram of BH₃ including both the real and LCAO orbitals

NBO analysis

In quantum chemistry, a natural bond orbital or NBO is a calculated bonding orbital with maximum electron density. NBO methodology is based intrinsically on the quantum wavefunction W and its practical evaluation by modern computational methods. Unlike conventional valence bond (VB) or molecular orbital (MO)viewpoints, NBO theory makes no assumptions about the mathematical form of W. Instead, the NBO bonding picture is derived from variational, perturbative, or density functional theoretic (DFT) approximations of arbitrary form and accuracy, up to and including the exact W.

NH₃ optimisation practice

To implement the concept of NBO in computational chemistry, the NBO analysis was performed on NH₃. The same basis set was used as for the higher level BH₃ calculation (DFT, B3LYP, 6-31G (d,p)). Because this molecule is so small we can in-fact go straight to the high level basis set. The additional keyword "nosymm" was added.

The log file of the optimisation was saved, and the GaussView summary of the optimisation is provided below:

Figure 11 - NH₃ 6-31G (d,p) Optimisation Summary

Item               Value     Threshold  Converged?
 Maximum Force            0.000024     0.000450     YES
 RMS     Force            0.000012     0.000300     YES
 Maximum Displacement     0.000079     0.001800     YES
 RMS     Displacement     0.000053     0.001200     YES
 Predicted change in Energy=-1.629727D-09

Frequency analysis

Having successfully performed an optimisation of the NH₃ (where all forces have converged) the frequency analysis was conducted to ensure a minimum was obtained.

The log file was saved and the GaussView summary is presented below:

Figure 12 - Frequency Analysis of NH₃

Item               Value     Threshold  Converged?
 Maximum Force            0.000022     0.000450     YES
 RMS     Force            0.000009     0.000300     YES
 Maximum Displacement     0.000078     0.001800     YES
 RMS     Displacement     0.000039     0.001200     YES
 Predicted change in Energy=-1.621683D-09

Low frequencies ---  -30.7013   -0.0011    0.0008    0.0012   20.2662   28.2997
 Low frequencies --- 1089.5562 1694.1246 1694.1863

The minimum was obtained and the low frequencies are presented above. Note that two of the frequencies exceed 15cm^-1. Although this is not ideal, the deviation was determined to be acceptable for further calculations.

Population analysis

The energy calculation was performed using the previously optimised structure (DFT, B3LYP, 6-31G (d,p)), in order to obtain the NBOs in the next section.

The log file was saved and the GaussView summary is provided below:

Figure 13 - Energy summary of NH₃

NBO analysis of NH₃

Now we are going to carry out a "Natural Bond Orbital Analysis", both inside Gaussview and in the log file from Gaussian.Initially the NBO was visualised where the atoms were coloured by charge.

The charge range is between -1.000 and 1.000

Figure 14 - NH₃ NBO Analysis (Charge coloured atoms)

Figure 15 - NH₃ NBO Analysis (Window summary of NBO manipulation)

Figure 16 - NH₃ NBO Analysis (Charge numbered atoms)

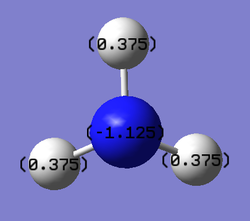
NBO charge on nitrogen: -1.125

NBO charge on hydrogen: 0.375

The NBO analysis gives much more information than the "atomic charges", however GaussView only provides a graphical interface for viewing specific information, it is not sophisticated enough to deal with the NBO analysis. Thus to extract crucial information in NBO analysis one must look in the log file and thus obtain information regarding bond orbital/coefficents/hybrids, the Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis and most importantly, a summary of the natural bond orbitals (energy and population or occupation of the N-H bonds, and the nitrogen lone pair)

NH₃BH₃ Analysis

Ammonia borane NH₃BH₃ is an interesting compound worth investigating. Its high hydrogen content which may allow it to serve as an alternative for hydrogen storage as it is a stable solid at r.t. eliminating the need for high pressure storage tanks. More importantly in the case of this project, it is an acid-base complex and thus determining the energy between the N-B bond may shed light on the dative bonding seen in Lewis acid-base pairs.

To compute a reaction energy, which in this case is the dative bond energy, we need the energy of the reactants and products.As we have already performed calculations on the two reactants, we will focus on completing calculations on the product.

3-21g optimisation

Initially, a minimal basis set (3-21G) was chosen along with a DFT method and B3LYP hybrid functional.

The log file was saved and the Gaussview summary is provided below:

Figure 16 - NH₃BH₃ 3-21G Optimisation summary

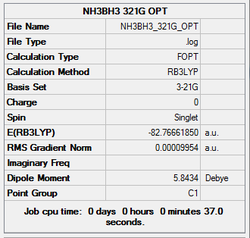
Item               Value     Threshold  Converged?
 Maximum Force            0.000185     0.000450     YES
 RMS     Force            0.000075     0.000300     YES
 Maximum Displacement     0.001140     0.001800     YES
 RMS     Displacement     0.000344     0.001200     YES
 Predicted change in Energy=-3.375293D-07

6-31g (d,p) optimisation

Next, a higher level basis set (6-31G, (d,p)) was chosen along with a DFT method and B3LYP hybrid functional.

The log file was saved and the Gaussview summary is provided below:

Figure 17 - NH₃BH₃ 6-31G (d,p) Optimisation summary

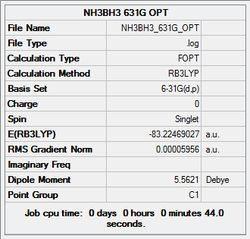
Item               Value     Threshold  Converged?
 Maximum Force            0.000143     0.000450     YES
 RMS     Force            0.000038     0.000300     YES
 Maximum Displacement     0.001016     0.001800     YES
 RMS     Displacement     0.000222     0.001200     YES
 Predicted change in Energy=-1.148584D-07

Frequency analysis

A further frequency analysis was performed using the previously optimised structure (DFT, B3LYP, 6-31G (d,p))

The log file was saved, and the Gaussview summary is provided below:

Figure 18 - NH₃BH₃ Frequency Analysis summary

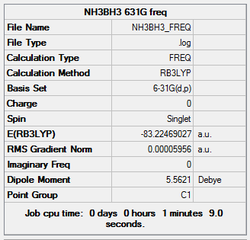
Item               Value     Threshold  Converged?
 Maximum Force            0.000271     0.000450     YES
 RMS     Force            0.000060     0.000300     YES
 Maximum Displacement     0.001492     0.001800     YES
 RMS     Displacement     0.000378     0.001200     YES
 Predicted change in Energy=-2.217937D-07

 Low frequencies ---   -9.2622    0.0007    0.0008    0.0010   19.3386   19.5577
 Low frequencies ---  263.2748  631.1791  638.5342

Determination of the Dissociation Energy

Summary of the energies calculated from optimised structures:

E(NH₃)= -55.55776856a.u.

E(BH₃)= -26.61532374a.u.

E(NH₃BH₃)= -83.22468993 a.u.

Dissociation for NH₃BH₃ adduct is the difference between the energy of a molecule of NH₃BH₃ and the sum of the energies of its components (NH₃ and BH₃). The result was converted from atomic units (a.u.) to kJ/mol via the conversion ratio of 2625.50.

E_dissociation = E(NH₃BH₃) - E(NH₃ + BH₃)

E_dissociation = (-83.22468993)-[(-56.55776856)+(-26.61532374)] = -0.05159763 a.u.

E_dissociation = -135.4 kJ/mol

Mini-Project - Lewis Acids and Bases

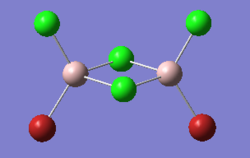
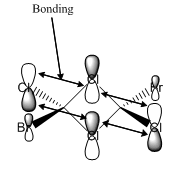
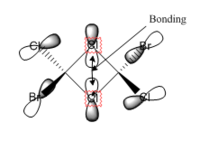
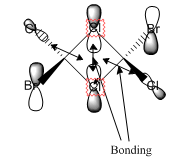
AlClBr₂ is a strong Lewis acid. However it shows a strong tendency to aggregate and form dimers (Al₂Cl₂Br₄) as it is common for heavier main group halides to exist as aggregates larger than implied by their empirical formulae. The halide bridge in the dimer can either be formed via the Cl atoms or Br atoms, and this yields interesting observations in terms of characterisation. In this section we will investigate the different isomers (conformers) of Al₂Cl₂Br₄ as well as their vibrations and MOs.

Conformers of Al₂Cl₂Br₄

The dimer molecule Al₂Cl₂Br₄ can take 4 possible isomers with different symmetries. This section will focus on optimising the four isomers and comparing their energies relative to each other to determine the lowest energy conformer.

Optimisation and Frequency Calculations

As the dimer contains both light and heavy atoms, it is necessary to combine full basis set and pseudo-potential calculations. Thus all optimisation and frequency calculations were carried out using B3LYP functional and 6-31G (d,p) basis set for Al and Cl atoms (light), and LANL2DZ pseudo-potential was used for Br atoms. This was done by selecting "GEN" as the method and editing the text file to contain the following segment:

Title Card Required

0 1
 B                  0.00000000    0.00000000    0.00000000
 Br                 0.00000000    2.02000000    0.00000000
 Br                 1.74937123   -1.01000016    0.00000000
 Br                -1.74937123   -1.01000016    0.00000000

 1 2 1.0 3 1.0 4 1.0
 2
 3
 4

Al 0
6-31G(d,p)
****
Cl 0
6-31G(d,p)
****
Br 0
LanL2DZ
****

Br 0
LanL2DZ

Due to the size of the molecule, the files were submitted to the HPC for faster calculation. The log file of isomer 1, isomer 2, isomer 3, isomer 4 were saved, and a table of summary of the results from Gaussview are provided below. Furthermore the frequency analysis log files were saved 1,2,3 and 4 and the low frequencies were shown to ensure that the minimum was obtained.

Table 1: Optimisation Summary Cl2Al(μ-Br2)AlCl2 Point Group D2h Energy (au) -2352.40630796 RMS Gradient Norm (au) 0.00000782 Dipole Moment (Debye) 0.0000 Spin Singlet File Name AlBr2Cl4_Optimisation_1_GEN File Type .log Calculation Type FOPT Calculation Method RB3LYP Basis set Gen Item Value Threshold Converged? Maximum Force 0.000029 0.000450 YES RMS Force 0.000011 0.000300 YES Maximum Displacement 0.000684 0.001800 YES RMS Displacement 0.000283 0.001200 YES Predicted change in Energy=-1.429895D-08 Optimization completed. Low frequencies --- -5.1291 -5.0818 -3.1866 -0.0035 -0.0029 -0.0028 Low frequencies --- 14.8601 63.2605 86.0507 Table 2: Optimisation Summary ClBrAl(μ-Cl2)AlClBr Point Group C2v Energy (au) -2352.41626666 RMS Gradient Norm (au) 0.00002825 Dipole Moment (Debye) 0.1655 Spin Singlet File Name AlBr2Cl4_Optimisation_2_GEN File Type .log Calculation Type FOPT Calculation Method RB3LYP Basis set Gen Item Value Threshold Converged? Maximum Force 0.000085 0.000450 YES RMS Force 0.000033 0.000300 YES Maximum Displacement 0.001780 0.001800 YES RMS Displacement 0.000644 0.001200 YES Predicted change in Energy=-1.198828D-07 Optimization completed. Low frequencies --- -3.5628 -2.3451 -0.0037 -0.0029 0.0004 1.1905 Low frequencies --- 17.1982 50.9748 78.5446 Table 3: Optimisation Summary Trans-BrClAl(μ-Cl2)AlClBr Point Group C2h Energy (au) -2352.41628781 RMS Gradient Norm (au) 0.00001766 Dipole Moment (Debye) 0.0059 Spin Singlet File Name AlBr2Cl4_Optimisation_3_GEN File Type .log Calculation Type FOPT Calculation Method RB3LYP Basis set Gen Item Value Threshold Converged? Maximum Force 0.000043 0.000450 YES RMS Force 0.000016 0.000300 YES Maximum Displacement 0.000643 0.001800 YES RMS Displacement 0.000177 0.001200 YES Predicted change in Energy=-2.765048D-08 Optimization completed. Low frequencies --- -4.1561 -2.2615 -0.0023 0.0014 0.0018 0.9283 Low frequencies --- 17.6821 48.9672 72.9470 Table 4: Optimisation Summary BrClAl(μ-Br,Cl)AlCl2 Point Group C1 Energy (au) -2352.41109945 RMS Gradient Norm (au) 0.00001086 Dipole Moment (Debye) 0.1380 Spin Singlet File Name AlBr2Cl4_Optimisation_4_GEN File Type .log Calculation Type FOPT Calculation Method RB3LYP Basis set Gen Item Value Threshold Converged? Maximum Force 0.000017 0.000450 YES RMS Force 0.000009 0.000300 YES Maximum Displacement 0.000307 0.001800 YES RMS Displacement 0.000119 0.001200 YES Predicted change in Energy=-8.565767D-09 Optimization completed. Low frequencies --- -24.1985 -20.9534 -17.4655 -0.0022 -0.0016 -0.0010 Low frequencies --- 7.6726 54.3100 79.8419 Relative Energies The energies of the four different isomers of Al2Br2Cl4 were given in the Gaussview summary, and presented in atomic units (a.u.). These values are very close to one another, and the unit are difficult to relate to. So the energies were converted from a.u. to kJ/mol (conversion ratio:2625.50) and presented as relative energies and tabulated as seen below. Table 5: Relative energies of isomers of Al2Cl4Br2 Isomer Energy (a.u.) Energy (kJ mol-1) Relative Energy (kJ mol-1) Cl2Al(μ-Br2)AlCl2 -2352.40630796 -6176242.762 26.230 Cis-BrClAl(μ-Cl2)AlClBr -2352.41626666 -6176268.908 0.084 Trans-BrClAl(μ-Cl2)AlClBr -2352.41628781 -6176268.992 0.00 BrClAl(μ-Br,Cl)AlCl2 -2352.41628761 -6176255.340 13.652 It can be seen from Table 5 that the lowest energy isomer is isomer 3 (Trans-BrClAl(μ-Cl2)AlClBr. However, as the B3LYP functional is only accurate to 10 kJ/mol, isomer 2 can be considered to be equally low in energy. This is evident as the trans/cis positioning of the Br atoms should not have any impact on the energy of the molecule. Given the accuracy of the calculation method, it is difficult to judge whether isomer is in fact also equally low in energy c.f. isomer 2 and 3. However judging from the molecular structure of the isomer, the major difference in energy of the molecules must result from the difference of the bridging atoms i.e. Br or Cl. The stability of the molecule relies strongly on the extent of bonding between Al and the bridging halides, which in turn relies on the extent of overlap for the Al-X (X=halide) bridging bond. By considering bonding of Cl and Br with Al, the computational calculations can be rationalised. The Al-Cl bond consists of bonding between 3p orbitals where as the Al-Br bond consists of the 3p orbital from Al overlapping with the 4p orbital from Br. The 4p orbital in Br is larger and thus more diffuse than the Cl 3p orbital and thus results in poorer overlap with the Al 3p orbital which ultimately results in a weaker bond, and less stable molecule. The order of energy of the molecule is thus rationalised. An alternative rationalisation of the energy of stability of the isomers is by considering the monomer AlCl2Br as a Lewis acid, which when forming a Lewis adduct will lose the Al-X π contributions as they change from trigonal planar to tetrahedral in shape and lower the stabilisation energy to varying degrees depending on the halide. Thus the order of stability is determined by the difference between the energy associated with the loss of the π contribution and the energy related to the acid base adduct formation. This follows the order Al-F3, Al-Cl3, Al-Br3, and thus rationalises the computed results of isomers with chloride as the bridging halides being lower in energy compared to those with bromide as the bridging halide(s). Dissociation Energy The dissociation energy of the lowest energy conformer into two AlBrCl2 monomers is determined by finding the difference in energy between the Trans-BrClAl(μ-Cl2)AlClBr and two monomers. This is done by optimising the monomer molecule allowing the determination of the energy and applying the following equation: Edissociation = 2Emonomer - Eadduct Table 6: Optimisation Summary of AlBrCl2 AlBrCl2 Point Group C2V Energy (au) -1176.19013696 RMS Gradient Norm (au) 0.00001820 Dipole Moment (Debye) 0.1128 Spin Singlet File Name AlBrCl2_Optimisation_GEN File Type .log Calculation Type FOPT Calculation Method RB3LYP Basis set Gen Item Value Threshold Converged? Maximum Force 0.000037 0.000450 YES RMS Force 0.000018 0.000300 YES Maximum Displacement 0.000339 0.001800 YES RMS Displacement 0.000146 0.001200 YES Predicted change in Energy=-1.284612D-08 Optimization completed. Low frequencies --- -3.2986 -0.2141 0.0013 0.0031 0.0034 2.3016 Low frequencies --- 120.4960 133.8269 185.7160 Having determined the energy of monomer from the optimisation and ensuring the minimum from the frequency analysis, the equation above can be applied to determine the dissociation energy: Edissociation = 2 x (-1176.19013696*2625.50) - (-6176268.992) = 94.58 kJ/mol Thus we have determined the energy of dissociation and from the +ve value of the result, we can conclude that the adduct form is more stable than the two monomers existing individually, where energy is required to separate the dimer into its corresponding monomers. Spectroscopy The IR spectroscopy is worth discussing as the spectrum of each individual isomer will be different due to their respective symmetry components. Thus the IR spectra are presented below and the active vibrations are also tabulated next to their corresponding animation giving a clear illustration of the vibrational mode. Furthermore the symmetry of each isomer will be discussed with respect to the absorption bands (also presented in the table). Cl2Al(μ-Br2)AlCl2 (Isomer 1) Figure 1 - IR spectrum of Cl2Al(μ-Br2)AlCl2 Table 7 - Frequencies and vibrational modes of Cl2Al(μ-Br2)AlCl2 Number Vibrational Mode Frequency/ cm-1 Brief Description 1 241 Concerted motion of Al in the same direction resulting in simultaneous bridging Al-Br stretching and compression, and AlBr2 wagging 2 341 Concerted motion of Al in same direction leading to simultaneous Al-Cl stretching and compression 3 467 Similar to vibrational mode 1 but with Al-Cl stretching rather than wagging 4 616 Similar to vibrational mode 3 but with stronger Al-Cl stretching. Cis-BrClAl(μ-Cl2)AlClBr (Isomer 2) Figure 2 - IR spectrum of Cis-BrClAl(μ-Cl2)AlClBr Table 8 - Frequencies and vibrational modes of Cis-BrClAl(μ-Cl2)AlClBr Number Vibrational Mode Frequency/ cm-1 Brief Description 1 419 Concerted motion of Al in the same direction resulting in simultaneous bridging Al-Cl stretching and compression, and wagging terminal bonds 2 461 Out-of-phase concerted motion of Al atoms, resulting in simultaneous bridging Al-Cl stretching and terminal bonds wagging 3 582 Concerted motion of Al in the same direction resulting terminal bond stretching. Note that the Br atoms and the bridging atoms are almost stationary. Trans-BrClAl(μ-Cl2)AlClBr (Isomer 3) Figure 3 - IR spectrum of Trans-BrClAl(μ-Cl2)AlClBr Table 9 - Frequencies and vibrational modes of Trans-BrClAl(μ-Cl2)AlClBr Number Vibrational Mode Frequency/ cm-1 Brief Description 1 421 Concerted motion of Al in the same direction resulting in simultaneous bridging Al-Cl stretching and compression, and wagging terminal bonds 2 579 Concerted motion of Al in the same direction resulting terminal bond stretching. Note that the Br atoms and the bridging atoms are almost stationary. BrClAl(μ-Br,Cl)AlCl2 (Isomer 4) Figure 4 - IR spectrum of BrClAl(μ-Br,Cl)AlCl2 Table 10 - Frequencies and vibrational modes of BrClAl(μ-Br,Cl)AlCl2 Number Vibrational Mode Frequency/ cm-1 Brief Description 1 291 Bridging Al-Cl bond stretching and wagging motion of terminal AlCl2. Note that all other bonds and atoms are more or less stationary. 2 398 Stretching motion of bridging halides. 3 443 Strong motion from one of Al atoms resulting in terminal and bridging bonds stretching connected to that Al atom. 4 500 Strong motion from other Al atom resulting in terminal and bridging bonds stretching connected to that Al atom. 5 580 Strong motion from one of Al atoms resulting in terminal bond stretching 6 606 Strong motion from other Al atom resulting in terminal bond stretching The key observation that should be noted is the differences between the stretching vibration of terminal Al-Br bonds and bridging Al-Br bonds. For the B2H6 diborane dimer, the briding B-H bond is weaker than the terminal. This is because the two electrons participating in the bonding are spread out over three internuclear spaces thus diffusing the electron density and decreasing the bond order, ultimately decreasing the stretching vibration (119 pm vs. 133 pm). Contrary to the diborane, the opposite trend is observed where the briding Al-X (X=Halide) bond is stronger than the terminal (e.g. Al2cl6: 221 pm vs. 206 pm). This is because the bridging bond involves the lone pairs on the halide (absent in the B-H bridging bond) which in fact allow a total of 4 electrons to participate in the three centre bonding system. This results in an increase in the bond order compared to the bridging Al-X bond, and thus leads to a higher stretching frequency. This is in fact observed from analysing the vibrations of the isomers and comparing the terminal and bridging Br bonds, where analysis of isomer 1 shows that the bridging Al-Br bond stretch is at a higher value than the terminal Al-Br bond stretch in isomer 3. Note that the former is an asymmetric stretch and the later is a symmetric stretch (i.e. not IR active) Table 11: Comparing the vibrations of terminal and bridging Al-Br bonds Cl2Al(μ-Br2)AlCl2 Asymmetric stretch ClBrAl(μ-Cl2)AlClBr Symmetric stretch Briding Al-Br bond: 467 cm-1 Terminal Al-Br bond: 459 cm-1 Molecular Orbitals The molecular orbitals of the occupied non-core MOs (83-60) were visualised by doing the energy calculation using Gaussview. 5 MOs are presented in the table below and analysed in terms of their bonding and anti-bonding characteristics. The five generated MOs were associated with the theoretical molecular orbitals as well as a brief description of the bonding interactions present. Table 12 - MO orbitals generated from Gaussview and the theoretical equivalent MO 77 (-0.33839 a.u) MO 73 (-0.37099 a.u.) MO 67 (-0.41014 a.u.) MO 80 (-0.31760 a.u.) MO 78 (-0.33370 a.u.) The p orbital of all the Cl atoms strongly interact in a bonding fashion to form a large delocalised pi-electron cloud stretch through the four orbitals. Note that the briding chloride p-orbitals are not in the same orientation as the terminal ones, but the geometry of the molecule allows the orbitals to be in-phase. A nodal plane now stretches across this pi-system. The p orbital of the Br atoms are out of phase with the other orbitals. However the orbitals are too small (most likely the 2p orbitals c.f. 3p) so only very weakly interact with the pi-system in an anti-bonding fashion. Excluding the atomic orbital nodes, a total of 3 nodes are present. The p orbitals of the briding Cl atoms form a sigma bond (relatively strong interaction) with each other across the internuclear space. However the two terminal Br p-orbitals are not in the correct orientation w.r.t. the the bridging p-orbitals so do not interact (no distortion of p-orbital lobe shape). The two Cl p-orbitals however are out-of-phase and are thus anti-bonding to the sigma bond orbital. Excluding the atomic orbital nodes a total of 2 nodes are present. Similarly to MO 73, the bridging chloride p orbitals are at the right orientation to from a sigma bond (v. strong) and form a large electron cloud in the internuclear spacing. This allows the p orbitals of the terminal Cl atoms to interact with this electron cloud in a bonding fashion as illustrated above (this interaction is relatively weak as the orbitals are small suggesting poor orbital overlap). The Br orbitals however, are not in phase with the system and those are anti-bonding as seen by the slight distortion of one of the lobes. Again excluding the atomic orbital nodes, a total of 2 nodes are present. This MO is essentially the opposite of MO 77 where the orbitals are oriented in the same way as MO 77. However the terminal Cl orbitals are oriented in-phase with the bridging orbitals which ultimately results in sigma antibonding interation between the bridging halide orbitals and pi anti-bonding interactions between the terminal orbtials and bridging orbitals with total of 5 nodes being formed as illustrated in the theoretical MO above (this is excluding atomic orbital nodes). The sheer number of nodes gives an indication of the degree of antibonding in this MO. The bridging halide orbitals are oriented such they they form a pi- antibonding interaction with each other creating a nodal plane in the internuclear spacing. The terminal orbitals are oriented orthogonally to the bridging orbtials, and as such do not interact with the orbitals (a slight distortion of the lobes can however be observed). Again the bromide orbitals are small so any interaction would be very weak. Note however that despite the terminal orbitals being in-phase, the lack of distortion suggests that there is very little to no through space interaction. ***Note that based on analysis of all the computed occupied non-core MOs it was determined that there is no indication of through space interaction apart from the interaction between the two bridging orbitals. This is based on the observation that despite through space orbitals being oriented in-phase to from bonding interaction, the orbitals did not show any form of distortion strongly suggesting that any through space interaction is too weak to be observed so considered not to exist in the AlBr2Cl4 dimer. This is possibly due to large bond distances and poorly matched orbitals. References