Rep:Mod:yh09mod1

The basic techniques of molecular mechanics and semi-empirical molecular orbital methods for structural and spectroscopic evaluations

The Hydrogenation of Cyclopentadiene Dimer

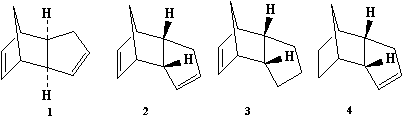
The dimerisation reaction of cyclopentadiene to form the dimer is a cycloaddition reaction, specifically the Diels Alder reaction. An endo or exo product can form and it is a matter of thermodynamic versus kinetic control. The exo product is found to have a total energy of 133 kJ/mol compared to the endo product with a total energy of 142 kJ/mol. Despite the exo product having the lower total energy, it is the endo product that is formed. The implies that the endo product is the kinetic product whereas the exo is the thermodynamic product. The reason for favouring the product containing the endo relationship between the two alkenes in the dimerisation product is due to orbital interations. As the cyclopentadiene molecules approach each other, the frontier orbitals in the cyclopentadiene are correctly aligned to form a sigma bond. There are also favourable interactions across space between the other orbitals even though no bonds are formed, through secondary orbital interactions.

Product 1, Exo dimer, Thermodynamic Product

Product 2, Endo dimer, Kinetic Product

Product 3

Product 4, Hydrolysis Product

Whilst the dimerisation to form the cyclopentadiene dimer is under kinetic control, the hydrogentation of the product is under thermodynamic control. Initially only one of the double bonds is hydrolysed and the process is under regioselective control. Therefore hydrogenation proceeds to give the product that is lower in total energy, i.e. the product that is less strained in the thermodynamic sense. The hydrogenation product has the double bond in the six-membered ring hydrolysed. This product has a total energy of 131 kJ/mol. When the alternative double bond has been hydrolysed, the total energy is 149 kJ/mol.

Comparison of product 3 and 4

Contribution to relative stabilty	Product 3 kJ/mol	Product 4 kJ/mol
Strectching	5.3	4.5
Bending	82.9	60.7
Torsion	45.6	52.3
1,4 van der Waals	23.6	18.8

The main difference that can be seen when comparing the steric energy terms is in the bending and 1,4 van der Waals energy. They state that the steric energy of molecule 3 is higher than molecule 4 and this justifies why 4 is formed in the hydrogenation reaction. The bend term is much higher in product 3 which implies that some bond angles have been deformed from their optimum bond angle to relieve some strain in the molecule. The programme defines the 1,4 van der Waals term as the energy for the through-space interaction of atoms separated by two atoms. The larger value for molecule 3 means that there are more steric clashes in the molecule which raises the overall energy of the product compared molecule 4.

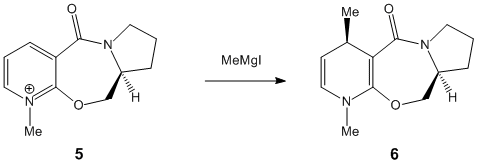
Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)

Two reactions will be studied in this section. They are both controlled by different interactions and the orientation of the carbonyl bond with respect to the ring varies.

Chelation

Molecule 5, 151kJ/mol

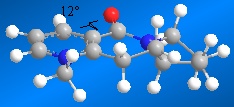The lowest total energy for molecule 5 is achieved when the carbonyl group is above the plane relative to the aromatic ring. In the reaction of prolinol with methyl magnesium iodide, the pyridine ring is alkylated in the 4-position, with the methyl on the top face of the ring. This is because the magnesium of the nucleophile chelates to the carbonyl. The carbonyl then has a directing effect, so the methyl group is on the same face as the carbonyl. The dihedral angle between the carbonyl group and the ring was calculated to be 12° and clearly shows that the group is above the ring. The molecule is aromatic and highly conjugated which means that the minimisation process is relatively fast. It showed that it was not possible for the carbonyl to be below the ring, but this does not take into account chelation control with the Mg. An improvement would be to model the transition state which is beyond the scope of MM2, which is unable to recognise Mg as an atom. Using a programme such as QST2 would be more suitable for minimising the total free energy of a transition state.

Lone pair repulsion

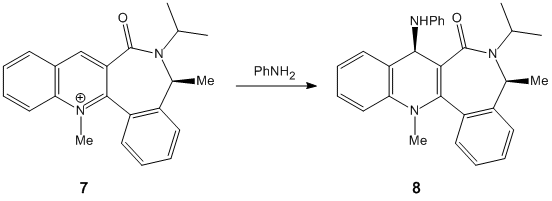
On the other hand, molecule 7 has its lowest total energy of 264 kJ/mol when the carbonyl group is on the opposite face to where the NHPhenyl group is attached, i.e. below the plane of the ring. In this case, the nucleophile does not contain a metal so chelation is no longer in effect. The aniline nucleophile and the carbonyl group both contain lone pairs on the C and O atom respectively. This lone pair repulsion causes the incoming nucleophile from the top face of the ring since the carbonyl group is on the opposite face. Several minimisation calculations had to be run when the programme was trying to find the lowest total energy of the molecule. The value obtained can only be compared to isomers of molecule 7, and not with molecule 5 since this contains different atoms.

Molecule 7, 360 kJ/mol

Molecule 7, 264kJ/mol

These two isomers of molecule 7 are given as an example of how the orientation of a group can change the calculated energy for a molecule. The isomers both have the carbonyl group below the ring, shown by the dihedral angle of 20°, and differ in the orientation of the alkyl group attached to the N, which is in the plane of the ring in higher energy isomer, and below the plane of the ring in the other isomer. This subtle change has affected the total energy value by 97 kJ/mol but when the carbonyl group was above the plane of the ring, the total energy was over 800 kJ/mol. Therefore the carbonyl position has the largest effect on total energy.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

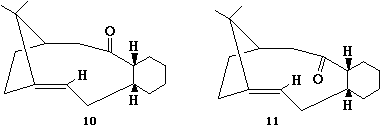
The total energy for isomers 10 and 11 were found. The lowest energy isomer was number 11, so this is the thermodynamic product. Initially, isomer 10 was formed, the kinetic product, which upon standing isomerises to product 11.

The process for determining the most stable isomer was difficult because MM2 only finds the local minimum for total energy rather than the global minimum. Therefore the values obtained are restricted by the conformation in which they were first drawn in 2D. You have to manually alter the position of the carbonyl group relative to the plane of the ring. However, this was not proficient as the carbonyl group reverted back to its initial position. The process to obtain the minimum total energy was time consuming and produced some very unreasonable and varying results. The highest minimised total energy found for intermediate 11 was 762 kJ/mol compared to the lowest value of 184 kJ/mol. For intermediate 11, the highest value obtained was 535 kJ/mol, compared to the lowest of 243 kJ/mol. To further improve the minimisations, the cyclohexane ring should be manipulated to see what effect this causes as 6 membered rings generally prefer to adopt the chair conformation.

Intermediate 11 Lowest Energy conformation

Taxol 10

Intermediate 10 Lowest Energy conformation

Taxol 11

Hyperstable Alkene

The alkene bond in the taxol intermediate reacts slowly due to it being a hyperstable olefin. The double bond is placed at the bridgehead of a bridged ring system, and Bredt's rule states that elimination to give a double bond at this position is unfavourable, with the product unstable and synthetically less accessible. This intermediate contradicts Bredt's rule because it involves a larger cyclic ring system, and has a negative olefin strain energy. OSE is defined as the difference in the strain energy of an olefin compared to the saturated hydrocarbon. The stability of the olefin is due to the special stability afforded by the structure and the greater strain of the parent hydrocarbon.

Modelling using semi emperical molecular orbital theory

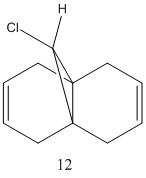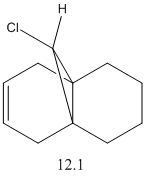The first part of the exercise used the purely mechanical molecular model to predict the reactivity and selectivity of chemical reactions. In this example, quantum mechanics will be used to consider the electrons in the nucleus and their effects on reactivity. Molecule 12 will be modelled using first using molecular mechanics and subsequently treated quantum mechanically.

The initial molecular mechanic, MM2 technique used to minimise the molecules took ~10 seconds whereas the subsequent MOPAC minimisation took nearly a minute. This time difference has to be considered in terms of better minimisation vs. a less expensive, shorter calculation period.

Orbitals of molecule 12

HOMO

HOMO-1

LUMO

LUMO+1

LUMO+2

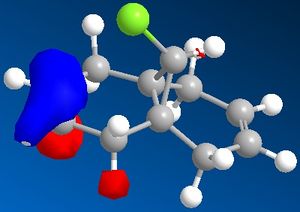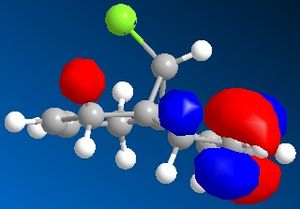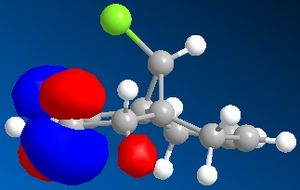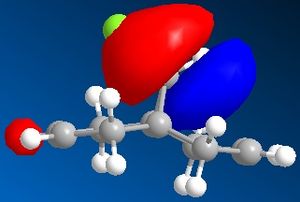
Molecular Orbitals can be obtained from the programme. The HOMO and LUMO are the frontier orbitals and examination of them can indicate which double bond is the most nucleophilic. The HOMO shows that the molecular orbitals are largest on the C=C bond anti to the C-Cl. This contains the highest density of electrons and negative charge and is the most nucleophilic double bond.

By examination of the HOMO-1, the LUMO, LUMO+1 and LUMO+2, it can be seen that the programme has discriminated between the two double bonds. They have different molecular orbitals due to them being either syn or anti to the C-Cl bond. When IR analysis is run on molecule 12 and 12.1, which has the C=C bond anti to the C-Cl bond hydrogenated to a C-C bond. The frequencies of the C=C and C-Cl bonds were found for both molecules and compared to eachother. These stretches, and the wavenumber at which they occurred were recorded. The C=C stretches occured at 1758cm^-1 for the syn C=C bond and 1737cm^-1 for the anti C=C bond.

As can be seen, the most significant difference in wavenumber is for the C-Cl bond. It is 770cm^-1 in molecule 12 and 775 cm^-1 in molecule 12.1. This means that the C-Cl bond in molecule 12 is weaker than in the monohydrogenated derivative because the wavenumber is proportional to the energy required to vibrate the bond, i.e. the bond strength. By studying the HOMO-1 and LUMO+1, this can be understood. The occupied π orbital of the C=C anti to the C-Cl bond is donating electron density to the antibonding orbital of the C-Cl bond. This means that the C-Cl bond in molecule 12 is weaker than the C-Cl bond in molecule 12.1.

Table showing vibrations of product 12 and 12.1

Bond	Product 12	Product 12.1
C-Cl
C=C syn to C-Cl
C=C anti to C-Cl

Structure based Mini project using DFT-based Molecular orbital methods

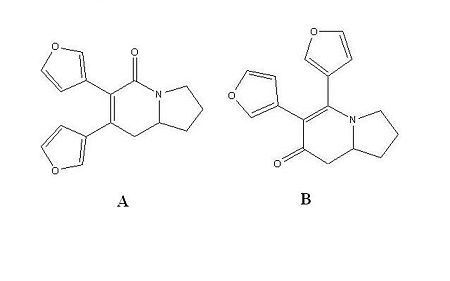
Two constitutional isomers, 7-di(furan-3-yl)-2,3,8,8a-tetrahydroindolizin-5(1H)-one, A, and 5,6-di(furan-3-yl)-2,3,8,8a-tetrahydroindolizin-7(1H)-one, B, were analysed in this project.

Isomer A

Isomer B

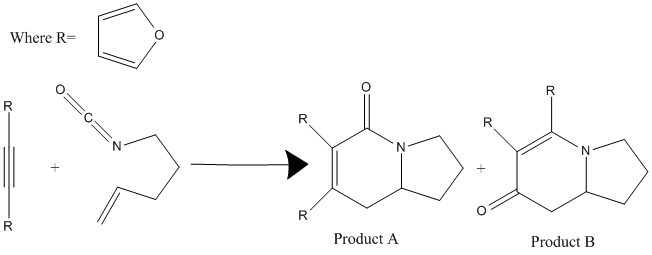
They are formed from the Rhodium-Catalyzed [2 + 2 + 2] Cycloaddition of Alkenyl Isocyanates and Alkynes in the reaction scheme shown on the left. The journal states that there is a slight preference for isomer B, with the products forming in a 1:1.1 ratio of A:B. The ¹³C NMR spectrum for both isomers was predicted using the GIAO approach which uses quantum mechanical density functional theory. The IR spectrum was also predicted. Both sets of spectral data was then compared to the literature data from the original paper. These are the most useful spectroscopic techniques for determining the different isomers because the connectivity and therefore functional groups present in the molecules differ. Isomer A contains the amide functionality whereas isomer B contains an enamine. Therefore ¹³C NMR and IR analysis are sufficient to differentiate between the constitutional isomers A and B. The following analysis relies on the belief that the reported literature values are correct.

Isomer A NMR

The full NMR data for isomer A, can be accessed at DOI:10042/to-2516

A

A

¹³C NMR Assignment for isomer A

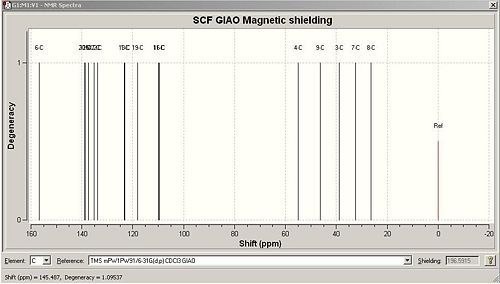C number	Computational ppm	Literature ppm	Difference between Literature and Computational value ppm
6	159.0	163.8	4.8
20	138.8	143.1	4.3
12	138.6	142.7	4.1
15	137.4	142.4	5.0
17	135.2	142.0	6.8
2	133.6	135.9	2.3
13	123.3	124.9	1.6
1	123.1	123.4	0.3
19	118.1	119.4	1.3
11	109.8	112.6	2.8
16	109.4	110.6	1.2
4	55.0	55.6	0.6
9	46.1	45.0	1.1
3	38.7	36.6	2.1
7	32.4	33.8	1.4
8	26.3	23.4	2.9

The ¹³C NMR peak list predicted by the computational method is very similar to the literature values. The difference between the shifts for each carbon is ~1ppm at the range 20-120 ppm. However, 120ppm there is a greater discrepancy between the literature and computed value, of ~5ppm which is still within the limit of experimental error. The carbonyl C has been shifted to a lower field compared with the rest of the C due to it being attached to the electronegative O atom. Although there is a discrepancy of 3.8ppm between the values, both chemical shifts falls into the expected range for a carbonyl carbon. There is a systematic error with the computational method for groups including amide carbonyls. Once this has been corrected using the formula:δcorr = 0.96δcalc + 12.2, the carbonyl shift of 159.0 ppm turns into 164.8 which is within 1ppm of the literature value.

Isomer B NMR

The full NMR data for isomer B, can be accessed atDOI:10042/to-2517

A

A

¹³C NMR Assignment for isomer B

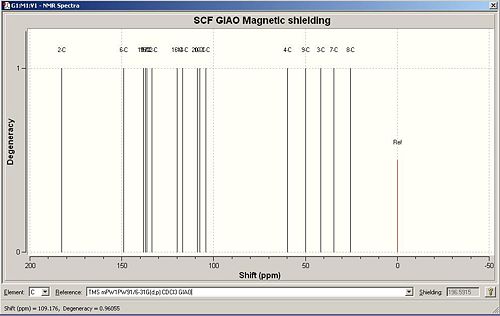C number	Computational ppm	Literature ppm	Difference between Literature and Computational value ppm
2	182.5	189.4	6.9
6	148.8	152.6	3.8
19	138.2	143.3	5.1
15	136.6	143.1	6.5
17	136.0	141.4	5.4
12	133.2	141.0	7.8
16	120.1	120.6	0.5
14	117.0	119.7	2.7
20	108.9	112.1	3.2
10	107.3	111.3	4.0
1	104.2	103.6	0.6
4	59.9	57.3	2.6
9	49.9	50.3	0.4
3	41.8	42.1	0.3
7	34.6	32.1	2.5
8	24.9	24.4	0.5

Again, there is a strong correlation between the predicted ¹³C NMR and the literature peak list. The differences between the values get larger when at the lower chemical shifts. The carbonyl C ppm differs from the literature value is due to a systematic fault with the computational calculation as mentioned above. Once this value has been corrected, the new value of 187.4 ppm is only different to the literature value by 2ppm. Orbital interactions between the C and O cannot be calculated by the programme so the limit of computational analysis has been reached. Despite this, it can be clearly seen that the GIAO approach can differentiate between the two isomers. It has also assigned the peaks which the literature paper did not do.

IR Analysis for Isomer A and B

Left Isomer A, Right Isomer B

IR Spectra, Isomer A

IR Spectra, Isomer B

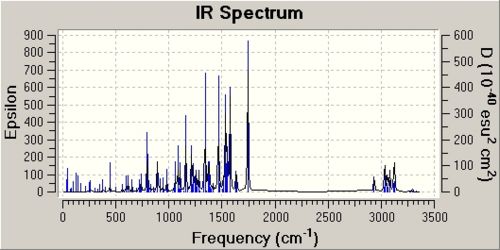The literature IR results were taken in solvent phase whereas the computational IR was run in the gas phase. Therefore there may be different interactions in space and solvent interactions which account for some differences in the IR spectrum. The literature reported the following information of isomer A: IR (NaCl, CHCl3) 1639, 1614, 1516, 1434, 1035 cm^-1. However, none of these peaks could be found in the computated IR spectrum. The literature value of 1639cm^-1 is indicative of an amide C=O, which is what the molecule contains. The corresponding C=O stretching frequency in the computated IR is found at 1735cm^-1, which is too high. From the minimised molecule for isomer A, the amide is puckered. This distortion means that the carbonyl is more akin to a ketone C=O than a amide C=O which can explain this anomaly. The literature only lists the most significant peaks in the IR and although the exact wavenumber does not match the computated value, the vibrations they correspond to are the same. To further improve this calculation, computational IR analysis of the molecule should be run in the same solvent as the literature solvent.

The literature reported for isomer B provided the following IR data: IR (NaCl, CHCl3) 1609, 1588, 1516, 1491, 1434, 1311, 1045 cm^-1. The only feasible C=O stretching frequency is 1609cm^-1, which is outside the typical range for all C=O stretches. The vibrations in the range 1400-1600cm^-1 are the aromatic C=C stretches. The vibration at 1311cm^-1 is most likely to be a C-N stretch or a H vibration. The corresponding vibrations from the computational IR analysis found the C=O stretch at 1743.58 cm^-1, C=C stretch at 1577cm^-1, C-H wag at 1340.5 cm^-1. The carbonyl stretch is what is expected of a ketone, and the other vibration frequencies are reasonable considering the different phase the IR was run in.

Mechanism for the formation of A and B

A

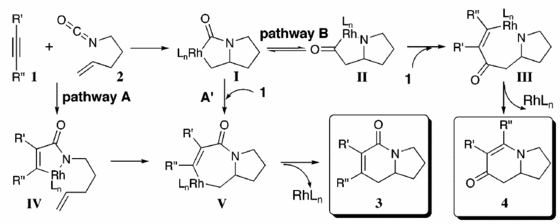
This mechanism scheme shows that the reaction is under kinetic control. Therefore comparison of the energy of the minimised molecules is not necessary and will not provide any reasoning to why isomer B is favoured to isomer A. The diagram to the left shows the proposed mechanisms for the formation of both isomers and they proceed via different pathways. For reactions when R is an aryl group, product 4 is favoured and when R is an alkyl group product 3 is favoured. This is consistent with what was found for the particular experiment I am studying but in my case, when R= furan, the products are formed in an approximately 1:1 ratio. This could be because both pathways are equally sterically demanding so there is no preference.

---

References and citations

---