Rep:Mod:yg0215
In this page optimization the NH3 molecule, and subsequent calculations with the N2 and H2 molecules are reported. Optimization on a hydroxide ion has also been carried out using a different basis set.
Optimization
In this task an NH3 molecule is analyzed using the B3LYP method.
The basis set was 6-31G(d,p).
The final energy reached was -56.55776873 a.u.
The RMS gradient is 0.00000485 a.u.
The point group of NH3 is C3V.
The "Item" table is as follows:
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986262D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
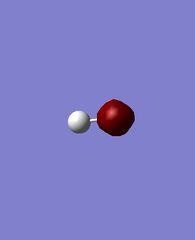
Ammonia |
N-H bond length:1.01798Å
H-N-H bond angle: 105.741°
A table showing that the molecule's energy has indeed been minimized can be found here.
Vibration and Charges
From the 3N-6 rule we expect 3*4-6=6 vibrations.
Calling FoFJK, ICntrl= 100127 FMM=F ISym2X=1 I1Cent= 0 IOpClX= 0 NMat=1 NMatS=1 NMatT=0.
Full mass-weighted force constant matrix:
Low frequencies --- -0.0473 -0.0028 -0.0006 1.9225 7.7017 7.7020
Low frequencies --- 1089.5366 1693.9474 1693.9474
Diagonal vibrational polarizability:
0.1276755 0.1276760 3.2981628
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A1 E E
Frequencies -- 1089.5366 1693.9474 1693.9474
Red. masses -- 1.1800 1.0644 1.0644
Frc consts -- 0.8253 1.7996 1.7996
IR Inten -- 145.3814 13.5533 13.5533
Atom AN X Y Z X Y Z X Y Z
1 7 0.00 0.00 0.12 -0.07 0.00 0.00 0.00 0.07 0.00
2 1 0.00 -0.21 -0.53 0.76 0.00 0.00 0.00 0.15 0.26
3 1 0.18 0.11 -0.53 0.08 -0.39 0.22 0.39 -0.53 -0.13
4 1 -0.18 0.11 -0.53 0.08 0.39 -0.22 -0.39 -0.53 -0.13
4 5 6
A1 E E
Frequencies -- 3461.2932 3589.8170 3589.8170
Red. masses -- 1.0272 1.0883 1.0883
Frc consts -- 7.2510 8.2634 8.2634
IR Inten -- 1.0608 0.2711 0.2711
Atom AN X Y Z X Y Z X Y Z
1 7 0.00 0.00 0.04 0.08 0.00 0.00 0.00 0.08 0.00
2 1 0.00 0.55 -0.18 0.02 0.00 0.00 0.00 -0.75 0.31
3 1 -0.47 -0.27 -0.18 -0.56 -0.34 -0.27 -0.34 -0.17 -0.15
4 1 0.47 -0.27 -0.18 -0.56 0.34 0.27 0.34 -0.17 -0.15
There are two vibrations of the same frequency, occurring for 1693.95cm-1 and 3589.82cm-1 respectively. The IR spectrum intensities for all but the first two frequencies are too low to be observed.
The two vibrations of frequency 1693.95 cm-1 are bending vibrations, those of frequency 1089.54 cm-1, 3461.29 cm-1, 3589.82 cm-1 are stretching vibrations.
The vibrational mode of frequency 3461.29 cm-1 is highly symmetric, since all 3 of the N-H bonds move outwards simultaneously.
The vibrational mode of frequency 1089.54 cm-1 is known as the "umbrella" mode, since the bonds move outwards and the molecule becomes planar.
We can expect to see 2 bands in a spectrum of ammonia gas. A vibrational mode only shows up on IR spectrum if its dipole moment changes as it vibrates. In the case of the 3 vibrations which do not show up, there is a small intensity calculated anyway.
The charge on the N atom is -1.125, the charge on the H atom is 0.375. Since nitrogen is more electronegative than hydrogen, electron density will be attracted more towards the nitrogen atom, giving it a partial negative charge and hydrogen a partial positive charge.
Reactions and Orbitals
Optimization calculations of the same type as that done earlier for ammonia was performed on N2 and H2.
As we can see from the log files below, the structures have converged to an energy minimum.
For N2
| Calculation | B3LYP |
| Basis set | 6-31G(d,p) |
| Final energy | -109.52412868 a.u. |
| RMS gradient | 0.00000060 a.u. |
| Point group | D∞h |
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.401159D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
The vibrational frequency is 2457.33 cm-1.
For H2
| Calculation | B3LYP |
| Basis set | 6-31G(d,p) |
| Final energy | -1.17853936 a.u. |
| RMS gradient | 0.00000017 a.u. |
| Point group | D∞h |
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
The vibrational frequency is 4465.68 cm-1.
We can now calculate the energy of each molecule.
E(NH3)=-56.55776873 a.u.
E(H2)=-1.17853936 a.u.
E(N2)=-109.52412808 a.u.
ΔE=-0.0557913 a.u. or -146.4800582 kJ/mol.
This tells us the product, ammonia, is more stable with respect to the reactants.
Choosing a molecule to analyze
OH- was analyzed in this task. The information obtained from the optimization are as follows.
| Calculation | B3LYP |
| Basis set | 6-31G(d,p) |
| Final energy | -75.72629185 a.u. |
| RMS gradient | 0.00000199 a.u. |
| Point group | C∞v |
Charge Distribution
The charge on O and H is -1.285 and 0.285 respectively.
Vibrations
Since this is a diatomic molecule, there is only one type of vibration, which occurs at a frequency of 3497.69 cm-1.
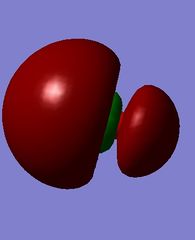
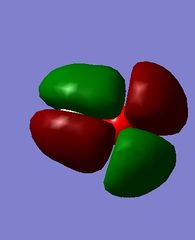
MOs of hydroxide ion
The images above show the HOMO and the LUMO respectively. We can see that the LUMO is anti-bonding, as there is no electron density between the MOs. There is a node in the electron density of the LUMO, suggesting it is formed from a 2s and 1s orbital overlap. The HOMO has π character as it is zero density at a nodal plane, and this suggests it is formed from 2p orbital overlap.
This is the MO which is the lowest in energy, at -18.66439 a.u. Electron density is concentrated on the oxygen atom.
This is an MO of energy equal to that of the HOMO. The shape is the same, however we can see that it is orientated in a different direction. This is due to the existence of 3 2p orbitals all pointing orthogonal to each other.
This is a high energy MO, being the 7th MO above the LUMO, with an energy of 2.00566 a.u. It is anti-bonding in character, since no mutual electron density is seen between the two atoms.
Appendix
Further exploration of computational methods
What are basis sets?
The basis set chosen is composed of Gaussian type orbitals. Alternatively, calculations can also be carried out using Slater type orbitals. A basis set contains functions which approximate the shape of the atomic orbitals. These functions are then combined to calculate the MO's which are here presented.[1]
Carrying out the same calculations for MOs using STO-3G instead gives only 6 MOs, compared to 20 for 6-31G(d,p). This is because the basis set is smaller, so less MO combinations are formed. The HOMO and LUMO plotted using this basis set are shown below.
 LUMO - the shape of this MO looks slightly different from the previous one.
LUMO - the shape of this MO looks slightly different from the previous one.
Links to log files and other references
- ↑ Introduction to Computational Chemistry, F. Jensen, 2nd Ed.