Rep:Mod:yf04q3

Yasser Farhat, 3^rd Year Computational Lab, Physical Module

Introduction

In this module, we hope to achieve a great understanding in transition state modelling in GaussView v.5. A transition state is define a hypothetical state that corresponds to the state a 'peak' of a potential energy along with its reaction coordinate . A transition state of a reaction is not isolatable nor can we identify them via spectroscopic analysis, as they only in a concerted transformation of a reaction, so essentially have an instantaneous lifetime.

Figure1- Energy profile

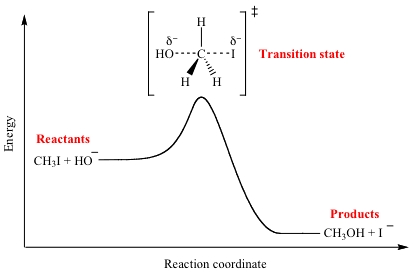
Figure 1 shows an example of a transition state in a energy profile, as just a maximum.

Appendix 1: All energies are quoted in Hartree au units unless otherwise stated (1 Hartree au = 2625.50 kJmol-1 = 627.51 kcalmol) . A calculation is considered successful if the RMS gradient value is less than 0.0001

Cope Reaction

Using the Cope rearrangement of 1,5-hexadiene, we will look at is reactive mechanism, via possible transition states. It is a [3,3] signmatropic shift, shown in figure 2, where the allyl group in 1,5-hexadiene is shifted. The sigmatropic process involced six electrons (aromatic due as it agrees with the 4n+2 aromatic rule). the shift is thermally allowed via Huckel topology with suprafacial components .

Figure 2 - Cope rearrangement of 1,5-hexadiene

Whether it went via a concerted, stepwise or dissociative mechanism was under discussion for a long time but it is now generally accepted that it goes in a concerted fashion via either a C2h "chair" or C2v "boat" transition structure where ging via the "chair" transition structure being the more stable transition route.

The objective of this experiment is to locate the low-energy minima and transition states to determine which reaction mechanism is preferred; the DFT: B3LYP (6-31G*) method has been shown to calculate this reaction in good agreement with experimental data.

Optimization of 1,5 Hexadiene conformers [HF/3-21G]

In this section we optimized several conformers of 1,5 Hexadiene, which included Six gauche conformers (dihedral angle = 60°) followed by four antiperiplanar (dihedral angle = 180°). To rationalise the mechanism by which the Cope rearrangement occurs, the optimised geometries and their energies where analysed. Due to symmetry of the molecule and entiomerism of the conformers only 10 are energetically distinguishable .

Each conformer was constructed and optimized in GaussView, for each Antiperiplanar and Gauche conformer the C1-C2-C3-C4 and C3-C4-C5-C6 angle and H1-C1-C2-H2 and H5-C5-C6-H6 dihedral angel was altered slighted to give derivative conformers of each main conformer. This was done by the dihedral angle tool.

The low level basis set 3-21G was initially used with the Hartree-Fock method to do a basic optimisation. The point group was determined using the Symmetrize function and was then noted along with the energy in a.u. (Hartrees). Details of the calculations and results and shown in the table below. Energies given to 5 decimal places

Conformer/J-Mol	Structure	Point Group	Energy Calculated/a.u.	Gradient	Relative Energy/ kcal/mol	Log File
		C2	-231.68772	0.00000173	cell	File:Gauche yf 1.log
		C2	-231.69167	0.00000456	cell	File:Gauche yf 2.log
		C1	-231.69266	0.00001176	cell	File:Gauche yf 3.log
		C2	-231.69153	0.00002085	cell	File:Gauche yf 4.log
		C1	-231.68962	0.00001489	cell	File:Gauche yf 5.log
		C1	-231.68916	0.00000894	cell	File:Gauche yf 6.log
		C2	-231.69260	0.00000542	cell	File:Anti yf 1.log
		Ci	-231.69254	0.00002664	cell	File:Anti yf 2.log
		C2h	-231.6890	0.00001547	cell	File:Anti yf 3.log
		C1	-231.69097	0.00001454	cell	File:Anti yf 4.log

All conformers where successfully optimized and all matching the Appendix 1 criteria, it appears that conformer 'Gauche 3' has the lowest relative energy. This can be explained by MO interactions. Also its found that all the APP conformers are lower in energy then all the other Gauche conformers. This can be rationalised by the minimal steric hinderance experienced in Anti-periplanar conformers, with respect to Gauche, lowering the overall energy of the APP molecules via less steric strain.

Comparing my Ci Anti 2 conformation energy (-231.69254 a.u.) with Mike Bearparks energy (-231.69254 a.u.). I am happy optimized was done correctly, and the right values where obtained for each optimization.

MO analysis of 3 lowest energy HOMO'S

For the MO analysis, the 3 lowest energetic conformers are Gauche 3, APP 1 and APP 2, respectively. The MO analysis was to compare the HOMO orbitals of each conformer and comparing each one stating why gauche 3 has the lowest energy out the 10 possible 1,5 Hexadiene conformers. For the MO analysis to take place, each 3-21G optimzed conformer was opened and re-saved under its current file name with 'MO' added to the end. The calculation setup was straight forward, the 'job type' was changed from 'Optimization' to 'Energy'; under the NBO tab, the 'type' drop down tab was changed from 'None' to 'FULL NBO'; lastly adding 'pop=full' in the additional keywords section. This was done to each conformer and was submitted. Now the calculated MO where ready for analysis.

Table 2 - HOMO analysis

Conformer	HOMO Molecular orbital	Relative energy\ kcal mol-1	MO .log file
Gauche 3		0.00	File:Gauche 1 MO.log
APP 1		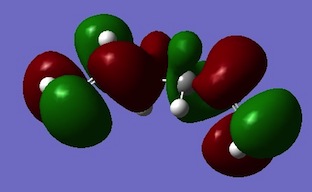0.04	File:App 1 MO.log
APP 2		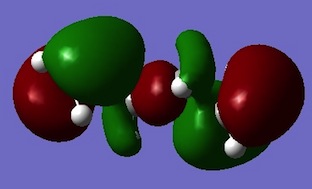0.05	File:App 2 MO.log

Despite Gauche 3 sterically less favoured then the APP conformers, its most lowest energy can be rationalised by its electronic. Above the HOMO for Guache 3 π-bonds of the C=C bonds are lying criss-crossed over each other in this conformer. This promotes effectual π-molecular orbital overlap and hence stabilises the molecule. The other HOMO molecular orbitals show more nodes within the π-bonds. .

Optimization of 1,5 Hexadiene Anti 2 conformers [B3LYP/6-31G(d)]

The basis set HF/6-31G(d) is a higher basis set then the HF/3-21G, meaning less approximations to the schrodinger equation during the calculations. So output information will be accurate.

Anti 2 Optimization using higher basis

APP 2
File Name	app_2_631g
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d)
Charge	0
Spin	Singlet
E(RB3LYP)	-234.61170618 a.u.
RMS Gradient Norm	0.00003720 a.u.
Imaginary Freq
Dipole Moment	0.000 Debye
Point Group	CI
Job cpu time	0 mins 31.1 secs.

Comparison of Anti 2 C-C Bond lengths
Basis Set	Geometry	C1-C2 Bond Length/Â	C2-C3 Bond Length/Â	C3-C4 Bond Length/Â	C4-C5 Bond Length/Â	C5-C6 Bond Length/Â
HF/321-G		1.35520	1.54000	1.54000	1.54000	1.35520
RB3LYP/631-G(d)		1.33351	1.50424	1.54835	1.50424	1.33351

Comparison of Anti 2 C-C-C Bond Angle
Basis Set	C1-C2-C3 Bond Angle/°	C2-C3-C4 Bond Angle/°	C3-C4-C5 Bond Angle/°	C4-C5-C6 Bond Angle/°
HF/321-G	124.802	111.343	111.343	124.803
RB3LYP/631-G(d)	125.278	112.665	112.665	125.278

The energy difference between the two difference basis sets is 2.919166 a.u. which is equivalent to 1831.80471 kcal/mol, indicating the difference in accuracy between the HF/31-G and RB3LYP/631-G(d) basis set.

Frequency Analysis of Anti 2 conformers [B3LYP/6-31G(d)]

Frequency analysis was done using the [B3LYP/6-31G(d)] optimised file, the job type was changed from 'Optimization' to 'Frequency' and submitted.

Full mass-weighted force constant matrix:
Low frequencies ---  -7.8842   -6.2548   -0.0007    0.0005    0.0005    6.9259
Low frequencies ---   75.0176   80.1190  120.0281

Anti 2 shows no low frequency under -10, indicating a they might be fully converged. The second row frequencies are a magnitude greater than the top row frequencies which is expected. Also, resulting vibrational modes were all positive, this confirms that the conformer is a local minimum along the potential energy surface. Frequency analysis takes the second derivative of the potential energy surface; hence as they are all positive, the end point was a minimum rather than a maximum indicating a transition state.

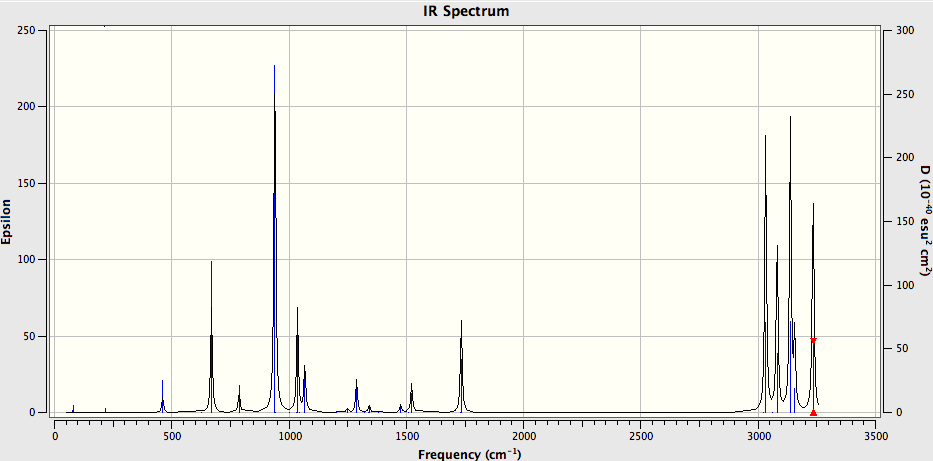
Half of 42 vibrational modes are IR active.

Anti 2 IR spectra

Anti 2 Frequency Table

Vibration Mode	Frequency/ cm -1	Intensity/ 1040 esu2 cm 2
1	75.02	0.0313
2	80.12	0.1082
4	219.33	0.1593
7	461.26	2.8987
9	669.32	19.9237
10	787.12	4.1536
11	937.92	9.5260
13	939.95	64.1659
17	1035.92	19.5865
19	1067.17	9.5867
21	1250.32	0.8050
22	1287.87	6.3059
25	1341.74	1.4480
28	1475.56	1.5179
30	1522.55	5.6269
32	1734.26	18.1174
34	3013.70	53.4603
36	3080.66	35.7076
38	3137.06	56.1677
39	3155.59	14.7458
42	3234.13	45.4841

The peaks of interests are the ones that correspond to the symmetric and asymmetric stretches of the 2 double bonds. Which are shown in the table below:

Vibrational Mode	Frequency (cm-1)
31	1731.06 (symmetric)
32	1734.26 (asymmetric)

Thermochemistry of Anti 2

Thermochemistry data where obtained from the results file from the frequency analysis:

Zero-point correction=                           0.142466 (Hartree/Particle)
Thermal correction to Energy=                    0.149821
Thermal correction to Enthalpy=                  0.150766
Thermal correction to Gibbs Free Energy=         0.110877
Sum of electronic and zero-point Energies=           -234.469240
Sum of electronic and thermal Energies=              -234.461885
Sum of electronic and thermal Enthalpies=            -234.460941
Sum of electronic and thermal Free Energies=         -234.500829

Recalculated at 0K:

Zero-point correction                               0.142944 (Hartree/Particle)
Thermal correction to Energy                        0.142944
Thermal correction to Enthalpy                      0.142944
Thermal correction to Gibbs Free Energy             0.142944
Sum of electronic and zero-point Energies           -234.468766
Sum of electronic and thermal Energies              -234.468766
Sum of electronic and thermal Enthalpies            -234.468766
Sum of electronic and thermal Free Energies         -234.468766

Optimization of Chair Transition structure

First Approach: Optimization with Berny Algorithm

The Berny alorithm is a default method developed by Bernhard Schlegel. Its method predicts the most stable sturcture from the forces acting on the atoms along with Hessian Matrix. Method constructs an approimate Hessian, allowing a quicker calculating time.

The chair was optimised using the 'Optimization to a TS (Berny)' method with the additional keyword 'Opt=NoEigen' with the Hartree-Fock (3-21) method. Frequency analysis of the output showed an imaginary vibration at 817.93cm-1, characteristic of the transition state.

The distances between the terminal carbons were 2.02Å

File:Chair opt guess yf.log

Berny Optimized chair transition structure

Vibration Mode of Imaginary Frequency
Calculation Type	FREQ
Calculation Method	RHF
Basis Set	3-21G
Spin	Singlet
E(RB3LYP)	-231.61932248 a.u.
RMS Gradient Norm	0.00000047 a.u.
Imaginary Freq	1
Dipole Moment	0.000 Debye
Point Group	C2H
Keyword	Opt=NoEigen
Number of Imaginary Frequency	-817.93 cm-1
Job cpu time	0 mins 13.1 secs.

Second Approach: Frozen Coordinates Method

The transition state was then reoptimised using the frozen coordinate method. This works by first optimising the structure to a transition state (Berny) with the bond forming carbons frozen. Following this, it is reoptimised, but instead the frozen bonds were now optimised as derivatives. The distances between the terminal bond forming carbons were again 2.02Å.

File:Frozen chair yf.log

Frozen Coordinates Method of chair transition structure

Vibration Mode of Imaginary Frequency
Calculation Type	FREQ
Calculation Method	RHF
Basis Set	3-21G with Freeze coordinates
Spin	Singlet
E(RB3LYP)	-231.61932244 a.u.
RMS Gradient Norm	0.00002334 a.u.
Imaginary Freq	1
Dipole Moment	0.0004 Debye
Point Group	C2H
Keyword	Opt=ModRedundant
Number of Imaginary Frequency	-817.93 cm-1
Job cpu time	0 mins 13.1 secs.

Third Approach: Calculations with Derivative and IRC

Given the structure of transition state being optimized correctly, it does not mean that mean that the resultant structure is the actual connection between reactant and product. Intrinsic reaction coordinate (IRC), which is defined as the minimum energy reaction pathway (MERP) in mass-weighted cartesian coordinates between the transition state of a reaction and its reactants and products, will be used in this part. It can be thought of as the path that the molecule takes moving down the product and reactant valleys with zero kinetic energy.

In this stage, 50 is set to be the number of points and force constant is always calculated. Additionally, since the reaction coordinate is symmetric for chair conformer, only calculation on the forward direction is carried out whereas generally both directions will be taken into consideration.

1. Derivative File:Derivative yf.log

Calculations with Derivative chair transition structure

Vibration Mode of Imaginary Frequency
Calculation Type	FREQ
Calculation Method	RHF
Basis Set	3-21G with Derviativew
Spin	Singlet
Energy	-231.61932201 a.u.
RMS Gradient Norm	0.00005434 a.u.
Imaginary Freq	1
Dipole Moment	0.000 Debye
Point Group
Keyword	Opt=ModRedundant
Number of Imaginary Frequency	-818.03 cm-1
Job cpu time	0 mins 26.1 secs.

2. IRC Calculations

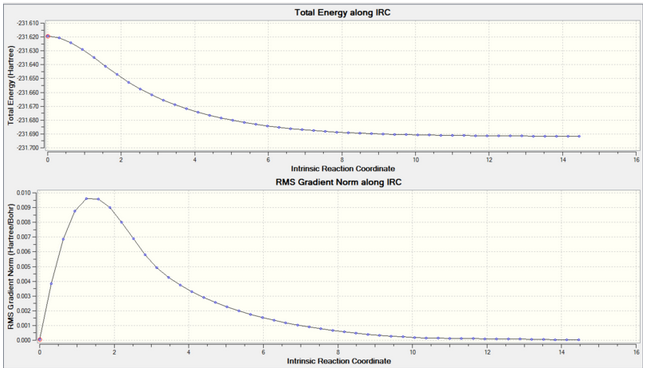
Intrinsic reaction coordinate (IRC) was used to confirm which chair transition structure is used. The calculations take the structure to a minimum via small atomic coordinates changes to follow the potential energy surface downwards. The analysis was performed on the chair transition state generated from the frozen coordinate method and was only performed in one direction due to the reactant and product being the same. This was done in 50 steps and the force constants were always calculated for each step.

File:IRC YF.log

Calculations with Derivative chair transition structure

Vibration Mode of Imaginary Frequency
Calculation Type	FREQ
Calculation Method	IRC
Basis Set	3-21G with Derviativew
Spin	Singlet
Energy	-231.69157866 a.u.
RMS Gradient Norm	0.00001534 a.u.
Imaginary Freq	1
Dipole Moment	0.3630 Debye
Point Group
Number of Points	50
Number of Imaginary Frequency	-818.03 cm-1
Job cpu time	0 mins 26.1 secs.

2b. Energy and RMS Gradient graph:

From the IRC, we can see that the RMS gradient has nearly 0 meaning that the TS was fully minimised.

Optimization using higher basis set

File:Chair higher basisset.log

Optimization using higher basis se

Calculation Method	Optimization to a TS (Berny)+ Frequency Analysis
Basis Set	B3LYP/6-31G*
Spin	Singlet
Energy	-234.5569830 a.u.
RMS Gradient Norm	0.00005434 a.u.
Imaginary Freq	1
Number of Imaginary Frequency	-565.53 cm-1
Job cpu time	6 mins 22.1 secs.

Frequency analysis of the structure showed one imaginary frequency at -565.53^cm-1 confirming the structure is a transition state.

Results:

Parameter	HF/3-21G	B3LYP/6-31G(d)	Literature Value
C1-C2 Distance/ Å	2.3736	2.3736	1.599
C4-C5 Distance/ Å	2.4452	2.4452	1.899
C2-C3 and C5-C6 Bond Length/ Å	1.4075	1.4075	1.474
C3-C4 and C1-C6 Bond Length/ Å	1.4075	1.4075	1.382
C-H Bond Length/ Å	1.0886	1.0886	1.110
C4-C5-C6 Bond Angle	119.7048o	112.4944o	113.4o
C2-C3-C4 Bond Angle	107.4615o	103.6352o	106.4o
Dihedral Angle	64.0448o	65.1817o	N/A

Optimization of the boat structure

First attempt

In the first stage, optimization to TS (QST2) is used, which allows the optimization of the transition state given reactant and product specified. However, since it simply transfers the reactant to product without and consideration in the bond rotation, it could be inaccurate or even cause errors during optimization.

The previously optimized anti 2 conformer (Ci symmetry) is assumed to be both the reactant and product in this case. Atom numbered where manually changed

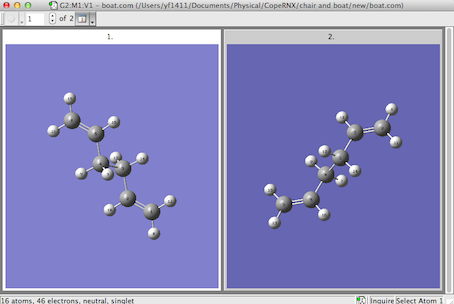
Infact the optmization failed given a transisiton structure similar to a 'chair' structure, below:

Second attempt

he reactant and product geometries were then altered so that they appeared closer to the boat transition structure by modifying the dihedral angles around the central four carbon atoms. After recalculation, this produced the structure shown in table 6, which clearly resembles a boat-like structure. The C2-C3-C4-C5 angle was changed to 0° and C1-C2-C3 and C4-C5-C6 angles where changed to 100°, shown below:

Frequency animation:

Energy and RMS gradient graph:

Activation energies:

Activation energies for Boat and Chair TS DFT-B3LYP/6-31G(d)

	Symmetry	Electronic & zero-point energies(a.u.)	DFT Electronic and Thermal Energies (a.u.)	Terminal bond forming carbon separation (Å)	Activation Energy(kcalmol-1) at 298.15K
Chair TS	C2h	-234.414929	-234.409008	1.97	34.12
Boat TS	C2v	-234.402342	-234.396008	2.21	42.02

Literature Results

Transition Structure	literature value (0K)
Chair TS	33.5 ± 0.5
Boat TS	44.7 ± 2.0

Calculations show similar values of activation energies to the literature values.

The Diels-Alder cycloaddition

The Diels-Alder cycloaddition was first described by Otto Paul Hermann Diels and Kurt Alder, which resulted in a Noble price in chemistry year 1950. It refers to a [4+2]-cycloaddition of conjugated diene and dienophile, its an electrocyclic reaction that involved a 4 π-electron from a diene and 2 π-electrons from a dienophile. These reactions are driven by the formation of a two new σ-bonds, which are energetically more stable then π-bonds.

Basic Diel-alder mechanism

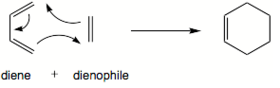
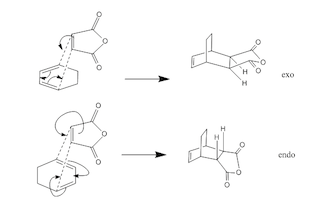
An unsymmetric dienophile results in two possible transition states, the endo and exo transition state (lead to different stereochemsitry). In the endo transition state the dienphile is orientated towards the diene π-system, and the exo transition state the dienophile is orientated away from the diene.

exo and endo products

In this experiment, studies of transition states in Diels Alder reactions will be achieved using quantum mechanic approaches. Unlike in analysis of cope rearrangement where Hartree-Fock and DFT have been developed, the AM1 semi-empirical molecular orbital method will be used in investigation. This method performs better in locating transition states, as well as being more effective, but bears the disadvantage of poor prediction on larger systems.

Two Diels Alder reactions will be covered in the following sessions, one of ethylene and cis-butadiene, the other one of cyclohexa-1,3-diene and maleic anhydride.

MO analysis

Ethene and Cis-Butadiene MO Analysis

As the cycloaddition can be explained using the HOMO and LUMO of the reactions we shall have a look at them. MO calculations for both Ethene and Cis-Butadiene where done using an AM1 semi-empirical molecular orbital method, to determine how the reactions proceeds.

Ethene and Cis-Butadiene Results

	Ethene	Cis-Butadiene
J-Mol
File Type	.log	.log
Calculation Type	FOPT	FOPT
Calculation Method	RAM1	RAM1
Basis Set	ZDO	ZDO
Energy (RAM1)	0.02619027	0.04879729
RMS gradient	0.00003334	0.00006203
Dipole Moment	0.0000	0.0418
Point Group	C2H	CS
.log file	File:Ethene YF.log	File:Cis-Butadiene YF.log

HOMO/LUMO of Ethene and Cis-Butadiene

	HOMO	LUMO
Ethene
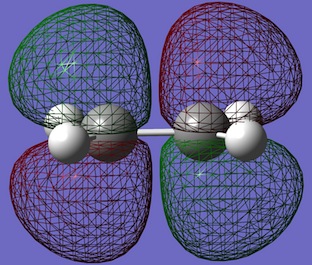
Cis-butadiene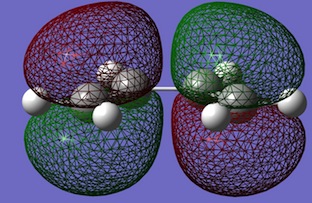

Symmetry of each orbital are explain relative the vertical and horizontal planes.

• Cis-Butadiene HOMO: Anti-symmetric in both planes
• Cis-Butadiene LUMO: Symmetric in vertical plane; anti-symmetric in horizonal plane
• Ethene HOMO: Symmetric in both planes
• Ethene LUMO: Anti-symmetric in both planes

Transition State MO Analysis

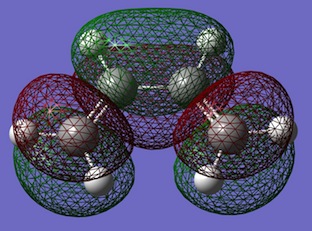
The transition state was built by using a bicycle[2.2.2]octane molecule found in the ring fragments tab and modified. modifications included removal of a CH₂-CH₂ bridge and replacing the C-C bonds with a C-H bond; Disconnecting C1-C2 and C3-C4 bond and modifying there bond lengths to 2.2 ; forming a C=C bond between C5-C6. Before optimization the disconnect bonds where frozen. Visual modifications can be seen below:

----->

Transition state results Results

J-Mol
File Type	.log
Calculation Type	FREQ
Calculation Method	RAM1
Basis Set	ZDO
Energy (RAM1)	0.11165465
RMS gradient	0.00000600
Imaginary Freq	1
Dipole Moment	0.5605 D
Point Group	C1
.log file	File:Diels-alder transition state1.log

HOMO/LUMO of Envelop Diels-Alder TS

	HOMO	LUMO
Diels-Alder TS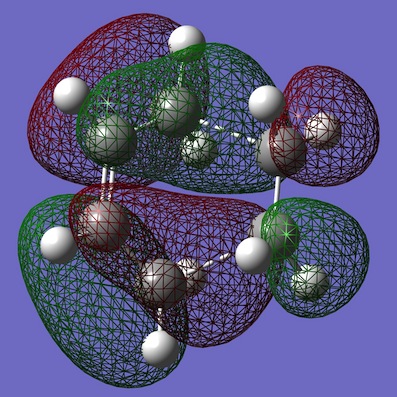

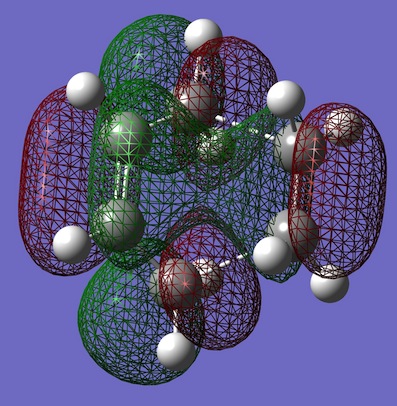
Computed energies of TS HOMO: -0.32494 a.u. and computed energy of TS LUMO: 0.02315 a.u. The transition state molecular orbitals can clearly show the overlaps formed are a result of a combination of the both ethene and cis-butadiene orbitals. It can been seen that the TS HOMO is a result of the combination of the cis-butadiene HOMO overlapping with the ethene LUMO orbital. While, the TS LUMO is shown to be a combination of cis-butadiene LUMO overlapping with the ethene HOMO. For the optimised reactants, the C=C bond lengths in the reactions are ~1.33Â and the C-C bond in cis-butadiene is 1.45Â. While in the TS the C=C bond has a length of 1.39Â (~1.4Â) as expected and all the other C-C bonds are 1.38Â as expected. The bond betwee the 'ethene' and cis-butadiene' is 2.12Â.

Deviations between the reactants and transition state are due to the slight delocalisation in the π-system. Below shows a the transition state with its bond distances (https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3#The_Diels_Alder_Cycloaddition)

Transition State Bond Distances

Transition State Frequency analysis

Frequency analysis of the TS shows an imaginary frequency at -956.14cm^-1, shows that a TS was formed. Another important frequency is the lowest positive frequency at 147.17cm^-1. Table below shows us the analysis of these frequencies:

Frequency	Vibrational Mode	Vibrational mode significance
-956.14cm-1		Shows the two fragments come together in a synchronous manner, relating to concerted bond formation
147.17cm-1		Shows the two fragments come together in an asynchronous manner, not relating to concerted bond formation

Optimization and Frequency calculations are valid, as shown from a section of the real output:

        Item               Value     Threshold  Converged?
Maximum Force            0.000017     0.000450     YES
RMS     Force            0.000004     0.000300     YES
Maximum Displacement     0.000351     0.001800     YES
RMS     Displacement     0.000073     0.001200     YES
Predicted change in Energy=-5.3223915D-08
Optimization completed.
   -- Stationary point found.

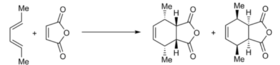
Study of regioselectivity in the Diels-Alder reaction

The Diels-Alder reaction of maleic anhydride and 1,3-cyclohexadiene reaction is subjected to regioselectivity which can form an exo (thermodynamic controlled)or endo (kinetic controlled) product. Reaction scheme shown below. The two different products are formed due to reaction mechanism go via two different TS. Similarly above the transition states will be modelled Optimization to a TS(Berny( and a semi-emperical AM1 method.

Firstly maleic anhyride and 1,3-cyclohexadiene where optimised using the B3LYP method and 6-31G(d) basis se, separately before beingg placed on the same page and orientated to represent the exo and edo transition states. The frozen coordinate method was adopted for the detection of the TS for this reaction as it was believed that both the TS berny method and QST2 method would struggle to determine the TSs. This was because the guess for the TS in both methods must be extremely similar to the actual structure of the TS to allow the programme any chance of detecting the correct TS.

Starting material results

	Maleic Anhydride	1,3-Cyclohexadiene
File Type	cell	cell
Calculation Type	.log	.log
Calculation Method	FOPT	FOPT
Basis Set	RB3LYP	RB3LYP
E(RB3LYP)	-379.28954456	-233.41893613
RMS Gradient Norm	0.00006069	0.00003473
Dipole Moment	4.0720	0.3776
Point Group	C1	C1
.log file	File:Maleic Anhydride YF.log	File:Cyclohexadiene YF.log

HOMO/LUMO or starting material

	Maleic Anhydride	1,3-Cyclohexadiene
HOMO	Symmetrical	Anti-Symmetrical
LUMO	Anti-Symmetrical	Anti-Symmetrical

Note that the Maleic HOMO does not interact with the diene LUMO, in fact the maleic HOMO-2 does instead due to its right symmetry.

Symmetrical

Locating Endo and Exo transition structure

Starting material results

	Exo	Endo
J-Mol
File Type	.log	.log
Calculation Type	FREQ	FREQ
Calculation Method	RB3LYP	RB3LYP
Basis Set	6-31G(d)	6-31G(d)
E(RB3LYP)	-612.67931	-612.68340
RMS Gradient Norm	0.00001714	0.00001227
Dipole Moment	55.071D	6.1141D
Point Group	CS	C1
.log file	File:Exo YF.log	File:Endo YF.log

Endo and Exo transition state MO

HOMO.LUMO of both Exo and Endo transition structure

MO label	EXO	Endo
HOMO	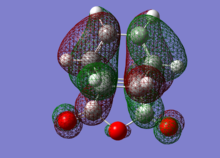Anti-symmetrical	Anti-symmetrical
LUMO	File:EX0 LUMO YF.jpg Anti-symmetrical	Anti-symmetrical

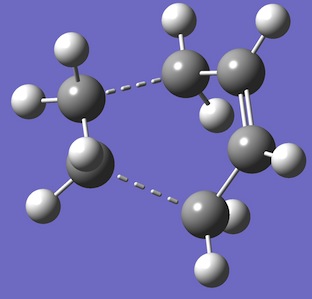
The HOMO of each describes the σ-bonding interaction to be formed between between the reagents. It is constructed by overlap of the HOMO of cyclohexadiene with the LUMO of the maleic anhydride. The LUMO of Maleic anhydride forms the π* anti-bonding orbital of the C=C bond. Because it is populated during the cycloaddition the C=C bond breaks, leaving a C-C single bond.

It is thought that the exo TS should be the more stable but the endo TS is however, the more stable of the two by 0.0041 a.u. This is due to secondary-orbital interactions in the endo TS which stabilise the structure[1]. These interactions are present between the central carbons of the conjugated π-system in the cyclo-1,3-hexadiene fragment and the π*-orbital of the C=O bonds from the maleic anhydride fragment. In-phase orbitals centred on the carbon atom of the π* C=O orbital and the central carbons of the conjugated system are able to interact creating an overlap present on the top face of the π-conjugated system from the back of the molecule to the bottom face of the maleic anhydride. The overall effect is to cause a stabilisation in the endo TS which lowers its Activation energy. The interaction can be seen in the thumbnail alongside and is demonstrated in the diagram below.

IRC

Exo and Endo IRC comparison

TS	IRC graph	IRC Visualisation	.Log File
EXO		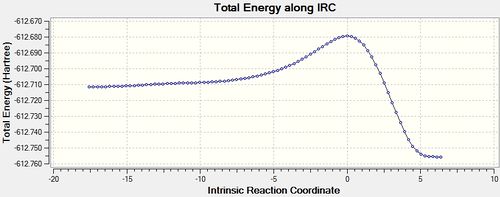	File:EXO IRC YF.log
ENDO		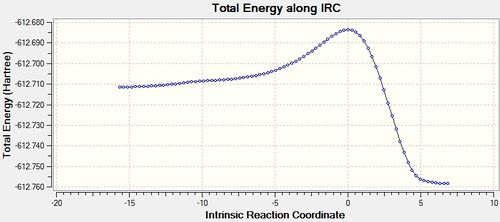	File:EXO IRC YF.log

The IRC shows that the transition state calculated is the one that connects the given reactants and desired products.

DFT/6-31G(d)	Maleic anhydride+1,3-cyclohexadiene	Endo TS	Exo TS
Sum of electronic and zero-point Energies	-612.52977	-612.50214	-612.49801
Sum of electronic and thermal energies	-612.51940	-612.49179	-612.48766
Sum of electronic and thermal free energies	-612.58644	-612.53833	-612.53427

Product	Endo	Exo
Ea 0K	0.02763	0.03176
Ea 298.15K	0.02761	0.031739
Ea 0K (kcal/mol)	17.336	19.917
Ea 298.15K (kcal/mol)	17.328	19.917

Conclusion

This project has been successful in introducing basic calculation methods for the study of the transition states in two sets of pericyclic reactions. It has been shown that for the Cope rearrangement the activation energy of going through the chair transition state is 8.225 kcal/mol lower in energy at room temperaure than the boat, implying that this is the favoured reaction route. The second part of the project has looked further into transition states of reactions where there are two possible products. It has been shown that for Diels-Alder reaction between maleic anhydride and 1,3-cyclohexadiene that orbital interactions through the transition state are key in the selectivity of the products.

Reference

<references>