Rep:Mod:yf04q2
Aromaticity:
Our main objective is to see how closely related a benzene MO picture is to our normal understanding of the MO orbitals in beneze. mainly looking at the π-cloud and how heteroatoms can alter the MO picture. the emerged pz orbitals in a aromatic benzene to give its π-clouds.
For each molecule computed in this section, the same method for each calculation was the same. For every optimisation the molecule was created using GaussView and was subjected to an optimisation calculation [OPT] using B3LYP as the method and a basis set of 6-31G(d,p). For every frequency the optimised molecule (B3LYP method and 6-31G(d,p) basis set) its job type was changed from Optimisation to Frequency, with no other changes and saved as a new file. For The Molecular Orbital the optimised molecule was opened and its 'NBO type' was changed from 'none' to 'FULL NBO' with the term 'pop=full' typed in the Additional Keywords section.
So, for each Optimisation, Frequency, MO, NBO calculations taken, the above instructions where done.
Benzene:
Optimisation:
Item Value Threshold Converged?
Maximum Force 0.000203 0.000450 YES
RMS Force 0.000078 0.000300 YES
Maximum Displacement 0.000824 0.001800 YES
RMS Displacement 0.000287 0.001200 YES
Predicted change in Energy=-4.355927D-07
Optimization completed.
The above shows that the 6-31G (d,p) optimisation was successful with both the force and displacements converging
| File Name | Benzene_opt_D6H |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -232.25821389 a.u. |
| RMS Gradient Norm | 0.00009009 a.u. |
| Imaginary Freq | |
| Dipole Moment | 0.0000 Debye |
| Point Group | D6H |
Bond Distance:
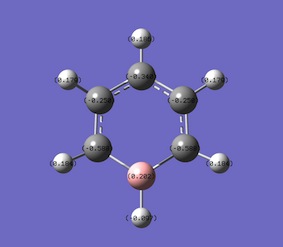
All c-c bonds distances are equal, as well as all C-H bonds.
C-C bond: 1.39621 Â
C-H bond: 1.08606 Â
Frequency
Low frequencies --- -2.5530 -2.5530 -0.0088 -0.0042 -0.0042 10.3930
Low frequencies --- 413.9723 413.9723 621.1358
Top row frequencies are all within 15 cm-1 of each other, and are an order of magnitude of the second row frequencies. This shows frequency calculation where correctly done.
Molecular Orbital analysis
| File Name | Benzene_MO |
| File Type | .log |
| Calculation Type | SP |
| Calculation Method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -232.25821389 a.u. |
| RMS Gradient Norm | 0.00009009 a.u. |
| Imaginary Freq | |
| Dipole Moment | 0.0000 Debye |
| Point Group | D6H |
Natural Bond analysis
The specific NBO charges for carbon and hydrogen were then analsyed. the charge distribution was set to NBO and carbon was sown to have a negative charge of -0.239 and hydrogen had a positive charge +0.239, as shown in the diagram.
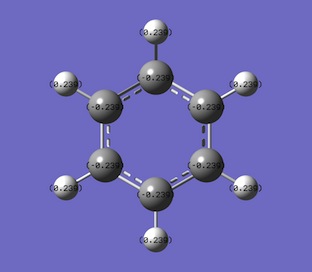
Table below outlines the charge distribution in the optimised benzene molecule.
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
C 1 -0.23854 1.99910 4.22613 0.01331 6.23854
C 2 -0.23854 1.99910 4.22613 0.01331 6.23854
C 3 -0.23854 1.99910 4.22613 0.01331 6.23854
C 4 -0.23854 1.99910 4.22613 0.01331 6.23854
C 5 -0.23854 1.99910 4.22613 0.01331 6.23854
C 6 -0.23854 1.99910 4.22613 0.01331 6.23854
H 7 0.23854 0.00000 0.76002 0.00144 0.76146
H 8 0.23854 0.00000 0.76002 0.00144 0.76146
H 9 0.23854 0.00000 0.76002 0.00144 0.76146
H 10 0.23854 0.00000 0.76002 0.00144 0.76146
H 11 0.23854 0.00000 0.76002 0.00144 0.76146
H 12 0.23854 0.00000 0.76002 0.00144 0.76146
=======================================================================
* Total * 0.00000 11.99462 29.91691 0.08846 42.00000
Hybridisation:
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.98097) BD ( 1) C 1 - C 2
( 50.00%) 0.7071* C 1 s( 35.20%)p 1.84( 64.76%)d 0.00( 0.04%)
-0.0001 0.5932 -0.0079 0.0006 -0.7063
-0.0300 -0.3840 0.0193 0.0000 0.0000
0.0151 0.0000 0.0000 0.0069 -0.0109
( 50.00%) 0.7071* C 2 s( 35.20%)p 1.84( 64.76%)d 0.00( 0.04%)
-0.0001 0.5932 -0.0079 0.0006 0.6857
-0.0017 0.4197 0.0357 0.0000 0.0000
0.0135 0.0000 0.0000 0.0096 -0.0109
4. (1.98305) BD ( 1) C 1 - H 7
( 62.04%) 0.7876* C 1 s( 29.58%)p 2.38( 70.39%)d 0.00( 0.04%)
-0.0003 0.5437 0.0126 -0.0010 0.0000
0.0000 0.8388 -0.0146 0.0000 0.0000
0.0000 0.0000 0.0000 -0.0166 -0.0105
( 37.96%) 0.6161* H 7 s( 99.95%)p 0.00( 0.05%)
0.9997 0.0014 0.0000 -0.0228 0.0000
Above in the calculated hybridizations of the C-C, and C-H bonds.
Table below summarises information in a clearer presentation.
| Nature of Bond | Hybridization |
|---|---|
| C 50% C50% | Carbon 35.20% 1s, 64.76% p |
| C 62.04% H 35.96 | Carbon 29.58%s 70.39%p; Hydrogen 99.95%s |
Results above are what is expected;
Each carbon atom has the expect hybridisation of sp2 with aromatic pi electron density. In C-C bonds, theres equal contribution of the carbon atoms, as benzene is symmetry and each carbon are equivalent electronically.
Boratabenzene
Boratabenzene is an analogue of benzene where one C-H unit id replaced with a B-H unit.
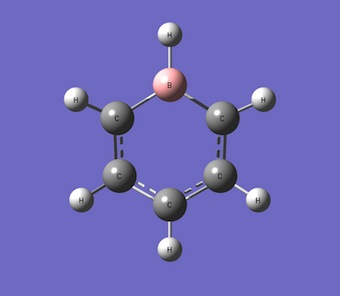
Optimisation
Item Value Threshold Converged? Maximum Force 0.000286 0.000450 YES RMS Force 0.000110 0.000300 YES Maximum Displacement 0.001525 0.001800 YES RMS Displacement 0.000453 0.001200 YES Predicted change in Energy=-1.088644D-06 Optimization completed.
The table above shows that the 6-31G (d,p) optimisation was successful with both the force and displacements converging.
| File Name | boratabenzene_Opt |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Charge | -1 |
| Spin | Singlet |
| E(RB3LYP) | -219.02053046 a.u. |
| RMS Gradient Norm | 0.00003126 a.u. |
| Imaginary Freq | |
| Dipole Moment | 2.8449 Debye |
| Point Group | C1 |
Bond Distance:
B-C bond: 1.51133 Â
B-H bond: 1.21723 Â
C(5/4)-C(1/3) bond: 1.39681 Â
C(1/3)-C(2) bond: 1.40284 Â
C-H bond: 1.09421 Â
Frequency
Low frequencies --- -7.8764 0.0002 0.0003 0.0005 9.2958 9.7791
Low frequencies --- 371.4522 404.1650 565.1770
Top row frequencies are all within 15 cm-1 of each other, and are an order of magnitude of the second row frequencies. This shows frequency calculation where correctly done.
| File Name | Boratabenzene_FREQ |
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Charge | -1 |
| Spin | Singlet |
| E(RB3LYP) | -219.02053046 a.u. |
| RMS Gradient Norm | 0.00003121 a.u. |
| Imaginary Freq | |
| Dipole Moment | 2.8449 Debye |
| Point Group | C1 |
Molecular Orbital Analysis
Natural Bond Analysis
Natural bond orbital analysis [NBO] was computed form the optimised boratabenzene molecule.
The charge range for the NBO charge distribution was -0.588 to +0.588
| Atom | Charge |
|---|---|
| B | 0.202 |
| C(1/2/3) | -0.588/-0.250/-0.340 |
| H(B-H/C1-H/C2-H/C3-H) | -0.097/0.184/0.179/0.186 |
Below is computed charge distribution of the optimised Boratabenzene
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
C 1 -0.25034 1.99910 4.23711 0.01413 6.25034
C 2 -0.34000 1.99907 4.32709 0.01384 6.34000
C 3 -0.25034 1.99910 4.23711 0.01413 6.25034
C 4 -0.58808 1.99901 4.57728 0.01178 6.58808
C 5 -0.58808 1.99901 4.57728 0.01178 6.58808
H 6 0.17899 0.00000 0.81838 0.00263 0.82101
H 7 0.18573 0.00000 0.81228 0.00199 0.81427
H 8 0.17899 0.00000 0.81838 0.00263 0.82101
H 9 0.18387 0.00000 0.81395 0.00218 0.81613
H 10 -0.09652 0.00000 1.09598 0.00054 1.09652
H 11 0.18387 0.00000 0.81395 0.00218 0.81613
B 12 0.20190 1.99906 2.78743 0.01160 4.79810
=======================================================================
* Total * -1.00000 11.99436 29.91623 0.08941 42.00000
Below contains a table, that has the orbital percentage of contribution to each hybridisation.
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.97969) BD ( 1) C 1 - C 2
( 49.96%) 0.7068* C 1 s( 35.53%)p 1.81( 64.44%)d 0.00( 0.04%)
-0.0001 0.5960 -0.0075 0.0006 0.6873
0.0034 0.4134 0.0325 0.0000 0.0000
0.0146 0.0000 0.0000 0.0080 -0.0107
( 50.04%) 0.7074* C 2 s( 35.87%)p 1.79( 64.09%)d 0.00( 0.04%)
-0.0001 0.5989 -0.0072 0.0010 -0.7062
-0.0327 -0.3754 0.0141 0.0000 0.0000
0.0137 0.0000 0.0000 0.0078 -0.0107
( 40.68%) 0.6378* H 6 s( 99.95%)p 0.00( 0.05%)
-0.9998 -0.0026 -0.0187 0.0116 0.000
4. (1.98568) BD ( 1) C 1 - H 6
( 59.32%) 0.7702* C 1 s( 26.85%)p 2.72( 73.10%)d 0.00( 0.05%)
0.0003 -0.5180 -0.0134 0.0012 0.7229
-0.0089 -0.4563 0.0100 0.0000 0.0000
0.0177 0.0000 0.0000 -0.0070 0.0111
11. (1.96997) BD ( 1) C 4 - B 12
( 66.70%) 0.8167* C 4 s( 41.99%)p 1.38( 58.00%)d 0.00( 0.01%)
0.0000 -0.6478 -0.0159 -0.0012 0.6119
-0.0293 0.4524 0.0090 0.0000 0.0000
-0.0059 0.0000 0.0000 -0.0041 0.0057
( 33.30%) 0.5770* B 12 s( 33.40%)p 1.99( 66.52%)d 0.00( 0.08%)
0.0000 -0.5779 0.0059 -0.0048 -0.7056
-0.0394 -0.4070 0.0096 0.0000 0.0000
-0.0230 0.0000 0.0000 -0.0082 0.0133
14. (1.98608) BD ( 1) H 10 - B 12
( 55.09%) 0.7422* H 10 s( 99.97%)p 0.00( 0.03%)
0.9998 0.0001 0.0000 0.0180 0.0000
( 44.91%) 0.6701* B 12 s( 33.16%)p 2.01( 66.78%)d 0.00( 0.06%)
-0.0005 0.5758 0.0069 -0.0060 0.0000
0.0000 -0.8172 0.0016 0.0000 0.0000
0.0000 0.0000 0.0000 -0.0213 -0.0105
Table below summarises information in a clearer presentation.
| Nature of Bond | Hybridization |
|---|---|
| C 49.96% C 50.04% | Carbon 35.53% 1s, 64.44% p |
| C 9.32% H 40.68% | Carbon 26.85%1s, 73.10%p; Hydrogen 99.95%s |
| B 33.30% C 66.70% | Carbon 41.99%s, 58.00%p; Boron 33.40%s, 66.52%p |
| B 44.91% H 55.09% | Boron 33.16%s, 66.78%p; Hydrogen 99.97%s |
All C-C bonds are sp2 hybrid as you can see from the ratio between the s:p orbitals. Whereas B-C, carbon has a greater s character hybridisation is more sp then sp2, this is because boron has a more electron density (due to negative charge) compared to carbon atoms, therefore electron density is 'dumped' into carbon s orbital, increasing its contribution in hybridisation. Boron has a sp2 hybridisation as shown from there relative s:p orbital contributions.
Pyridinium
Pyridinum is another analogue of benzene where a C-H unit from benzene, is replaced by a N+-H unit.
Optimisation
File:Pyridinium optimisation.log
0.00003 0.00000 0.00000 -0.00003 -0.00003 0.00000
Item Value Threshold Converged?
Maximum Force 0.000065 0.000450 YES
RMS Force 0.000023 0.000300 YES
Maximum Displacement 0.000627 0.001800 YES
RMS Displacement 0.000160 0.001200 YES
Predicted change in Energy=-6.498357D-08
Optimization completed.
The table above shows that the 6-31G (d,p) optimisation was successful with both the force and displacements converging.
| File Name | Pyridinium_OPT |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Charge | 1 |
| Spin | Singlet |
| E(RB3LYP) | -248.66807396 a.u. |
| RMS Gradient Norm | 0.00003894 a.u. |
| Imaginary Freq | |
| Dipole Moment | 1.8727 Debye |
| Point Group | C1 |
Bond Distances:
N-C= 1.35237 Â
N-H= 1.01692 Â
C-C= 1.38286 Â
C-C= 1.39876
C(4/5)-H= 1.08324 Â
C(1/3)-H= 1.08324 Â
C(2)-H= 1.08520 Â
Frequency
Full mass-weighted force constant matrix: Low frequencies --- -7.2196 -0.0009 -0.0006 0.0001 0.0007 3.3584 Low frequencies --- 392.4574 404.0611 620.4719
Top row frequencies are all within 15 cm-1 of each other, and are an order of magnitude of the second row frequencies. This shows frequency calculation where correctly done.
Molecular Orbital analysis
| Occupied molecular orbitals of Pyridinium | ||||
|---|---|---|---|---|
 |
 |
 |
 |

|
 |
 |
 |
 |

|
 |
 |
 |
 |

|
 |
 |
 |
 |

|
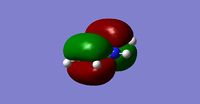
| ||||
Natural Bond Analysis

Natural bond orbital analysis [NBO] was computed form the optimised pyridinum molecule.
The charge range for the NBO charge distribution was -1.000 to +1.000
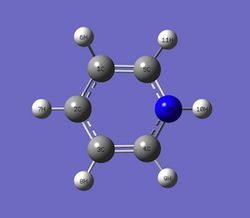
| Atom | Charge |
|---|---|
| H(10) | 0.483 |
| H(11/9) | 0.285 |
| H(5/8) | 0.297 |
| H(7) | 0.292 |
| C(5/4) | 0.071 |
| C(1/3) | -0.241 |
| C(2) | -0.122 |
| N(12) | -0.475 |
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
C 1 -0.24103 1.99912 4.22860 0.01331 6.24103
C 2 -0.12241 1.99913 4.10941 0.01386 6.12241
C 3 -0.24104 1.99912 4.22860 0.01331 6.24104
C 4 0.07100 1.99918 3.91066 0.01916 5.92900
C 5 0.07098 1.99918 3.91068 0.01916 5.92902
H 6 0.29719 0.00000 0.70179 0.00103 0.70281
H 7 0.29170 0.00000 0.70718 0.00113 0.70830
H 8 0.29718 0.00000 0.70179 0.00103 0.70282
H 9 0.28493 0.00000 0.71397 0.00110 0.71507
H 10 0.48279 0.00000 0.51475 0.00246 0.51721
H 11 0.28493 0.00000 0.71397 0.00110 0.71507
N 12 -0.47622 1.99937 5.46756 0.00929 7.47622
=======================================================================
* Total * 1.00000 11.99510 29.90895 0.09595 42.00000
Hybridisation:
Below contains a table, that has the orbital percentage of contribution to each hybridisation.
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.98249) BD ( 1) C 1 - C 2
( 50.26%) 0.7089* C 1 s( 34.73%)p 1.88( 65.23%)d 0.00( 0.04%)
0.0000 0.5893 -0.0066 0.0009 -0.4185
-0.0371 -0.6897 0.0068 0.0000 0.0000
0.0122 0.0000 0.0000 -0.0118 -0.0115
( 49.74%) 0.7053* C 2 s( 34.45%)p 1.90( 65.51%)d 0.00( 0.04%)
0.0000 0.5869 -0.0086 0.0005 0.3935
-0.0234 0.7063 0.0290 0.0000 0.0000
4. (1.97822) BD ( 1) C 1 - H 6
( 64.83%) 0.8052* C 1 s( 31.78%)p 2.15( 68.19%)d 0.00( 0.03%)
-0.0003 0.5636 0.0138 -0.0005 -0.3988
0.0072 0.7229 -0.0181 0.0000 0.0000
-0.0109 0.0000 0.0000 -0.0085 -0.0099
( 35.17%) 0.5930* H 6 s( 99.94%)p 0.00( 0.06%)
0.9997 0.0016 0.0116 -0.0208 0.0000
11. (1.98861) BD ( 1) C 4 - N 12
( 36.68%) 0.6057* C 4 s( 28.13%)p 2.55( 71.74%)d 0.00( 0.13%)
-0.0001 0.5293 -0.0335 -0.0013 0.4043
0.0563 0.7416 0.0277 0.0000 0.0000
0.0252 0.0000 0.0000 -0.0185 -0.0179
( 63.32%) 0.7957* N 12 s( 36.56%)p 1.73( 63.41%)d 0.00( 0.03%)
-0.0001 0.6047 -0.0037 0.0006 -0.3660
0.0187 -0.7069 -0.0132 0.0000 0.0000
0.0107 0.0000 0.0000 -0.0059 -0.0115
15. (1.98630) BD ( 1) H 10 - N 12
( 25.41%) 0.5041* H 10 s( 99.88%)p 0.00( 0.12%)
0.9994 -0.0064 -0.0342 0.0000 0.0000
( 74.59%) 0.8637* N 12 s( 26.82%)p 2.73( 73.16%)d 0.00( 0.02%)
-0.0002 0.5178 0.0066 -0.0013 0.8553
-0.0091 -0.0001 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0115 -0.0106
Table below summarises information in a clearer presentation.
| Nature of Bond | Hybridization |
|---|---|
| C49.74% C 50.26% | Carbon 34.73% s, 65.23% p |
| C59.32% H 40.68% | Carbon 31.78% s, 68.19% p; Hydrogen 99.95%s |
| N63.32% C 36.68% | Carbon 28.13%s, 71.74p; Nitrogen 36.56% s, 63.41% p |
| N 74.59% H 25.41% | Nitrogen 26.82% s, 73.16% p; Hydrogen 99.88%s |
Borazine
Optimisation
Item Value Threshold Converged? Maximum Force 0.000093 0.000450 YES RMS Force 0.000033 0.000300 YES Maximum Displacement 0.000301 0.001800 YES RMS Displacement 0.000092 0.001200 YES Predicted change in Energy=-1.020701D-07 Optimization completed.
The above shows that the 6-31G (d,p) optimisation was successful with both the force and displacements converging
| File Name | Borazine_OPT |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -242.68458751 a.u. |
| RMS Gradient Norm | 0.00009009 a.u. |
| Imaginary Freq | |
| Dipole Moment | 0.00006595 Debye |
| Point Group | C1 |
Bond Distance:
B-N= 1.43064 Â N-H= 1.00973 Â
B-H= 1.19494 Â
Frequency
Low frequencies --- -8.9527 -6.3045 -0.0009 -0.0004 0.0011 4.1115 Low frequencies --- 288.8362 289.6995 404.1678
Top row frequencies are all within 15 cm-1 of each other, and are an order of magnitude of the second row frequencies. This shows frequency calculation where correctly done.
| File Name | Borazine_FREQ |
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -242.68458743 a.u. |
| RMS Gradient Norm | 0.00006597 a.u. |
| Imaginary Freq | |
| Dipole Moment | 0.0002 Debye |
| Point Group | C1 |
Molecular Orbital Analysis
| Occupied molecular orbitals of Borazine | ||||
|---|---|---|---|---|
 |
 |
 |
 |

|
 |
 |
 |
 |

|
 |
 |
 |
 |

|
 |
 |
 |
 |
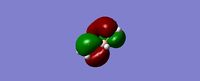
|

| ||||
Natural Bond Analysis

Natural bond orbital analysis [NBO] was computed form the optimised borazine molecule.
The charge range for the NBO charge distribution was -1.000 to +1.000
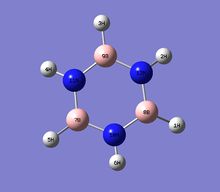
| Atom | Charge |
|---|---|
| B | 0.747 |
| N | -1.02 |
| H(N-H/B-H) | 0.432/-0.077 |
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
H 1 -0.07654 0.00000 1.07585 0.00069 1.07654
H 2 0.43199 0.00000 0.56573 0.00228 0.56801
H 3 -0.07655 0.00000 1.07586 0.00069 1.07655
H 4 0.43198 0.00000 0.56574 0.00228 0.56802
H 5 -0.07654 0.00000 1.07585 0.00069 1.07654
H 6 0.43198 0.00000 0.56574 0.00228 0.56802
B 7 0.74700 1.99917 2.23862 0.01520 4.25300
B 8 0.74695 1.99917 2.23868 0.01521 4.25305
B 9 0.74696 1.99917 2.23866 0.01521 4.25304
N 10 -1.10241 1.99943 6.09821 0.00478 8.10241
N 11 -1.10241 1.99943 6.09820 0.00478 8.10241
N 12 -1.10240 1.99943 6.09819 0.00478 8.10240
=======================================================================
* Total * 0.00000 11.99579 29.93532 0.06889 42.00000
Hybridisation
(Occupancy) Bond orbital/ Coefficients/ Hybrids ---------------------------------------------------------------------------------
5. (1.98670) BD ( 1) H 5 - B 7
( 54.03%) 0.7351* H 5 s( 99.96%)p 0.00( 0.04%)
0.9998 0.0002 0.0154 0.0114 0.0000
( 45.97%) 0.6780* B 7 s( 37.48%)p 1.67( 62.46%)d 0.00( 0.07%)
-0.0006 0.6120 0.0129 -0.0016 -0.6356
0.0216 -0.4689 0.0160 0.0000 0.0000
0.0226 0.0000 0.0000 0.0070 -0.0098
6. (1.98495) BD ( 1) H 6 - N 10
( 28.08%) 0.5299* H 6 s( 99.91%)p 0.00( 0.09%)
-0.9996 0.0010 0.0033 -0.0293 0.0000
( 71.92%) 0.8481* N 10 s( 22.82%)p 3.38( 77.15%)d 0.00( 0.03%)
0.0002 -0.4776 0.0114 -0.0006 -0.0981
-0.0015 0.8728 0.0130 0.0000 0.0000
0.0027 0.0000 0.0000 0.0119 0.0119
7. (1.98438) BD ( 1) B 7 - N 10
( 23.53%) 0.4851* B 7 s( 31.25%)p 2.19( 68.50%)d 0.01( 0.25%)
0.0003 -0.5587 0.0174 -0.0032 -0.7654
-0.0271 0.3096 0.0510 0.0000 0.0000
0.0290 0.0000 0.0000 -0.0347 0.0206
( 76.47%) 0.8745* N 10 s( 38.55%)p 1.59( 61.44%)d 0.00( 0.01%)
0.0000 -0.6209 -0.0043 0.0001 0.7404
-0.0019 -0.2567 0.0158 0.0000 0.0000
0.0046 0.0000 0.0000 -0.0055 0.0085
Table below summarises information in a clearer presentation.
| Nature of Bond | Hybridization |
|---|---|
| N76.47% B 23.53% | Nitrogen 38.55 s, 61.55% p; 37.48%s, 62.46%p |
| B45.97% H 54.03% | Boron 37.48%s, 62.46%p; Hydrogen 100.00%s |
| N71.92 H 28.08% | Nitrogen 22.82%s, 77.15%p; Hydrogen 100.00%s |
The table above shows that Boron has a sp2 hybridization, Nitrogen has a bigger bonding coefficient in both its bonds, this is due to its greater electronegative nature compared to Boron and Hydrogen. In contrast Boron has the smaller bonding coefficient in both its bonds, this is due to its electropossitive nature.
Analysis of benzene and its analogues
Comparing Charge Distribution
| Charge distribution analysis | |||
|---|---|---|---|
| Benzene | Boratabenzene | Pyridinium | Borazine |
 |
 |
 |

|
 |
 |
 |
|
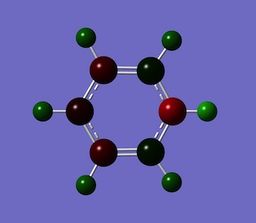
Benzene contains 6 electronically equivalent carbons, and has a symmetry of D6H. Its expected and shown that benzene has a equal charge distribution over all the carbon atoms, and therefore all the hydrogens have the same charge distribution. each carbon contains a charge of -0.239 and each hydrogen a charge of +0.239. Carbon has a negative charge as its more electronegative with respect to hydrogen.
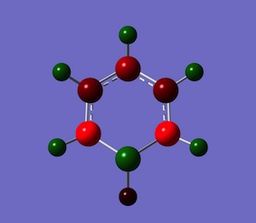
Boratabenzene, an analogue of benzene whereby a C-H unit is replaced with a B-H unit. The Boron atom in Boratabenzene contains a negative charge within its pz orbitals, perpendicular to the ring. The negative charge means Boratabenzene is isoelectric with benzene, but even though its isoelelectric with bezene is charge distribution is some what different. the boron atom contains a charge of +0.202, and the hydrogen bonded to the boron has a charge of -0.097, this shows the effect boron has, as its formally an electropositive atom, with respect to hydrogen, it contains a positive charge distribution. In boratabenzene the charge is polarised towards the ortho carbon. The ortho carbon has a greater share of electron density, and it is reflected by its charge with respect to meta and para carbons. Ortho= -0.588, Meta= -0.250, Para= -0.340.
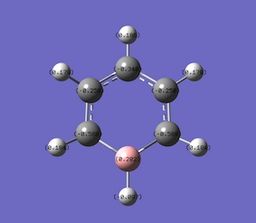
Pyridinum contains a N-H unit that replaces a C0H unit in benzene. the nitrogen atom contains a positive charge, therefore isoelectric with benzene. The nitrogen has a charge of -0.476 and the hydrogen bonded to the nitrogen has a charge of +0.438, Nitrogen is electronegtive with respect to hydrogen so will 'hold' a greater share of electron density in the N-H bond. Nitrogen disrupts the charge distribution due to its high electronegative nature, where inductive effect causes ortho carbons have a charge distribution of +0.071, relatively positive, no positive carbon is observed in benzene and Boratabenzene.
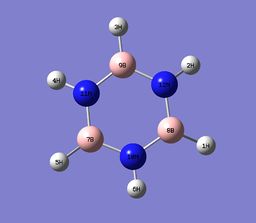
Borazine is a siz-memberred ring that contains alternating B-H and N0H units, this forms a symmetric distribution of charge. nitrogen is more electronegative with respect to boron and boron is more electropositive with respect to nitrogen. This means Boron is more 'happy' to let nitrogen have a greater share of its electrons, and Nitrogen wants to pull electron density towards itself more than boron. This in a sense is a 'double. affect and its observed but Nitrogen contains a greater charge distribution of -1.102, then the nitrogen in pydrinum (-0.476) and boron contins a greater positive charge in borazine of +0.747 then it does in boratabenzene (+0.202). The hydrogen atoms bonded to Nitrogen contain a charge of +0.432 and the hydrogens bonded to boron contain a charge of -0.077, due to the electropositive nature of boron.
Comparing Molecular Orbitals:
The HOMO, HOMO-1 and the pi-system orbitals where compared with respect to benzene. As each molecule was optimisation using the same method and basis set, difference in the orbitals are due to the molecules quantum mechanics.
| HOMO Molecular orbitals | ||||
|---|---|---|---|---|
| Molecule | Benzene | Boratabenzene | Pyridinium | Borazine |
| HOMO |  |
 |
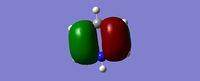 |

|
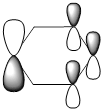
| LCAOs | 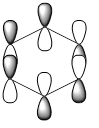 |
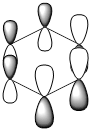 |
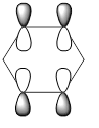 |
|
| Energy (a.u) | -0.2469 | +0.01096 | -0.47885 | -0.27590 |
The HOMO of benzene contains a nodal plane across to the ring system, it has equal charge distribution across each node. Boratabenzene is overall negatively charged (on the boron) this causes an asymmetric perturbation in the pi cloud, therefore a greater electron density is present around the boron and causes nodal planes each side of the boron. Pyridinum has a nodal plane through the ring by the nitrogen atom and para carbon atom, with no electron density around the nitrogen, this is mainly due to the positive charge on the nitrogen atom. borazine has a nodal plane, perpendicular to the B-N ring system, Given the disparity in the electronegativities between boron and nitrogen, there is a slight distortion in the electron density towards the nitrogen atom that lies along the nodal plane.
| HOMO-1 Molecular orbitals | ||||
|---|---|---|---|---|
| Molecule | Benzene | Boratabenzene | Pyridinium | Borazine |
| HOMO-1 |  |
 |
 |

|
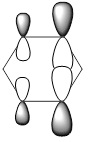
| LCAOs | 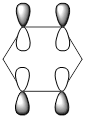 |
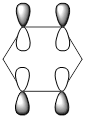 |
 |
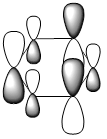
|
| Energy (a.u) | -0.24692 | -0.03483 | -0.50847 | -0.27589 |
| pi-system Molecular orbitals | ||||
|---|---|---|---|---|
| Molecule | Benzene | Boratabenzene | Pyridinium | Borazine |
| pi-system |  |
 |
 |

|
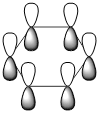
| LCAOs | 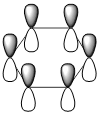 |
 |
 |
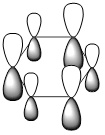
|
| Energy (a.u) | -0.2469 | +0.01096 | -0.47885 | -0.27590 |
Each molecule exhibits a isonodal molecular orbitals, where the only nodal plane present is through the ring system. This means theres a no electron density across the ring system and with a full pi-system above and below each ring system. Using benzene as a reference to its analogues (because it has equal electron density across each phase, due to its D3h symmetry) we will compare and contrast its analogues.
Boratabenzene molecular orbital and LCAO, look almost exactly the same as benzene. This is due to the negative charge located in its 2pz orbital, which in-turn can contribute to the pi system (near) equal as the other carbons, very little perturbation due to electropositive nature of boron. Also good overlap between Boron and carbon, 2pz orbitals. For pyridinum,as shown in the MO and LCAO the p orbital on nitrogen contributes a much greater electron density, causing polarisation in electron density and breaking its symmetry. Borazine consist of alternating Boron and Nitrogen atoms (intern alternating electropositive and electronegative atoms, respectively) therefore the differences in electronegtivety cancel out across the system forming even electron density across the syste.
Energies of the molecular orbitals, depend on the atomic orbitals in the system, therefore as observed systems containing electronegative (in this case only nitrogen) experience a lower energy. Hence why pyridinum has the lowest energy as observed, despite Borazine containing three nitrogen atoms, its electronegativety is somehwat levels outs due to the alternating boron atoms. Conversely, Boratabenzene has the highest energy.