Rep:Mod:yf04q1
Introduction
Optimisation of Trigonal Planar Molecules
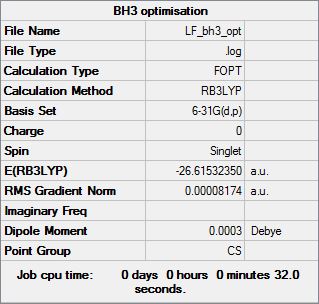
BH3 Optimisation
The software used for the optimisations was GuassView v5. For the BH3 two different optimisations where done. The 1st was quick less accurate calculation with D3h symmetry was imposed (GuassView assumes CS symmetry), The Calculation Method was RB3LYP and Basis set was 3-21G. Below the optimisation results is summerised:
| File name | BH3_OTP | cell |
| File Type | .log | |
| Calculation type | FOPT | |
| Calculation Method | RB3LYP | |
| Basis Set | 3-21G | |
| Charge | 0 | |
| Spin | Singlet | |
| E(RB3LYP) | -26.61532289 | a.u. |
| RMS Gradient Norm | 0.00004507 | a.u. |
| Imaginary Freq | ||
| Dipole Moment | 0.000 | Debye |
| Point Group | D3H |
Item Value Threshold Converged? Maximum Force 0.000090 0.000450 YES RMS Force 0.000059 0.000300 YES Maximum Displacement 0.000360 0.001800 YES RMS Displacement 0.000235 0.001200 YES Predicted change in Energy=-4.861204D-08 Optimization completed.
The information box above, method and basis calculations where imposed and optimisation was successfully complete.
| Bond type | Bond Length  |
|---|---|
| B-H(1) | 1.19453 |
| B-H(2) | 1.19453 |
| B-H(3) | 1.19453 |
| Bond type | Bond angle ° |
|---|---|
| H(2)-B-H(1) | 120.00 |
| H(H3_B-H(2) | 120.00 |
| (1)B-H(3) | 120.00 |
Improved 'Basis Set' to 6-31G(d,p)
The second optimisation consisted with a D3h symmetry imposed onto the molecule along with a more accurate basis set of 6-31G. Below the optimisation results is summerised:
| File name | YF_BH3_OPT_631g | cell |
| File Type | .log | |
| Calculation type | FOPT | |
| Calculation Method | RB3LYP | |
| Basis Set | 6-31G(d,p) | |
| Charge | 0 | |
| Spin | Singlet | |
| E(RB3LYP) | - 26.61532321 | a.u. |
| RMS Gradient Norm | 0.00020295 | a.u. |
| Imaginary Freq | ||
| Dipole Moment | 0.0016 | Debye |
| Point Group | D3H |
Item Value Threshold Converged? Maximum Force 0.000355 0.000450 YES RMS Force 0.000232 0.000300 YES Maximum Displacement 0.001408 0.001800 YES RMS Displacement 0.000922 0.001200 YES Predicted change in Energy=-7.487453D-07 Optimization completed.
The information box above, method and basis calculations where imposed and optimisation was successfully complete.

| Bond type | Bond Length  |
|---|---|
| B-H(1) | 1.9307 |
| B-H(2) | 1.9307 |
| B-H(3) | 1.9307 |
| Bond type | Bond angle ° |
|---|---|
| H(2)-B-H(1) | 120.00 |
| H(H3_B-H(2) | 120.00 |
| (1)B-H(3) | 120.00 |
As expected for a D3h symmetry to be imposed all B-H bond distances must be equal, and H-B-H bond angels to be 120°. As well as no dipole moment.
BBr3 Optimisation
| File name | log_86081 BBR3 HPC | |
| File Type | .log | |
| Calculation type | FOPT | |
| Calculation Method | RB3LYP | |
| Basis Set | Gen | |
| Charge | 0 | |
| Spin | Singlet | |
| E(RB3LYP) | -64.43644624 a.u. | |
| RMS Gradient Norm | 0.00001068 a.u. | |
| Imaginary Freq | ||
| Dipole Moment | 0.0002 | Debye |
| Point Group | CS |
Item Value Threshold Converged? Maximum Force 0.000019 0.000450 YES RMS Force 0.000011 0.000300 YES Maximum Displacement 0.000078 0.001800 YES RMS Displacement 0.000053 0.001200 YES Predicted change in Energy=-1.966661D-09 Optimization completed.
The information box above, method and basis calculations where imposed and optimisation was successfully complete.
| Bond type | Bond Length  |
|---|---|
| B-Br(4) | 1.93392 |
| B-Br(2) | 1.93398 |
| B-Br(3) | 1.93400 |
| Bond type | Bond angle ° |
|---|---|
| Br(2)-B-Br(3) | 120.001 |
| Br(3)-B-Br(4) | 120.006 |
| Br(4)-B-Br(2) | 119.093 |
GaBr3 Optimisation
GaBr3 is a very electronic rich molecule owing to the 35 electrons on each Br atom [Electron configuration: 1s22s22p63s23p64s23d104p5]. Both atoms exhibit relativistic effects which can't be recovered using the standard Schrödinger equation. Therefore a pseudo-potential is used, this assumes valence electrons dominates in bonding interactions. By using the LanL2DZ basis set, the program uses a medium level basis set: D95V on first row atoms and Los Alamos ECP on heavier atoms. Molecule was restricted to a D3H symmetry.
| File name | GABR3_OTP_HPC | |
| File Type | .log | |
| Calculation type | FOPT | |
| Calculation Method | RB3LYP | |
| Basis Set | LANL2DZ | |
| Charge | 0 | |
| Spin | Singlet | |
| E(RB3LYP) | -41.70082783 a.u. | |
| RMS Gradient Norm | 0.00000016 a.u. | |
| Imaginary Freq | ||
| Dipole Moment | 0.0000 | Debye |
| Point Group | D3H |
Item Value Threshold Converged? Maximum Force 0.008057 0.000450 YES RMS Force 0.005274 0.000300 YES Maximum Displacement 0.071167 0.001800 YES RMS Displacement 0.046590 0.001200 YES Predicted change in Energy=-8.731494D-04
Optimization complete.
| Bond type | Bond Length  |
|---|---|
| Ga-Br(4) | 2.35 |
| Ga-Br(2) | 2.35 |
| Ga-Br(3) | 2.35 |
| Bond type | Bond angle ° |
|---|---|
| Br(2)-Ga-Br(3) | 120.00 |
| Br(3)-Ga-Br(4) | 120.00 |
| Br(4)-Ga-Br(2) | 119.00 |
Bond length analysis
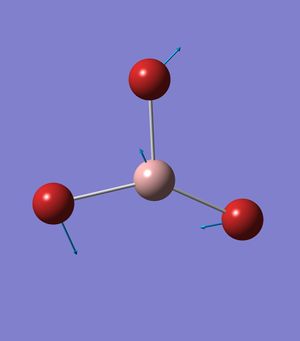
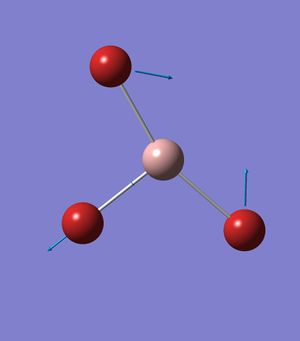
Vibrational analysis of trigonal planar molecules
BH3
Full mass-weighted force constant matrix:
Low frequencies --- -16.5502 -0.0006 0.0008 0.0009 36.8499 50.6128
Low frequencies --- 1163.4259 1212.8178 1214.1503
Initial calculations of the BH3 frequency, the low frequencies corresponding to the boron centre was not with ±15cm-1. So frequency calculations where not acceptable to carry out further analysis. The mole was created again and optimised again and recalcuulted with 'Job Type' changed to frequency.
Low frequencies --- -0.1687 -0.0769 -0.0053 5.7455 11.7246 11.7625
Low frequencies --- 1164.3334 1214.0826 1214.0853
These frequencies are due to the motions of the center of mass of the molecule and are within an acceptable range of +/- 15 cm-1. They are an order of magnitude smaller than the "real" frequencies [which are always positive] found on the second line.
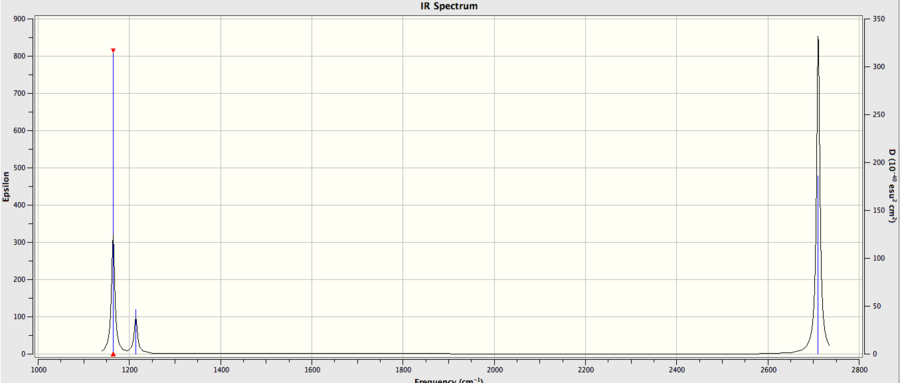
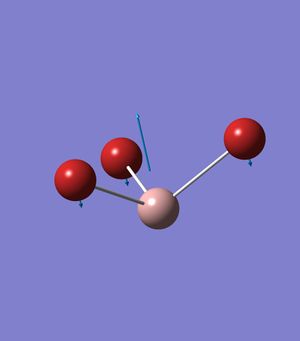
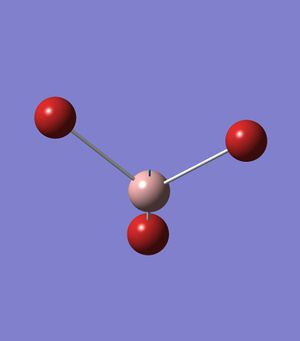
GaBr3
Low frequencies --- -0.5252 -0.5247 -0.0024 -0.0010 0.0235 1.2010
Low frequencies --- 76.3744 76.3753 99.6982
frequencies are due to the motions of the center of mass of the molecule and are within an acceptable range of +/- 15 cm, and are a magnitude smaller then the second row of frequencies.
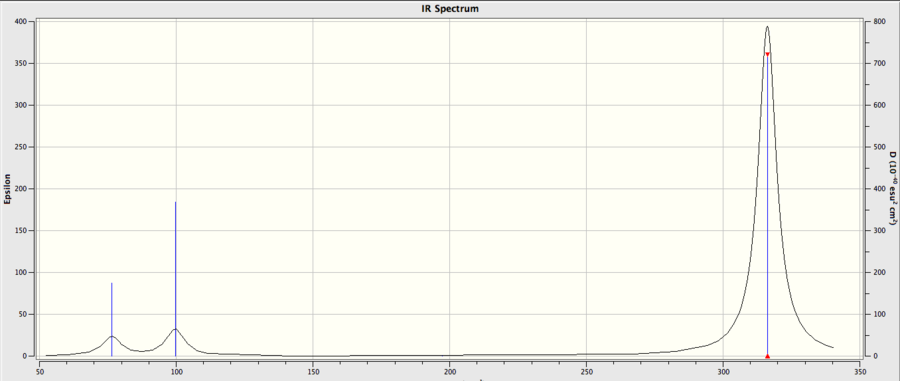
Only 3 peaks are shown out the the 6 vibrational modes calculated,
BH3 and GaBr3 frequency comparison
| Motion | BH3 Frequency | GaBr3 frequency |
|---|---|---|
| 1 | 1166.33 | 76.37 |
| 2 | 1214.08 | 76.36 |
| 3 | 1214.09 | 368.78 |
| 4 | 2577.60 | 00.00 |
| 5 | 2710.32 | 720.08 |
| 6 | 2710.32 | 720.12 |
Clearly, from the table BH3 appears to have significantly higher vibrational frequencies in comparison to GaBr3. The frequency is proportional to the bond strength, where the stronger the bond, the higher the frequency and vice versa. This is in accordance with the harmonic oscillator approximation, derived from Hooke’s Law, which states that the deviation od a system from its equilibrium position is proportional to the restoring force, F=-kx ([where F is the restoring force, k is a positive force constant and x is the displacement in cm’s). Vibrational energy levels within the harmonic oscillator are calculated as E= (v+1/2) ħω with the frequency, ω, defined as ω = (kf/μ)½ (μ is the reduced mass given by m1m2/m1+m2). Now it is clear that frequency is inversely proportional to the reduced mass, the larger the overall mass of the two atoms the smaller the vibrational frequency.
H+Br = 1+79.99=80.99 u and Ga+Br= 69.72+79.99= 149.71 u
Ga-Br bond results in a smaller frequency, with respect to the H-Br bond.
Both BH3 and GaBr3 both possess six vibrational frequencies, as they are isostructural. Despite having the same symmetries within both molecules, there vibrational mode frequencies order are different. The ascening frequency order for BH3 is A2', E1', E1', A1, E1', E1' and for GaBr3 the ascending order is E1', E1',A2',A1,E1',E1'.
Vibrations are categorised into stretching or bending modes (i.e rocking, scissoring, wagging and twisting). The frequency at stretching occurs (strength the bond, with energy defined as E=hw) is higher than of corresponding bending. Hence, for both isostructrual molecules the bending moles appear on the far left hand on the spectra (lower energy modes), which the stretching modes appear on the right side of the spectra (higher energy modes)
The A2' mode in GaBr3 is higher in energy compared to the E1' mode, and in BH3 the opposite is observed. compared to BH3 due to the heavier Br atoms with need more energy to bending the atoms in and out the plane, compared to BH3, where H is much lighter therefore less energy is needed, hence less energetic. The lower E1' modes in both molecule exhibit the same vibrational motions (rocking, scissoring and bending).
Lastly, its observed in both spectrums only 3 peaks are observed, despite having 6 vibrations. The degeneracy of of the lower and higher E1‘ modes, results in two sets of vibrational frequencies overlapping, so only four peaks would be expected. But only 3 is observed, this can be explained but basic Infrared Spectrum theory where the 4th mode in both molecules results in a totally symmetric motion, resulting in no dipole moment, modes are ‘IR inactive’, hence why no peak is observed.
Molecular Orbital
| File name | YF_BH3_NBOS |
| File Type | .log |
| Calculation type | SP |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -26.61532288 a.u. |
| RMS Gradient Norm | |
| Imaginary Freq | |
| Dipole Moment | 0.000 Debye |
| Point Group | D3H |
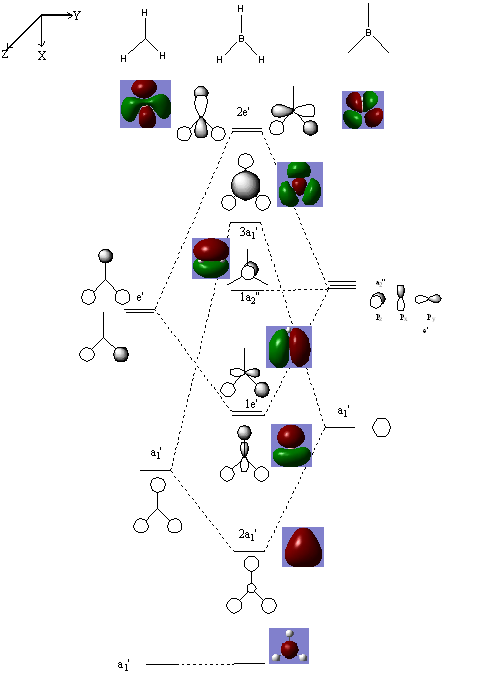
Molecular orbital Diagram
Below is the molecular orbital diagram showing the mixing of orbitals of the same symmetry, between orbitals on the boron and the 3Hydrogens. i have also included the LCAO's (linear combined atomic orbitals) and the computed molecular orbitals. The LCAO where all pre-drawn in ChemDraw using Dr Hunt's 2nd year lecture notes as a guide.
From the diagram above we can see the LCAO's and almost exact to the computed molecular orbitals, this shows how accuracy of the method and basis set used!!
NBO analysis using NH3
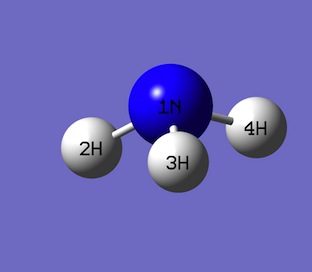
Steps that lead to the NBO analysis; Firstly, a NH3 molecule was drawn in GuassView. Then the molecule was optimised using basis set 6-31G(d,p) and 'nosymm' was added to the additional key words section.
Optimisation of NH3
Optimisation results shown below.
| File name | NH3_OPT_DTF_YFnew |
| File Type | .log |
| Calculation type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -56.55766654 a.u. |
| RMS Gradient Norm | 0.00003962 |
| Imaginary Freq | |
| Dipole Moment | 1.8463 Debye |
| Point Group | C1 |
D1 -1.95257 0.00002 0.00000 0.00024 0.00024 -1.95233
Item Value Threshold Converged?
Maximum Force 0.000079 0.000450 YES
RMS Force 0.000045 0.000300 YES
Maximum Displacement 0.000216 0.001800 YES
RMS Displacement 0.000139 0.001200 YES
Predicted change in Energy=-1.898827D-08
Optimization completed.
The information box above, method and basis calculations where imposed and optimisation was successfully complete.
| Bond type | Bond Length  |
|---|---|
| N-H(2) | 1.018 |
| N-H(3) | 1.018 |
| N-H(4) | 1.018 |
| Bond type | Bond angle ° |
|---|---|
| H(2)-N-H(3) | 105.7 |
| H(3)-N-H(4) | 105.7 |
| H(4)-N-H(2) | 105.7 |
Frequency Analysis of NH3
Low frequencies --- -3.5501 -1.0013 -0.0005 0.0016 0.3517 7.8876 Low frequencies --- 1089.7832 1694.1620 1694.3220
frequencies are due to the motions of the center of mass of the molecule and are within an acceptable range of +/- 15 cm-1. They are an order of magnitude smaller than the "real" frequencies found on the second line.
| File name | NH3_NH3_FREW_NEW |
| File Type | .log |
| Calculation type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -56.55776854 a.u. |
| RMS Gradient Norm | 0.00003962 |
| Imaginary Freq | |
| Dipole Moment | 1.8463 Debye |
| Point Group | C1 |
Molecular Orbital analysis of NH3
For the MO analysis, the optimised molecule was opened and saved under a new name "NH3_NBO_NEW" and now different calculation setup was done, the job type 'Optimization' was changed to 'energy', and under the NBO tab NBO pull dwon was changed from 'none' to 'FULL NBO' and lastly, in the additional keyword section the phase 'pop=full' was added. When submitted, the .chk file was opened with the reactive intermediates box 'ticked'.
log file: File:NH3 NBO NEW.log
chk file:File:NH3 NBO NEW.chk
| File name | NH3_NBO_NEW |
| File Type | .log |
| Calculation type | SP |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -56.55776854 a.u. |
| RMS Gradient Norm | 0.00003962 |
| Imaginary Freq | |
| Dipole Moment | 1.8463 Debye |
| Point Group | C1 |
NBO analysis of NH3
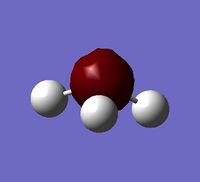
To collect information on the charge distribution, the .log file for calculated molecular orbitals was opened. Under 'Results' in the tap along the top, 'Charge Distribution' was opened. The atomic charge type was changed from 'Mulliken' to 'NBO', and charge range set from -1.000 to +1.000.
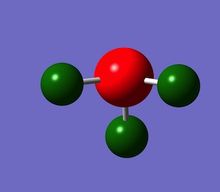
The Red coloured Nitrogen atom, indicates a negative charge, as what would be expected do to its lone pair of electrons. The green colours Hydrogen atoms indicate a positive charge.
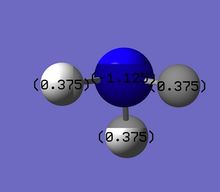
The NBO charges for nitrogen is negative charge,-1.125, and hydrogen a positive charge, 0.325. This distribution is as expected given the electronegative nature of nitrogen, withdrawing electron from the three hydrogens, with an sum/overall charge of 0.
Below summarises the charge distribution in NH3
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
N 1 -1.12518 1.99982 6.11108 0.01429 8.12518
H 2 0.37506 0.00000 0.62248 0.00246 0.62494
H 3 0.37506 0.00000 0.62248 0.00246 0.62494
H 4 0.37506 0.00000 0.62249 0.00246 0.62494
=======================================================================
* Total * 0.00000 1.99982 7.97853 0.02166 10.00000
Hybridisation in NH3
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.99909) BD ( 1) N 1 - H 2
( 68.83%) 0.8297* N 1 s( 24.87%)p 3.02( 75.05%)d 0.00( 0.09%)
-0.0001 -0.4986 -0.0059 0.0000 -0.2910
0.0052 0.8155 0.0277 0.0000 0.0000
0.0281 0.0000 0.0000 0.0032 0.0082
( 31.17%) 0.5583* H 2 s( 99.91%)p 0.00( 0.09%)
-0.9996 0.0000 0.0072 -0.0289 0.0000
2. (1.99909) BD ( 1) N 1 - H 3
( 68.83%) 0.8297* N 1 s( 24.87%)p 3.02( 75.05%)d 0.00( 0.09%)
0.0001 0.4986 0.0059 0.0000 0.2910
-0.0052 0.4078 0.0138 0.7062 0.0239
0.0140 0.0243 0.0076 0.0033 0.0031
( 31.17%) 0.5583* H 3 s( 99.91%)p 0.00( 0.09%)
0.9996 0.0000 -0.0072 -0.0145 -0.0250
3. (1.99909) BD ( 1) N 1 - H 4
( 68.83%) 0.8297* N 1 s( 24.86%)p 3.02( 75.05%)d 0.00( 0.09%)
0.0001 0.4986 0.0059 0.0000 0.2909
-0.0052 0.4078 0.0138 -0.7063 -0.0239
0.0140 -0.0243 -0.0076 0.0033 0.0031
( 31.17%) 0.5583* H 4 s( 99.91%)p 0.00( 0.09%)
0.9996 0.0000 -0.0072 -0.0145 0.0250
4. (1.99982) CR ( 1) N 1 s(100.00%)
1.0000 -0.0002 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
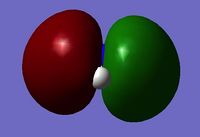
5. (1.99721) LP ( 1) N 1 s( 25.38%)p 2.94( 74.52%)d 0.00( 0.10%)
0.0001 0.5037 -0.0120 0.0000 -0.8618
0.0505 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 -0.0269 0.0155
Table below summarises information in a clearer presentation.
| Nature of Bond | Hybridization |
|---|---|
| N 68.83% H(2) 31.17% | Nitrogen 24.87%s 75.05%p Hydrogen 100%s |
| N 68.83% H(3) 31.17% | Nitrogen 24.87%s 75.05%p Hydrogen 100%s |
| N 68.83% H(3) 31.17% | Nitrogen 24.87%s 75.05%p Hydrogen 100%s |
| Core nitrogen orbital | Nitrogen 100.00%s |
| Lone pair nitrogen | Nitrogen 24.38%s 75.52%p |
A greater contribution from Nitrogen (69%) than hydrogen (31%) in the N-H bond due to its greater electronegtivety. The nitrogen hybridisation is 24.87%s 75.05%p, ratio of s:p contribution is 1:3, which means nitrogen has a hybridisation of sp3.The lone pair has '24.38%s 75.52%p character, i.e sp3 hybrid,
NH3BH3
Optimisation
Item Value Threshold Converged? Maximum Force 0.000128 0.000450 YES RMS Force 0.000057 0.000300 YES Maximum Displacement 0.000644 0.001800 YES RMS Displacement 0.000378 0.001200 YES Predicted change in Energy=-1.666226D-07 Optimization completed.
| File name | NH4BH3_OTP | cell |
| File Type | .log | |
| Calculation type | FOPT | |
| Calculation Method | RB3LYP | |
| Basis Set | 6-31G(d,p) | |
| Charge | 0 | |
| Spin | Singlet | |
| E(RB3LYP) | -83.2247899 | a.u. |
| RMS Gradient Norm | 0.00006031 | a.u. |
| Imaginary Freq | ||
| Dipole Moment | 5.5650 | Debye |
| Point Group | C1 |
| Bond type | Bond Length  |
|---|---|
| B-H | 1.01859 |
| B-N | 1.66808 |
| N-H | 1.21004 |
| Bond type | Bond angle ° |
|---|---|
| H-B-N | 111.026 |
| H-N-B | 104.599 |
| H-B-H | 107.871 |
| H-N-H | 113.874 |
Frequency
Using the optimised 6-31G(d,p) file, we changed the job type to frequency leaving all other calculations the same and submitted molecule to run.
Full mass-weighted force constant matrix: Low frequencies --- -2.2121 -1.1044 -0.0001 0.0004 0.0005 4.3753 Low frequencies --- 266.1280 632.3146 639.0903
| File name | NH4BH3_FREQ |
| File Type | .log |
| Calculation type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -83.22468973 a.u. |
| RMS Gradient Norm | 0.00006037 a.u. |
| Imaginary Freq | |
| Dipole Moment | 5.5650 Debye |
| Point Group | C1 |
Energies analysis
To calculate the computed energy of NH3BH3, we used the follow equation ΔE= E(NH3BH3)-E(NH3)-E(BH3)
E(NH3BH3)= -83.2247899 a.u.
E(NH3)= -56.55766654 a.u.
E(BH3)= -26.61544289 a.u.
Therefore, ΔE= (-83.2247899 a.u.) -(-56.55766654 a.u.)-(-26.61544289 a.u.) = -0.05168 a.u. = -135.687 kJ/mol
The association energy for combining a molecule of NH3 with one of BH3 it the ΔE we calculated in Kj/mol above, which is -135.4720296 kJ/mol.
conversely this is also the bond dissociation energy: EBD = 135.4720296 kJ/mol
Frequency:
Low frequencies --- -0.0011 -0.0009 0.0006 18.2727 22.8004 41.2546
Low frequencies --- 266.2767 632.3269 639.2666
To calculate the computed energy of NH3BH3, we used the follow equation ΔE= E(NH3BH3)-E(NH3)-E(BH3)
E(NH3BH3)= -83.22468999 a.u.
E(NH3)= -56.55776854 a.u.
E(BH3)= -26.61532289 a.u.
Therefore, ΔE= (-83.22468999 a.u.) -(-56.55776854 a.u.)-(-26.61532289 a.u.) = -0.05159856 a.u. = -135.4720296 kJ/mol
the association energy for combining a molecule of NH3 with one of BH3 it the ΔE we calculated in Kj/mol above, which is -135.4720296 kJ/mol.
conversely this is also the bond dissociation energy: EBD = 135.4720296 kJ/mol
Reference’s:
1. Kawaguchi, Kentarou (1992). "Fourier transform infrared spectroscopy of the BH3 ν3 band". The Journal of Chemical Physics 96 (5):
2. Ullmann's Fine Chemicals edited by Wiley-VCH page 346 3.↑ Balázs Réffy, Mária Kolonits, Magdolna Hargittai, Gallium tribromide: molecular geometry of monomer and dimer from gas-phase electron diffraction, Journal of Molecular Structure, Volume 445, Issues 1–3, 6 April 1998, Pages 139-148, ISSN 0022-2860,