Rep:Mod:yellowsaints
Joe Downey Experiment 1C
The Hydrogenation of Cyclopentadiene Dimer
Exo vs Endo Dimerisation

Cyclopentadiene when left at room temperature will dimerise to form the endo dimer (2) as shown here [1] To investigate why this reaction shows a preference for the formation of the endo dimer, the geometries of both (1) and (2) were optimised with the MMFF94s forcefield and the energies calculated in Avogadro.
| Energy | (1) Exo Dimer (kcal/mol) | (2) Endo Dimer (kcal/mol) |
|---|---|---|
| Bond Stretching | 3.54307 | 3.46506 |
| Angle Bending | 30.77272 | 33.21463 |
| Stretch Bending | -2.0414 | -2.08154 |
| Torsional | -2.7311 | -2.9491 |
| Out-of-Plane Bending | 0.01485 | 0.02107 |
| Van der Waals | 12.80159 | 12.34089 |
| Electrostatic Interactions | 13.01372 | 14.17979 |
| Total Energy | 55.34344 | 58.1908 |
These values simply illustrate how far each of these energies deviate from ideality. Unlike a normal thermodynamic value (such as free energy or enthalpy) this value cannot be compared between entirely different molecules. However it is of value in giving an idea of the relative thermodynamic stabilities of two isomers. Hence these calculations show a slight thermodynamic stability in favour of the exo dimer (1).
This suggests that the thermodynamic product of cyclopentadiene dimerisation is the exo dimer. This seems contrary to the documented preference ion the literature of the endo form. If the thermodynamic form is not produced at room temperature, then this would suggest that this dimerisation process is in fact, kinetically controlled. The work by Wilson and Wells[1] supports this theory, by demonstrating that at higher temperatures dimerisation gives a mixture of the thermodynamic exo-form, and the kinetic endo-form.
If the endo form is the kinetic product, the formation of the endo dimer must therefore go via a lower energy transition state than the exo form. This has been confirmed in the literature and has been attributed to orbital effects [2].
Dihydrogenation Selectivity

The endo dimer (2) will go on to hydrogenate at either of its two double bonds to form either (3) or (4). To calculate which hydrogenation product was more thermodynamically likely, the molecular geometries were again optimised with the MMFF94s forcefield and the energies calculated in Avogadro.
| Energy | (3) Dihydro Derivative (kcal/mol) | (4) Dihydro Derivative (kcal/mol) |
|---|---|---|
| Bond Stretching | 3.3065 | 2.82313 |
| Angle Bending | 30.85157 | 24.68529 |
| Stretch Bending | -1.92617 | -1.65719 |
| Torsional | 0.08126 | -0.37848 |
| Out-of-Plane Bending | 0.0152 | 0.00028 |
| Van der Waals | 13.27349 | 10.63744 |
| Electrostatic Interactions | 5.121 | 5.14702 |
| Total Energy | 50.72285 | 41.25749 |
As can be seen from the results in the table above, (3) is favoured thermodynamically over (4). This is supported by the literature data[3] suggesting that formation of (3) is heavily favoured over that of (4). If the formation of the thermodynamic product dominates the reaction, it can be assumed to be under thermodynamic control.
Atropisomerism of a Taxol Intermediate
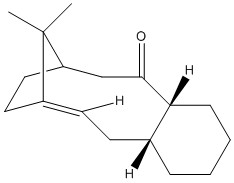
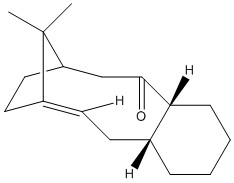
The molecules (9) and (10) are intermediates in the synthesis of the drug Taxol. These molecules are a good example of Atropisomerism, where isomerism arises through hindered rotation about a single bond.
To determine which of these atropisomers is more thermodynamically stable, the molecular geometries were optimised with the MMFF94s forcefield and the energies calculated in Avogadro.
| Energy | (9) Atropisomer (Taxol Intermediate) (kcal/mol) | (10) Atropisomer (Taxol Intermediate) (kcal/mol) |
|---|---|---|
| Bond Stretching | 7.63086 | 7.57978 |
| Angle Bending | 28.26511 | 18.83144 |
| Stretch Bending | -0.08167 | -0.14205 |
| Torsional | 0.33596 | 0.31308 |
| Out-of-Plane Bending | 0.96761 | 0.84208 |
| Van der Waals | 33.13195 | 33.18703 |
| Electrostatic Interactions | 0.30717 | -0.04700 |
| Total Energy | 70.557 | 60.56436 |
As can be seen from the values above, (10) is of a lower energy than (9). This suggests that since (10) is more thermodynamically stable than (9), when left for extended periods of time, atropisomer (9) undergoes bond rotation to form the more thermodynamically stable atropisomer (10).
These two conformations are the two most stable conformations of these atropisomers. The feature which will exert the biggest stabilising effect on the molecule is the conformation of the terminal cyclohexyl group. In both of these isomers, the cyclohexyl groups are sitting in the chair conformation. This is the lowest energy conformation of the cyclohexyl rings and so exerts enough of a stabilising effect on the torsional energy contribution that these are the lowest energy conformations available.
The energetic barrier for interconversion between these two isomers must therefore, in part, arise from ring flipping of this cyclohexyl group. Ring flipping is required since the ring adopts the conformation whereby the spatially closest methylene carbons distance themselves from the carbonyl oxygen by moving to an antiperiplanar position, and the major difference between (9) and (10) is the carbonyl orientation. Hence ring flipping is required for interconversion between (9) and (10).
This dihydrogenation has been found to be unusually slow since these molecules are unusually stable towards hydrogenation of the alkene. This effect has lead to molecules of this sort being considered "hyperstable olefins"[4].
Typically, an alkene at a bridgehead carbon is considered very unfavourable due to Bredt's rule[4] but it is suggested that when a trans-cycloalkene reaches a certain size, that a so called "Anti-Bredt" molecule (with an alkene at the bridgehead carbon) will actually be relatively stabilised. The unusual unreactivity of (9) and (10) suggests that these are both examples of "Anti-Bredt" molecules.
This hyperstabilization arises from the fact that once a ring reaches a certain size, the bridgehead alkene is actually less sterically strained than the respective hydrogenation product alkane. Hence these atropisomers are both stabilised towards hydrogenation by the presence of a hyperstable olefin[4].
Spectroscopic Simulation Using Quantum Mechanics (Part 1)
Relative Isomeric Stabilities
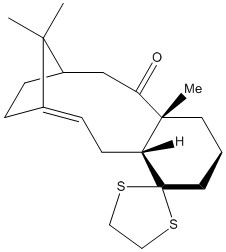
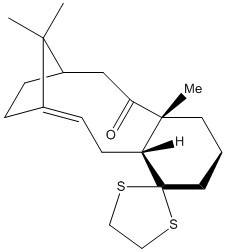
Molecules (17) and (18) are also atropisomers involved in the synthesis of Taxol. To determine which of these atropisomers is more thermodynamically stable, the molecular geometries were optimised with the MMFF94s forcefield and the energies calculated in Avogadro. These energies are tabulated below.
| Energy | (17) Atropisomer (Taxol Intermediate) (kcal/mol) | (18) Atropisomer (Taxol Intermediate) (kcal/mol) |
|---|---|---|
| Bond Stretching | 25.53968 | 24.5769 |
| Angle Bending | 62.733 | 51.6524 |
| Stretch Bending | 0.92086 | -0.43356 |
| Torsional | 29.84379 | 35.66169 |
| Out-of-Plane Bending | 4.24649 | 4.23427 |
| Van der Waals | 66.10198 | 67.19367 |
| Electrostatic Interactions | -5.60003 | -4.66152 |
| Total Energy | 183.78577 | 178.22385 |
As can be seen above, the atropisomer (18) is marginally more stable than (17). This could be due in part to steric clashes, present in (17), between the carbonyl oxygen and the methyl groups adjacent and on the bridgehead, which are not present in (18). Further NCI calculations would be able to confirm this theory, but were not possible given current time constraints.
| ΔG (Sum of Electronic and Thermal Free Energies) (kJ/mol) | |
|---|---|
| (17) | -4335627.413854 |
| (18) | -4335644.521613 |
| Difference in ΔG | 17.11 |
These free energies were extracted from an NMR calculation. The NMR spectra of both (17) and (18) were calculated using the B3LYP DFT Method and the 6-31G(d,p) basis set.
This free energy difference is in alignment with the energies arising from the molecular geometry optimization performed earlier and supports the conclusion that (18) is thermodynamically more stable than (17).
NMR Calculation


The NMR spectra of both (17) DOI:10042/27381 and (18) DOI:10042/27382 were calculated using the B3LYP DFT Method and the 6-31G(d,p) basis set. These NMR Spectra are in good agreement with the literature data[5] in that they show the expected pattern and characteristic chemical shifts.
The major issue here is that it appears that the NMR spectra are calculated for a static picture of the molecule. Because of this, none of the "dynamic" features of a molecule are captured. For example, methyl groups (unless severely hindered) will rotate about the C-C bond and result in averaging and aggregation of these three individual chemical shifts into one. So chemical shifts reported as integrating to 3H in the literature will in this case appear as three individual and comparatively distant chemical shifts in the calculated spectra. This is a major drawback in comparing calculated and real NMR spectra of complicated molecules.
Asymmetric Epoxidation of Alkenes (Part 2)
Shi and Jacobsen Catalysts

The Shi And Jacobsen Catalysts are two catalytic systems used for the asymmetric epoxidation of Alkenes. In the follwing section, these catalysts as well as several of their reactions are investigated using NMR, Optical rotation and NCI/QTAIM analysis of the electronics of the transition states.
CCDC Searches and Analysis
Shi Precatalyst

The shi precatalyst (21) has three anomeric centres. A crystal structure of this molecule was found[6] and the bond lengths were measured in Mercury. The bond lengths as seen on the right are clearly not all of the same length. 2 Bonds in particular were found to be longer than the 4 others. These length differences could possibly be attributed to the substituents on the Oxygens in these ketal groups due to the documented "anomeric effect"[7].
Jacobsen Precatalyst
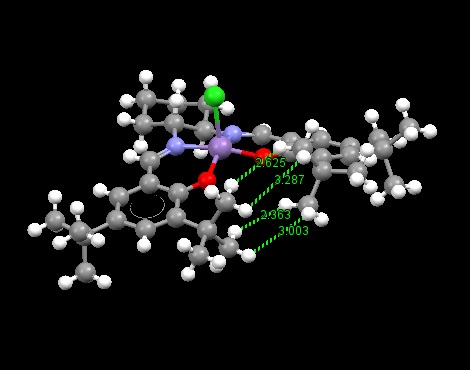
A crystal structure of this molecule was found[8] and the H-H separations between the two adjacent tBu groups was measured in Mercury.
As can be seen, one inter-hydrogen distance was measured to be 2.363 Å. Since the Van der Waals radius of one hydrogen atom is approximately 1.20 Å. This means that the metal centre is inaccessible to approach from the side, encouraging attack from one particular face - the active site.
Epoxidation of Styrene

Epoxidation of Styrene with either the Shi or Jacobsen Catalyst will result in either the (R)- or (S)-epoxide being formed as shown in the scheme to the right. To determine which enantiomer is produced, there are several options available to aid in assignment of absolute configuration. NMR will help in verifying that Styrene Oxide is produced, but is not so useful in determining absolute configuration since either enantiomer will give the same chemical shifts in 1H NMR. For this, it is much more useful to calculate the optical rotation of each enantiomer and compare it to experimental data.
NMR Calculations
The NMR spectra of both (R) DOI:10042/27391 and (S) DOI:10042/27388 were calculated using the B3LYP DFT Method and the 6-31G(d,p) basis set. The results for (R) are tabulated below and compared with literature values[9].
| Calculated 1H Chemical Shift (ppm) | Literature 1H Chemical Shift (ppm) | Calculation vs Literature Discrepancy (ppm) |
|---|---|---|
| 2.54 | 2.75 | -0.21 |
| 3.11 | 3.08 | 0.03 |
| 3.66 | 3.8 | -0.14 |
| 7.30-7.51 | 7.24-7.33 | n/a |
The experimental 1H NMR spectrum of Styrene Oxide is relatively simple and characteristic, with three singlets at around 2.5-4.0 ppm and then a multiplet of aromatic protons from the phenyl group at around 7.0-8.0 ppm. The calculated NMR spectrum is very similar to this and suggests that the calculation was run correctly.

| Calculated 13C Chemical Shift (ppm) | Literature 13C Chemical Shift (ppm) | Calculation vs Literature Discrepancy (ppm) |
|---|---|---|
| 53.05 | 51 | 2.05 |
| 53.46 | 51.1 | 2.36 |
| 118.268 | 125.3 | -7.032 |
| 123.415 | 128 | -4.585 |
| 124.133 | 128.2 | -4.067 |
| 135.135 | 137.5 | -2.365 |
This NMR calculation again appears to be relatively consistent with the literature, reinforcing the conclusion that the calculation was run correctly.
Optical Rotation
Enatiomers will rotate plane polarised light, and opposite enantiomers will rotate this light by the same amount but in opposite directions. Because of this, optical rotation can be a powerful tool in assigning the absolute configurations of enantiomers.
The optical rotation values at 589nm and 365nm for both (R) DOI:10042/27386 and (S) DOI:10042/27389 Styrene Oxide were calculated using the CAM-B3LYP/6-311++g(2df,p) method on already QM-optimised structures. These results are tabulated and compared with literature values[10] below.
| Calculated Optical Rotation (°) | Literature Optical Rotation (°) | |
|---|---|---|
| (R) Styrene Oxide 589nm | -30.1 | -33.3 |
| (S) Styrene Oxide 589nm | 30.1 | 33 |
| (R) Styrene Oxide 365nm | -93.98 | n/a |
| (S) Styrene Oxide 365nm | 93.98 | n/a |
These values are in line with the literature for 589 nm (no data was available for 365 nm). In addition to this, the fact that opposite enantiomers have opposite signs suggests that the calculations were run correctly.
NCI and QTAIM
NCI
Non covalent interaction analysis on DFT calculations (performed by H Rzepa) shows areas with positive interatomic and intermolecular electronic interactions. The green areas indicate areas of positive interaction, the red areas indicate negative. This analysis helps in this case by indicating what interactions have lead to the transition state adopting the shape it has.
Non covalent analysis of one pre-calculated transition state of the (R)-epoxidation of Styrene with the Jacobsen catalyst was performed using Gaussview and is available as a 3D JMol below.
NCI |
It can be seen here that in this transition state, the epoxide is halfway through forming. One C-O bond is formed, and the other bond is not present nor are there any attractive NCIs between the Oxygen and the Carbon it will go on to form a bond with.
In this NCI analysis it is clear that the major beneficial NCI is between the π-systems on the Styrene phenyl group and one of the phenyl groups on the Jacobsen catalyst. There are large positive NCIs in the region between these two rings and so they tend to stack above one another, bringing the alkene into a good proximity to the oxygen thus allowing facile epoxidation. This is the basis behind this molecule's catalytic ability.
There are however some small regions of negative NCIs present. Particularly around the Mn centre, where there is some visible ligand-ligand repulsion. This suggests that with different ligands present and without other more-stabilising NCIs the ligands about the Mn centre would rearrange to a less strained geometry.
QTAIM

QTAIM is a similar theory to NCI in that it shows areas where attractive interactions are strong enough that a bond is at least partially formed between two atoms. It has been suggested that it is not as useful as NCI since it only shows bond-critical-points and doesn't show other, less strong, electronic interactions[11].
QTAIM analysis was carried out on the same transition state as the NCI Analysis. Here it is very clear to see the first epoxide bond being formed as one can see the bond critical point between the Oxygen and the alkene Carbon (orange arrow). This makes it clear where the bond being formed is, but doesn't make the NCI interactions between the π-systems as clear as NCI analysis does, since these interactions do not go on to form a bond. They are however, useful to observe, since this makes the catalytic action of this catalyst especially clear.
Epoxidation of 1,2-Dihydronaphthalene

Epoxidation of 1,2-Dihydronapthalene with either the Shi or Jacobsen Catalyst will result in either the (3R,4S)- or (3S,4R)-1,2-dihydronaphthalene epoxide as shown in the scheme to the right. To determine which enantiomer is produced, there are several options available to aid in assignment of absolute configuration. NMR will help in verifying that the epoxide is produced, but is not so useful in determining absolute configuration since either enantiomer will give the same chemical shifts in 1H NMR. For this, it is much more useful to calculate the optical rotation of each enantiomer and compare it to experimental data.
NMR Calculations
The NMR spectra of both (3S,4R) DOI:10042/27387 and (3R,4S) DOI:10042/27390 were calculated using the B3LYP DFT Method and the 6-31G(d,p) basis set. The results for (3S,4R) are tabulated below and compared with literature values[12].

| Calculated 1H Chemical Shift (ppm) | Literature 1H Chemical Shift (ppm) | Calculated vs Literature Discrepancy (ppm) |
|---|---|---|
| 1.88 | 1.67 | 0.21 |
| 2.21 | 2.33 | -0.12 |
| 2.27 | 2.45 | -0.18 |
| 2.95 | 2.67 | 0.28 |
| 3.49 | 3.65 | -0.16 |
| 3.56 | 3.78 | -0.22 |
| 7.26 | 7.01 | 0.25 |
| 7.39 | 7.17 | 0.22 |
| 7.62 | 7.33 | 0.29 |
The experimental 1H NMR spectrum of Dihydronaphthalene Oxide is also relatively simple, with two characteristic regions - the protons in the aromatic system at around 7.0-8.0 ppm and the protons on the non-aromatic cyclohexyl group at around 1.5-4.0 ppm. The calculated NMR spectrum is very similar to this and suggests that the calculation was run correctly.

| Calculated 13C Chemical Shift (ppm) | Literature 13C Chemical Shift (ppm) | Calculated vs Literature Discrepancy |
|---|---|---|
| 29.06 | 22.19 | 6.87 |
| 30.18 | 24.78 | 5.4 |
| 52.19 | 55.16 | -2.97 |
| 52.82 | 55.52 | -2.7 |
| 121.74 | 126.51 | -4.77 |
| 123.53 | 128.8 | -5.27 |
| 123.79 | 128.83 | -5.04 |
| 126.67 | 129.94 | -3.27 |
| 130.71 | 132.91 | -2.2 |
| 135.39 | 137.07 | -1.68 |
This NMR calculation again appears to be relatively consistent with the literature showing no major deviations thus reinforcing the conclusion that the calculation was run correctly.
Optical Rotations
The optical rotation values at 589nm and 365nm for both (3S,4R)- and (3R,4S)-1,2-dihydronaphthalene oxide DOI:10042/27385 were calculated using the CAM-B3LYP/6-311++g(2df,p) method on already QM-optimised structures. These results are tabulated and compared with literature values [13]
| Calculated Optical Rotation (°) | Literature Optical Rotation (°) | |
|---|---|---|
| (3S,4R)-1,2-Dihydronaphthalene Oxide 589nm | -35.86 | 129 |
| (3R,4S)-1,2-Dihydronaphthalene Oxide 589nm | 35.87 | -39 |
| (3S,4R)-1,2-Dihydronaphthalene Oxide 365nm | -209.45 | n/a |
| (3R,4S)-1,2-Dihydronaphthalene Oxide 365nm | 209.4 | n/a |
Unlike with Styrene Oxide, these optical rotation values are not in as good agreement, as well as there being several wildly varying literature values for the optical rotation at 589 nm (again, no values could be found for 365 nm).
One possible reason for such a large discrepancy between literature and calculation is that optical rotation calculations are very susceptible to the exact structural conformation of the molecule. The QM-optimised structure may not in fact be the preferred conformation at all concentrations and in all different solvents. If, for the values cited in the literature, the epoxide had adopted a slightly different conformer, it could have great effect on the final optical rotation value.
It is important to note that the calculated values here differ only in sign, as expected from the theory.
References
- ↑ 1.0 1.1 Philip J. Wilson and Joseph H. Wells, The Chemistry and Utilization of Cyclopentadiene, Chemical Reviews 1944 34 (1), 1-50
- ↑ Sauer J and Sustmann R, "Mechanistic Aspects of Diels-Alder Reactions: A Critical Survey", Angew. Chem. Int. Ed. Engl., 1980, 19, 779-807
- ↑ Skala and Hanika, "Kinetics of Dicyclopentadiene Hydrogenation using Pd/C Catalyst", Petroleum and Coal, 2003, 45, 3-4
- ↑ 4.0 4.1 4.2 Maier W and Schleyer P, "Evaluation and prediction of the stability of bridgehead olefins", J. Am. Chem. Soc., 1981, 103 (8), 1891–1900
- ↑ Paquette L et. al, "[3.3] Sigmatropy within 1-vinyl-2-alkenyl-7,7-dimethyl-exo-norbornan-2-ols. The first atropselective oxyanionic Cope rearrangement", J. Am. Chem. Soc., 1990, 112 (1), 277–283
- ↑ Wang Z, Miller S and Shi Y, "Asymmetric Epoxidation by Chiral Ketones Derived from Carbocyclic Analogues of Fructose", J. Org. Chem., 2001, 66 (2), 521–530
- ↑ Briggs A and Glenn R, "Bond length and reactivity. Stereoelectronic effects on bonding in acetals and glucosides", J. Am. Chem. Soc., 1984, 106 (21), 6200–6206
- ↑ Yoon J, "(1R,2R)-(-)-[Bis(3,5-di-tert-butylsalicylidene)-1,2-cyclohexanediamine]chloromanganese(III), an (R,R)-Jacobsen catalyst", Acta Cryst. (1999). C55. 1766-1769
- ↑ Wiles C, "The development and evaluation of a continuous flow process for the lipase-mediated oxidation of alkenes", Beilstein J. Org. Chem. 2009, 5, 27
- ↑ Jensen F, "Stereochemistry and mechanism of the photochemical and thermal insertion of oxygen into the carbon-cobalt bond of alkyl(pyridine)cobaloximes", J. Am. Chem. Soc., 1975, 97 (20), 5825–5831
- ↑ Lane J, "Are Bond Critical Points Really Critical for Hydrogen Bonding?", J. Chem. Theory Comput., 2013, 9 (8), 3263–3266
- ↑ Jacobsen E and Larrow J, "Kinetic Resolution of 1,2-Dihydronaphthalene Oxide and Related Epoxides via Asymmetric C-H Hydroxylation", J. Am. Chem. Soc., 1994, 116 (26), pp 12129–12130
- ↑ Archelas A, "Microbiological transformation 32: Use of epoxide hydrolase mediated biohydrolysis as a way to enantiopure epoxides and vicinal diols: Application to substituted styrene oxide derivatives", Tetrahedron, 1996, 52 (13), 4593-4606
