Rep:Mod:yb3818 complabs
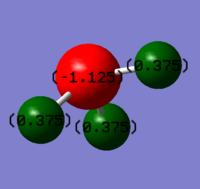
NH3 molecule
The diagram shows NH3 (or ammonia) created using GaussView
Calculation method: RB3LYP Basis set: 6-31G(d,p)
The final energy of the optimised molecule: -56.55776873 a.u.
RSM Gradient: 0.00000485 a.u.
Point group of the molecule: C3v
N-H bond length: 1.02Å
H-N-H bond angle: 106°
| Item | Value | Threshold | Converged? |
|---|---|---|---|
| Maximum Force | 0.000005 | 0.00450 | YES |
| RMS Force | 0.000003 | 0.000300 | YES |
| Maximum Displacement | 0.000012 | 0.001800 | YES |
| RMS Displacement | 0.000008 | 0.001200 | YES |
Optimised Ammonia molecule |
The optimisation file is liked to here
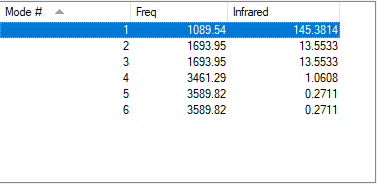
Vibrational data for ammonia:
| wavenumber/ cm-1 | 1090 | 1694 | 1694 | 3461 | 3590 | 3590 |
|---|---|---|---|---|---|---|
| symmetry | A1 | E | E | A1 | E | E |
| IR intensity | 145 | 14 | 14 | 1 | 0 | 0 |
| image |  |
 |
 |
 |
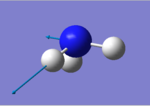 |
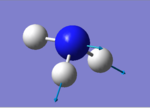
|
Ammonia molecule is expected to have 6 vibrational nodes (3N-6 rule, where N is the number of atoms in the molecule). There are two vibrational nodes that appear at 1694 cm-1 and two vibrational nodes at 3590 cm-1. Two vibrational nodes that occur at the same wavenumber are considered to be degenerate. 5 vibrations represent "bond stretches"(1694,3461 and 3590 cm-1) and mode at 1090 cm-1 represents "bending" mode. The latter mode is commonly known as "umbrella" mode. Out of six modes, only four vibrations can be detected by spectrometer. However, since there are two pairs of degenerate modes, only two peaks appear in an experimental spectrum of ammonia. For 3590 cm-1 the intensity is zero, therefore it is not seen.
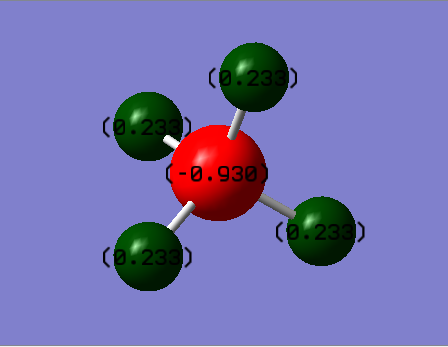
Charges of atoms in ammonia molecule:
We would expect nitrogen to be negatively charged and all of the three hydrogen atoms positively charged. Nitrogen is more electronegative and therefore pulls electron density away from hydrogen atoms.
N2 molecule
N2 molecule was created in GaussView using RB3LYP method and 6-31G(d,p) as a basis set. The final energy of the optimised molecule was found to be -109.52412868 a.u. Molecule has D∞H point group. The length of a triple bond between nitrogen atoms is found to be 1.11 Å to 3 sig.fig. Since nitrogen molecule is diatomic, the bond angle appears to be 0°.
| Item | Value | Threshold | Converged? |
|---|---|---|---|
| Maximum Force | 0.000001 | 0.004500 | YES |
| RMS Force | 0.000001 | 0.000300 | YES |
| Maximum Displacement | 0.000000 | 0.001800 | YES |
| RMS Displacement | 0.000000 | 0.001200 | YES |
Optimised Nitrogen gas molecule |
The optimisation file is liked to here
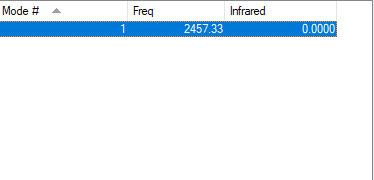
The following data about vibrations of N2 molecule was obtained:
From the table above nitrogen gas molecule has only one vibration at 2457 cm-1 as expected - for any linear molecule there are 3N-5 vibrational modes. This vibration represents N-N bond stretching. The bond is symmetrical, no change in dipole moment is observed and, therefore, the molecule is IR inactive (IR intensity is found to be 0). Table below summarises all of the information:
| wavenumber/ cm-1 | 2457 |
|---|---|
| symmetry | SGG |
| IR intensity | 0 |
| image | 
|
N2 molecule is homo-nuclear diatomic molecule and we would expect to have no charges on nitrogen atoms. GaussView has shown no charges on any of the nitrogen atoms. The picture below shows charge distribution. Both atoms appear black doe to the even charge distribution.
H2 molecule
H2 molecule was created in GaussView using RB3LYP method and 6-31G(d,p) as a basis set. The final energy of the optimised molecule was found to be -1.17853936 a.u. Molecule has D∞H point group. The length of a bond between hydrogen atoms is found to be 0.743 Å to 3 sig.fig. Since hydrogen molecule is diatomic, the bond angle appears to be 0°.
| Item | Value | Threshold | Converged? |
|---|---|---|---|
| Maximum Force | 0.000001 | 0.000450 | YES |
| RMS Force | 0.000001 | 0.000300 | YES |
| Maximum Displacement | 0.000000 | 0.001800 | YES |
| RMS Displacement | 0.000000 | 0.001200 | YES |
Optimised Hydrogen gas molecule |
The optimisation file is liked to here
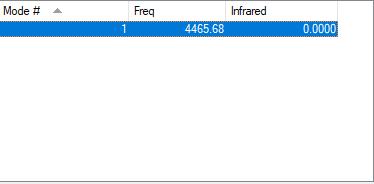
The following data about vibrations of H2 molecule was obtained:
From the table above hydrogen gas molecule has only one vibration at 4466 cm-1 as expected - for any linear molecule there are 3N-5 vibrational modes. This vibration represents H-H bond stretching. The bond is symmetrical, no change in dipole moment is observed and, therefore, the molecule is IR inactive (IR intensity is found to be 0). Table below summarises all of the information:
| wavenumber/ cm-1 | 4466 |
|---|---|
| symmetry | SGG |
| IR intensity | 0 |
| image | 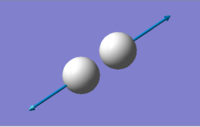
|
H2 molecule is homo-nuclear diatomic molecule and we would expect to have no charges on hydrogen atoms. GaussView has shown no charges on any of the hydrogen atoms. The picture below shows charge distribution. Both atoms appear black doe to the even charge distribution.
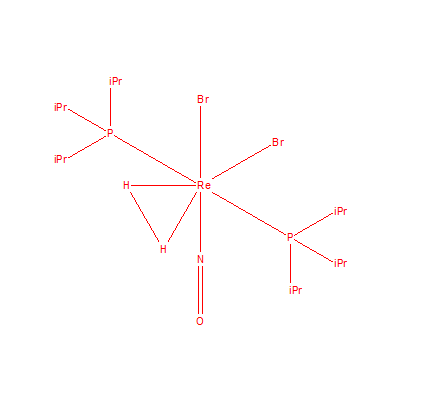
Mono-metalic Transition Metal complex with H2
bis(Tri-isopropylphosphine)-(dihydrogen-H,H')-nitrosyl-dibromo-rhenium has a unique identifier HIVYAM.
The CCDS file of this molecule is liked to here
In the crystal structure H-H bond appears to be 1.11 Å. The bond length obtained after optimisation is 0.743 Å. The bond length is longer in the complex, because the central atom of Rhenium pulls electron density of the bond towards itself, making the H-H bond weaker. We are using Quantum mechanics to compute the bond length which is just approximation and differ to what happens in reality.
Harber-Bosch
Reaction: N2+3H2 -> 2NH3
E(NH3)= -56.5577687 a.u.
2*E(NH3)= -113.1155374 a.u.
E(N2)= -109.5241287 a.u.
E(H2)= -1.1785394 a.u.
3*E(H2)= -3.5356182 a.u.
ΔE=2*E(NH3)-[E(N2)+3*3*E(H2)]=-0.0557905 a.u.
ΔE in kJ/mol: ΔE=-0.0557905*2625.5=-146.4779578=-146.5 kJ/mol ( to 1 d.p.)
Therefore, the energy of converting hydrogen and nitrogen gas into ammonia gas is -146.5 kJ/mol. The reaction is exothermic meaning that the product (ammonia) is more thermodynamically more stable than reactants (nitrogen and hydrogen gas).
CH4 molecule
Optimisation:
CH4 molecule was created in GaussView using RB3LYP method and 6-31G(d,p) as a basis set. The final energy of the optimised molecule was found to be -40.52401404 a.u. Molecule has TD point group. The length of C-H is found to be 1.09 Å and the bond angle is 109°.
| Item | Value | Threshold | Converged? |
|---|---|---|---|
| Maximum Force | 0.000063 | 0.00450 | YES |
| RMS Force | 0.000034 | 0.000300 | YES |
| Maximum Displacement | 0.000179 | 0.001800 | YES |
| RMS Displacement | 0.000095 | 0.001200 | YES |
Optimised methane molecule |
The optimisation file is liked to here
Vibrations
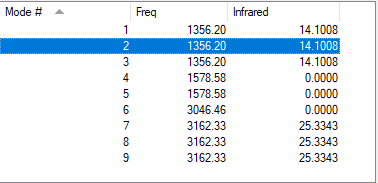
The following data about vibrations of CH4 molecule was obtained:
| wavenumber / cm-1 | symmetry | IR intensity | image |
|---|---|---|---|
| 1356 | T2 | 14 | 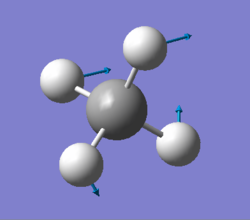
|
| 1356 | T2 | 14 | 
|
| 1356 | T2 | 14 | 
|
| 1578 | E | 0 | 
|
| 1578 | E | 0 | 
|
| 3046 | A1 | 0 | 
|
| 3162 | T2 | 25 | 
|
| 3162 | T2 | 25 | 
|
| 3162 | T2 | 25 | 
|
For any non-linear molecule there are 3N-6 vibrational modes.Therefore, we would predict to see 9 vibrations and this is what is shown in the table above. Modes 4,5 and 6 have zero intensity, therefore they are not seen in IR spectrum. 1,2 and 3 are degenerate as well as 7,8 and 9, therefore only two absorption are seen in IR spectrum of CH4.
Charge:
Carbon is more electronegative than hydrogen, therefore we would expect a negative charge on carbon since it pulls electron density towards itself.
MO's diagrams for methane molecule
The first 9 molecular orbitals were looked at, where three bonding and three antibonding orbitals were found to be degenerate. Here is some information about 5 different orbitals.
1s orbital
This molecular orbital has -10.16707 a.u. From the picture this is 1s carbon atomic orbital, as there is no hydrogen contribution is seen. This AO does not participate in the bonding as it is deep in energy and it is occupied by two electrons.
1σ orbital
This molecular orbital has energy of -0.69041 a.u. 1s orbital of hydrogen atom and 2s carbon orbital are mostly contribute to this MO. This orbital is occupied by two electrons. It is low enough in energy to be a bonding orbital and it contributes to the bond order.
2σ,3σ,4σ
The picture displays 3σ orbital. 2σ,3σ and 4σ are all degenerate but they have different orientation in space. The energy of the three molecular orbitals are found to be -0.38831 a.u. The contribution to each orbital comes mostly from 3s hydrogen orbital and one 2p carbon orbital in x,y and z orientation. All three orbitals contribute to the bond order and each one of them is occupied by 2 electrons. 4σ orbital is a HOMO orbital of the molecule.
5σ*
This picture shows 5σ orbital with the energy of +0.11824. The energy is positive and therefore, this molecular orbital is an antibonding orbital. Contribution to its energy comes mostly from 2s carbon atomic orbital and 1s hydrogen atomic orbital. This orbital is unoccupied and it does not contribute to the bond order. This orbital is a LUMO orbital of the mo
6σ*,7σ*,8σ*
This picture shows 8σ* orbital. 6σ*,7σ* and 8σ* are all degenerate but they have different orientation in space. The energy of these orbitals is found to be +0.17677 a.u. The energy is high and these orbital is an antibonding orbital.This orbital is unoccupied by electrons and does not contribute to the bond order.
Independent work
HCN molecule information:
Optimisation information
HCN molecule was created in GaussView using RB3LYP method and 6-31G(d,p) as a basis set. The final energy of the optimised molecule was found to be -93.42458132 a.u. Molecule has C∞v point group. The length of C-H is found to be 1.07 Å and triple bond between carbon and nitrogen is 1.16 Å and the bond angle is 180°.
| Item | Value | Threshold | Converged? |
|---|---|---|---|
| Maximum Force | 0.000370 | 0.00450 | YES |
| RMS Force | 0.000255 | 0.000300 | YES |
| Maximum Displacement | 0.000731 | 0.001800 | YES |
| RMS Displacement | 0.000459 | 0.001200 | YES |
Optimised HCN molecule |
The optimisation file is liked to here
Vibrations
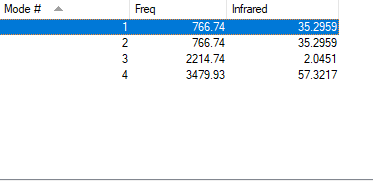
The following data about vibrations of N2 molecule was obtained:
| wavenumber / cm-1 | symmetry | intensity | image |
|---|---|---|---|
| 767 | PI | 35 | 
|
| 767 | PI | 35 | 
|
| 2214 | SG | 2 | 
|
| 3480 | SG | 57 | 
|
For any linear molecule the total number of vibrational modes is 3N-5 (whewre N-number of molecules) HCN molecule should, therefore, have 4 vibrational modes and it is seen from the table above. All four vibrations appear in IR-spectrum, however the first two absorption will overlap since these two vibrations are degenerate; the thirs vibration has a low intensity and might be hard to spot on IR-spectrum.
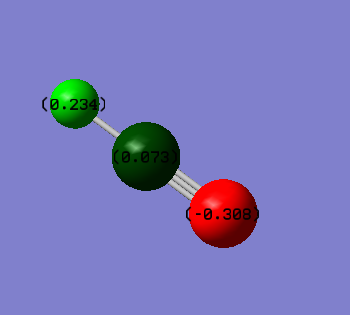
Charge:
Nitrogen is more electronegative than carbon than hydrogen, which means nitrogen will pull electron density towards itself. We would expect Nitrogen atom to be negatively charged, whereas hydrogen should be positively charged. Carbon charge is expected to be in between these two values. By computing the charges, we can see that carbon atom is just slightly positively charged and hydrogen and nitrogen are, indeed, positively and negatively charged particles respectfully.
Marking
Note: All grades and comments are provisional and subject to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have received your grade from blackboard.
Wiki structure and presentation 1/1
Is your wiki page clear and easy to follow, with consistent formatting?
YES
Do you effectively use tables, figures and subheadings to communicate your work?
YES
NH3 1/1
Have you completed the calculation and given a link to the file?
YES
Have you included summary and item tables in your wiki?
YES
Have you included a 3d jmol file or an image of the finished structure?
YES
Have you included the bond lengths and angles asked for?
YES
Have you included the “display vibrations” table?
YES
Have you added a table to your wiki listing the wavenumber and intensity of each vibration?
YES
Did you do the optional extra of adding images of the vibrations?
YES
Have you included answers to the questions about vibrations and charges in the lab script?
YES
N2 and H2 0/0.5
Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges)
YES, However you have given a bond angle of 0 for N2 and H2, there are no bond angles in diatomic molecules. Bond angles involve exactly 3 atoms.
Crystal structure comparison 0.5/0.5
Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule?
YES
Have you compared your optimised bond distance to the crystal structure bond distance?
YES
Haber-Bosch reaction energy calculation 1/1
Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)]
YES
Have you reported your answers to the correct number of decimal places?
YES
Do your energies have the correct +/- sign?
YES
Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product?
YES
Your choice of small molecule 4/5
Have you completed the calculation and included all relevant information?
YES
Have you added information about MOs and charges on atoms?
YES, good explanations overall which are clearly communicated well done! To improve you could have mentioned that the LUMO is antibonding counterpart to the bonding MO 2: the same AOs contribute but with opposite phases rather than the same phase. The same for the sigma * and sigma MOs.
Independence 1/1
If you have finished everything else and have spare time in the lab you could:
Check one of your results against the literature, or
Do an extra calculation on another small molecule, or
Do some deeper analysis on your results so far
You calculated and analysed HCN well done!