Rep:Mod:xo213

Introduction

The transition state of a reaction remains attractive to all chemists. It can not be obtained by any spectroscopic method since the corresponding lifetime of the transit state is small. The computational optimisation with GaussView provide a efficient way of analysing the transition state by calculating the molecular orbital interactions and steric interactions under various level of theories. Optimisation was carried out for the transition states of the Cope rearrangement, the Diels Alder reaction between cis-butadiene and ethene and the Diels Alder reaction between maleic anhydride and cyclohexa-1,3-diene.

Three levels of theories were applied in the optimisation, frequency analysis and IRC study: semi-empirical/AM1, HF/3-21G and B3LYP/6-31G(d). The semi-empirical method uses a minima basic set and Hamiltonian. To allow for rapid calculation, the calculation of core electrons is replaced by approximated values. The semi-empirical method is computationally cheap and therefore widely used in generating a crude structure of the molecule in study. The Hartree-Fock method also uses Hamiltonian but treat multiply electron system as a matrix of single electron wave functions. The salvation of matrix using slater determination results in the HF method computationally expensive. The B3LYP method treats multiple electron system as electron density functions at ground state which is less expensive but still accurate due to the application of low density approximation.

Nf710 (talk) 10:56, 16 December 2015 (UTC) Fairly good understanding of the background theory of the computational methods. and good referencing also. good intro

The Cope Rearrangement

The [3+3]-sigmatropic rearrangement is a pericyclic reaction involving the intramolecular shift of position of a σ bond. The reaction occurs in a concerted mechanism and both 'chair' and 'boat' configurations are considered to be possible in the transition state.

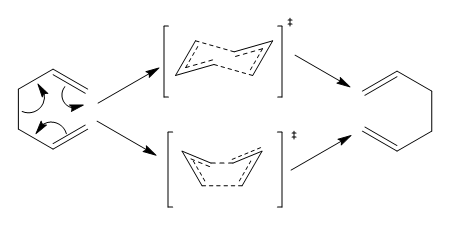
Scheme 1. the Cope Rearrangement Reaction Mechanism and Transition States

Conformation Study of Product and Reactant

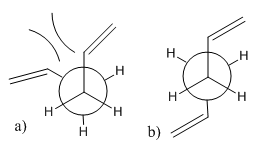
Both conformations of 1,5-hexandiene with gauche and anti-periplanar geometry in the middle 4 carbons were optimised with HF/3-21G method. By comparing the conformations and point groups with the list of low energy conformations, the calculated structures are associated with anti1 and gauche4 respectively. The calculated results follows the chemical intuition that the anti-periplanar tructure is more stable than the gauche structure from a steric point of view. As indicated on scheme 2 a), the alkene groups are close to each other which is sterically disfavoured and attribute to rise the energy of the gauche conformation. In the anti-periplanar conformation (Scheme 2 b), steric clash is minimised by placing two terminal alkenes farthest away from each other.

Scheme 2. a) Gauche conformer of butadiene b) Anti-periplanar conformer of butadiene

Nf710 (talk) 10:58, 16 December 2015 (UTC) Nice use of newman projections

However, repeating the optimisation of gauche structure with slightly twisted structure results in gauche3 conformer with point group of C₁ which is the energetically most stable conformer. The deviation from the previous chemical intuition implies the overall stablisation of the gauche3 structure is not resulted from pure steric factor. By visualising the HOMO of the gauche3 conformer in table 1, a strong π_C-C-π_C-C interaction between two terminal double bond and π_C-C-σ_C-H between alkene and neighbouring C-H bond are observed which attribute to the overall stablisation of 1,5-hexandiene structure. The stereoelectronic interaction is not involved in the case of gauche4 conformation and only π_C-C-σ_C-H interaction is involved in the case of anti1 conformer.

Conformation	Structure	Point Group	Energy/Hartrees HF/3-21G	HOMO
anti		C2	-231.69260235
gauche		C1	-231.69153031
gauche3		C1	-231.69266121

Table 1. Optimised conformations with point group, total energy and HOMO visualisations

Nf710 (talk) 11:00, 16 December 2015 (UTC) Excellent use of the oribitals to explain the relative energy! well done!

To obtain the energy of the 1,5-hexandiene bare the transition state, the anti2 conformer was optimised with HF/3-21G and followed by the B3LYP/6-31G(d) method. The geometry of the molecule changed by increasing the level of theory with the point group remaining C_i. Both C₄-C₉ and C₁-C₇ bond decreased while the C₄-C₁ bond increased as indicated on table 2. The descent in H-C-H angle also illustrated the variation in geometry. The small difference in the geometry and energy between two level of theories suggested the effectiveness and accuracy of the HF/3-21G method in rapid analysis of small molecular system.

level of theory	structure	energy	C4-C9 distance /a.u.	C1-C7 distance /a.u.	C1-C4 distance /a.u.	H-C-H angle /°
HF/3-21G		-231.69253521	1.50900	1.50900	1.55293	107.702
B3LYP/6-31G(d)		-234.61171063	1.50419	1.50419	1.54816	106.652

Table 2. Summary of energy and geometry information of anti2 conformer in HF/3-21G and B3LYP/6-31G(d) theory

Frequency calculation on the previous constructed B3LYP/6-31Gd anti2 conformer was then carried out for visualisation of the vibrational modes and thermochemistry. All the vibrational modes are associated with positive frequencies indicating that the optimisations with HF/3-21G and B3LYP/6-31Gd were successful to give a structure with local minimum energy.

Entry	Energy Type	Energy /Hartrees
1	Sum of electronic and zero-point Energies	-234.469219
2	Sum of electronic and thermal Energies	-234.461869
3	Sum of electronic and thermal Enthalpies	-234.460925
4	Sum of electronic and thermal Free Energies	-234.500809

Table 3. Thermochemistry information of anti2 conformer in B3LYP/6-31G(d) theory

The energies associated with the frequency calculation are included in table 3. The entry 1 indicates the total potential energy of the molecule at 0 K and only electronic and zero-point energy are included. The second entry is associated with the total energy of the molecule at 298.15 K and 1 atm. In this case, electronic, vibrational, rotational and translational motion are all included which gives a energy value higher than the entry 1. The energy in third entry involves the energy from entry 2 and additional contribution from RT, leading to the sum of electronic energy and enthalpic contribution. The entry 4 includes the entropic contribution to the total energy of the molecule.

Nf710 (talk) 11:02, 16 December 2015 (UTC) You have the correct energies here however you could have looked at the dihedral angles in the geom comparison.

Transition State Analysis

'Chair' Transition State Optimisation

Since the product and the reactant of the Cope rearrangement are the same in structure and of high symmetry, the transition state is expected to be highly symmetric and therefore, the 'chair' transition state was optimised using guess structure. The guess structure was constructed with two allylic fragments which were pre-optimised to minimum state using HF/3-21G method (Scheme 3). The separation between the terminal ends of the two allylic fragments was set to 2.2 A.

Scheme 3. Guessed chair structure

Two calculation methods were carried out to optimise the 'chair' transition state. The first method involves direct optimisation and frequency calculation using QS(berny) method with force constant being calculated once. Additional keyword 'Opt=NoEigen' was included to prevent the generation of multiple imaginary frequencies.

The second method utilised the frozen coordinate method. The pre-optimised guess structure was optimised again with the distance between terminal carbons of two allylic fragments frozen at 2.2 A. The additional keywords 'Opt=ModRedundant' was included in the optimisation. After the optimisation was completed, the resulting structure was re-optimised to a transition state with the same additional keywords included as in previous optimization. The previous frozen bonds were set as derivative to calculate force constant by differentiation along the reaction coordinate.

Method of Optimisation	Structure of Transition State	Energy of Transition State/Hartrees	Imaginary Frequency/ cm-1	Imaginary Frequency Animation
Direct Optimisation (HF/3-21G)		-231.61932247	-817.91
Frozen Coordinate (HF/3-21G)		-231.61932196	-817.99

Table 3. Summary of energies and imaginary frequencies of chair transition state

As indicated on the table above, similar energies of transition state and imaginary frequencies are given by using direct optimisation and frozen coordinate method with the same point group of C_2h. This observation indicates the guess structure is close to the real structure of the transition state which allows both methods being applied with high accuracy.

The imaginary frequency is calculated from the second derivative of the minimum energy of the molecule. In one dimensional quantum harmonic oscillator, the equation of frequency includes a term of (k/m)^1/2 where k is the force constant. The force constant resulted from the imaginary frequency is therefore associated with the vibration of the transition state.

The animation of the imaginary frequency provided the expected transformation between the product and reactant. While the terminal carbons on one side of two allylic fragments approaches (i.e. C₃ and C₁₄), the other two terminal carbons are moving away from each other. The distances of C1-C5 and C9-C11 decreases at the same time, implying the formation of a double bond during the transition state.

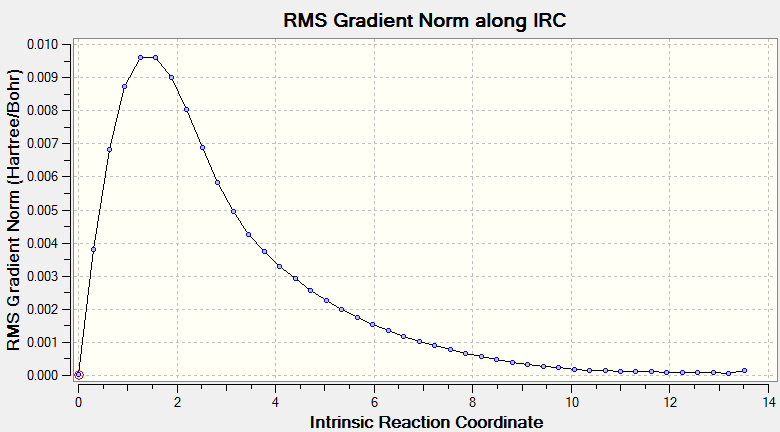
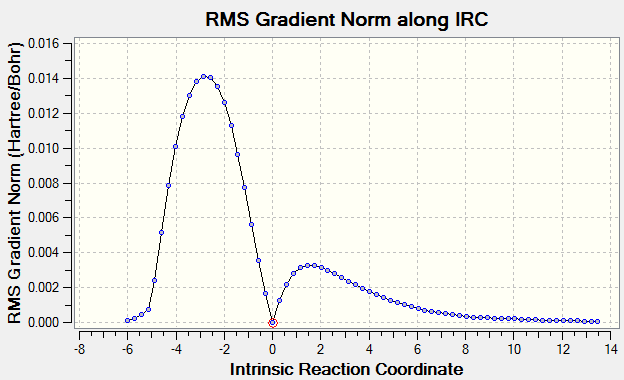
The Intrinsic Reaction Coordinate method was then carried out for the 'chair' transitions state from frozen coordinate method to find the local minimum. The total energy along IRC and RMS gradient norm along IRC are plotted separated as in Scheme 4 and 5. The total energy decrease from -231.619 to -231. 692 hartrees with the RMS gradient dropping close to 0, indicating the product is obtained successfully as the reaction coordinate moving away from the transition state.

Scheme 4. Total energy along IRC in the chair transition state

Scheme 5. RMS along IRC in the transition state

'Boat' Transition State Optimisaiton

The 'boat' transition state was optimised using the pre-optimised structure 'anti2' from previous section with QST2 method in HF/3-21G theory. Initially, the calculation was carried out without modification of the reactant and product and resulted in failure which suggested the QST2 method requires the structure of reactant and product to be close to the transition state. The calculation was then set up with specified structure and geometry of both reactant and product. The carbons on the anti2 structure are numbered accordingly and the geometry of the molecule is forced to Ci as in Scheme 6. The optimisation was proceeded successfully and the results summarised below.

Scheme 6 Reactant (left) and Product (reactant) used in 'boat' transition state optimisation

Structure of Transition State	Energy of Transition State/Hartrees	Imaginary Frequency/ cm-1	Imaginary Frequency Animation
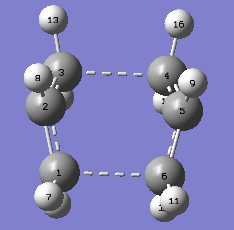
	-231.60280224	-840.22

Table 4. Summary of energy and imaginary frequency of boat transition state The animation of the 'boat' transition state gave a vibrational mode similar to the one obtained from the 'chair' transition state but in different point group (C_2v for boat shape). The decrease in the separation between C₁ and C₅ results in the crease in the C₃-C₄ bond length. The C₄-C₅ and C₂-C₃ bond lengths also decreases at the same time, implying bond order is changing from 1 to 2.

Nf710 (talk) 11:43, 17 December 2015 (UTC) All your frequencies are correct here and energies. Good understanding of how the TS optimisation working and why it is an imaginary frequencies. you didn't figure out which conformer it connects however, which you could have down by optimising down the last point on the IRC and comparing the energy twith the appendix, or calculated the IRC with force constants at every step.

B3LYP/6-31G(d) Optimisation of 'Chair' and 'Boat' Transition State

Both 'boat' and 'chair' transition states were re-optimised with B3LYP/6-31G(d) method using the structures from HF/3-21G method. All the electronic energies, sum of electronic and zero-point energies and sum of electronic and thermal energies are included in the table below. To calculate the activation energy under different level of theories, the energies of anti2 structure from direct optimisation method are also included.

The activation energy via chair transition state is much lower than the value via boat transition state in both HF/3-21G and B3LYP/6-31G(d) method, implying that the 'chair' transition state is more energetically favored in the real experiment. The results obtained from B3lYP/631G(d) method are closer to the literature value, which illustrated the efficiency and accuracy of re-optimisation of lower level theory to a higher level theory.

Summary of energies (in hartree)

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.61932247	-231.466700	-231.461341	-234.55693104	-234.414908	-234.408980
Boat TS	-231.60280224	-231.450930	-231.445302	-234.54307818	-234.402349	-234.396006
Reactant (anti2)	-231.69253521	-231.539543	-231.532567	-234.61171022	-234.469220	-234.461869

Summary of activation energies (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.71	44.69	34.08	33.18	33.3
ΔE (Boat)	55.61	54.76	41.96	41.33	44.7

Nf710 (talk) 14:01, 17 December 2015 (UTC) Your energies are very very good welldone, however you did not not compare the geoms of the different levels of theorey and therefore didnt come to the conclusion that lower basis sets are still very good at working out the geoms. you also could have compared your work to theory in more detail and given more detail about the discrepancies. You could have shown a better understanding of the theory, but in general this a well done report.

Appendix

Anti_HF/3-21G

Gauche_HF/3-21G

Gauche3_HF/3-21G

Anti2_HF/3-21G

Anti2_B3LYP/6-31G(d)

Chair_TS_HF/3-21G_direct_optimisation

Chair_TS_HF/3-21G_frozen_coordinate

Chair_TS_HF/3-21G_frozen_coordinate_IRC

Boat_TS_HF/3-21G_QST2

Chair_TS_6-31G(d)

The Diels Alder Reaction

The Diels Alder reaction is a concerted [4+2] cycloaddition process which is resulted from the molecular orbital interaction between a π⁴ component and a π² composent. During the reaction, 2 new σ bonds are formed. The molecular orbital interaction between reactants is studied with the reaction between the ethene and cis-butadiene (Scheme 7). The regioselectivity of the Diels Alder reaction is studied using cyclohexa-1,3-diene and malice anhydride as reactants (Scheme 8).

(What are the symmetry requirements for a Diels-Alder reaction? Tam10 (talk) 12:50, 10 December 2015 (UTC))

Scheme 7 Reaction scheme for Diels Alder reaction between cis-butadiene and ethene

Scheme 8 Reaction scheme for Diels Alder reaction between maleic anhydride and buta-1,3-diene

Molecular Orbital Interaction of the Diels Alder Reaction

The cis-butadiene and ethene are optimised using semi-emperical/AM1 method which was followed by re-optimisation at B3LYP/6-31G(d) level. The results from B3LYP/6-31G(d) calculation are included in the table below.

(Well done putting in the extra effort to compare AM1 to B3LYP Tam10 (talk) 12:50, 10 December 2015 (UTC))

Structure	Energy/Hartrees	HOMO Structure	LUMO Structure
	-155.98595181
	-78.58745744

Table 5 The energies, HOMO and LUMO strucure of the reactants

The calculated HOMO of cis-butadiene and LUMO of ethene are both anti-symmetric while the LUMO of cis-butadiene and HOMO of ethene are both symmetric. This observation confirmed with the fact that the cycloaddition reaction is resulted from the molecular orbital overlap between the HOMO-LUMO pair.

Scheme 9 Guessed structure of the transition state of the Diels Alder reaction between cis-butadiene and ethene

The transition state of the cycloaddition was optimised directly with the guess structure constructed from bicycle[2,2,2]octane as shown in Scheme 9. The carbons on the ethene component was placed 2.2 Å away from the terminal carbons on the cis-butadiene component with the double bond being set to 1.3 A to indicate the double bond property. The guess structure was optimised to transition state with QS(Benry) method and semi-emperical/AM1 and followed re-optimisation with QS(Berny) method and B3LYP/6-31G(d). The results from both semi-empirical/AM1 and B3LYP/6-31G(d) are included in the tables below.

Level of theory	Imaginary Frequency/cm-1	Imaginary Frequency Animation	First Positive Frequency Animation
Semi-emperical/AM1	-956.08
B3LYP/6-31G(d)	-525.34

Table 6. The imaginary frequencies of the optimised transition states under different level of theories

The animation of the imaginary frequency gives similar transformation as expected for transition state of the [4+2]-cycloaddition. As terminal carbons of butadiene and ethene comment approach each other, the bond length of the ethene component increases, indicating the transformation from a double bond to a single bond during the reaction. The bond length between the two middle carbon of the cis-butadiene component decreases to give a pseudo-double bond structure. Overall, the formation of two new C-C bond is synchronous. However, the imaginary frequencies and the energy from two optimizations are significantly different.

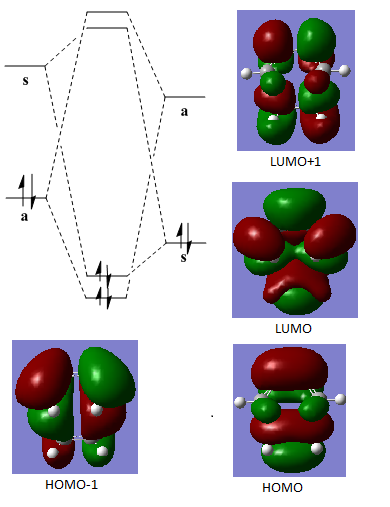
Since the cis-butadiene is lower in energy and electron-richer than ethene. Both the HOMO of the resulting transition state and the product are expected to be produced by the interaction between the HOMO of the cis-butadiene and the LUMO of the ethene component with anti-symmetric property. The generated HOMO and LUMO structures in the table below shows that the HOMO of the transition state from B3LYP/6-31G(d) optimisation is symmetric and resulted from the combination of the HOMO of ethene and LUMO of cis-butadiene which is deviated from the prediction.

The change in symmetry of the HOMO of the transition state can be explained by considering the energy of HOMO and HOMO-1 level (Scheme 10). The energy difference between HOMO and HOMO-1 level of the transition state is small. The optimisation from semi-empirical/AM1 method to B3LYP/6-31G(d) method is attribute to change the energy of the HOMO and LUMO since the semi-empirical/AM1 ignored the electronic interaction while B3LYP/6-31G(d) used electron density function for electronic interaction. Therefore, symmetric HOMO is observed in the case of B3LYP/6-31G(d) optimised transition state.

Scheme 10. HOMO-LUMO interaction in the optimisaiton in B3LYP/6-31G(d)

Level of theory	Energy/Hartrees	Structure of TS	HOMO Structure	LUMO Structure
Semi-emperical/AM1	0.11165466
B3LYP/6-31G(d)	-234.54389644

Table 7 The energy, HOMO and LUMO of the optimised transition states under different level of theories

The C(sp³)-C(sp³) bond, C(sp²)-C(sp²) and Van der Waal's radius of carbon are 1.54, 1.34 and 1.70 Å respectvely. The C₁-C₄, C₃-C₄ and C7-C10 bonds are all smaller than typical C-C single bond length and greater than the C=C bond length. This indicates the resonance of electron density across all the C-C bond in the transition state. The separation between terminal carbons of two component (C₃-C₁₀ and C₂-C₇) are larger than C-C single bond length but smaller than twice the Van der Waal's radii value which suggesting the potential formation of C-C bond across the terminal carbons.

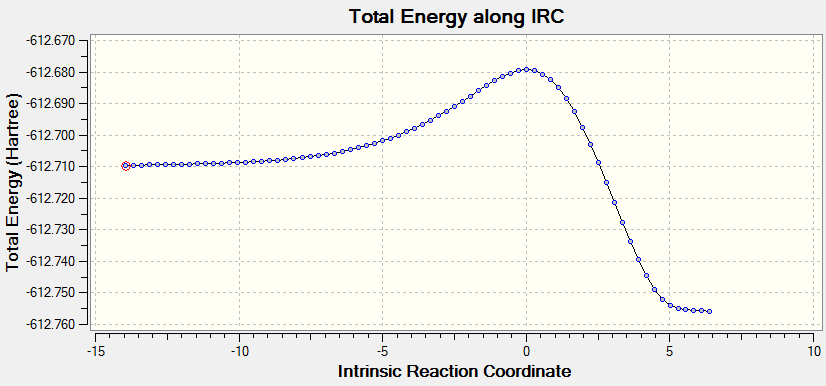
The IRC of the transition state was calculated in two directions. The RMS gradient norm reaches 0, implying the correct transition state was obtained.

Level of theory	C1-C2 length/a.u.	C1-C4 length/a.u.	C3-C4 length/a.u.	C3-C10 length/a.u.	C7-C10 length/a.u.
Semi-emperical/AM1	1.38186	1.39748	1.38186	2.11934	1.38294
B3LYP/6-31G(d)	1.38308	1.40720	1.38308	2.27208	1.38608

Table 8The summary of bond lengths in the transition states in semi-empirical and B3LYP/6-31G(d) theories

Scheme 11. the total energy along the IRC calculated in both direction

Scheme 12. the RMS along the IRC in both direction

Regioselectivity of Diels Alder Reaction

The Diels Alder reaction between cyclohexa-1,3-diene and maleic anhydride will lead to formation of both exo and endo product depending on how the molecular orbitals of two reactants overlap in the reaction pathway. The formation of endo product dominates under kinetic control. To study the regioselectivity of the Diels Alder reaction, the transition state of cycloaddition of maleic anhydride and cyclohexane-1,3-diene was optimised.

The transition states of both exo and endo product formation were optimised using QS(Berny) method and B3LYP/6-31G(d). The guess structures were constructed from the exo and endo product respectively which were pre-optimised to minimum energy by semi-empirical/AM1 followed by B3LYP/6-31G(d) method.

The energy, structure, HOMO and LUMO of the reactants and products in B3LYP/6-31G(d) theory are included in the table below.

Molecule	Structure	Total Energy /Hartrees	HOMO structure	LUMO structure
Cyclohexa-1,3-diene		-233.41893226
Maleic Anhydride		-379.28953484
Exo cycloadduct		-612.75578545
Endo cycliadduct		-612.75828993

Table 9. The energy, HOMO and LUMO strucures of reactants and products

The energies, imaginary frequencies and HOMO structure for both transition states are included in the table below. The endo transition state is lower in energy than the exo transition state. The presence of the steric clash between C-H bond on C₇ and C₁₀ and the maleic anhydride component (O=C-O-C=O) attributes to the rise in the energy of the exo transition state since C₇-C₂₀ separation is less than 2 X Van der Waal's radius of carbon. In the case of endo transition state, the through space separation between C₄ and C₁₉ is still small but both C₁ and C₄ are sp² hybridised with H(5)-C(1)-C(4)-H(6) plane parallel to the maleic anhydride component (O=C-O-C=O). The lack of steric interaction between cyclohexadiene and maleic anhydride components in the endo structure being less stained than exo transition state.

In the HOMO of the exo transition state, the orbitals on the O=C-O-C=O part is in the same phase with the orbitals on the double bond part which is potentially contributing to the through-space orbital interaction and therefore reduced the energy of the structure stereoelectronically. The similar though-space interaction between the orbitals on double bond and O=C-O-C=O is also observed on the HOMO of endo transition state. But the separation between the orbitals on the double bond and maleic anhydride is small which will lead to a stronger interaction and therefore stablise the endo transition state more than exo. This HOMO visulisaiton provided a MO approach to the secondary orbital overlapping effect in the transition state.

Transition State	Structure	Total Energy /Hartrees	Imaginary Frequency /cm-1	HOMO Structure
exo transition state		-612.67931096	-448.55
endo transition state		-612.68339678	-446.96

Table 10. The summary of the imaginary frequency, total energy, structures of HOMO and transition states

The animation of imaginary frequencies indicated the formation of two new σÅsigma bonds is synchronous in both endo and exo transition states. In endo transition state, the C1=C1 bond decreases in bond length while the pseudo single bonds( C₂-C₁₇ and C₃-C₁₅ ) are formed, implying the transformation from a single bond to a double bond. In the meantime, the C₁₅-C₁₇ decrease in bond length which suggests the bond order decreases from 2 to 1. The bond lengths in the transition state also provided a insight in the bond transformation.

In both transition states, the pseudo sigma bond length is longer than typical single C-C bond length but shorter than 2 X Van der Waal's radius of C which implies the potential formation of new C-C bond. The C₁-C₄, C₁-C₂, C₃-C₄ and C₁₅-C₁₇ distance are all close to 1.4 Å which suggests the presence of a resonance effect in the transition state which causes the separations to be longer than C-C single bond but shorter than C=C double bond.

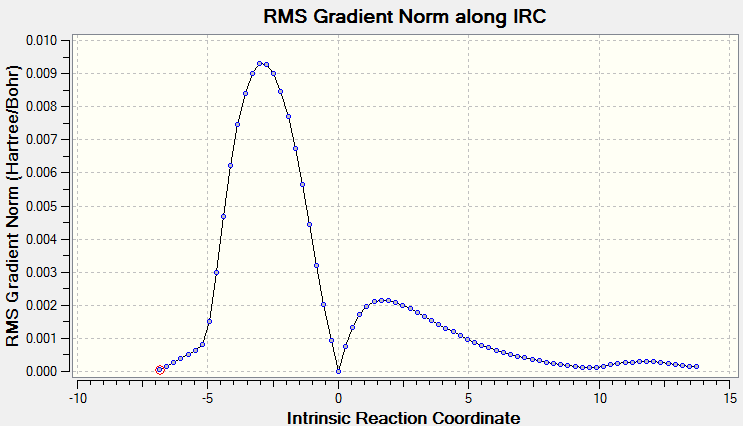
In the IRC analysis of both transition states, the RMS gradient drops to zero indicating the correct endo and exo transition states are optimised.

Transition State	c1-c4 length/a.u.	c15-c17 length/a.u.	c1-c2 length/a.u.	c3-c4 length/a.u.	pseudo C-C bond length/a.u.	Through Space C-C separation/a.u.
exo	1.40350	1.39785	1.39142	1.39142	2.29050	3.02815
endo	1.40309	1.39395	1.39125	1.39121	2.26826	2.99017

(This is a very good discussion. It seems you've put a lot of effort into bringing this all together Tam10 (talk) 12:50, 10 December 2015 (UTC))

Table 11. Summary of key bond lengths in the exo and endo transition states

Molecule	Sum of electronic and zero-point energies/Hartrees
Maleic Anhydride	-379.233651
Cyclohexa-1,3-diene	-233.296104
Exo Product	-612.569381
Endo Product	-612.572071
Exo transition state	-612.498013
Endo transition state	-612.502141

Table 12.Sum of electronic and zero-point energies of reactants, products and transition states

	Energy/ kcal mol-1
Activation Energy(exo)	19.92
Activation Energy(endo)	17.33
Reaction Energy(exo)	24.87
Reaction Energy(endo)	26.55

Table 13. Sum of activation energies and reaction energies in B3LYP/6-31G(d) theory

Scheme 13. Total energy along the IRC via the exo transition state

Scheme 14. RMS along the IRC via the exo transition state

Scheme 15. Total energy along the IRC via the endo transition state

Scheme 16. RMS along the IRC via the endo transition state

Appendix

butadiene_6-31G(d)

ethene_6-31G(d)

TS_between cis-butadiene and ethene at 6-31G(d)

TS_between cis-butadiene and ethene at AM1

cyclohexadiene_6-31G(d)

maleic_anhydride_6-31G(d)

exo_product_6-31G(d)

endo_product_6-31G(d)

exo_ts_6-31G(d) with IRC

endo_ts_6-31G(d) with IRC

Conclusion

Overall, the transition state of the Cope rearrangement and Diels Alder cycloaddition reactions were studied with three different optimisation method: i) direct optimisation from guess structure; 2) frozen coordinate method from guess structure; 3) QST2 method from twisted reactant and product structure. The study on the HOMO and LUMO of the Diels Alder reaction is then followed which provided a MO approach to the secondary orbital overlap effect which explains the regioselectivty.