Rep:Mod:xienzato123
Computational Lab: MODULE 1
From: Gabriele Uliana
Exercise 1 - Dimerisation of cyclopentadiene and hydrogenation of dicyclopentadiene
Dicyclopentadiene is an important chemical which undergoes a very rich chemistry. Its reactivity is dictated by the large strain present in the system and hence, it can easily react (often regioselectively) with hydrogen and other proton donors such as acids. When acid is used, in the appropriate conditions, dicyclopentadiene undergoes rearrangement reactions to produce an entirely different ring system 1. In this exercise, the exo and endo forms of dicyclopentadiene have been explored using molecular mechanics, followed by the reactivity of the endo form with hydrogen.
<font="5">Dimerisation of cyclopentadiene
The molecular mechanics program, MM2, was used to calculate the energy of the exo and endo dimers below in Fig.1
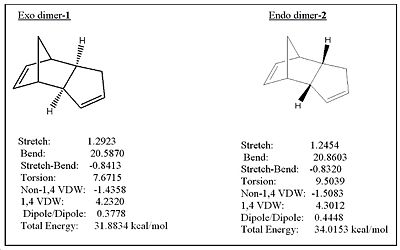
The endo dimer is thermodynamically less stable by approximately 2kcal/mol, since it has a higher total energy. The main contribution to this higher energy difference is due to torsional strain. However, it should be noted that the main contribution to the total energy of 1 and 2 is due to bending as a result of the bridgehead and the C=C bond in its vicinity. Despite the lower energy of the exo isomer, the endo isomer is formed instead! This is because we have to consider kinetics and hence transition state geometries which the MM2 program ignores. This implies that the activation energy for the endo isomer must be significantly lower than the exo product, overriding the thermodynamic factor. Hence, the dimerisation must be under kinetic control.
|
| ||||||
| Exo-Isomer | Endo-Isomer |
<font="5">Hydrogenation of dicyclopentadiene
MM2 was used to determine which hydrogenated form of 2 is thermodynamically more stable as depicted in fig.2
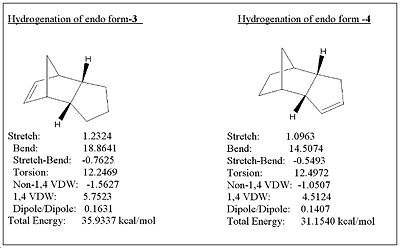
The results of the hydrogenation show that molecule 3 is thermodynamically less stable by approximately 5 kcal/mol, and is mostly attributed to the bending destabilisation and 1,4 VDW interactions which contribute to the higher energy of molecule 3. The extra bending destabilisation of 3 is due to the presence of the alkene near the already strained bridge head. If the hydrogenation was under thermodynamic control, then molecule 4 would be the major product formed in order to relieve some of the bending destabilisation. Since MM2 only gives data regarding thermodynamics, it isn’t enough to decide whether the kinetic contributions are enough to override the thermodynamics in order to favour the formation of 3 (as is the case with molecules 1 and 2). Information on the transition state geometries would be needed to make a conclusion as to which hydrogenated product would primarily form.
References
1. Herman Alexander Bruson, and Thomas W. Riener, The Chemistry of Dicyclopentadiene. I. Hydration and Rearrangement, J. Am. Chem. Soc.,1945, 67 (5), 723-728,DOI:10.1021/ja01221a009
Exercise 2 - Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)
In this exercise, MM2 was used to explain the stereochemistry of nucleophilic addition between two similar chemical reactions.
Reaction 1 - Mechanism

<font="5">Energy minimization of molecule 5

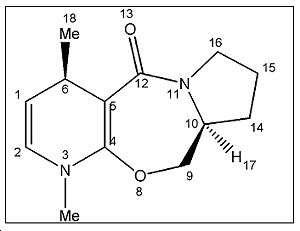
MM2 was done on molecule 5 to obtain a total energy of 26.3kcal/mol. The optimization procedure for the minimisation of energy involved altering the spatial arrangement of the atoms involved in the middle ring (atoms labelled 10,9,8,7 and 6) and running MM2 again. Altering the spatial position of the atoms and substituents on the aromatic ring system was of no use since the lowest energy geometry is fixed to be planar and made no difference to the total energy of the molecule. There was also no change in total energy when atoms 12, 13 and 14 were moved, indication that these substitutents didn’t have a significant influence on the energy change. However, when atoms 10 and 7 were stretched as shown in fig.3 the total energy of the molecule decreased to 25.72 kcal/mol.Further attempts were carried out, such as moving the carbonyl oxygen (11) and the nitrogen (9), but all gave higher energy conformations. The optimized structure for 5 is shown in jmol below.
Dihedral angle between atoms O11-C10-C4-C3 is 141o
optimizedmolecule5 |
<font="5">Energy minimization of molecule 6
MM2 was performed on molecule 6 to get an inital energy value of 28.87 kcal/mol. Atoms 12 and 9 were stretched in a similar fashion to molecule 5 (refer to fig.3). The procedure lowered the total energy of molecule 5, so it was assumed the same would be true for molecule 6. Indeed, this was observed and a lower energy of 28.34 kcal/mol was obtained. It should be noted that the product is thermodynamically less stable than molecule 5 by approximately 3 kcal/mol. This is expected due to the removal of the aromaticity present in molecule 5 and increased strain due to the introduction of the methyl group in molecule 6. Therefore, the reaction should be under kinetic control. The optimized jmol for molecule 6 is shown below.
optimizedmolecule6 |
<font="5">Conclusion for reaction 1
Complexation of the magnesium counter cation to the carbonyl oxygen produces a stabilised 6 membered transition state which directs nucleophilic attack of the methyl anion from the same face the carbonyl is pointing towards 2a (refer to jmol of molecule 5). Given that the carbonyl group is pointing out of the plane of the screen (towards you) in molecule 5, as evidenced by the dihedral angle value, the nucleophile will be oriented in such a way as to attack from the top face, opposite hydrogen 17, to produce the required stereochemistry shown in molecule 6. The stable 6 membered transition state indicates that the reaction is under kinetic control (the activation energy has decreased) since molecule 6 is thermodynamically less stable as a result of electronic repulsion due to the methyl group being in the same plane as the carbonyl.
Reaction 2 - Mechanism
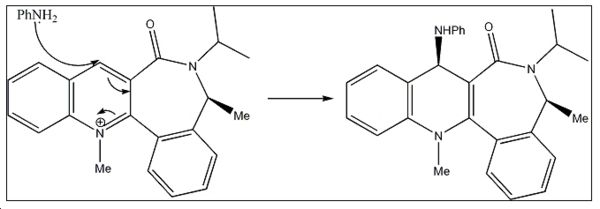
<font="5"> Energy minimization of molecule 7
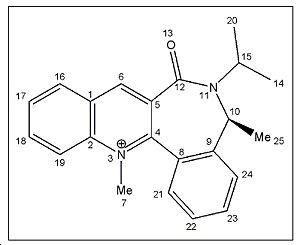
Initial energy obtained using MM2 is 32.5031 kcal/mol. Optimization was performed to get a lower energy value. Atom 12 was stretched as shown in fig.4 to give a lower energy conformation of 30.53 kcal/mol. Further alterations were made by changing the orientation of the isopropyl carbons (20,15,14), but higher energy conformations were obtained. However, it was noticed that when carbon atom 10 was stretched, a much lower energy conformation of 15.58kcal/mol was obtained! Optimized molecule 7 is shown in jmol below.
Dihedral angle between atoms O13-C12-C5-C4 = 133o
optimizedmolecule7-2 |
<font="5"> Energy minimization of molecule 8
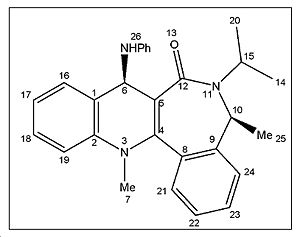
The initial energy obtained using MM2 was -7.0690 kcal/mol which cannot be right as a negative energy value doesnt make sense. In addition, the benzene rings are twisted and not planar as they should be. The problem resolved itself when moving the carbonyl carbon and oxygen and running MM2 again. The lowest energy geometry obtained has an energy value of 30.63kcal/mol and is represented in jmol below. The energy of molecule 8 is significantly higher than molecule 7 by approximately 15kcal/mol. This is expected since molecule 8 introduces the bulky -NHPh substituent which is in close proximity to methyl groups 20 and 25 (refer to labelled molecule 8 image) and hence the steric clash increases the total energy of the molecule. Therefore, this implies that the reaction must be under kinetic control.
optimizedmolecule8-2 |
<font="5">Conclusion for reaction 2
The orientation of the NHPh substituent in molecule 8 is due to the steric control of the carbonyl lactam 2b. The C3-C=O bond is the main contributor to the stereoselectivity of the nucleophilic addition. As can be seen from the jmol of molecule 7, the carbonyl group is pointing into the screen, in the opposite direction to the orientation of the methyl (25). Given that there is no stabilising complexation to the carbonyl, unlike in reaction 1, the bulky nucleophile attacks from the opposite face the electron rich C=O is facing, in order to minimise steric clash and produce the stereochemistry as shown in molecule 8.
References
2a. A. G. Shultz, L. Flood and J. P. Springer, J. Org. Chemistry, 1986, 51, 838. DOI:10.1021/jo00356a016
2b. Leleu, Stephane; Papamicael, Cyril; Marsais, Francis; Dupas, Georges; Levacher, Vincent. Tetrahedron: Asymmetry, 2004, 15, 3919-3928. DOI:10.1016/j.tetasy.2004.11.004
Exercise 3 - Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
Carbonyl addition depends on the relative stability of two intermediate isomers (isomer 10 and 11 discussed below) during the sysnthesis of taxol. In this exercise, MM2 is used once again to determine which isomer is most stable.
<font="5">Isomer 10

The initial energy obtained using MM2 was 175.998 kcal/mol where the cyclohexane ring adopted a high energy twist-boat conformation. The energy was optimized by altering the position of the carbonyl oxygen by stretching it away from the ring and varying its angle to eventually give a lower energy of 87.3 kcal/mol. The majority of the stabilisation was due to the lower bending energy. Upon further optimization, the lowest energy conformation of 41.8kcal/mol was obtained when atom C6 was moved out of position and the the twist-boat cyclohexane made to adopt the more stable chair conformation. The literature has the twist boat conformation listed as the most optimized form3, but I believe it to be incorrect since I have managed to successfully obtain the chair conformation. The structure of optimised 10 has the cyclohexane ring in a chair conformation with the carbonyl positioned on the same side as the methylene bridge C7 as shown in the jmol.
optimizedmolecule10GU |
<font="5">Isomer 11
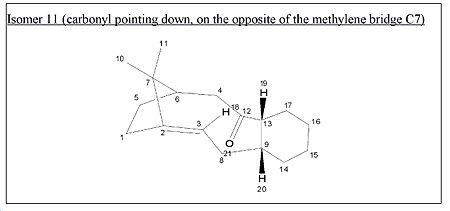
The initial energy obtained is 98.30 kcal/mol and is approximately 80kcal/mol lower than molecule 10 . This is mainly due to a much lower bending energy of molecule 11. Optimization was attempted in a similar fashion to molecule 10. The cyclohexane ring was changed from twist-boat to chair and this gave a lower energy of 90.7 kcal/mol which was expected. However, with further optimization, an even lower energy chair form was obtained with a total energy of 44.96kcal/mol. This was achieved by removing the hydrogens on the cyclohexane ring, doing a ring flip and performing MM2, restoring the hydrogens and then running MM2 again to get the final energy. This optimized structure has the cyclohexane ring in a chair conformation with the carbonyl positioned in the opposite direction to the methylene bridge, C7, as shown in the jmol below.
optimizedmolecule11GU |
<font="5">Conclusion
The energy of optimized molecule 11 is approximately 3kcal/mol higher in energy than optimized molecule 10. Most of that destabilisation energy is due to extra torsion and bending. Due to the relatively small energy difference of the isomers, it is quite difficult to compare and see where the extra torsion and bending is within isomer 11. The transannular carbonyl-hydrogen interactions were explored between 10 and 11, but that didn’t reveal much as both isomers had a very similar number of transannular interactions. Unfortunately, Chem3D doesn’t have the ability to tell the user where exactly the extra strain and torsion is located in the molecule. If time allowed, it would have been useful to explore more sophisticated software programs which give us that opportunity. Based on the thermodynamic data obtained, isomer 10 is responsible for the stereochemistry of carbonyl addition given that it is the more stable isomer.
<font="5">Why does the alkene in both isomers react slowly?
The reason why the alkene reacts slowly is because of its position adjacent to a bridgehead, and this makes it thermodynamically stable compared to other positional isomers4. It is important to note that this is only the case when the alkene is part of a large membered ring which contains more than about 7 atoms as Bredt's rules are not obeyed in this case. These alkenes are defined as 'hyperstable' and are relatively unreactive. This seems counterintuitive due to the large torsional strain expected compared with the optimal, planar alkene geometry; but this is alleviated when the alkene is part of a large membered ring, such as the taxol intermediates examined in this exercise.
References
3. S. W. Elmore and L. Paquette, Tetrahedron Letters, 1991, 319; DOI:10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0
4. Wilhelm F. Maier, and Paul Von Rague Schleyer, Evaluation and prediction of the stability of bridgehead olefins, J. Am. Chem. Soc., 1981, 103 (8), 1891-1900,DOI:10.1021/ja00398a003
Exercise 4 - How one might induce room temperature hydrolysis of a peptide
Two different reactions were considered involving a cis-decalin and a trans-decalin. The half life of hydrolysis for the cis-decalin reaction is much faster than the trans-decalin reaction. In this exercise, molecular modelling and kinetic arguments will be considered to explain this observation. The reactions that were studied are shown below in fig.5 (all energies were minimised using MM2 in this exercise)

In reaction 1 we are dealing with a cis-decalin while in reaction 2, a trans-decalin. Although both the cis and trans structures are under a significant amount of strain, both the alcohol and amide group don’t experience much steric compression between them which explains why the hydrolysis half life is much smaller than 500 years! For each decalin (cis and trans) there are two possible diastereoisomers which need to be considered. One has the ethylamido group equatorial, the other axial. The most stable isomer in each case will be the major reactant.
<font="5">Cis-decalin diastereomers

In each diastereoisomer, both rings were changed into chair conformations to obtain the lowest energy. The optimized energy for the equatorial ethylamido isomer is 17.2kcal/mol, where the lone pair of the alcohol is in close proximity to the amine hydrogen and hence H-bonding occurs to stabilise the structure. The optimized axial ethylamido isomer (both rings chair and H-bonding) has a total energy of 20.2 kcal/mol which is 3kcal/mol higher in energy than its equatorial counterpart. This is expected since axial substituents destabilise the structure as a result of syn diaxial interactions. The energy difference obtained of 3kcal/mol agrees well with the literature which states a value of 5.0kcal/mol5. Therefore, the major isomer for the cis-decalin is where the ethylamido group is equatorial as shown in jmol below.
| |||
| Cis-decalin with equatorial ethylamido group |
<font="5">Diastereoisomers of trans-decalin
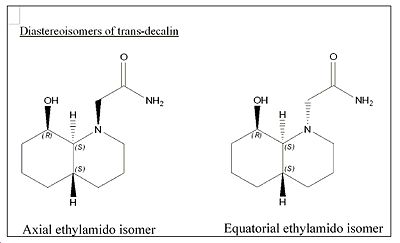
For the equatorial ethylamido isomer, the optimized energy was found to be 10.04kcal/mol. This diastereoisomer has a chair-chair conformation as well as having close proximity of the carbonyl oxygen with the hydroxyl group to allow for H-bonding stabilisation.
For the axial amide, the optimized energy was found to be 12.02kcal/mol. Again, the optimized structure consisting of chair-chair conformation and H-bonding stabilisation as mentioned before. Similar to the cis-decalin case, the axial amide is expected to be of higher energy due to the syn diaxial interactions. The energy difference obtained of approximately 2kcal/mol agrees very well with the literature value obtained of 3.1kcal/mol 5.
Therefore, the major conformer for the trans-decalin is where the ethylamido group is equatorial since it is lower in energy, as shown in jmol below.
| |||
| Trans-decalin with equatorial ethylamido group |
The table below summarizes the energies obtained for all the diastereomers. It shows that the energy of trans-decalin is lower than cis-decalin (for both the minor and major diastereomers). This is logical given that cis-decalins are under greater torsional strain. It can also be seen that the energy difference between the cis-decalin diastereomers is very similar to the energy difference in the trans-diastereisomers, coming in at 3kcal/mol and 1.98kcal/mol respectively.
| Cis-decalin major isomer (equatorial ethylamido) | 17.2 kcal/mol |
| Cis-decalin minor isomer (axial ethylamido) | 20.2 kcal/mol |
| Trans-decalin major isomer (equatorial ethylamido) | 10.04 kcal/mol |
| Trans-decalin minor isomer (axial ethylamido) | 12.02 kcal/mol |
<font="5">So… why does the cis-decalin hydrolyse much faster than the trans-decalin?
In order for intermolecular nucleophilic attack to occur, the hydroxyl group must be close enough to the amine and approach at the right trajectory. After having found the major diastereoisomer in each decalin, they had to be examined carefully to see why the cis-decalin reacts much faster than the trans-decalin.
|
Fig.6 Cis-decalin reaction scheme |

|
Fig.7 Trans-decalin reaction scheme |
By examining the cis-decalin reaction scheme in fig.6 , the equatorial ethylamido group (major isomer) is in the correct orientation to allow for intramolecular attack from the hydroxyl group. However, if we compare with the trans-decalin scheme in fig.7 Only the minor isomer, where the ethylamido group is axial, is in the right orientation to react successfully. Therefore, in order for the reaction to occur, the ethylamido group must first invert from equatorial to an axial orientation 5. This requires energy (exactly 1.98 kcal/mol which corresponds to the difference in energy between the diastereomers) and results in a higher activation barrier, and hence explains why the trans-decalin reacts significantly slower.
References
5. M. Fernandes, F. Fache, M. Rosen, P.-L. Nguyen, and D. E. Hansen, 'Rapid Cleavage of Unactivated, Unstrained Amide Bonds at Neutral pH', J. Org. Chem., 2008, 73, 6413–6416 ASAP: DOI:10.1021/jo800706y
Exercise 5 - Modelling using semi empirical molecular orbital theory
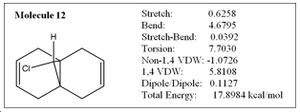
In this exercise, we have moved on from using a purely mechanical based method to a quantum based methodology. The regioselective addition of dichlorocarbene was explored using MM2 and the results compared with more sophisticated semi-empirical functions, which gave a graphical representation of the molecular orbitals in the molecule. In addition, particular stretching frequencies of the molecule were explored. MM2 was performed on molecule 12 below to obtain the optimized energy of 17.90 kcal/mol.
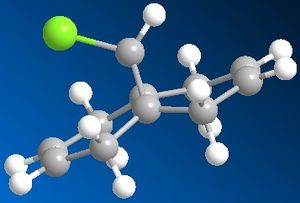
Next, the HF/STO-3G self-consistent-field MO method was used to obtain a graphical representation of the valence electron molecular wavefunctions. There was no noticeable change in the geometry compared with the MM2 minimised one which implies that the MM2 method obtained a very accurate, optimized geometry. The HOMO-1, HOMO,LUMO, LUMO+1, LUMO+2 molecular orbitals are shown below (isocontour set to 0.02).
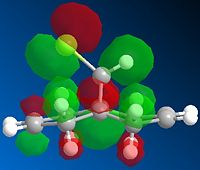 |
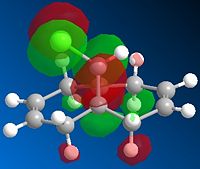 |
 |
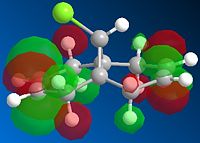 |
|
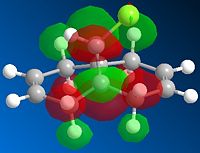
| HOMO-1 MO | HOMO MO | LUMO MO | LUMO+1 MO | LUMO+2 MO |
The HOMO corresponds to the endo C=C π orbital, the LUMO + 2 orbital corresponds to the C-Cl σ* orbital and the HOMO-1 corresponds to the exo C=C π orbital 6. The endo alkene is more nucleophilic than the exo alkene given that it has a greater pπ-orbital coefficient and hence a larger amount of electron density. This can be seen in the HOMO-1 molecular orbital where there is more electron density at the endo C=C compared with the exo C=C bond.
<font="5">Investing the C-Cl, and C=C stretching frequencies in molecule 12 and it’s hydrogenated form, molecule 13.
MM2 optimization was performed on molecule 13 below, which has the exo C=C bond hydrogenated:
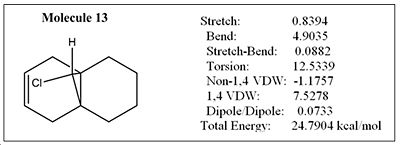
The geometry of 13 has been optimised, first using MM2. The energy obtained from MM2 was 24.79 kcal/mol. The cyclohexane ring adopts a 'pseudo' boat conformation as shown in fig.8 The cyclohexane ring geometry in molecule 13 couldn't be optimised any further since the conformation is locked as a result of the bridgehead at the ring fused carbons. It should also be mentioned that the energy of 13 is roughly 6kcal/mol higher than 12. This is because of higher torsional strain, most likely as a result of introducing extra hydrogens and hence increasing syn diaxial interactions. Molecule 13 was then further optimised by using the HF/STO-3G self-consistent-field MO method. Similarly with molecule 12, there was no noticeable change to the geometry of the molecule compared with the optimised one using just MM2.

Both the HF/STO-3G optimized .gjf files for molecules 12 and 13 were then sent to SCAN in order to obtain the IR data.
<font="5">Stretching frequencies for molecule 12
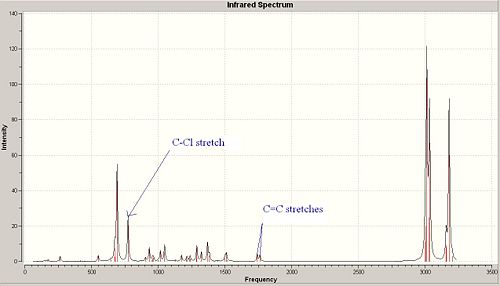
Molecule 12 has 69 different vibrational modes. There are various vibrational modes containing C-Cl stretches, so only the vibrational mode which contains the most noticeable stretch will be mentioned. This was judged by animating each particular vibrational mode on Gausswiew and deciding which C-Cl stretch was the most significant and gave the higest intensity. The most significant C-Cl stretch has a frequency of 772.63 cm-1 with an intensity of 25.2 and is labelled in the IR spectrum. Similarly with the C=C stretches, there are many vibrational modes which contain these, but the most significant stretches occur at 1740.76 cm-1 and 1760.91 cm-1 with an intensity of 4.14 and 3.90 respectively. Both stretches are labelled on the spectrum above. The intensity of the C-Cl stretch is much greater than the C=C stretch due to the greater change in dipole moment when the bond is stretched.
<font="5">Stretching frequencies for molecule 13
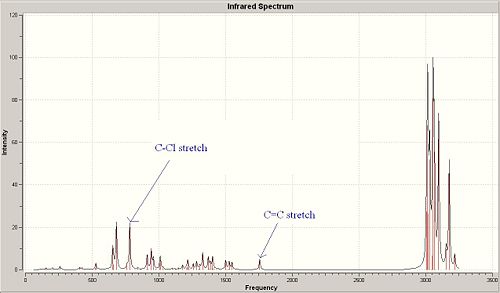
Molecule 13 has 75 different vibrational modes. In a similar manner to molecule 12, the vibrational modes containing the most significant C-Cl and C=C stretches have been identified. It was found that the most significant C-Cl stretch (which had the same animation as the one in molecule 12) occurred at 782.97 cm-1 with an intensity of 22.09; whilst the corresponding C=C stretch occurred at 1757.26 cm-1 with an intensity of 5.01. The C-Cl and C=C stretches are labelled on the IR spectrum.
<font="5">Why is the C-Cl stretching frequency larger in molecule 13 compared with 12?
In molecule 12, the exo C=C π orbital interacts with the C-Cl σ* 6. The interaction occurs since the σ* lobe points towards the exo C=C π bond and therefore, some degree of orbital overlap occurs. As a result, electron density is donated into the C-Cl σ* which weakens the bond and increases the bond length. Hence, the C-Cl stretching frequency is slightly smaller in molecule 12 as less energy is required to stretch the C-Cl bond since it's weakened. If the endo C=C bond was hydrogenated instead, it was predicted that the C-Cl stretching frequency would not change since orbital overlap between the endo C=C π and C-Cl σ* does not occur.
Published IR data for molecule 12
Published IR data for molecule 13
References
6. B. Halton, R. Boese and H. S. Rzepa., J. Chem. Soc., Perkin Trans 2, 1992, 447. DOI:10.1039/P29920000447
My own mini project: First total synthesis of 10a-hydroxy-4-muurolen-3-one and its C10-isomer
The following, overall reaction scheme in fig.9 by F.Q. Bi et al has been explored for this mini project: (please note that all the literature values listed in this mini project for the IR, optical rotation and 13C NMR have been obtained from reference 7.)
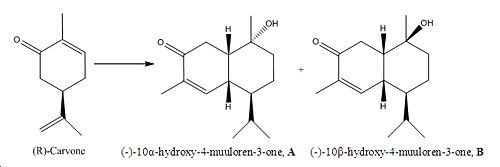
The two muuloren diastereoisomer derivatives, A and B are distributed as plant constituents 7. They have interesting structures which makes them very biologically active. In addition, B has shown antifungal activity against L. betulina. Also, both structures A and B are cis decalins! So part of the reason why this project was chosen was to do with the interesting resemblance with exercise 5. In this project, the IR, 13C NMR and optical rotation of A and B will be determined using computational techniques and compared to the results in the literature.
The energy of A and B had to be optimized before submitting to SCAN and calculating the spectra.
<font="5">Energy optimization of A and B
MM2 inital energy of A = 24.42kcal/mol where the hydroxyl is axial and the cyclohexane ring adopted a boat conformation. Changing the cyclohexane ring into a chair conformation (with the hydroxyl group now equatorial and methyl axial) gave the optimized energy of 18.41kcal/mol. For more accurate results, HF/STO-3G was used to get a more optimal geometry followed by DFT=mpw1pw91 method using 6-31G basis set. MM2 initial energy of B = 25.94 kcal/mol where the hydroxyl is equatorial and the cyclohexane ring adopting a boat conformation. Changing the cyclohexane ring into a chair conformation like before (with the hydroxyl now axial and methyl equatorial) gave the optimized energy of 18.28kcal/mol. For more accurate results, HF/STO-3G was then used to get a more optimal geometry followed by DFT=mpw1pw91 method using 6-31G basis set. The DFT optimized jmol of A and B are shown below.
| DFT=mpw1pw91, 6-31G optimized molecule A | DFT=mpw1pw91, 6-31G optimized molecule B |
<font="5">Comparison of the energies
The optimized geometry for both A and B appear to have very similar energies. This is logical since the only difference between them is due to the orientation of the methyl and hydroxyl. Both the methyl and hydroxyl are groups of similar size (methyl being slightly larger) which explains the similarity in the energy and why the energy of isomer B is lower by a small amount. The geometries of A and B have been optimised using the mpw1pw91/6-31(d,p) method before being sent off to SCAN to calculate the IR, NMR and optical rotation
<font="5">IR spectrum of A
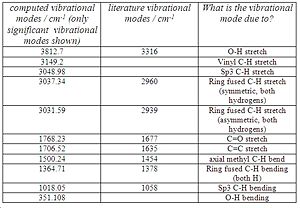
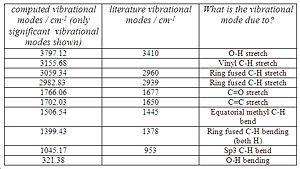
There are a total of 117 vibrational modes. The computed IR spectrum of molecule A and the table comparing the literature IR frequencies with the computed ones are shown below in fig.10 and 11 respectively.
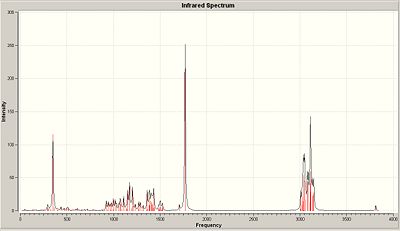
Unfortunately, the authors did not state what each vibrational frequency is responsible for, so they were matched with their corresponding, computed frequencies to the best of my knowledge (see fig. 11). The O-H stretches don’t match very well. This is expected due to the many interactions the O-H can take part in such as hydrogen bonding which the computational method might not take into account very well. Both ring fused C-H stretches match well with the computed value. However, the C=O and C=C computed stretches are both slightly higher than expected. This implies that the b3lyp/6-31G(d,p) method used to calculate the IR hasn’t taken the enone conjugation into account as that lowers the frequency of the C=C and C=O stretches. Assuming I have matched the frequencies correctly, the sp3 C-H bending , axial methyl C-H bending and ring fused C-H bending modes are in good agreement with the literature.
Link to the published IR data of molecule A:
<font="5">IR spectrum of B
Like molecule A, there are a total of 117 vibrational modes which was expected given the similarity between the diastereoisomers. The IR spectrum of molecule B and the table comparing the vibrational frequencies are shown below in Fig.12 and 13 respectively.
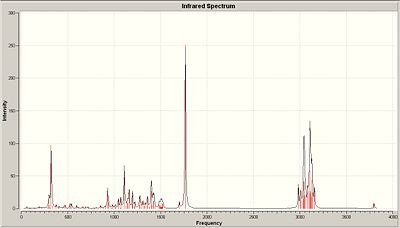
Comparison of the literature vibrational modes of B with those of molecule A show that there is very little difference between them. This is expected because the diastereoisomers are so similar in structure. However, the sp3 C-H bending and O-H stretch differ by a (relatively) significant amount between the literature values of A and B, so those stretches could be used to distinguish between the diastereomers. Interestingly, it was noticed that the ring fused C-H stretching modes are unique to A and B. When the ring fused C-H stretching modes were animated using Gaussview, molecule A’s consisted of both hydrogens stretching in a symmetric fashion in phase, or stretching antiphase in an asymmetric sense. These stretching modes were not observed in molecule B! Instead, the ring fused C-H stretching modes consisted of one of the hydrogens stretching at 3059.34 and then the other one at 2982.83. Overall, the literature vibrational modes for A and B seem to correspond well with the computed values obtained, which shows that the correct geometries for A and B have been obtained.
Link to the published IR data of molecule B:
Next, the 13C NMRs were computed using the GIAO method.
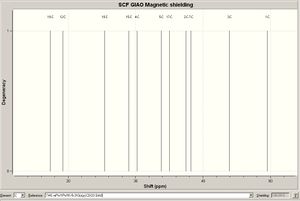
<font="5">Molecule A 13C NMR
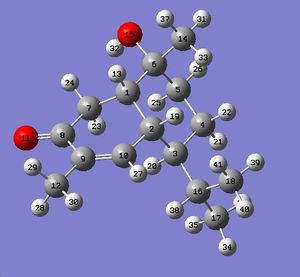
The images below reveal all the computed data obtained for molecule A, including a table which compares the literature chemical shifts to the computed ones.
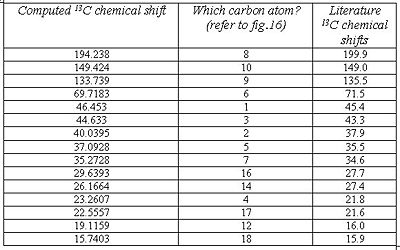
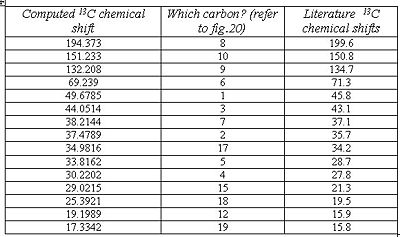
As can be seen from fig. 17, the computed chemical shifts match extremely well with the literature, where most values are within ca. +/-2ppm, hence confirming that the lowest energy conformation for the molecule has been obtained. The high accuracy of the computed values is due to the geometry of compound A being optimized to a very high level of accuracy using the mpw1pw91/6-31(d,p) method and basis set. The computed chemical shifts obtained are logical and make sense with respect to the structure being analysed. Carbon atoms 8, 10 and 9 involved in the enone conjugation are the most deshielded and so they have the largest chemical shifts.
Link to the published NMR data of molecule A:
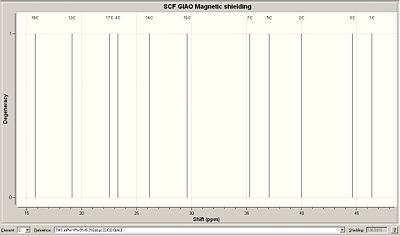
<font="5">Molecule B 13C NMR
The images below reveal all the computed data obtained for molecule B, including a table which compares the literature chemical shifts to the computed ones.
Note that Gaussian has labelled some carbon atoms differently in B compared with A
The literature values match reasonably well with the computed values, but the correlation is not as good compared with molecule A. Carbon atoms 5, 15 and 18 are quite far off from the literature which implies that the conformation hasn’t been optimized for these atoms. Given the similarity between molecules A and B, it doesn’t come as a surprise that the chemical shifts match so closely and hence it is difficult to differentiate between them. However, a surprising difference was noticed between the NMR of A and B which could be used to differentiate between them. Using the literature values, the difference in chemical shift between atom 17 in A and atom 18 in B (both the same atoms, just labelled differently by Gaussian) is the largest coming at 2.1ppm. Therefore, by observing the chemical shift of that particular atom, it could be possible to differentiate between the diastereoisomers. Unfortunately, the same ‘anomaly’ is not present using the computationally obtained chemical shifts. However, this is understandable given the accuracy of the computational technique used and high level of sensitivity required to be able to differentiate the diastereoisomers.
Link to the published NMR data of molecule B:
<font="5">Optical rotation of molecule A and B
The literature optical rotation for A is quoted as [α]D20=-98 while the computed value obtained came in at [α]D20=-150.60. There is a large difference between the values and this is expected since the optical rotation is highly dependent on concentration and temperature, which the computational method used doesn’t take into account. However, what’s important is that the absolute sign obtained matches with the literature value, which confirms that the authors have obtained the correct enantiomer.
The literature optical rotation for B is quoted as [α]D20=-100 while the computed value obtained is [α]D20=-51.04. The absolute value doesn’t match very well with the literature for the same reasons listed for molecule A. Due to the similarity of the diastereoisomers, and the relatively low accuracy of the method used for the optical rotation, it isn’t surprising to see that there is no correlation between the values obtained with the literature. However, the absolute signs do match which is reassuring as it suggests that the authors have obtained the correct enantiomer.
Unfortunately, optical rotation cannot be used to distinguish between A and B since it is not accurate enough.


Links to the published optical rotation data for molecules A and B:
- Published optical rotation data for A
- Published optical rotation data for B
References
7. Fu Qiang Bi, Li Jing Fang, Chen Xi Zhang, Yu Lin Li, First total synthesis of 10a-hydroxy-4-muurolen-3-one and its C10-isomer, Chinese Chemical Letters, 19, (2008), 1265–1267 DOI:10.1016/j.cclet.2008.09.022
Conclusion for module 1
In the beginning of module 1, the method of molecular mechanics was used to obtain the optimum geometry. This method, however, was outparsed by the more accurate and reliable Hartree-Fock method which took into account the quantum nature of electrons. Both the MM2 and HF methods were used in exercise 5 and the mini project to optimize the geometry of various molecules in order to explain chemical reactivity. This was taken further by obtaining electron density surfaces which were used to explain interesting phenomena regarding the variation in stretching frequency of a particular bond in different isomers (see exercise 5).
Using the techniques learned from previous exercises, an interesting mini project was chosen, which consisted of the characterisation of two cis-decalin diastereoisomers. The IR, NMR and optical rotation for both isomers were computed and compared with the literature values. Although the IR and NMR values obtained matched well with the literature, the optical rotation did not; but this is due to the limitation of the computational technique used. Overall, the mini project was successful and confirmed that the correct geometry for both diastereoisomers were obtained.