Rep:Mod:xangy123
Alexandre Ferreira's Molecular Modelling 2 Wiki Page!
Welcome to Alexandre Ferreira Molecular Modelling 2 Wiki Page!
Ammonia
Ammonia Basic Information
A molecule of ammonia was constructed in Guassview and a Gaussian calculation was run, determining optimum geometry and bond lengths for the molecule, as well as molecular orbitals and vibrational data. identical optimization procedured were performed on Nitrogen, Hydrogen and Fluorine, which are shown below.
Name: Ammonia
Calculation Method: RB3LYP
Basis Set:6-31G(d,p)
Final Energy:-56.558
RMS Gradient:0.00000485
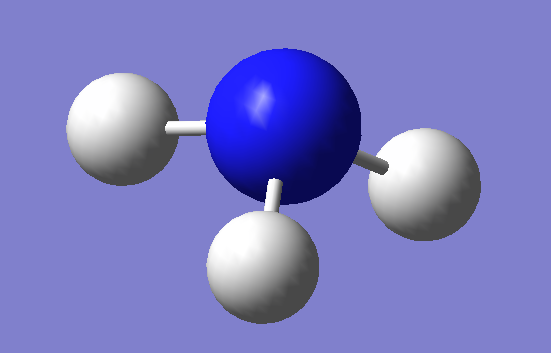
Point Group:C3V
N-H bond length: 1.02 A
The table below shows the results of the optimization. the table shows the force acting on the atoms of the molecule. force is the first derivative of potential energy, so the closer the force is to 0, the closer the potential energy is to a stationary point (a minimum)
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES Predicted change in Energy=-5.986276D-10
Optimized Structure
Log File For Ammonia
Interactive Model of molecule
test molecule |
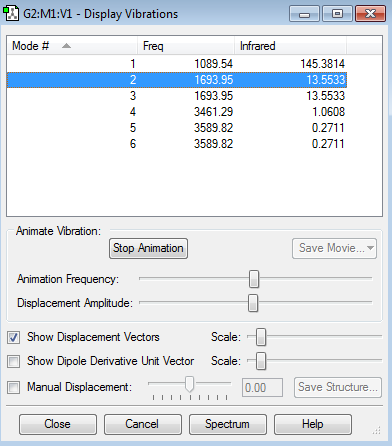
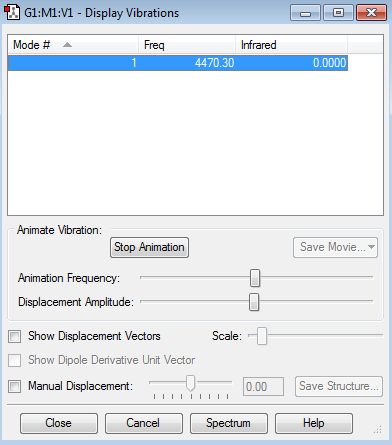
Vibrational Nodes
6 nodes expected
2 sets of degenerate modes (modes 2 and 3, and modes 5 and 6)
4 sets of degenerate nodes, 4 expected absorptions on spectra
Mode 1- Bending (umbrella node) Modes 2 and 3- Bending Mode 4- Stretching Modes 5 and 6- Stretching
Ammonia Vibration Data Screenshot
Charge Distribution Data
Nitrogen Has charge of -1.125, each hydrogen has charge of 0.375. this is expected as nitrogen is more electronegative than hydrogen.
Nitrogen
Nitrogen Basic Information
Name: Nitrogen
Calculation Method: RB3LYP
Basis Set:6-31G(d,p)
Final Energy:-109.52
RMS Gradient:0.00000097
Point Group:DinfH
N-N bond length:1.106A
Item Value Threshold Converged? Maximum Force 0.000002 0.000450 YES RMS Force 0.000002 0.000300 YES Maximum Displacement 0.000001 0.001800 YES RMS Displacement 0.000001 0.001200 YES Predicted change in Energy=-8.782393D-13
Optimized Structure
Log File For Nitrogen
Interactive Model of Molecule
test molecule |
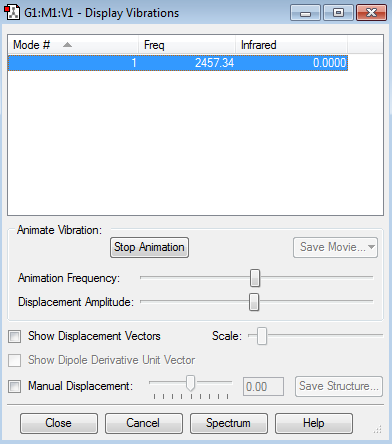
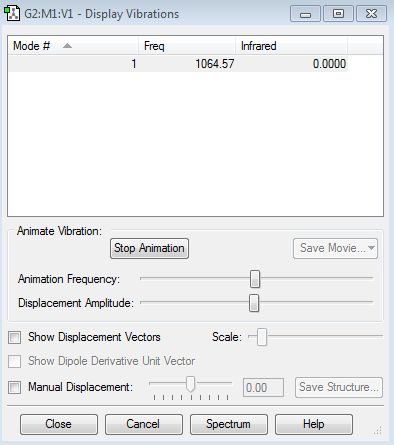
Vibrational Nodes
1 stretching mode expected, so 1 absorption reading in an IR spectra is expected
Nitrogen Vibrational Data Screenshot
Charge Distribution Data
Nitrogen is a neutral homonuclear diatomic molecule, so there is no dipole and there is a perfectly even charge distribution
Hydrogen
Hydrogen Basic Information
Name: Hydrogen
Calculation Method: RB3LYP
Basis Set:6-31G(d,p)
Final Energy:-1.18
RMS Gradient:0.00013
Point Group:DinfH
H-H bond length: 0.742
Item Value Threshold Converged? Maximum Force 0.000232 0.000450 YES RMS Force 0.000232 0.000300 YES Maximum Displacement 0.000305 0.001800 YES RMS Displacement 0.000431 0.001200 YES Predicted change in Energy=-7.091616D-08
Optimized Structure
Log File For Hydrogen
Interactive Model of Molecule
test molecule |
Vibrational Nodes
1 stretching mode expected, so 1 absorption reading in an IR spectra is expected
Hydrogen Vibrational Data Screenshot
Charge Distribution Data
Hydrogen is a neutral homonuclear diatomic molecule, so there is no dipole and there is a perfectly even charge distribution
Reaction Energy Calculation
2 molecules of nitrogen and 6 molecules of hydrogen react to create 2 molecules of ammonia. using these stoichiometric ratios and the energy of the molecules yielded by the optimization to calculated the change in energy of the reaction and thus determine whether the reactants or products are more stable.
Energy of hydrogen in au: -1.17853929
Energy of nitrogen in au: -109.52412868
Energy of ammonia in au: -56.55776873
Energy of Reactants: -113.05974655 au
Energy of Products: -113.11553746 au
Energy of reactants in kJ/mol:-296838.36
Energy of products in kJ/mol: -296984.84
Change in energy in kJ/mol:-146.48
Products (ammonia) is more stable than the reactants (nitrogen and hydrogen)
Analysis of a Fluorine Molecule
Fluorine Basic Information
Name: Fluorine
Calculation Method: RB3LYP
Basis Set:6-31G(d,p)
Final Energy:-199.50
RMS Gradient:0.00000070
Point Group:DinfH
F-F bond length:1.40
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000001 0.001800 YES RMS Displacement 0.000002 0.001200 YES Predicted change in Energy=-1.800054D-12
Optimized Structure
Log File For Fluorine
Interactive Model of Molecule
test molecule |
Vibrational Nodes
1 stretching mode expected, so 1 absorption reading in an IR spectra is expected
Fluorine Vibrational Data Screenshot
Charge Distribution Data
Fluorine is a neutral homonuclear diatomic molecule, so there is no dipole and there is a perfectly even charge distribution
Analysis of Select Molecular Orbitals
The orbital shown above is one of two identical π* antibonding orbitals formed by the 2p orbitals perpendicular to the internuclear axis (the 2p orbital paralel to the internuclear axis forms a σ orbital). these are important orbitals in fluorine as they an energy depth of -0.39au, the highest of any occupied orbital in fluorine, and are thus the Highest Occupied Molecular Orbitals (HOMO) in fluorine.
there are two of these orbitals because there are two 2p orbitals (2p_z and 2p_y, if the internuclear axis is defined as the x axis) which are perpendicular to the internuclear axis. the two orbitals are also perpendicular to each other (the three 2p orbitals are orthogonal to each other. the resulting molecular orbitals are degenerate and arranged perpendicularly to eachother, much like their constituent atomic orbitals.
The orbital shown above is the σ* antibonding orbital formed by the 2p orbitals parallel to the internuclear axis. this orbital is important in fluorine as it has an energy depth of -0.13au, the lowest of any unoccupied orbital, and thus is the lowest unoccupied molecular orbital (LUMO) in fluorine.
The orbital above is the σ bonding orbital formed by the 2s orbitals. this orbital has an energy depth of -1.34au, much lower than the orbitals discussed above.
The orbital above is the σ* antibonding orbital formed by the 2s orbitals. this orbital has an energy depth of -1.09au, much lower than the HOMO and LUMO orbitals discussed above.
The orbital above is the σ bonding orbital formed by the 1s orbitals. this orbital has an energy depth of -24.80au, much lower than all the orbitals discussed above, which range in energy depth from -0.13au to -1.34au). this characteristic of the orbital can be seen by how close it lies to the nuclei of the atoms relative to the other orbitals. unlike the orbitals above, this orbital has a principle quantum number of 1, which means that it does not contain valence electrons. the electrons in this orbital will never take part in any bonding.