Module 3

Through out this experiment the accuracy of the results can be improved by using various levels of theory. There are different degrees of theory accuracy, some types of theory take account of the vairational theory such as B3LYP DFT, MM2 and Coupled Cluster theory(whereby the repulsive interactions experienced between electrons is taken into account) and other methods do not take into account such interactions e.g. The Hartree Fock theory. However, the greater the 'detail' of the calculation , the more computationally demanding and expensive it is likely to be. Furthermore, the type of basis set can be modified to include an larger number of functions to better represent the behaviour of the system. In this investigation the basis set used for HF is 3-21G and for DFT B3LYP/6-31G*.

The Cope Rearrangement

The Cope rearrangement occurs via a[3,3]-sigmatropic shift rearrangement mechanism. It has been widely accepted that the reaction is concerted and goes via a "chair" or a "boat" transition structure, "boat" transition structure is thought to be higher in energy.

Optimizing the Reactants and Products

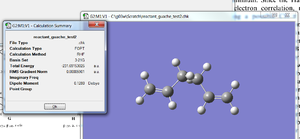
GaussView was used to draw a molecule of 1,5-hexadiene with an "anti" linkage for the central four C atoms. The structure was cleaned using the 'Clean' function in GaussView, this performs a force-field (molecular mechanics) minimization of the structure. The structure was optimized at the HF/3-21G level of theory and the % mem allocation was changed to 250 MB. Once the optimisation calculation was completed, the checkpoint file was opened and the total energy was found to be -231.692535 a.u. The structure was symmetrised and the assigned point group was Ci.

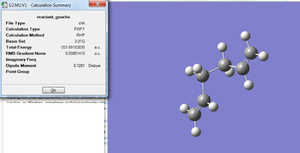
Next, another molecule of 1,5-hexadiene with a "gauche" linkage for the central four C atoms was created. The structure was optimised at the HF/3-21G level of theory and the final energy value was -231.6915303 a.u. The structure was symmetrised and the assigned point group was C2.

Since the calculated activation energies and enthalpies of structures general use the lowest energy conformation of a reactant molecule as a reference, several test structure of 1,5-hexadiene was created and energy optimisation calculations were run.

**Table 1: Various 1,5-Hexadiene conformations optimised at the HF/3-21G level of theory**
Structure	Point Group	Energy/ a.u.
Reactant Anti	Ci	-231.692535
Reactant Gauche	C2	-231.69153035
Reactant Gauche1	C2	-231.69153025
Reactant Gauche2	C1	-231.69266096
Reactant Gauche2	C2	-231.68771590

Table 1 (my computed results) shows the variations in energy of different 1,5-hexadiene conformations. The lowest energy conformer is the gauche 3 conformer (-231.69266096 a.u. point group C1) and the highest energy conformer is the gauche 4 conformer. According to the results in Appendix 1 gauche conformer 3 has the lowest energy -231.69266 0.00 a.u. and belongs to the point group C1. These results are very similar to my experimental results. Intuitively, it would be expected that the anti conformer would have the lowest energy since the torsion angle between terminal carbon groups is maximum, 180 degrees. The computational results show that the gauche 3 conformer is in fact the most stable conformers (-231.69266096 a.u.) According studies which implement Moller-Plesset perturbation theory and standard 6-31G* basis set (Gung et al), the gauche conformation also appeared to the lowest in energy. The main reason for this contradiction is thought to originate from the interaction of the pi electrons of the carbon carbon double bond and the nearby vinyl proton. This is referred to as the CH pi interaction.

Comparing the initially optimised Ci anti conformation of 1,5-hexadiene to the Appendix 1 results it is clear that both structures have the same point group Ci and both structures have similar energies (experimental: -231.69253506 and Appendix 1: -231.69254 a.u.) This supports the experimental optimisation calculation success.

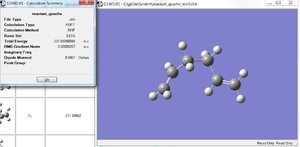
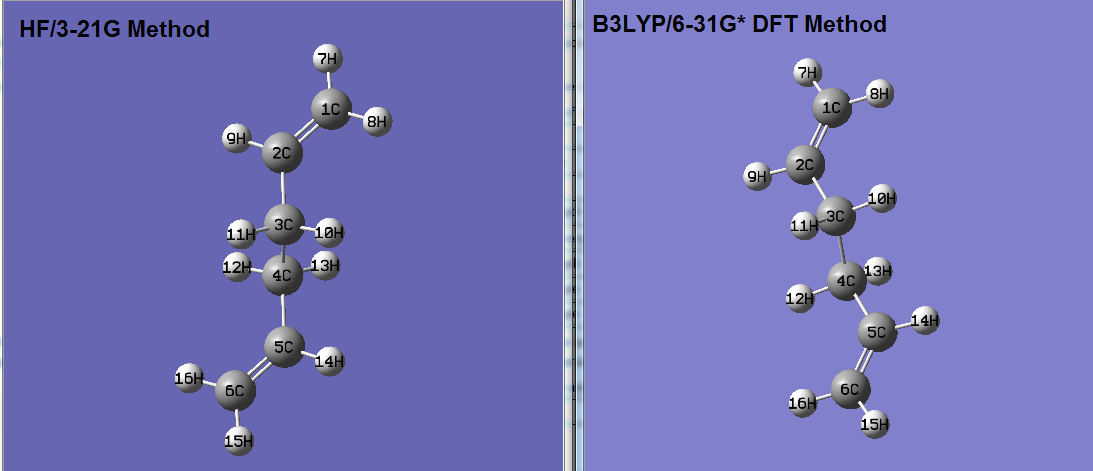
The Ci anti conformation of 1,5-hexadiene was re-optimised at the B3LYP/6-31G* level of theory which is slightly higher than the HF/3-21G method. The final results were compared, see table 2. A frequency calculation was also run on the anti confromation at both levels of theory, the absence of any negative frequencies shows that the structure was sucessfully optimised to a MINIMUM.

**Table 2: Comparison of optimised Anti 1,5-hexadiene at HF/3-21G amd DFT/B3LYP levels of theory**
Point of Comparison	HF/3-21G	DFT/ B3LYP
Point Group	Ci	Ci
Energy (a.u.)	-231.69253506	-234.61171553
C(1)=C2) Bond Length (BL)	1.31627	1.33350
C(2)-C(3) BL	1.50908	1.50404
C(3)-C(4) BL	1.55272	1.54818
C(4)-C(5) BL	1.50908	1.504040
C(5)=C(6) BL	1.31627	1.33350
C(5)=C(6) BL	1.31627	1.33350
(7)H-(1)C-(8)H Angle/ degrees	116.319	116.475
(7)H-(1)C-(2)C Angle/ degrees	121.862	121.864
(11)H-(3)C-(10)H Angle/ degrees	107.699	106.640

The overall structure of the anti conformation of 1,5-hexadiene is similar for both the DFT and HF theories. By comparing the final structures from both levels of theory it is clear the DFT method produces a reactant structure with a much lower energy. The C=C bond distances are slightly longer according to the DFT method, which suggests that the HF method over estimates the strength of the double bonds. Presence of longer bonds may also lead to slightly less steric clashes hence a lower energy. Both levels of theory show similar C-C single bonds lengths and the H-C-H and C-C-H angles are also similar.

**Table 3: Comparison of optimised frequencies of Anti 1,5-hexadiene at HF/3-21G amd DFT/B3LYP levels of theory**
Description	Frequency/cm-1	Intensity
DFT	940	71
DFT	3031	54
DFT	3137	56
DFT	3234	46
HF	1112	153
HF	3206	48
HF	3304	41
HF	3386	45

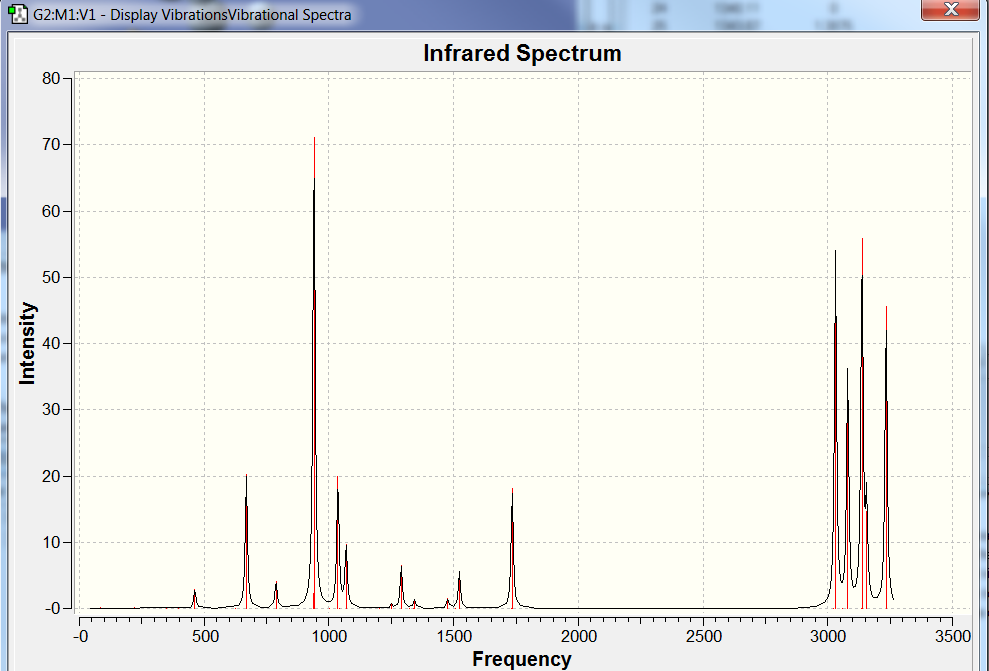
Table 3 shows some of the highest intensity vibrations of anit 1,5- hexadiene at both HF and DFT levels of theory. In general, all the frequency values were positive and none were negative. The presence of a negative frequency would indicate presence of a transition state. Some of the IR intensities were zero which means that at that particular frequency/energy there is no change in diploe moment hence the vibration is IR inactive .

Thermochemistry Information Note: all energy values are in a.u. units

Anti Peri Planar reactant: DFT/B3LYP

Thermal correction to Energy=                    0.149879
Thermal correction to Enthalpy=                  0.150823
Thermal correction to Gibbs Free Energy=         0.110969
Sum of electronic and zero-point Energies=           -234.469176
Sum of electronic and thermal Energies=              -234.461834
Sum of electronic and thermal Enthalpies=            -234.460890
Sum of electronic and thermal Free Energies=         -234.500743

Anti Peri Planar: HF/3-21G

Zero-point correction=                           0.152993 (Hartree/Particle)
Thermal correction to Energy=                    0.159964
Thermal correction to Enthalpy=                  0.160908
Thermal correction to Gibbs Free Energy=         0.121636
Sum of electronic and zero-point Energies=           -231.539542
Sum of electronic and thermal Energies=              -231.532571
Sum of electronic and thermal Enthalpies=            -231.531627
Sum of electronic and thermal Free Energies=         -231.570899

The Sum of electronic and zero-point Energies= Pottential energy at 0 K including the zero-point vibrational energy (E = Eelec + ZPE)

The Sum of electronic and thermal Energies= Energy at 298.15 K and 1 atm of pressure, includes contributions from the translational, rotational, and vibrational energy modes (E = E + Evib + Erot + Etrans).

The Sum of electronic and thermal Enthalpies contains an extra correction for RT (H = E + RT), particularly important when looking at dissociation reactions.

The Sum of electronic and thermal Free Energies = Entropic contribution to the free energy (G = H - TS)

Optimising the "Chair" and "Boat" Transition Structures

The aim running optimisation calculations is to locate a stationary point(s) of a given function. Stationary points have a first derivative value equal to zero. To determine whether the stationary point corresponds to a minimum or maximum the second derivative must be calculated, a positive second derivative result indicates a minimum stationary point and a negative result indicates a maximum point.

Multi dimensional functions often contain more than one stationary point hence there may be more than one local minima. This investigation focuses on modelling the potential energy surface of energy as a function of molecular geometry. Parameters such as molecular orbital’s and configuration state coefficients combined to give the energy of a wave function such as the Hartree Fock. The parameters are optimised using quadratic methods and linear equations are solved by matrix techniques to identify stationary points. Iterative methods are used to find the stationary points since most parameter that are used in the function are non-linear.

When calculating derivative values using computers it is important to realise that the answers generated are accurate to a specific degree of precision due to computational efficiency constraints. The degree of precision is dependant on the programme used. During this investigation the stationary points will be located as close as possible to the exact value and it is assumed that the optimisation calculation has successfully converged once a specific threshold level has been reached. The main disadvantage is that for systems with several flat potential energy surface regions the optimisation may appear to a artificially converged.

The steepest descent method was used to assess the molecular geometry at an energy minimum point. This simple (but computationally fast) method is based on evaluating the ‘sign’ of the gradient in a given direction i.e. negative or positive. The computer recognises negative gradients and when the function begins to ‘change direction’ and produce a positive gradient, a minimum point is registered in between the two points. One of the problems with this method is that as the minimum is approached the rate of convergence decreases hence the path with the steepest descent will never reach the minimum. Other methods for finding the optimum minimum points include: Conjugate Gradient methods and Newton-Raphson methods.

Optimising the Chair and Boat Transition Structures

To evaluate whether the transition state has been reached successfully it is necessary to consider the second derivative of the function. The Hessian is the second derivative matrix of a particular function. Calculating the Hessian is much more computationally demanding compared to gradient/optimisation calculations thus an updating scheme is often implemented as the optimisation occurs. This means that the gradients values at the previous and current points are used to generate a better Hessian approximation. The success of the transition state optimisation depends on the guess transition state structure.

The Cope rearrangement of 1,5- hexadiene can occur via "chair" or "boat" transition state (TS) structure. Each type of TS consists of two C3H5 allyl fragments positioned approximately 2.2 Å apart, one with C2h symmetry and the other with C2v symmetry.

In this experiment the single allyl fragment was optimized using the HF/3-21G level of theory. A ‘guess’ chair transition structure was created by creating a new MolGroup using two copies of the previously optimised allyl fragment. The distance between the terminal ends of the allyl fragments was set to 2.2 angstrom (termed the terminal distance for simplicity) using the GuassView ‘bond length’ feature. The closer the terminal distance is to real actual transition state equivalent the more reasonable the curvature of the surface is for points far away from the transition structure.

Several transition state (TS) optimisation methods were tested. It is difficult to locate the transition state since there is no defined correct method. There are two main types of TS calculations: local information based and interpolation between two minima.

Chair TS

TS( Berny ) Method 1

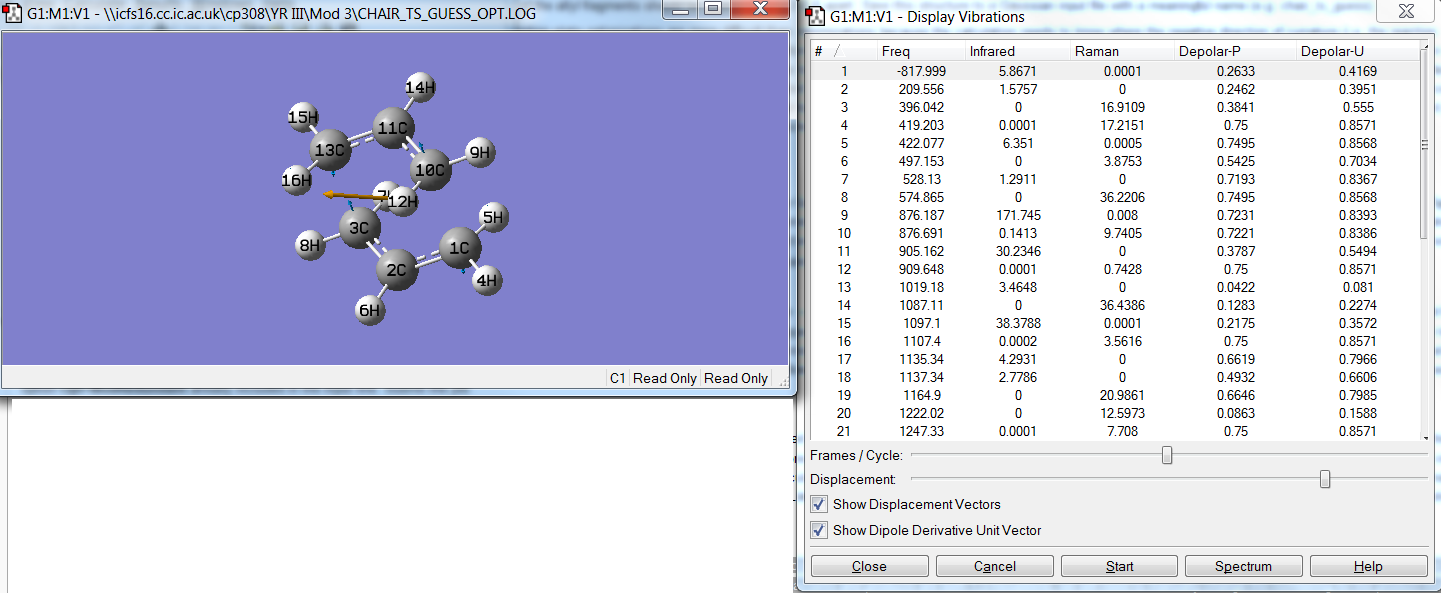
An optimisation and frequency calculation was run on the guess chair transition state using the following criteria: optimisationTS (Berny), Hartree Fock method, default basis set 3-21G. The force constants were chosen to be calculated once and the additional phrase: Opt=NoEigen’ was added to the keywords box to prevent the calculation crashing should more than one imaginary frequency appear. The job was submitted to Gaussian and successfully completed. The output file showed only one imaginary frequency at -817.99 cm-1 which is the frequency of the vibration that connects the reactant to products and thus leads to a decrease in the. This imaginery frequency is very similar to the expected single imaginary frequency 818 cm-1 . The animated vibration shows vibrations occuring around the bond forming region. There is also a stretching motion in the bond breaking region, which corresponds to the Cope rearrangement mechansim.

The energy of the HF/3-21G optimised chair transition state (point group C1) is -231.619224 a.u. , the RMS gradient norm was close to zero, 0.00001962 a.u. and the terminal C-C bond length was 2.02 Å. The success of Local method TS calculations depends on the quality of the TS guess structure.

Frozen Coordinate Method 2

The original guess chair transition state molecule was copied and pasted into a new MolGroup window so that the second optimisation method could be implemented. The frozen coordinate optimisation method was implement using the Redundant Coord Editor. The distance between opposite two terminal carbon atoms was frozen at 2.2 angstom and a HF/3-21G optimization was run. It is important that the initial frozen distance is reasonably close to the expected TS distance otherwise the calculation would fail. Once the calculation was complete, the two opposite terminal carbon distance were ‘un-frozen’ and the whole molecule was re-optimised using the redundant Coord Editor to select the Bond and Derivative options. A transition state optimisation was run without calculating the force constants and instead a normal guess Hessian would be modified and adopted to include information about the two coordinates differentiated along. The output file showed that the total Energy of the optimised chair transition state (point group C1) was E(RHF) -231.61932239 a.u. , the RMS gradient norm was 0.00002912 a.u. and the terminal bond C-C length was 2.02Å.

Both methods produce transition state structures with similar overall energies, the same point group and low RMS gradient norm values . For both methods the type of calculation performed was RHF and the same basis set was used since these parameters were kept consistent for both types of optimisations hence it is possible to compare energy values.

The TS (Berny) and Frozen Coordinate methods are examples of local methods of finding the saddle points (TS's) and require a good starting estimate of the the TS to converge. Since the molecule been studied is reasonable small Hessian based calculations of the second derivative are quite quick and inexpensive however deriving a second derivative matrix for larger moelcules would be much more computationally demanding.

Boat TS

The optimisation of the Boat TS was performed using the QST2 calculation. QST2 methods involve linear interpolation between the reactant and product structures to find out the otpimised saddle point. The disadvantages of this particular method is that for the interpolation to be sucessful, the geometry of the reactant and product material must be closely related to the expected geometry of the transition state geometry.

The numbering for the product molecule was mannually changed so that it corresponded to the numbering obtained if the reactant had rearranged. The initial optimisation failed as the reactant and product starting structures were too different form the TS structure.

To over come this problem, the reactant and product geometries were modified so that they were closer to the boat transition structure, both Reactant and product molecules were adjusted in the following way: the central C-C-C-C dihedral angle set to 0 degrees. Then the inside C-C-C angle was selectedd and reduce to 100 degrees.

After modification, the Boat TS structure was optimised according to the TS (QST2) option method and submitted to Guassian. The output file showed that that the total energy was -231.60280201 a.u. , the terminal C-C bond length was 2.14002 Å and only one invisable frequency was present , -839.45 cm-1 . The presence of just one negative frequency confirms the transition state structure, the motion of this vibration imitates asynchronous bond formation. The Boat TS optimisation was also run via the more reliable QST3 method and the results were very similar to that of the QST2 method. The QST3 output file showed that the total energy was -231.60280361 a.u., there was a single imaginery frequency at -839.85 cm-1 and the terminal C-C bond length was also 2.14 Å

Intrinisic Reaction Coordinate (IRC) Method

Optimisation methods are used to locate the saddle points on an energy surface. Once the TS location has been identified a calculation can be performed to ascertain the minima starting material via the steepest descent path. At the saddle point, the vibrational normal coordinate corresponding to the imaginery frequency is the reaction coordinate. To confirm that this specific imaginery frequency corresponds of the correct TS one can calculate the Minimum Energy Path.

When the Minimum Energy Path is located in mass-weighted coordinates it is called the Intrinsic Reaction Coordinate (IRC). The IRC assumes that the reaction occurs in the limit of a zero temperature. The IRC calculation was performed on the HF/3-21G optimised Chair TS, the force constants were only computed once at the start of the calculation and teh

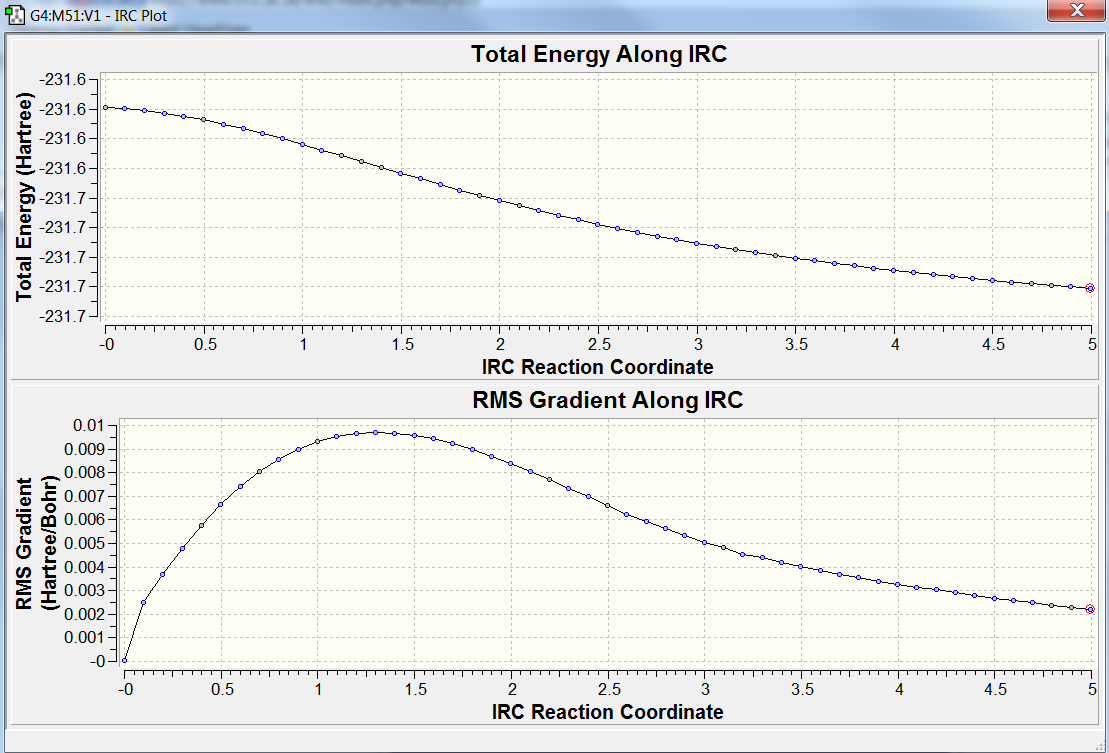
This creates a series of points by taking small geometry steps in the direction where the gradient or slope of the energy surface is steepest and tells us which conformers of 1,5-hexadiene the transition structures connect. This calculation was run on the HF / 3-21G optimised chair TS. The computation of the force constants was set as once and 50 steps along the IRC path. The calculation was run and the results showed that the mimium conformer of 1,5-hexadiene had not been reached. The total energy was -231.68866694 a.u. , the RMS gradient norm was -0.0024926 a.u and the point group after symmetrisation was C2, see graph below for stepwise energy changes.

Several other IRC calculations were performed in attempt to located a more accurate mimima conformation.

Trial 1: An IRC calculation was performed by taking the last point on the IRC, running a normal minimization. The results showed that the total energy of the conformer was lower that the inital method, -231.69166702 a.u. , the RMS gradient was 0.00000263 a.u. and the point group was also C2. This conformer has a similar energy to the 'wiki' gauche2 conformer -231.69167 a.u. total energy.

Trial 2: An IRC calculation was performed and the force constants were calculated at every step (N=100)- which enables the computer to assess as each step whether the gradient is negative i.e. moving down the minimum energy pathway of the potential energy surface and when the force constant becomes positive the programme will stop the itterative calculation. The results showed that the total energy was -231.69166433 a.u. and the gradient norm was 0.00001135 a.u.

Both trials 1 and 2 produces structures with similar energies, trial 1 energy was slightly lower, which is reflective of the gauche 2 conformer.

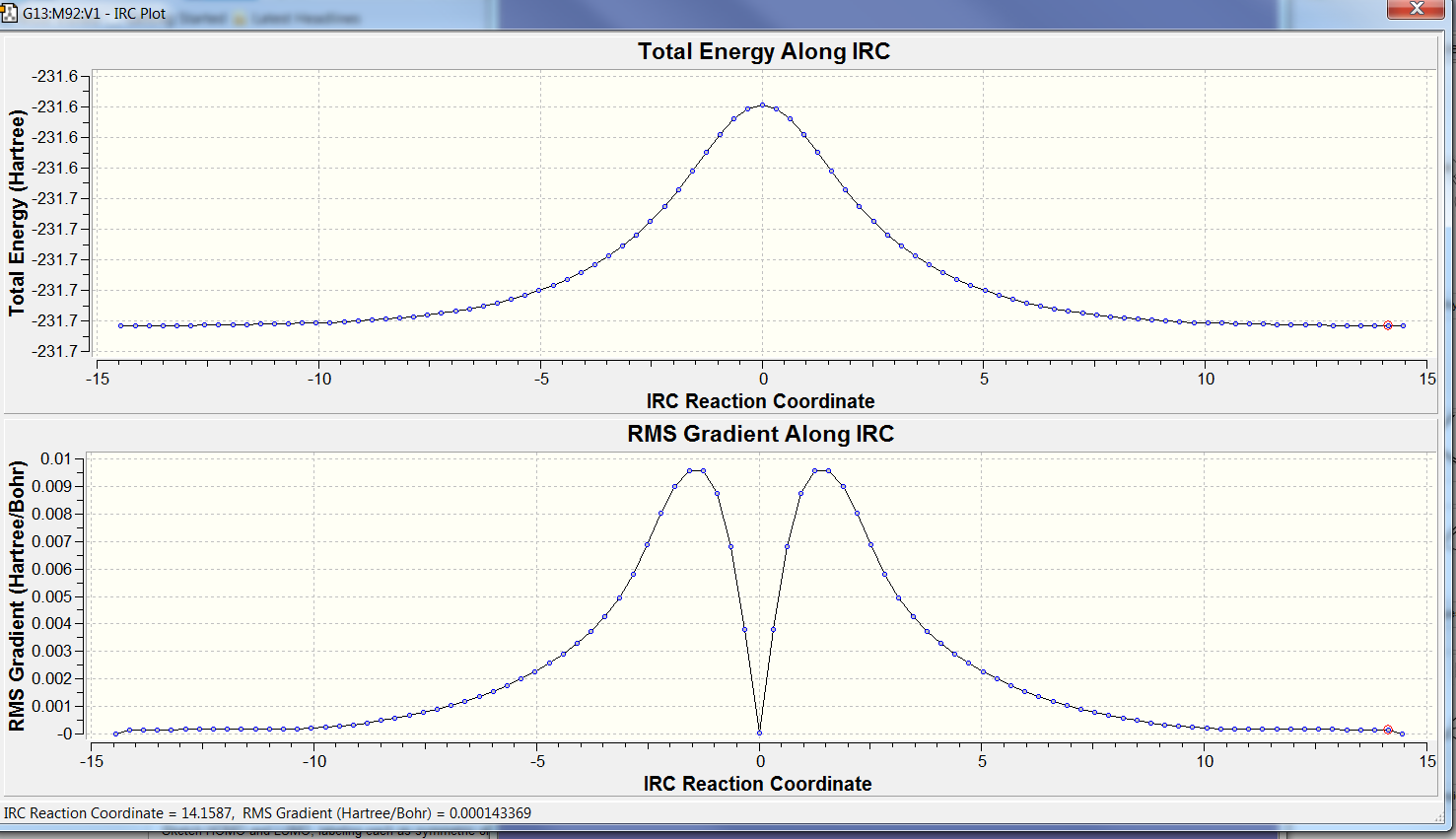
To confirm that the reaction coordinate is symmetrical, the IRC calculaiton was run in both directions for trial 2. The graph below illustrates the symmetrical nature of the the reaction, as the the Total Energy and RMS gradient along the IRC graphs both have a plane of symmetry.

Activation Energies For The Transition Structures

Summary of energies (in hartree)

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.61932101	-231.46670514	-231.461391	-234.55698181	-234.414918	-234.409012
Boat TS	-231.60280246	-231.450929	-231.445311	-234.54309302	-234.402340	-234.396004
*Reactant (anti2)*	-231.692535	-231.539542	-231.532571	-234.61171553	-231.539542	-231.532571

*1 hartree = 627.509 kcal/mol

Summary of activation energies (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.70	45.94	34.06	34.34	33.5 ± 0.5
ΔE (Boat)	55.60	56.31	41.96	43.06	44.7 ± 2.0

Thermodynamic data can be used to asses the activation energies for the reaction path. The HF and DFT theories both show that the chair TS conformation is has a relatively lower energy than the boat TS thus it is possible to state that the chair conformation is more stable. The reactant (anti 2 conformer) - TS activation energy is lower for the chair conformer according to both theory levels.

The Diels-Alder Cycloaddition

The Diels Alder reaction belongs to the class a Pericyclic reactions, specifically a [4π+2π] Cycloaddition. During this reaction two new σ bonds are formed between an electron deficient dienophile and an electron rich diene molecule beacuse of favourable π-orbital interactions between the HOMO/LUMO of the dienophile and diene which result in the end product. There are no intermediates involved in Pericylic reactions, the reaction is concerted and instead goes via a aromatic 6 π electron transition state. Whether or not the reactions occur in a concerted stereospecific fashion (allowed) or not (forbidden) depends on the number of π electrons involved.

For this section of the investigation all optimisations have been calculated using the Semi-Empirical/AM1 method followed by a more accurate DFT/B3LYP/6-31G* level of theory.

Cis-Butadiene and Ethylene

The table below shows the HOMO/LUMO's for cis-butadiene and ethylene. Both Reactants HOMO/ LUMO have opposite symmetry hence for a reaction to occur the HOMO of one react must interact with the LUMO of the other reactant.

Transition State

For this part of the investigation the frozen coordinate method was used. First both reactants were individually optimised at the Semi-Empirical Level AM1. The fragments were then placed in a single window and the C-C bond distance was set at 2.2Å. The structure was optimised to a TS( Berny ) level and the resultant structure was re-optimised with the C-C coordinates unfrozen. The final structure was then optimised at a more accurate level DFT/ B3LYP / 6-31G (d).

The output file results for the following methods of optimisation were as follows:

Semi-empirical/AM1:

-Energy/ a.u. :  0.11165631 
-C-C Bond Forming Distance: 2.08 Å
-Imaginary Frequency / cm-1 : -956.86

DFT/B3LYP/6-31G(d):

-Energy/ a.u. : -234.54389654 
-C-C Bond Formign Distance: 2.25 Å 
-Imaginary Frequency/ cm-1 : -524.82

It is important to realise that since two different types of theory have been used to AM1 and DFT it is not possible to make any energy related comparisons. Both AM1/DFT methods show the presence of one imaginary frequency, confirming a transition state. The actual values of the imaginary frequencies are quite different due to the different levels of accuracy however the motion of both vibrations is very similar.

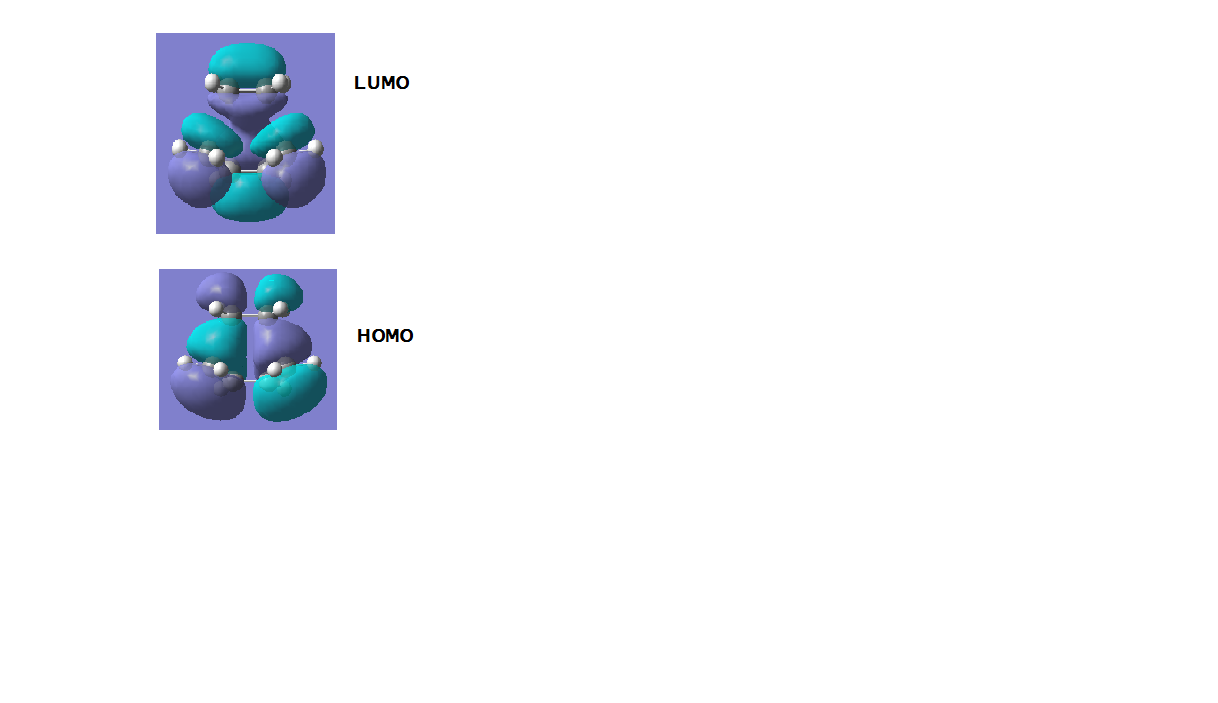
The image below shows the results of the MO diagrams for the reaction transition state:

-LUMO Energy : 0.023 a.u. SYMMETRIC symmetry MO
-HOMO Energy: -0.323 a.u. ANTI-SYMMETRIC symmetry MO

The LUMO TS diagram shows that the main contributions originate from the HOMO of the ethylene molecule and the LUMO of the s-Cis butadiene moelcule which leads to out of phase anti bonding overlap. Conversely, the HOMO TS diagram shows that the main contributions originate from the LUMO of the ethylene and the HOMO of the s-Cis butadiene moelcule which leads to in phase sigma bonding overlap. Since the HOMO of butadiene and the LUMO of ethylene are both antisymmetric about the reflection plane hence the reaction is allowed and obeys the conservation of orbital symmetry theory.

-The average C-C bond length (with both carbons containing sp3 hybridisation) is 1.54Å.

-The average C=C double bond length (with both carbons containing sp2 hybridisation) is 1.33Å.

According to the computational TS optimised results at the DFT level of theory the C-C single bond length is 1.39Å and the C=C double bond length is 1.40Å . This shows that at the TS the C=C double bonds are longer than usual hence they are breaking, to form a single C-C bond. The Van der Waals atomic radius for Carbon atoms is approximately 1.70Å. The bond forming length is 2.25 Å which is less than two times the Van der Waals radius multiplied which is representative of an incomplete reaction- the carbon atoms are not close enough to form a bond.

Literature Reference

Elements of Organic Chemistry I, Professor C.Wamser, 199

Element Radius List : www.ccdc.cam.ac.uk/products/csd/radii/table.php4

Endo and Exo Transition States

**Table: Exo vs Endo TS comparison**
Feature	Endo TS	Exo TS
Motion		Motion File:Exomotion.gif
Energy HOMO (a.u.)	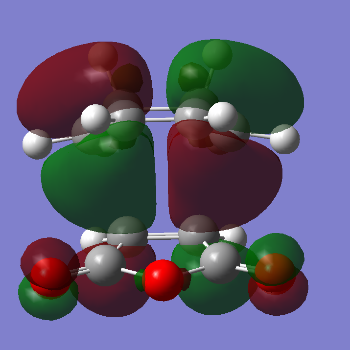Energy: -0.241, Anti-Symmetric	Energy: -0.242, Anti-Symmetric
Energy LUMO (a.u.)	Energy : -0.067, Anti-Symmetric	Energy: -0.078, Anti-Symmetric
Imaginary Frequency at DFT B3LYP/6-31G(d) Theory / cm-1	-447	-448
Total Energy/ a.u.	-612.68339604	-612.67931087

The table above shows the motions, energies HOMO/LUMO, imaginary frequencies and total energies of the Endo and Exo TS's. The length of the C-C forming bond in the the endo and exo TS were similar 2.27 and 2.28 angstroms respectively.

Both Endo and Exo TS's contain one imaginary frequency which illustrates the presence of a transition state. The vibrational motions exerted by both TS is reflective of the formation of the two C-~C bonds during the concerted cycloaddition reaction.

Intuitavely, one would expect the Exo TS to be more stable than the Endo due to steric hindrance reasons leading to unfavourably higher energies. However the results show that the total energy of the Endo product is slightly lower than the Exo product.The reason for this unexpected major product result can be explained by Frontier Molecular Orbital theory.

Maleic anhydride exerts an electron withdrawing effect hence the alkene C=C bond is electron deficient. The Diel's Alder reaction occurs between the HOMO of the 1,3 cyclohexadiene and the LUMO of of the maleic anhydride (consists of a pi* C=C antibonding orbital). When the HOMO of the diene interacts with the antibonding C=C LUMO of the dienophile the C=C dienophile double bond breaks and forms a single C-C bond.

It is important to realise that the terms Endo and Exo refer to the orientation of substituentsin the transition state. The Endo TS is lower due to the in phase stabilising secondary (non-bonding) orbital interactions between the Carbon bonds involved in the pi system of the 1,3 cyclohexadiene, which approaches maleic anhydride from above, and the pi* C=O antibonding orbitals in the maleic anhydride molecule. Overall, this makes the endo transition structure more stable. The Exo TS does not experience any favourable secondary orbital interactions since the C=O groups in maleic anhydride face away from the diene pi system in 13, cyclodexadiene.

1,3-cyclodexadiene and maleic anhydride were also optimised at DFT level of theory so that the activation energy of both Endo and Exo TS's could be calculated. By combining the two reactants energies together and subtracting this value from the TS energies of both TS's, the activation energies could be calculated. The activation energy of the Endo TS was approximately 0.04 a.u. lower than the exo TS which supports the idea of stabilising secondary overlap interactions in the Endo case.