3rd Year Computational Lab Physical Module: Transition states and reactivity

The software Gaussian 09w was used to perform all calculations in this computational experiment.

The Cope Rearrangement of 1,5-hexadiene

The cope rearrangement of 1,5-hexadiene [3,3]-sigmatropic rearrangement reaction.For a long time its machanism was controversial.There have been many experimental and computational studies and nowadays it is generally believed that it is a conserted reaction in which all bond breaking and bond making occurs in a single step, via either a "boat" or a "chair" transition state.^[1]The "chair" transition state is considered to be lower in energy and this was proved in the computational experiment.The activation energy (temperature=0K) of the "chair" geometry (34.07 kcal/mol) is lower than that of the "boat" geometry (41.98 kcal/mol) at the B3LYP/6-31G* level of theory.

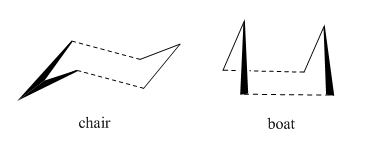
**Figure 1.** *Chair and boat conformations*

1,5-hexadiene

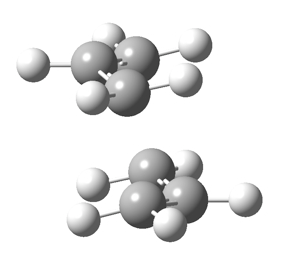
Firstly, the structure of 1,5-hexadiene with an "anti" linkage for the central four C atoms was optimised at the HF/3-21G level of theory.

The results of frequency calculation at the HF/3-21G level of theory were summarized in Table 1:


Type of Energies	Description	Energy/Ha (HF/3-21G)
Sum of electronic and zero-point energies	E = E_elec+ZPE	-231.5395
Sum of electronic and thermal energies	TE = E + E_vib + E_rot + E_trans	-231.5326
Sum of electronic and thermal enthalpies	H = E +RT	-231.5316
Sum of electronic and thermal free energies	G = H - TS	-231.5709

Table 1. Frequency calculations of 1,5-hexadiene (anti2) optimized at HF/3-21G

The electronic energy was calculated to be -231.6925 Ha with Ci symmetry point group. This structure is equivalent to anti2 (Figure 2) according to the table in Appendix 1.

1,5-hexadiene (Anti)

Figure 2. 1,5-hexadiene (anti2)

After that, the structure of 1,5-hexadiene with a "gauche" linkage for the central four C atoms was optimised again at the HF/3-21G level of theory.The electronic energy after optimization was calculated to be -231.6927Ha with C1 symmetry. This structure is equivalent to the gauche3 structure (Figure 3) according to the table in Appendix 1.

1,5-hexadiene (Anti)

Figure 3. 1,5-hexadiene (Gauche3)

The optimized anti2 structure was then re-optimized at the B3LYP/6-31G* level and the electronic energy was calculated to be -234.6117 Ha. The strucure was lower in energy after re-optimization with the symmetry point group Ci. The overall geometry change was very small. B3LYP/6-31G* level is an improvement^[2] over the HF/3-21G level because the polarisation of atoms is considered hence more accurate orbitals can be calculated.

A frequency calculation was run at the same level of theory using the re-optimized structure and the results was shown in Table 3.


Type of Energies	Energy/Ha *(B3LYP/6-31G)**
Sum of electronic and zero-point energies	-234.4692
Sum of electronic and thermal energies	-234.4619
Sum of electronic and thermal enthalpies	-234.4609
Sum of electronic and thermal free energies	-234.5008

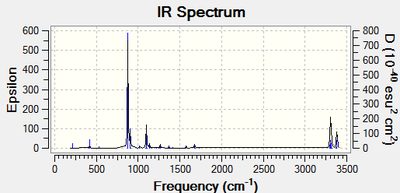
Table 3. Frequency calculations of 1,5-hexadiene (anti2) optimized at B3LYP/6-31G*

The IR spectrum has been visualised as in Figure 4.No imaginary (negative) frequenciy was observed.

The "Chair" and "Boat" Transition States

"Chair" transition strucure

Puzzle globe — **Figure 5.** *Allyl Fragment*

Firstly an allyl fragment (C₃H₅,Figure 5) was optimized at the HF/3-21G level of theory.The structure after optimisation was similar to half of the "chair" transition state. Therfore two of the fragments was placed together with rotation with a distance of ~2.2 Å between the terminal ends. After that,two different methods were used to optimise the transition state.

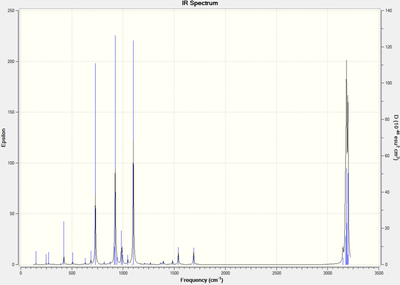
The first approach was to optimise the chair transition state to a TS (Berny) at the HF/3-21G level of theory (Figure 6).The force constant was calculated once and "Opt=NoEigen" was typed in the additional keyword box to stop the calculation crashing if more than one imaginary frequency was detected. The electronic energy was calculated to be -231.6193Ha with C₂h symmetry.The distance between the terminal ends of the allyl fragments were 2.0207Å (Figure 8) and the frequency calculation were performed simultaneously giving an imaginary frequency of -818 cm^-1 corresponding to the Cop rearrangement transformation via the "chair" transition state. The sum of energies were calculated as in Table 4. The generated IR spectrum was shown in Figure 7.


Type of Energies	Energy/Ha (HF/3-21G)
Sum of electronic and zero-point energies	-231.4667
Sum of electronic and thermal energies	-231.4613
Sum of electronic and thermal enthalpies	-231.4604
Sum of electronic and thermal free energies	-231.4952

Table 4. Frequency calculations of the chair transition state optimized at HF/3-21G

An animation of this transition state vibrations was simulated in Figure 8.

The second "frozen coordinate method" fixed the distance between the terminal ends to 2.2 Å, then the transition state was optimised.The electronic energy was calculated to be -231.6148 Ha. The resulting geometry looked very similar as the previous method except that the distance between the terminal ends were fixed to 2.2 Å. After that each of the bonds that was frozen was optimised without calculating the force constant. The resulting electronic energy were -231.6193 Ha and the distance between the terminal ends of the allyl fragments were 2.0206Å.

The two different methods have calculated out the same electronic energy and very similar distances between the terminal ends with negligible diffrrence (0.0001Å). Therefore from the ageement between the two methods it can be concluded that both methods has achieved a satisfying result.

"Boat" transition strucure

To optimise the structure of "boat" transition state, a different method called "QST2 method" was used in which the reactants and products for the reaction were specified and then the transition state was calculated between the two structures. Firstly the reactant and the product (both 1,5-hexadiene) were numbered in the same way manually as shown in Figure 9.

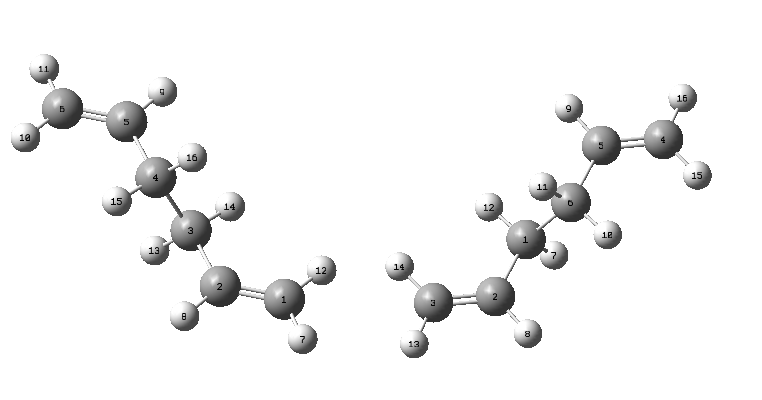
The molecules were optimised at HF/3-21G using the QST2 calculation. However the job failed to approach the "boat" structure and it resulted in a structure that looked like the "chair" structure (Figure 10) with C_2h symmetry.

In order to achieve the desired structure, modifications have been made on the geometries of both the reactant and the product. The central C-C-C-C dihedral angles was adjusted to 0° and the inside C-C-C angles were reduced to 100°as shown in Figure 11.

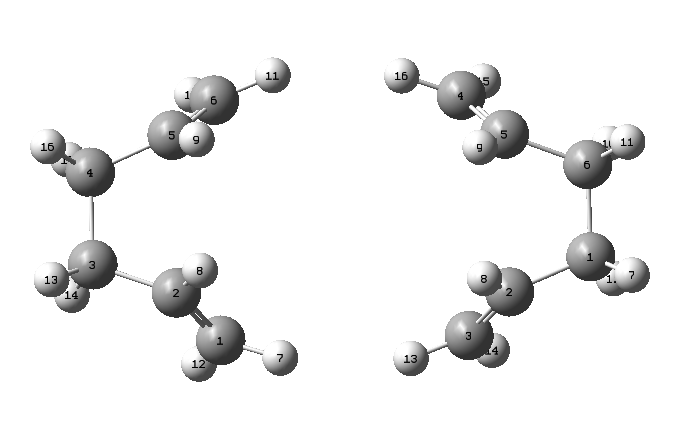
The second attempt after the modification of starting molecules successflly achieved the desired "boat" transition state with C_2v symmetry.(Figure 12).

The electronic energy was -231.6028 Ha. The distance between the terminal ends of the allyl fragments was calculated to be 2.1400Å. The sum of energies were calculated as shown in Table 7.


Type of Energies	Energy/Ha (HF/3-21G)
Sum of electronic and zero-point energies	-231.4510
Sum of electronic and thermal energies	-231.4453
Sum of electronic and thermal enthalpies	-231.4444
Sum of electronic and thermal free energies	-231.4798

Table 7. Sum of energies of the "boat" transition state optimized at HF/3-21G

An animation of this transition state vibrations was produced in Figure 13.

The calculation gave an imaginary frequency of magnitude 840 cm-1 corresponding to the Cop rearrangement transformation via the "boat" transition state. Furthermore,the reactant, product and proposed "boat" transition state were optimised using QST3 calculation. The resulting "boat" transition structure has the same electronic energy as the previous method (-231.6028 Ha), but a slightly smaller distance (2.1384Å) between the terminal ends of the allyl fragments.

Another QST2optimization attempt has been done at B3LYP/6-31G* level of theory. The electronic energy was found to be -234.5431Ha with C_2v symmetry point group. The energies results were summarized in Table 8.


Type of Energies	Energy/Ha *(B3LYP/6-32G)**
Sum of electronic and zero-point energies	-234.4023
Sum of electronic and thermal energies	-234.3960
Sum of electronic and thermal enthalpies	-234.3951
Sum of electronic and thermal free energies	-234.4318

Table 8. Sum of energies of the boat transition state optimized at B3LYP/6-31G*

The activation energies of the boat transition state were calculated by using the data in Table 7. and Table 8. .


	Energy (kcal/mol)
0K (HF/3-21G)	55.60
298.15K (HF/3-21G)	54.78
0K (B3LYP/6-31G*)	41.98
298.15K (B3LYP/6-31G*)	41.35

Table 9. Activation energies of the boat transition state optimized at HF/3-21G and B3LYP/6-31G*

The Diels Alder Cycloaddition

Cis-butadiene

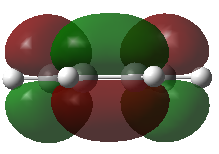
The structure of cis-butadiene has been optimized using the AM1 method and the HOMO and LOMO of this molecule were visualized. The HOMO of of this moleculs is anti-symmetric (Figure 19) while the LUMO is symmetric (Figure 20) with respect to plane.

**Figure 11.** *HOMO of transition state of reaction between cis-butadiene and ethylene*

**Figure 12.** *LUMO of transition state of reaction between cis-butadiene and ethylene*

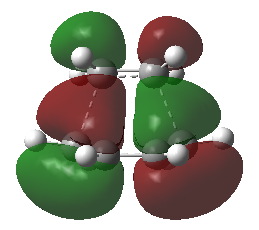
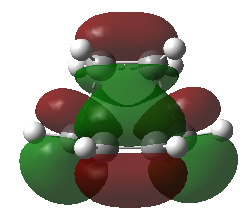
Transition state of the reaction between ethylene and butadiene

The transition state of the reaction was determined using QST2 method. The atoms of the reactants and products were renumbered beforehand as shown in Figure 9.

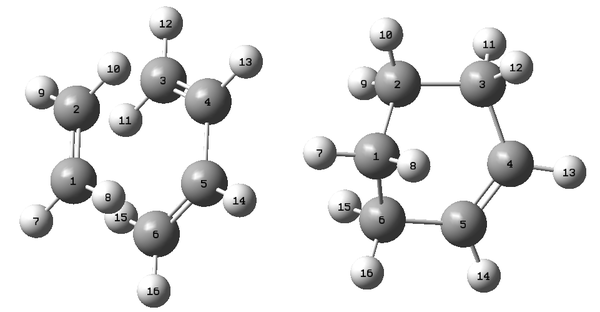
**Figure 9.** *The atoms of the reactants (left) and the product (right) were renumbered before optimisation*

Tthe bond lengths of two partly formed C-C bonds were measured to be 2.12Å. The typical sp3 and sp2 C-C bond lengths are 1.54 Å and 1.47 Å respectively. The van der Waals radius of the C atom is 1.7 Å^[3].^[4] The calculated bond distance of the transition structure is greater than typical bond lengths but it is still within the van der Waals radius.

The vibrational frequencies were also calculated and an infrared spectrum was produced (Figure 10). An imaginary frequency of magnitude -955 cm-1 was seen.And the vibration at 147 cm-1 is the lowest positive frequency which does not correspond to the bonds forming transformation but the reactants vibrating.

**Figure 10.** *Generated IR of transition state of reaction between cis-butadiene and ethylene*

The HOMO and LUMO molecular orbitals of this transition structure were visualized in Figure 11 and Figure 12 respectively.The HOMO of the transition structure is anti-symmetric while the LUMO is symmetric. Thus this transition state HOMO is formed by the HOMO of cis-butadiene and the LUMO of ethylene because they are all anti-symmetrical.

References

↑ Cope, A. C.; Hardy E. M. J. Am. Chem. Soc. 1940, 62, 441.
↑ Nigerian Journal of Chemical Research, 2007, 12. DOI:10.4314/njcr.v12i1.
↑ Z. Naturforsch., 2007, 62b, pp 235-243.
↑ Rowland RS, Taylor R (1996). "Intermolecular nonbonded contact distances in organic crystal structures: comparison with distances expected from van der Waals radii". J. Phys. Chem. 100 (18): 7384–7391,

[1] Cope, A. C.; Hardy E. M. J. Am. Chem. Soc. 1940, 62, 441.

[soo-2] Nigerian Journal of Chemical Research, 2007, 12. DOI:10.4314/njcr.v12i1.

[bondlength2-3] Z. Naturforsch., 2007, 62b, pp 235-243.

[4] Rowland RS, Taylor R (1996). "Intermolecular nonbonded contact distances in organic crystal structures: comparison with distances expected from van der Waals radii". J. Phys. Chem. 100 (18): 7384–7391,

[1]

[2]

[3]

[4]