Rep:Mod:wsc108 module1

Aims and Objectives

The aim of this module was to investigate the use of molecular mechanics, semi-empirical molecular orbital and DFT-based molecular orbital methods for structural and spectroscopic evaluations. Molecular mechanics methods were employed to predict the geometry and regioselectivity of the hydrogenation of cyclopentadiene dimer and the conformation of an intermediate in Taxol. Semi-empirical molecular orbital methods were used to determine the stereochemistry of nucleophilic addition to two different pyridinium analogues and the regioselectivity of the electrophilic carbenylation of a chloro-substituted bicyclic diene. Finally, DFT-based molecular orbital methods were used to study the neighbouring group participation of C-Cl and C=C stretching frequency of the chloro-substitued bicyclic diene. A mini-project involving a domino Michael-Henry reaction was also completed using DFT molecular orbital theory to investigate ¹³NMR and infrared spectroscopy as well as optical rotation simulations.

Cyclopentadiene

Dimerisation of Cyclopentadiene

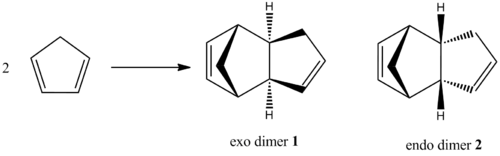
Cyclopentadiene dimerises via a Diels Alder mechanism to form 2 possible isomers - the exo dimer 1 and endo dimer 2. However, based on literature, the endo dimer 2 is formed exclusively although some exo dimer 1 was formed on heating. To explain this observation, the MM2 method is used to perform geometry optimisation on the two dimers in ChemBio3D-12.0 and the relative energies of dimers 1 and 2 are compared.

Figure 1: Dimerisation of Cyclopentadiene

The optimised geometry of both exo dimer 1 and endo dimer 2 can be seen here:

Table 1: Relative Energies of Exo-Dimer 1 and Endo-Dimer 2

	Energies/ kcal mol-1						Energies/ kJ mol-1
	Stretch	Bend	Torsion	Van der Waals	Dipole-Dipole	Total	Stretch	Bend	Torsion	Van der Waals	Dipole-Dipole	Total
Exo-Dimer 1	1.29	20.57	7.66	4.23	0.38	31.88	5.40	86.06	32.05	17.70	1.59	133.40
Endo-Dimer 2	1.25	20.88	9.50	4.30	0.45	34.00	5.23	87.36	39.75	17.99	1.88	142.26

The exo-dimer 1 is 8.86 kJ mol^-1 lower in energy than the endo-dimer 2. This implies that the exo-dimer 1 is the thermodynamically favourable product of dimerisation whereas the endo-dimer 2 is the kinetically favourable product. Since it is observed experimentally that the endo-dimer 2 is the major product formed, it can be seen that the kinetically favourable product is favoured. Hence, based on the results obtained from the molecular mechanics technique, it can be seen that cyclodimerisation of cyclopentadiene is kinetically controlled. It is a common misconception that Diels-Alder reactions are readily reversible, hence kinetic products are produced under mild conditions whereas thermodynamic products are produced under more forcing conditions which allow equilibration to take place. However, the vast majority of Diels-Alder reactions are irreversible, hence the kinetically favoured product is often the major product. Thus, in the dimerisation of cyclopentadiene, the kinetically favoured endo-dimer 2 is the major product observed instead of the thermodynamically favoured exo-dimer 1. As the Diels-Alder reaction here is a concerted process, the exclusive stereoselection can be rationalised by the Woodward-Hoffmann rules, where orbitals of both molecules interact in a suprafacial manner, resulting in an exclusive syn addition. It was found that such a preferential way of attack favours the formation of the endo product.

Hydrogenation of Cyclopentadiene Dimer

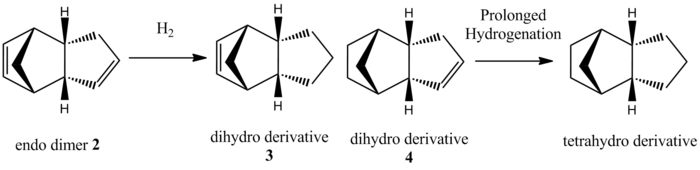
Based on literature, hydrogenation of the endo-dimer 2 forms the dihydro product 4. The tetrahydro derivative is only formed after prolonged hydrogenation. Again, to explain this observation, the MM2 method is used to perform geometry optimisation on ChemBio3D-12.0 and the relative energies of dihydro products 3 and 4 are compared.

Figure 2: Hydrogenation of Cyclopentadiene Dimer

The optimised geometry of dihydro products 3 and 4 can be seen here:

Table 2: Relative Energies of Dihydro Derivatives 3 and 4

	Energies/ kcal mol-1						Energies/ kJ mol-1
	Stretch	Bend	Torsion	Van der Waals	Dipole-Dipole	Total	Stretch	Bend	Torsion	Van der Waals	Dipole-Dipole	Total
Dihydro Product 3	1.23	18.92	12.17	5.73	0.16	35.93	5.16	79.16	50.92	23.98	0.68	150.32
Dihydro Product 4	1.11	14.53	12.51	4.50	0.14	31.16	4.63	60.78	52.33	18.84	0.59	130.39

The dihydro product 4 is 19.93 kJ mol^-1 lower in energy than the dihydro product 3. This suggests that the dihydro product 4, which is the major product observed experimentally, is the thermodynamically stable product. Hence, based on the results obtained from the molecular mechanics technique, it can be seen that hydrogenation of cyclopentadiene dimer is thermodynamically controlled. It is observed that the bending energy contributes largely to the difference in total energy of products 3 and 4, while the stretch, torsion, Van der Waals and dipole dipole energies are fairly similar. The stability of the products could be rationalised by considering the C-C=C angle in both products. The C-C=C angle is ~108^o and ~113^o in dihydro product 3 and 4 respectively. As the C-C=C angle in product 4 is closer to the ideal sp² angle of 120^o, there is less ring strain present in product 4, hence rendering it much more stable than product 3.

Stereochemistry of Nucleophilic Additions to a Pyridinium Ring (NAD+ analogue)

Reaction of N-Methyl Pyridoxazepinone with Grignard Reagent

The optically active N-methyl pyridoxazepinone 5 reacts with Grignard reagent, MeMgI, via nucleophilic addition to form product 6. As can be seen below, alkylation of the pyridine ring at the 4-position is stereospecific. Based on literature, the electropositive Mg coordinates to the electronegative carbonyl oxygen, resulting in the attack of the Me^- nucleophile on the 4-position of the pyridine ring. Hence, this implies that the geometry of the carbonyl group with respect to the pyridine ring would determine the stereochemistry of the final product.

Figure 3:Reaction Mechanism of 5 to 6

As ChemBio3D 12.0 has introduced a bug which affects the molecular mechanics force field when applied to molecules with N⁺ atom, a non-mechanics method PM6 was used to perform the geometry optimisation here. By fixing the dihedral angle between C=O and the pyridine ring to negative and positive values, the energy of the optimised molecule was noted and compared to the structure in which the dihedral angle is 0^o. The reactant MeMgI could not be included in the structure in ChemBio3D as the element Magnesium is not recognised by the programme.

It was noted that for negative dihedral angles where C=O lies below the ring, and the molecule does not reach a low energy conformation. However, for positive dihedral angles, a minimum energy conformation is observed when the dihedral angle is 28^o above the plane of the ring. As the most stable conformation has the C=O being above the plane of the ring, the electropositive Mg of the Grignard reagent would coordinate to C=O above the plane of the ring. This results in the attack of the nucleophile Me^- from the top of the ring, hence explaining the stereochemistry observed in 6.

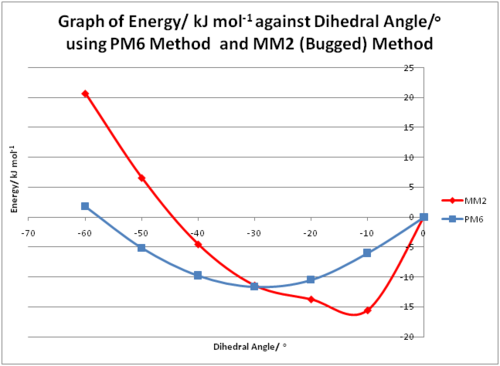
Some of the results of the positive dihedral angles are shown in the table and graph below. It is important to note that the energy given is relative to the structure in which the dihedral angle is 0^o. As can be seen from the two graphs below, the MM2 and PM6 methods give different trends and different dihedral angles for the most stable conformation. This shows that the MM2 method is indeed bugged.

Table 3: Relative Energies of Different Conformations with Different Dihedral Angles

Dihedral Angle/o	MM2/ kJ mol-1	PM6/ kJ mol-1
0	0.00	0.00
5	-9.44	-0.97
10	-10.10	-2.22
15	-9.52	-2.98
20	-7.73	-3.09
22	-6.78	-3.02
24	-5.45	-2.79
26	-3.94	-2.42
28	-2.54	-3.57
30	4.22	-3.02
35	9.12	-1.21
40	15.39	1.20

Figure 4:Graphs of Energy against Dihedral Angles using MM2 and PM6 Methods

It is interesting to note that an increase in 2^o in the dihedral angle from 26^o to 28^o resulted in a stabilisation of ~1kJ/mol^-1. One possible reason for this could be due to the nature of the PM6 method employed in the calculation. One of the objectives of PM6 is to improve the modelling of hydrogen bonds, hence PM6 makes use of an equation with an exponential term that would be significantly reduced at hydrogen bonding distances, resulting in an increased in hydrogen bond interaction energy. The hydrogen bond between O and the nearest H is 2.23Å and 2.25Å when the dihedral angle is 26^o and 28^o respectively. Hence, the optimal hydrogen bonding distance between O and H in this molecule could possibly be 2.25Å, hence resulting in a much stable conformation formed at that distance.

The optimised structure of Compound 5 when the dihedral angles are 26^o and 28^o can be viewed here:

Reaction of N-Methyl Quinolinium Salt with Aniline

Figure 5: Reaction Mechanism of 7 to 8

Similarly, the N-methyl quinolinium salt 7 reacts with aniline via a nucleophilic addition reaction. However, unlike the reaction between N-methyl pyridoxazepinone with the Grignard reagent where electropositive Mg⁺ is attracted to the electronegative carbonyl oxygen, there is no coordination of NH₂(Ph) to the carbonyl. In fact, as NH₂(Ph) is electron rich, there would probably be a slight repulsion between it and the electronegative carbonyl oxygen. Hence, to explain the stereochemistry observed in 8, the dihedral angle between C=O and the ring is fixed to negative and positive values and the energy of the optimised molecule was noted and compared to that when the dihedral angle is at 0^o as well.

It was noted that no low energy conformation was found for positive dihedral angles, where C=O lies above the ring. Again, a significantly different trend is observed when PM6 and MM2 are used. Based on the MM2 and PM6 methods, the most stable conformation are when the dihedral angles are approximately -30^o and -10^o respectively. This difference again confirms that the MM2 method is bugged. Some of the results of the dihedral angles are shown in the table and graph below. Again, the energy given is relative to the structure in which the dihedral angle=0^o.

Table 4: Relative Energies of Different Conformations with Different Dihedral Angles

Dihedral Angle/o	MM2/ kJ mol-1	PM6/ kJ mol-1
-60	20.67	1.79
-50	6.55	-5.11
-40	-4.57	-9.74
-30	-11.44	-11.62
-20	-13.77	-10.47
-10	-15.61	-5.99
0	0.00	0.00

Figure 6: Graphs of Energy against Dihedral Angles using MM2 and PM6 Methods

As can be seen from Figure 6 above, based on the PM6 method, the most stable conformation obtained is when the dihedral angle is at -30^o. The most stable conformation of Compound 7 obtained from the PM6 method can be seen here:

Hence, since C=O lies below the ring where there is large steric hindrance, aniline would preferentially attack from the top, hence resulting in the stereochemistry observed in Compound 8. This is supported by literature, where the nucleophile attacks the opposite face of the carbonyl group due to steric considerations.

The models used in these calculations could be improved by using DFT-based molecular orbital methods as well as making use of a system which contain more recorded elements such as Mg.

Stereochemistry and Reactivity of Intermediate in Synthesis of Taxol

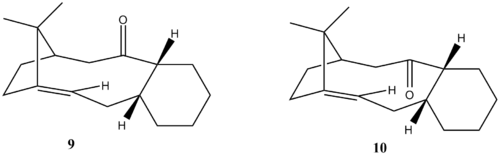
In the total synthesis of Taxol proposed by Paquette, a key intermediate (either 9 or 10) is synthesised with the carbonyl group pointing either up or down. On standing, the compound isomerises between the alternative carbonyl isomers, 9 and 10, which are atropisomers with chirality about the axis. Intermediates 9 and 10 were sketched in ChemBio3D and optimised using both the MM2 and MMFF94 methods.

Figure 7:Intermediates of Taxol

It was noted that the 6-membered ring of the initial optimised structure of both intermediates were incidentally in a boat conformation. As a chair-conformation is typically the more stable conformation for a 6-membered ring, the structure of the 6-membered ring was manually twigged into a chair conformation and optimised again. The optimised structure of intermediates 9 and 10 can be viewed here: The energies of intermediates 9 and 10 are presented in tables 5 and 6 below.

Table 5: Relative Energies of Intermediates 9 and 10 (Using MM2 force-field)

	Energies/ kcal mol-1						Energies/ kJ mol-1
	Stretch	Bend	Torsion	Van der Waals	Dipole-Dipole	Total	Stretch	Bend	Torsion	Van der Waals	Dipole-Dipole	Total
Intermediate 9a (Boat)	2.79	16.48	20.62	13.84	0.17	54.13	11.66	68.93	86.29	57.90	0.72	226.46
Intermediate 9b (Chair)	2.69	15.87	18.20	12.63	0.14	48.90	11.24	66.38	76.15	52.86	0.61	204.61
Intermediate 10a (Boat)	2.65	11.24	21.83	13.59	-0.19	48.16	11.08	47.05	91.33	56.85	-0.80	201.51
Intermediate 10b (Chair)	2.56	10.69	19.74	12.54	-0.18	44.29	10.73	44.74	82.58	52.46	-0.76	185.31

Table 6: Comparison of Results from MM2 and MMFF94 Force Field

	Total Energy of Intermediate
	MM2/ kcal mol-1	MMFF94/ kcal mol-1	MM2/ kJ mol-1	MMFF94/ kJ mol-1
Intermediate 9a (Boat)	54.13	77.94	226.46	326.12
Intermediate 9b (Chair)	48.90	70.54	204.61	295.14
Intermediate 10a (Boat)	48.16	66.34	201.51	277.58
Intermediate 10b (Chair)	44.29	60.56	185.31	253.38

It can be seen that molecules with the 6-membered ring in a chair conformation is indeed more stable than that in a boat conformation. Also, it is observed that both the MM2 and MMFF94 methods show that intermediate 10 is the energetically more stable intermediate. This supports the experimental observation where the compound isomerises to intermediate 10 on standing. As can be seen from intermediates 9 and 10, the 2 transannular hydrogens are pointing upwards. Hence, when the C=O is pointing upwards as is the case for intermediate 9, a large transannular strain is observed; conversely, when the C=O is pointing downwards in intermediate 10, such a strain is avoided. Hence, comparing the most stable conformations of intermediates 9 and 10, intermediate 10 is more stable than intermediate 9 by 19.30kJ mol^-1 using the MM2 method and 41.76 kJ mol^-1 using the MMFF94 method.

Although both the MM2 and MMFF94 methods give similar trends in terms of the stability of the intermediates, it is important to note that the difference in energies between the two intermediates is almost two times larger when the MMFF94 method is used as compared to when the MM2 method is employed. One of the most important differences between MMFF94 and MM2 force fields lies in their description of non-bonded interactions. MMFF94 uses a novel “buffered” expression to describe Van der Waals interactions; in particular, Van der Waals interactions involving aliphatic hydrogens is parameterized using high quality ab initio data and non-bonded interactions in polar systems are parameterized using HF/6-31G* calculations on hydrogen-bonded complexes. As a result, studies have shown that MMFF94 force fields can produce appropriate trends in the HF/6-31G* data fairly well. In addition, the intermolecular interaction energies and geometries obtained using the MMFF94 method is very similar to that obtained using the highly regard OPLS force field. On the other hand, MM2 potential fare rather poorly as it is much too stabilizing the region of the Van der Waals minima.^, As the difference in energies between intermediates 9 and 10 largely stems from absence or presence of the interactions between the oxygen and hydrogen atoms, the MM2 method probably underestimated the destabilisation energy of the non-bonded interactions, hence resulting in a small difference in energy between intermediates 9 and 10. The value obtained from MMFF94 is probably more accurate.

Taxol has been proposed to be a hyperstable alkene by C. S. Swindell et al. via MM2 calculations. Hyperstable alkenes are unreactive olefins which are less strain than their parent hydrocarbon and possess negative olefin strain values. It is also noted that strain caused by bridgehead olefins can be relieved with increasing ring size, hence the double bond observed in Taxol is in the larger ring rather than the smaller one as seen in Figure 7 above. It is interesting to note that generally, the unreactivity of hyperstable alkenes is not attributed to steric hindrance or enhanced pi-bond strength; instead, the unreactivity is due to the special stability afforded by the cage structure of the olefin and to the greater instability of the parent polycycloalkane. MM2 calculations were peformed on intermediates 9c and 10c, where the alkene bond in 9b and 10b were substituted with a single bond respectively. The results are shown in table 7 below, illustrating the fact that the alkene olefin is more stable.

Table 7: Comparison of Intermediates 9b with 9c and 10b with 10c, where the alkene bond was substituted with a single bond

	Energies/ kcal mol-1	Energies/ kJ mol-1
Intermediate 9b (Chair)	48.90	204.61
Intermediate 9c (Chair)	51.87	217.01
Intermediate 10b (Chair)	44.29	185.31
Intermediate 10c (Chair)	56.62	236.89

Regioselective Addition of Dichlorocarbene

Orbital Control

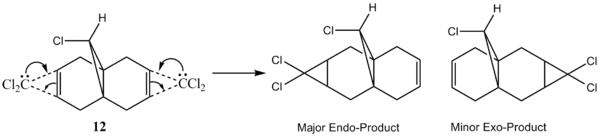
The reaction of 12 with dichlorocarbene results in an addition to the syn C=C bond (which is the C=C bond close to Cl), yielding the endo product as the major product (72%). Addition to the anti C=C bond leads to the formation of the exo product, which is the minor product (23%).

Figure 8: Endo and Exo Products of Reaction between Dichlorocarbene and 12

Figure 9: HOMO-1 and HOMO Orbitals

HOMO-1	HOMO

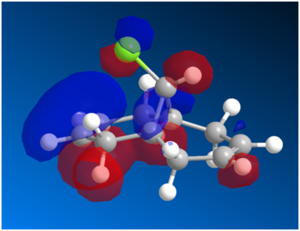While the HOMO-1 orbital shown on the left shows large electron clouds residing over both the syn C=C bond and anti C=C bond, the HOMO orbital consists mainly of a much larger electron cloud residing over the syn C=C bond as compared to that of the anti C=C bond. As the HOMO is presumed to be the most reactive towards electrophilic attack, the distribution of electron cloud suggests that the syn C=C bond is much more susceptible to electrophilic attack as compared to the anti C=C bond. In addition, as the electronegative Cl is in closer spatial proximity to the syn C=C bond than the anti C=C bond, it renders the syn C=C bond more electron deficient, hence making it more nucleophilic. As the reaction of 12 with dichlorocarbene is similar to electrophilic addition, the dichlorocarbene preferentially attacks the much more nucleophilic syn C=C bond. This is in line with experimental observations, where the endo product is the major product observed.

Figure 10: LUMO, LUMO+1 and LUMO+2 Orbitals

LUMO	LUMO+1	LUMO+2

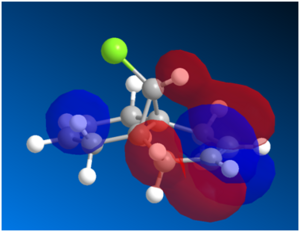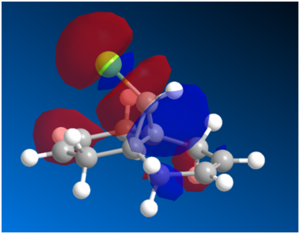The LUMO+1 shown above consists mainly of the σ*(C-Cl) orbital whereas the HOMO-1 consists of a π(C=C) anti-alkene orbital. Based on literature, interaction of the LUMO+1 with the HOMO-1 would lead to an antiperiplanar stabilisation, which would lower the energy of the molecular orbitals for the anti-alkene. This would render the syn-alkene more reactive, hence yielding the endo-product. Although the PM3 method is used in literature whereas the PM6 method is used for this calculation, the results from both method should be comparable. While the difference in parameterisation of H-bonding in PM6 and PM3 might have an effect on the overall stabilisation energy of the molecule, the trend observed where the energy of the molceular orbitals for the anti-alkene is more stable than that of the syn-alkene should still remain.

Hence, it has been shown through the study above that, by considering the HOMO and LUMO orbitals using the PM6 method, the syn and anti C=C bond can be discriminated from one other.

Vibrational Frequency

Figure 11: Compounds 12 and 13

The optimised structures of compounds dialkene 12 and monoalkene 13 can be viewed here:

Table 7: Comparison of Vibrations of 12 and 13

	Literature Values	12 DOI:10042/to-6386	13 DOI:10042/to-6458
IR Spectra	-
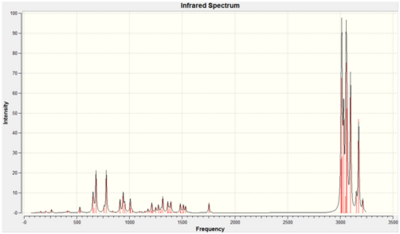C=C (syn)/ cm-1	1745	1757.45	1753.76
C=C (anti)/ cm-1	1745	1737.08	-
C-Cl/ cm-1	760-505	770.84	779.93

As the key functional groups in 12 and 13 are the C-Cl and C=C bonds, only the C-Cl, C=C (syn) and C=C (anti) stretches are compared in table 7 above, ignoring the C-C and C-H bends and stretches. Both the C-Cl frequencies correspond rather closely to literature values, where a C-Cl stretch lies typically around 760-505cm^-1. Dialkene 12 has two C=C stretches at 1757.45cm^-1 and 1737.08cm^-1 which corresponds to the syn C=C bond and anti C=C bond respectively. Only one C=C stretch at 1753.76cm^-1 is observed for monoalkene 13. Based on literature values, cyclohexene with electron withdrawing fluorine groups has a C=C stretch at 1745cm^-1 whereas normal cyclohexene has a C=C stretch at ~1645cm^-1. Hence, the presence of the electronegative Cl would render the C=C stretches much higher than 1645cm^-1 and closer to 1745cm^-1. This is seen in the assignment of frequencies of the anti and syn C=C stretches, where the syn C=C bonds which are in closer proximity with Cl have a higher frequency of 1757.45cm^-1 and 1753.76cm^-1 in dialkene 12 and monoalkene 13 respectively, whereas the anti C=C bond which is further away from the Cl in dialkene 12 has a lower frequency of 1737.08cm^-1. In addition, another reason to account for the fact that the anti C=C stretch of 1737.08cm^-1 is higher than the usual 1645cm^-1 is that the σ*(C-Cl) orbital interacts π(C=C) anti-alkene orbital as described in the previous part, hence lowering the energy of the anti C=C bond, resulting in a stronger bond with a higher vibrational frequency. The lower stretching frequency of the anti C=C bond implies that it is a weaker bond as compared to the syn C=C bond. Hence, hydrogenation occurs at the anti C=C bond and not at the syn C=C bond, as shown in monoalkene 13.

Structure-Based Mini-Project: Domino Michael-Henry Reaction

Introduction

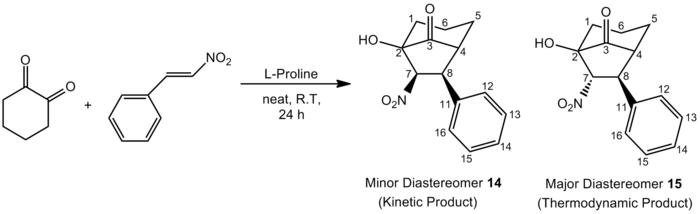
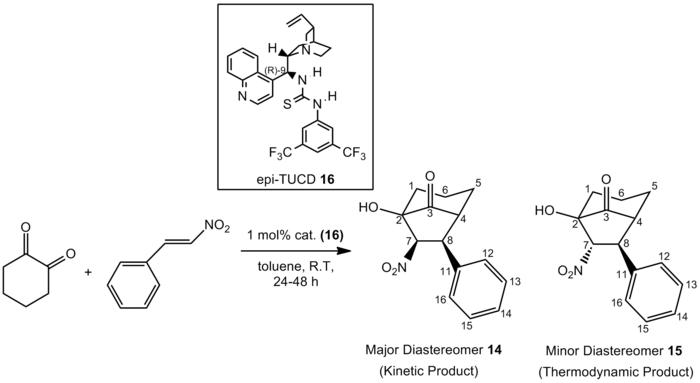
It has been reported that 1,2-diones would undergo a Michael addition to nitroalkenes, followed by an intramolecular Henry reaction to give bicycles. The two reaction schemes presented in figures 12 and 13 below (obtained from two different papers^,) both illustrate the domino Michael-Henry reaction, where cyclohexa-1,2-dione reacts with β-nitrostyrene, yielding two diastereomers in different ratios. In the absence of catalyst 16, the thermodynamic product is the major product observed, where the diastereomeric ratio of compound 14:compound 15 is 1:9. However, in the presence of catalyst 16, the diastereomeric ratio is reversed, where the diastereomeric ratio of compound 14:compound 15 is now 3.3:1 and the kinetic product becomes the major product observed.

Figure 12: Domino Michael-Henry Reaction Without Catalyst

Figure 13: Domino Michael-Henry Reaction With Catalyst 16

The optimised structures of compounds 14 and 15 can be viewed here:

Proposed Mechanism

For the first reaction scheme shown in Figure 12, F. Felluga et al. proposed the following mechanism where L-proline first reacts with cyclohexa-1,2-dione. The resultant cross-conjugated enaminone then reacts with β-nitrostyrene via Michael-addition, followed by an intramolecular Henry reaction to eventually give the two diastereomers 14 and 15. In this reaction where no catalyst is used, the thermodynamic product 15 is the major diastereomer produced.

Figure 14: Reaction Mechanism of Domino Michael-Henry Reaction Without Catalyst

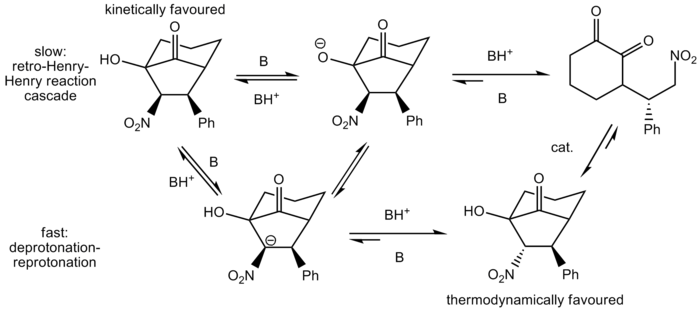
Such an observation is supported by M. Rueping et al. where the use of 0.5 mol% also favoured the formation of the thermodynamic product 15. Nevertheless, when 1 mol % of catalyst 16 was used, the formation of the kinetic product 14 was favoured. M. Rueping et al. hence proposed a base-catalysed epimerization mechanism to account for the observation where the thermodynamic product is the major diastereomer. As can be seen in the mechanism shown below, both a slow retro-Henry-Henry reaction cascade and a fast deprotonation-reprotonation reaction would lead to the formation of the thermodynamic product.

Figure 15: Base Epimerization Mechanism

¹³C NMR

Both diastereomers 14 and 15 were first sketched in ChemDrawPro and ChemBio3D where the 6-membered ring was drawn in a chair conformation. This was because it was observed in the study of Taxol that an overall more stable molecular conformation is obtained when the 6-membered ring is in a chair conformation as compared to a boat conformation. The diastereomers were then optimised first using MM2, followed by the DFT method mpw1pw91 using the 6-31G(d,p) basis set. The output files were checked to ensure that both the force and displacement have converged, hence a minimum energy is obtained. In addition, the optimised geometry was opened in Gaussview to ensure that the molecule has not disintegrated. Based on the optimised structures, the ¹³C NMR spectra were then predicted for both diastereomers in chloroform (solvent used by F. Felluga et al.) and in dichloromethane (solvent used by M. Rueping et al.). The results are presented in tables 8 and 9 below.

Table 8: Comparison of NMR Results from Literature and Predicted Values

Carbon Assignment	Literature δ of Major Diastereomer 15/ ppm	Predicted δ of Major Diastereomer 15/ ppm DOI:10042/to-6462	Literature δ of Minor Diastereomer 14/ ppm	Predicted δ of Minor Diastereomer 14/ ppm DOI:10042/to-6461
C-3	212.5 (s)	215.5	213.9 (s)	214.9
C-11	142.3 (s)	141.1	136.3 (s)	134.2
Aromatic Carbons C-12 to C-16	129.4 (2d)	121.9 (C-16)	128.7 (2d)	127.8 (C-12)
	127.8 (d)	124.1 (C-14)	128.5 (2d)	125.9 (C-16)
	126.7 (2d)	125.4 (C-13)	127.8 (d)	125.2 (C-15)
		126.3 (C-15)		124.5 (C-13)
		125.5 (C-12)		124.9 (C-14)
C-7	93.6 (d)	94.7	91.0 (d)	91.0
C-2	81.6 (s)	81.6	80.0 (s)	80.7
C-4	51.6 (d)	52.3	47.1 (d)	50.5
C-8	43.9 (d)	45.0	44.3 (d)	47.4
C-1	39.8 (t)	40.6	41.2 (t)	41.3
C-5	36.0 (t)	37.6	35.9 (t)	37.0
C-6	17.9 (t)	19.7	17.6 (t)	19.3

Table 9: Comparison of Predicted NMR Results from Literature

Carbon Assignment	Literature δ of Mixture/ ppm	Integral	Predicted δ of Major Diastereomer 14/ ppm DOI:10042/to-6459	Predicted δ of Minor Diastereomer 15/ ppm DOI:10042/to-6460
C-3	213.8	4	215.4	215.2
-	184.6	3	-	-
C-11	142.5	2	-	141.0
	136.7	6	134.4	-
Aromatic carbons C-12 to C-16	129.2	Multiplet on NMR Spectrum was too small to be integrated.	127.8 (C-12)	-
	128.7		125.9 (C-16)	126.3 (C-15)
	128.3		125.1 (C-15)	125.5 (C-12)
	128.0		124.9 (C-14)	125.4 (C-13)
	127.6		124.6 (C-13)	124.1 (C-14)
	126.7		-	121.9 (C-16)
C-7	93.7	5	-	94.7
	91.2	16	91.1	-
C-2	81.7	1	-	81.7
	80.1	3	80.8	-
C-4	51.9	9	50.7	52.5
C-8	47.1	21	47.4	-
	44.0	7	-	45.2
-	44.2	18	-	-
C-1	41.4	26	41.3	40.7
-	39.9	10	-	-
C-5	36.2	11	-	37.7
	36.0	27	37	-
C-6	18.1	26	-	19.7
	17.7	9	19.3	-

As the NMR results presented by F. Felluga et al. were for each individual diastereomer, assignment of the NMR peaks was made much easier. However, no integrals was presented by F. Felluga et al. and no image of the spectrum was provided as well, hence no integrals was presented in table 8 above.

The NMR spectrum presented in the paper by M. Rueping et al. is for the diastereomeric mixture, not the individual separated diastereomers. In addition, the assignment of the NMR peaks to their respective carbons was not presented. Nevertheless, such assignments could be made as shown in table 9 by simply comparing the predicted values from the calculations to the experimental values as well as comparing the integral of the peaks to the ratio of diastereomers obtained. It should be noted that the literature integrals presented in the table above are all measured manually by hand, because only an image of the NMR spectrum was provided with no integrals presented in the paper. In addition, the assignment of peaks to carbons can be compared with that presented by F. Felluga et al. as well. Although different solvents were used in the two papers, the predicted chemical shifts were still rather similar.

Referring to the results presented by M. Rueping et al., two peaks observed next to each other in the ratio of 1:3 usually represent the same carbon in the two diastereomers. This is the case for C-7 (which NO₂ is directly attached to), C-2 and C-8 (which are carbons right next to C-7), C-11 (which is in very close special proximity to the NO₂ group in diastereomer 14) and C-6 (which is in very close special proximity to the NO₂ group in diastereomer 15). Only one peak is observed for C-1, C-3 and C-4 instead of two peaks in the ratio of 1:3 because they are at least 2 carbons or more away from C-7, hence the effect of diastereoisomerisation is not felt greatly. Although 2 peaks in the ratio of 1:3 is still observed for C-5 (which is 3 carbons away from C-7), the difference between the two peaks is actually very small (less than 0.2ppm). Three of the NMR peaks presented by M. Rueping et al. at 184.6ppm, 44.2ppm, 39.9 ppm could not be assigned to specific carbon atoms. They could possibly represent impurities in the mixture as those peaks are not present in the NMR results presented by F. Felluga et al.

As can be seen from both tables 8 and 9 above, the predicted values correspond very closely to that of literature values^,. Generally, ¹³NMR is a good method to distinguish between two different diastereomers as atoms in different diastereomers would possess different chemical environments which would result in different chemical shifts. The key difference between the NMR spectra of diastereomers 14 and 15 lies in the chemical shift of C-11(shown in red text), where the NO₂ group points out of the plane in the same direction as C-11 in diastereomer 14 but into the plane in the opposite direction in diastereomer 15. This results in a difference of about 7ppm observed.

IR Spectrum

It is expected that IR spectroscopy would not be very useful in differentiating between diastereomers 14 and 15 as both diastereomers have the same functional groups present. Nonetheless, IR spectra were still predicted for both diastereomers 14 and 15 and the results obtained for both diastereomers 14 and 15 were indeed very similar. As the prediction of IR spectra is not useful in distinguishing between the diastereomers in this case, the results are not presented here.

However, based on the output, it is observed that product 15 is approximately 10.94 kJ mol^-1 more stable than product 14. This is in line with the fact that product 14 is the kinetic product whereas product 15 which is more stable is the thermodynamic product.

Optical Rotation

Table 9: Comparison of Optical Rotation Results from Literature and Predicted Values

Basis Set	Literature	Major Diastereomer 14	Minor Diastereomer 15
aug-cc-pvdz	+49.1	+14.98	+17.81
6-311G(d,p)	+49.1	+9.13	+27.62

Optical rotation would be useful in the differentiation of enantiomers as it will give a positive value for one and a negative value for the other enantiomer. However, optical rotation is not as useful in differentiating diastereomers, which can be seen here.

As the prediction method used is only reliable for [α]_D values greater than 100^o, the experimental literature value of 49.1^o cannot be accurately predicted. Even when an augmented polarization basis set aug-cc-pvdz is used, the values predicted are very different from the experimental values.

Conclusion

Molecular mechanics provides a simple way of optimising the geometry to an energy minimum. As seen from the exercises performed above, the energy can then be analysed to predict accurately whether a reaction is kinetically controlled (as in the dimerisation of cyclopentadiene) or thermodynamically controlled (as in the hydrogenation of cyclopentadiene dimer). It can also be used to identify the energetically more stable intermediate in reactions such as the synthesis of Taxol. Different molecular mechanics methods would give slightly different results as well, although the trend may tend to be similar.

While molecular mechanics methods are useful, they do not explicitly take into consideration the effects of orbitals and electrons which often influence the reactivity of bonds and spectroscopic properties of a molecule. This is seen in the regioselective addition of dichlorocarbene, where the syn C=C bond is more susceptible to electrophilic attack whereas the anti C=C bond preferentially undergoes hydrogenation.

Through the study of neighbouring group participation of C-Cl and C=C stretching frequency of the chloro-substituted bicyclic diene as well as a mini-project involving a domino Michael-Henry reaction, DFT-based molecular orbital methods have proven to be very useful in the prediction of spectroscopic properties. Analysis of the predicted spectrums can lead to useful information such the differentiation between diastereomers.