Rep:Mod:wqt14

A Study of Transition State and Reactivity using Computational Methods

Understanding Potential Energy Surfaces (PES)

The plotting of PES is one of the most effective methods to graphically conceptualise the variations in energy of the reaction system as the molecular structures change, generating crucial information on the molecular properties and the nature of the reaction.

The critical points on a PES are the minima and first-order saddle point. The minima corresponds to the molecular structure at equilibrium, while the first-order saddle points corresponds to the transition state structure. Both points are stationary points, where the first derivative of energy with respect to nuclear coordinates equals to zero. Due to the fact that the negative of the first energy derivative is equivalent to the force, there are no forces acting at these points as well.

By calculating the Hessian (i.e. second energy derivative), one can deduce the local curvature of the PES and use it to determine the nature of the stationary points. At the minimum, the second derivative will be more than zero, while at the transition state (first-order saddle point), the second derivative will be less than zero. From the proportional relationship between vibrational frequency and the the square root of the eigenvalues of the mass-weighted Hessian, a convenient means to check whether or not the optimised structure is a minimum or a transition state would be to run a frequency calculation: there will be no negative frequencies at minima points, while there will be exactly one negative frequency at the point corresponding to the transition state.

In a reaction, the chemical system transits from a minimum corresponding to the reactants, to another minimum corresponding to the products, passing through points of highest energy that corresponds to transition states.
Nf710 (talk) 21:35, 8 March 2017 (UTC) This is a good understanding however there a few things you are missing. At a first order saddle point only one of the eigenvalues of the hessian will be negative. Secondly yes the hessian is with respect to nuclear coordinates, but in the normal mode basis (3N-6) rather than cartesian 3N.

Analysis of Reactions using Computational Chemistry

Gaussian and GaussView are the computational Chemistry program and graphical user interface used respectively. The two electronic structure methods applied are:
1) Semi-empirical method PM6: to obtain the initial geometry of the molecules.
2) Density Functional Theory (DFT) method B3LYP: to further optimise the geometry obtained from the semi-empirical method.

The molecular structure of the product will first be minimised to find the equilibrium geometry, ensuring that there are no negative frequencies in vibration calculations. After which, the structure of the product will be modified to reflect the transition state by deleting the bonds that form during the reaction, increasing the bond lengths between them and freezing the atoms involved. The modified structure is optimised to a minimum again, before running transition state optimisation to locate the first-order saddle point in the PES. The vibration calculation of the transition state is verified to have only one negative frequency. The vibration of the molecular structure at this imaginary frequency corresponds to the movement of the reaction system through the highest point along the PES. From the optimisation calculations, the barrier heights of different reaction pathways and the relative energies of the formed products can be obtained to understand which reaction pathway is kinetically and/or thermodynamically favoured. An intrinsic reaction coordinate (IRC) calculation can also be set up to visualise the reaction progress.

By monitoring the reaction progress via the IRC and visualising the molecular orbitals involved to form a transition state, a better understanding can be gained on how factors such as stereochemistry and orbital interactions can have a significant influence on the kinetics and thermodynamics of reactions.

Nf710 (talk) 21:41, 8 March 2017 (UTC) This section was good but it would have been good to show some understanding of the electronic structure methods rather than just stating them.

Cycloaddition

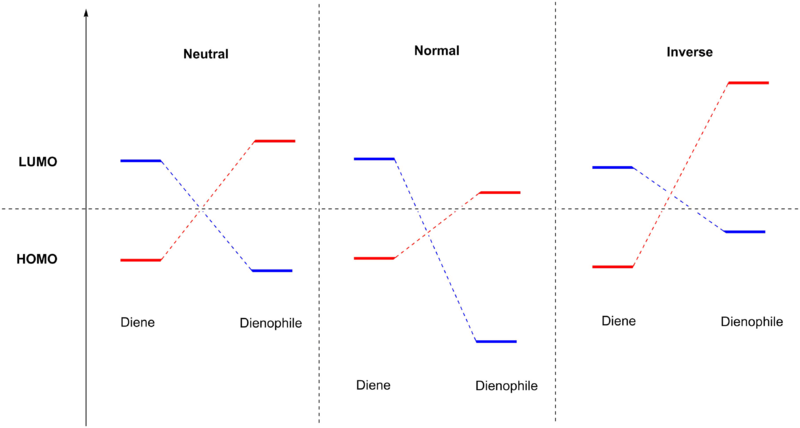
Cycloaddition reaction involves two σ bonds forming at the same time to generate a ring structure. The Diels-Alder reaction is specifically [4+2] cycloaddition which involves a conjugated diene reacting with an alkene functionality to give cyclohexene. By Woodward-Hoffman rules, the Diels-Alder reaction is an "orbital-controlled, thermally permitted and [a] concerted pericyclic reaction". Using the frontier molecular orbital theory, we can compare the relative energies of the HOMO and LUMO in the reactants and thus determine the interaction between the frontier orbitals responsible for bond formation. The Diels-Alder reaction can be categorised into normal, inverse and neutral electron-demand (Fig 1). In each case, the most significant interaction comes from the two orbitals that are closest in energy. For example, in the normal Diels-Alder reaction, the most significant interaction is between HOMO(diene) and LUMO(dienophile), while for the inverse Diels-Alder reaction, it is between HOMO(dienophile) and LUMO(diene). The two possible pairs of interaction are similar in the case of a neutral Diels-Alder reaction.

Fig 1: Three possible types of Diels-Alder reaction

Exercise 1: Reaction of Butadiene and Ethylene

Reaction Scheme

(Fv611 (talk) 12:44, 6 March 2017 (UTC) This is not the right product.)

Molecular Orbital (MO) Diagrams

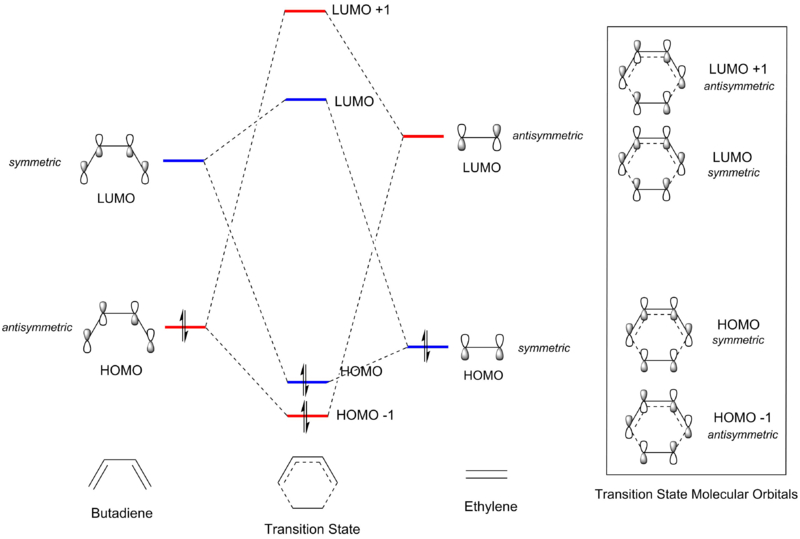
Fig 2: Schematic MO Diagram for Reaction between Butadiene and Ethylene

Table 1: Molecular Orbitals (jmol)
MO	Butadiene	Ethylene	Transition State
LUMO +1
LUMO
HOMO
HOMO -1

Symmetry Requirements

In Fig 2 and Table 1, MOs are determined to be symmetric or antisymmetric based on an imaginary mirror plane of reflection cutting through the central C-C bond of the molecule. From Fig 2, it can be seen that only MOs of the same symmetry can interact to generate a molecular orbital in the transition state. It can be inferred that for a reaction to be allowed, the interacting HOMO and LUMO from each reactant would need to have the same symmetry, i.e. the interaction has to be either symmetric-symmetric or asymmetric-asymmetric, where orbital overlap would be non-zero. Conversely, a reaction would be forbidden if the HOMO and LUMO required for bond formation between the two species are of opposite symmetries, and orbital overlap would be zero.

(Fv611 (talk) 12:44, 6 March 2017 (UTC) It would have been nice to have a formula for orbital overlap.)

Neutral Electron-Demand

This reaction can be categorised as a Diels-Alder reaction with neutral electron-demand, since the HOMO(ethylene)-LUMO(butadiene) energy gap is only slightly smaller than the HOMO(butadiene)-LUMO(ethylene) energy gap and both pairs of interaction contribute almost equally to the reactivity of the system.

Bond length Variations during Reaction

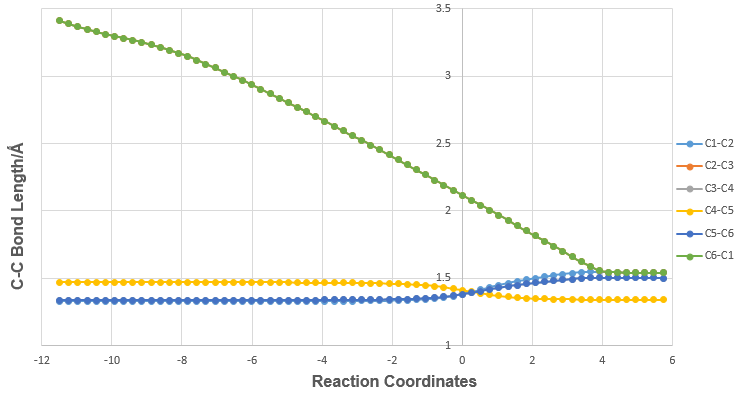
The variations in C-C bond lengths during the Diels-Alder reaction is as shown in Table 2 and Graph 1. The bond formation occurs at C₂-C₃ and C₆-C₁, which is why the bond lengths of C₂-C₃ and C₆-C₁ show a steady decrease as the butadiene and ethylene molecules move towards each other. The typical sp² C-C bond length is 1.34 Å, which is very similar to the bond lengths C₁-C₂, C₃-C₄ and C₅-C₆ in the reactants. In butadiene, C₄-C₅ is shorter than the typical sp³ C-C bond length of 1.54 Å, which demonstrates that the double bonds C₃-C₄ and C₅-C₆ are conjugated with each other. In the transition state, the bond lengths of C₂-C₃ and C₆-C₁ are 2.11 Å each. This is less than two times the Van der Waals radius of carbon, which is equals to 1.70 Å . In other words, C₂-C₃ and C₆-C₁ are in the midst of bond formation, where the bond lengths are in between the internuclear separation of two non-bonded carbons at 3.40 Å and a C-C single bond at 1.54 Å. The C-C bond lengths in the final product are all longer relative to the reactants, demonstrating that the double bonds have transformed into single bonds, except at C₄-C₅ where the single bond is converted to a double bond after the reaction. The bond lengths in the product are also in close agreement with literature values.

Table 2: C-C bond length variation during Diels-Alder Reaction
		C1-C2 / Å	C2-C3 / Å	C3-C4 / Å	C4-C5 / Å	C5-C6 / Å	C6-C1 / Å
	Reactants	1.33	3.41	1.34	1.47	1.34	3.41
	Transition State	1.38	2.11	1.38	1.41	1.38	2.11
	Product	1.54	1.54	1.50	1.34	1.50	1.54

(Fv611 (talk) 12:44, 6 March 2017 (UTC) There should be no bond length available for C2-C3 and C1-C6 in the reactants, as they are optimised on their own.)

Graph 1: C-C bond length variation during Diels-Alder Reaction

The bond formation is synchronous for this reaction, and has an imaginary frequency is at 948.52i cm^-1 (Fig 3):

Fig 3: Vibration Corresponding to Bond Formation

Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

Reaction Scheme

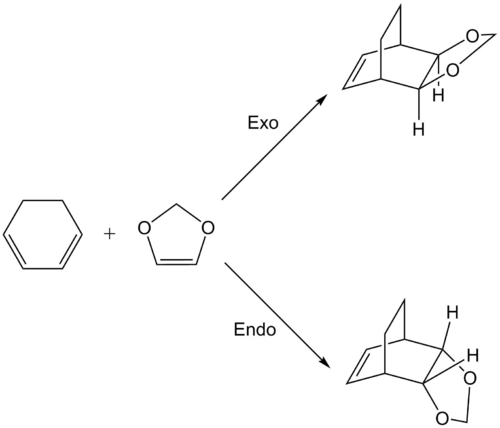
MO Diagrams

Fig 4: Schematic MO Diagram for Transition State Formation
Exo Transition State
Endo Transition State

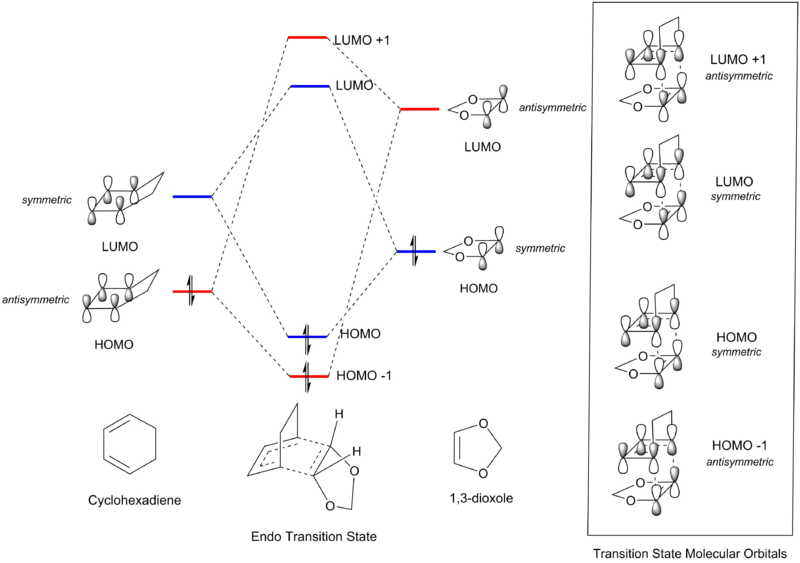Table 3: Molecular Orbitals (jmol)
MO	Cyclohexadiene	1,3-Dioxole	Exo Transition State	Endo Transition State
LUMO +1
LUMO
HOMO
HOMO -1

Inverse Electron-Demand

Due to the electron donating effect from the -O(C=O)O functionality, 1,3-dioxole is electron rich and thus its HOMO and LUMO are both higher than those from cyclohexadiene. This results in HOMO(1,3-dioxole)-LUMO(cyclohexadiene) energy gap to be significantly smaller than the HOMO(cyclohexadiene)-LUMO(1,3-dioxole) energy gap, resulting in a Diels-Alder reaction with inverse electron-demand.

The HOMO(1,3-dioxole)-LUMO(cyclohexadiene) symmetric-symmetric orbital overlap would be stronger than HOMO(cyclohexadiene)-LUMO(1,3-dioxole) antisymmetric-antisymmetric orbital overlap since the energies of the frontier orbitals are more similar in the former pair. However, the relative ordering of the MOs in the exo and endo transition states show that the HOMO-1 and LUMO+1 interactions still come from the antisymmetric-antisymmetric orbital overlap. This indicates that while the orbital overlap between HOMO(1,3-dioxole)-LUMO(cyclohexadiene) was quite large, it did not change the relative order of the MOs when compared to the transition state formed from the neutral Diels-Alder reaction seen in exercise 1.

Relevant Reaction Energies

Table 4 summarises the "Sum of Electronic and Thermal Free Energies" values under the "Thermochemistry" section in the .log file of the structures optimised using B3LYP calculations.

Table 4: Reaction Energies (in kJ mol-1) at 298 K
Position in PES	Compound	Energy/(Hartree per particle)	Total Energy/kJ mol-1	Relative Energy (to 2 d.p.)/kJ mol-1
Reactants	Cyclohexadiene	-233.324375	-1313780.62721	0.00
	1,3-Dioxole	-267.068132
Transition State	Exo	-500.329163	-1313614.31752	166.30
	Endo	-500.332152	-1313622.16514	158.46
Product	Exo	-500.417320	-1313845.77374	-65.15
	Endo	-500.418692	-1313849.37593	-68.75

The energy of the reactants is set to 0 kJ mol^-1 under the 'Relative energy' column, so that energy of the transition state would be equivalent to the height of the activation barrier and the relative thermodynamic stabilities of the exo and endo products can also be more easily compared.

The results show that endo transition state has a lower energy than the exo transition state, thus the activation barrier for the formation of endo product is smaller. The endo product also has a lower energy relative to the exo product. Therefore, the formation of the endo product is both kinetically and thermodynamically favoured.

Secondary Orbital Interactions

The endo pathway is more kinetically favourable due to the presence of secondary orbital interactions. Fig 5 shows the snapshots of the HOMO exo and endo transition states, as well as the schematic HOMO diagram including the oxygen orbitals. It can be seen that in the exo transition state, there are only primary interactions for bond formation, while in the endo transition state, the orbitals from oxygen (highlighted in red) can significantly interact with the orbitals from cyclohexadiene (highlighted in blue). The presence of secondary orbital interactions (highlighted as bold dotted curved lines) during the bond formation process stabilises the transition state, lowering the activation barrier for the formation of the endo product. This causes the endo pathway to be kinetically favoured.

Fig 5: HOMO in Exo and Endo Transition State
Exo	Endo

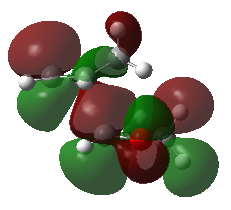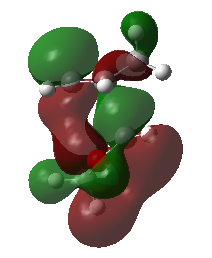Steric factors

Furthermore, the endo pathway is more thermodynamically favourable due to smaller steric repulsion in the final product. As can be seen in Fig 6, the highly unfavourable steric repulsion between the methylene groups causes the exo product to be much higher in energy relative to the endo product, thus the endo product is more thermodynamically stable.

Fig 6: Structure of Exo and Endo Products
Exo	Endo

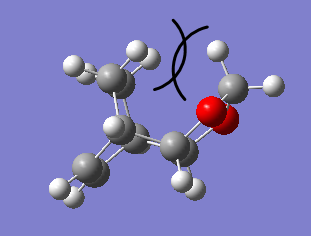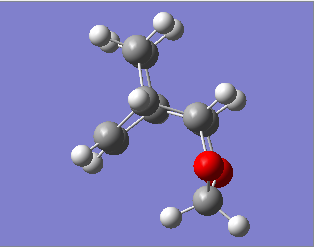Nf710 (talk) 21:50, 8 March 2017 (UTC) Your energies are correct and all your arguements are excellently complements with diagrams. Well done.

Exercise 3: Diels-Alder vs Cheletropic

Reaction Scheme

Reaction Pathways

O-xylylene is very unstable as it is anti-aromatic, having a planar structure with 8 π electrons. Due to this instability, the aromatic ring is generated before the bonds are formed with SO₂, as visualised in Fig 7. The steepest part of the PES in all reaction pathways corresponds to the restoration of aromaticity in the o-xylylene molecule, and the PES tapers off at the point when the bond formation occurs.

SO₂ is electron poor, thus its HOMO and LUMO are both lower than those from o-xylylene. Therefore, the most significant frontier orbital interaction is between HOMO(o-xylylene) and LUMO(SO₂) and the Diels-Alder reaction has a normal electron-demand. By restoring the aromaticity first, the reaction mechanism for the Diels-Alder pathways would proceed via a charge transfer-like mechanism, in the direction from the HOMO(o-xylene) towards the LUMO(SO₂). The SO₂ molecule induces opposite charges on each end of the cis-butadiene fragment, allowing aromaticity to be restored before the bond formation process. As a result, the bond formation process is asynchronous for exo and endo pathways, where the C-O bond forms ahead of the the C-S bond.

As for the cheletropic reaction pathway, in order to accommodate the restoration of aromaticity before bond formation, the HOMO(o-xylene) donates into LUMO(SO₂) simultaneously as the HOMO(SO₂) donates into LUMO(o-xylylene), in a manner analagous to σ bond donation/π back-donation in . The bond formation is synchronous, where C-S bonds form at the same time.

Fig 7: Exo, Endo and Cheletropic Reaction Pathways
Exo	Endo	Cheletropic

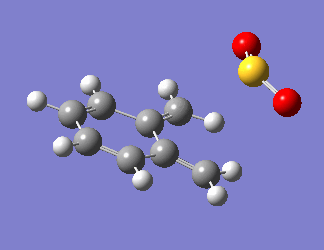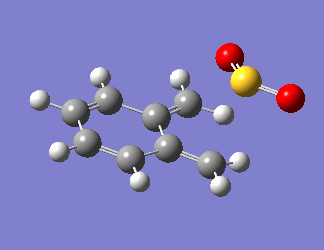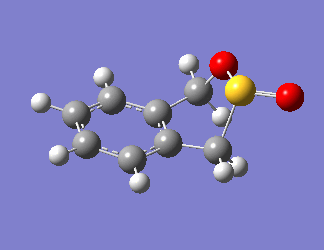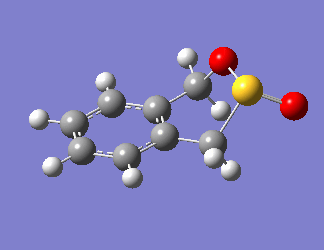Reaction Profiles

Table 5 summarises the "Sum of Electronic and Thermal Free Energies" values under the "Thermochemistry" section in the .log file of the structures optimised using PM6 calculations.

Table 5: Reaction Energies (in kJ mol-1) at 298 K
Position in PES	Compound	Energy/(Hartree per particle)	Total Energy/kJ mol-1	Relative Energy (to 2 d.p.)/kJ mol-1
Reactant	o-xylylene	0.177828	155.466369	0.00
	SO2	-0.118614
Transition State	Exo	0.092077	241.748182	86.28
	Endo	0.090560	237.765298	82.30
	Cheletropic	0.099062	260.087301	104.62
Product	Exo	0.021454	56.3274813	-99.14
	Endo	0.021695	56.9602268	-98.51
	Cheletropic	0.000005	0.013127501	-155.45

(Your energy for o-xylylene is a a bit high, but you have provided your log file and I can see it's just numerical noise Tam10 (talk) 12:11, 8 March 2017 (UTC))

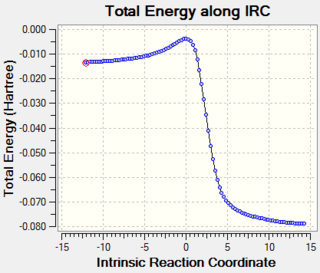
From the relative energy, we can plot a reaction profile of energy against reaction coordinates to graphically show the relative reaction barriers and the relative stabilities of the products formed from each pathway (Graph 2):

Graph 2: Reaction Profile for Exo, Endo and Cheletropic Reaction Pathways

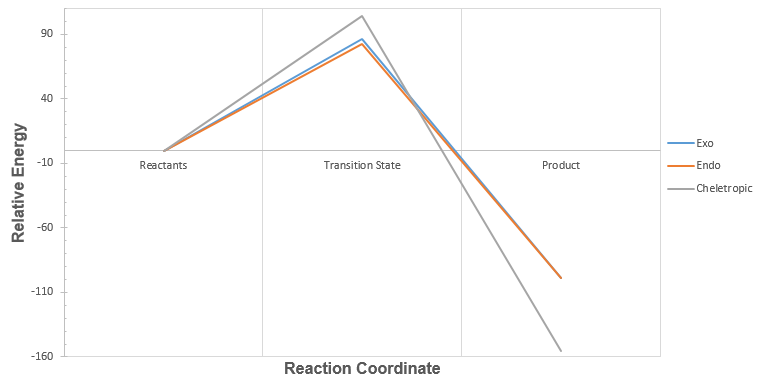From Table 5 and Graph 2, we can conclude that the endo pathway is the most kinetically favoured, while the cheletropic pathway forms the most thermodynamically stable product.

Kinetic and Thermodynamic Product

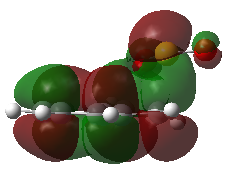
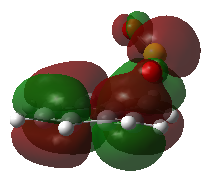
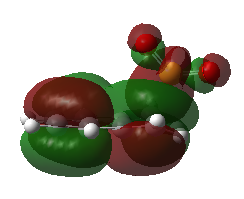
Fig 8 shows the HOMO of each of the transition state, and the structure of the products formed from each pathway. The endo pathway is most kinetically favoured as it is the only transition state where the oxygen orbital points to the orbitals in the carbons in the aromatic ring, for secondary orbital interaction. Although the secondary orbital interaction is not extensive, the endo transition state will be most stabilised out of the three pathways, causing the formation of endo product via Diels-Alder reaction to be kinetically favoured. The relative stability of the endo and exo product are similar, but the cheletropic product has a much lower energy. This shows that the five-membered ring is more thermodynamically stable than the Diels-Alder products. This conclusion agrees closely with literature, which had shown that the Diels-Alder products are unstable and readily undergo a retro-Diels-Alder reaction to yield the reactants. (Try to be more specific here as to what the literature is showing. They are inferring that under normal conditions, the DA products are not seen as the reaction is reversible Tam10 (talk) 12:11, 8 March 2017 (UTC))

Fig 8: Exo, Endo and Cheletropic Transition State and Product
Exo	Endo	Cheletropic

Alternative Reactive Site in O-Xylylene

There is a second cis-butadiene fragment in o-xylylene that can undergo a Diels-Alder reaction. Table 6 and Graph 3 show the reaction energies for a Diels-Alder reaction at this alternative reactive site.

Table 6: Reaction Energies at Alternative Site in O-Xylylene (in kJ mol-1) at 298 K
Position in PES	Compound	Energy/(Hartree per particle)	Total Energy/kJ mol-1	Relative Energy (to 2 d.p.)/kJ mol-1
Reactants	o-xylylene	0.177828	155.466369	0.00
	SO2	-0.118614
Transition State	Exo	0.105055	275.821924	120.36
	Endo	0.102070	267.984805	112.52
Product	Exo	0.067305	176.709291	+21.24
	Endo	0.065610	172.259068	+16.79

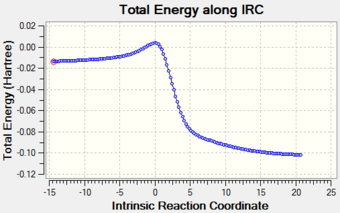
Graph 3: Reaction Profiles at Alternative Site in O-Xylylene

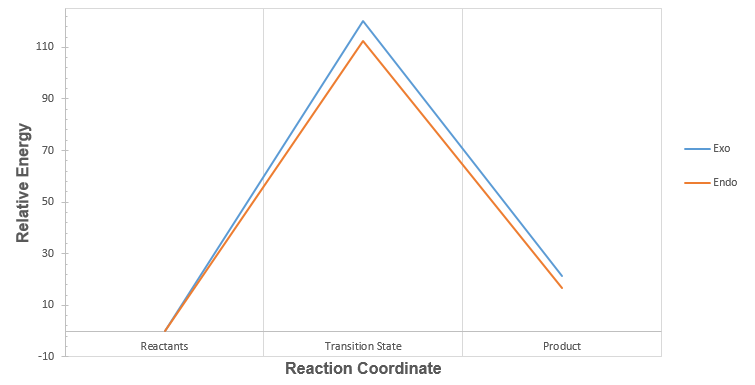For the exo and endo pathways, the activation barriers at the alternative reactive site (+120.36 kJ mol^-1 and +112.52 kJ mol^-1 respectively) (Table 6) are both larger than the activation barriers at the first cis-butadiene fragment (+86.28 kJ mol^-1 and +82.30 kJ mol^-1 respectively) (Table 5). Additionally, from Graph 3, it can be seen that both the exo and endo products formed at the alternative reactive site are higher in energy than the reactants. Therefore, the reaction at the second cis-butadiene fragment is both kinetically and thermodynamically unfavourable.

Conclusion

Plotting of the PES is a powerful method to compare the reaction barriers and relative stability of products between different pathways. In exercise 1 to 3, the Diels-Alder reaction was used as an excellent example of how orbital symmetry and steric factors can significantly affect reaction energies, with calculations obtained via PM6 and B3LYP calculation methods. Exercise 1 to 3 illustrate neutral, inverse and normal electron-demand Diels-Alder reaction respectively, providing a good range of the possible frontier orbital interactions. Exercise 1 shows that reactions are allowed only if the symmetry of the interacting HOMO and LUMO from each species are the same. Exercise 2 demonstrates factors that can determine the kinetic and thermodynamic products. The presence of secondary orbital interactions can stabilise transition states and lower the activation barrier to form the kinetic product, while steric repulsions can raise the energy of the product and cause it to be less thermodynamically favoured. Exercise 3 compares the exo and endo Diels-Alder and cheletropic reaction pathways, highlighting the important point that while the three mechanisms are concerted, the bond formation can be either synchronous or asynchronous depending on which product is formed. Exercise 3 also shows that not all reactive sites can give kinetically and thermodynamically favoured products.

Calculation Files

Ex 1

File:Ex 1 ethylene MO.log
File:Ex 1 butadiene MO.log
File:Ex 1 transition state MO.log
File:Ex1IRC.log

Ex 2

File:Ex 2 cyclohexadiene MO.log
File:Ex 2 dioxole MO.log
File:Ex 2 Exo TS jmol.log
File:Ex 2 Endo TS jmol.log
File:Ex 2 exoproduct.log
File:Ex 2 endoproduct.log
File:Ex 2 exoTS 631Gd IRC.log
File:Ex 2 endoTS 631Gd IRC.log

Ex 3

File:Ex 3 optmin xylylene.log
File:Ex 3 optmin SO2.log
File:Ex 3 Exo TS.log
File:Ex 3 Endo TS.log
File:Ex 3 Cheletropic TS.log
File:Ex 3 Exo Product.log
File:Ex 3 Endo Product.log
File:Ex 3 Cheletropic Product.log
File:Ex 3 Exo IRC.log
File:Ex 3 Endo IRC.log
File:Ex 3 Cheletropic IRC.log
File:Ex 3 Part 2 Exo TS.log
File:Ex 3 Part 2 Endo TS.log
File:Ex 3 Part 2 Exo Product.log
File:Ex 3 Part 2 Endo Product.log