Rep:Mod:woodfordreserve
Organic Computational Chemistry - Part 1 - Set Studies
Modelling Using Molecular Mechanics
Introduction
As an introduction to computational methods in chemistry, a molecular modelling technique will be utilised to achieve the following:
Use molecular mechanics to predict the geometry and regioselectivity of:
- The hydrogenation of cyclopentadiene dimer
- The stereochemistry of nucleophilic addition to two different pyridinium (NAD+ analogues)
- The conformation/atropisomerism of a large ring ketone intermediate in one synthesis of the anti-cancer drug Taxol
- The conformational preferences leading to dramatic (enzyme-like) acceleration of peptide hydrolysis[1]
The 1st postulate of quantum mechanics states that any information of particles in a system can be found using the position of the particle (r), their wavefunction (Ψ) and the correct operator (for example the Hamiltonian Ĥ). However it is accepted that certain properties can be modelled to a certain degree of accuracy accurately using classical mechanics. The Molecular modelling applies individual additive properties of bonds and atoms together, to obtain information about the molecule. As much as molecular modelling has its limitations, it has one distinct advantage over the valuable method of solving the Schrodinger equation; it is less heavy on CPU time.[2]
The 5 terms that are used in the MM approach are:
- The sum of all diatomic bond stretches (each expressed as a simple Hookes law potential).
- The sum of all triatomic bond angle deformations (also a simple Hookes law potential)
- The sum of all tetra-atomic bond torsions (a cosine dependance)
- The sum of all non-bonded Van der Waals repulsions (using a simple 6/12 potential).
- The sum of all electrostatic attractions of individual bond dipoles.
We assume that these properties don't interact/affect each other, and so (as mentioned above) are additive and give an energy of the molecule. As can be see, the above 5 terms rely on classically expressed properties including stretching force constants and bond dipole moments, and then by varying parameters such as bond angles, lengths and torsional angles, using established algorithms a geometric conformation of the molecule is achieved that results in a minimisation of the total energies, with each indivudual parameter staying within allowed boundaries (ie. a bond length that is below the length at which dissociation would occur). [2]
Note Reagarding MM2 Optimisations
Please note that in all cases, the RMS value required for termination of the minimisation calculation in ChemBio3D has been reduced to 0 (to give a better lowering of energy).
The Hydrogenation of the Cyclopentadiene Dimer
A well known property of cyclopentadiene its tendency towards spontaneous dimerisation through a [п4s+п2s] cycloaddition reaction under thermal conditions via the Hückel intermediate, to dicyclopentadiene, hence the need to "crack" the dimer prior to its use in synthtetic chemistry.
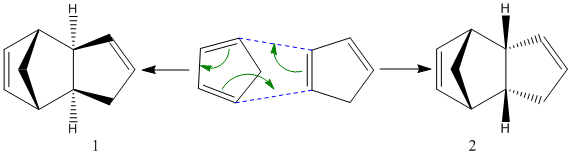
This cycloaddition gives the possibility of an exo (1) and endo (2) configurational isomer of the dimer. The endo dimer is the preferred shape, and can then be hydrogenated to give regioisomers (3) or (4).
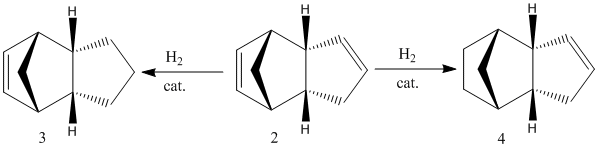
Further prolonged hyderogenation gives the tetrahydrogenated product (which will not be studied here). Energy minimising calculations using the MM2 force field model in ChemBio3D Ultra have been run to investigate whether the preference for the endo conformer is for kinetic or thermodynamic reasons.
The above files were initially created using ChemBio3D, and the in which the Allinger MM2 force field model based calculations are run.
| Contribution Parameter (all in kcal/mol) | Molecule 1 Exo Dimer | Molecule 2 Endo Dimer | Molecule 3 First Dihydrogenated Endo Dimer | Molecule 4 Second Dihydrogenated Endo Dimer |
|---|---|---|---|---|
| Stretch | 1.2851 | 1.2508 | 1.2778 | 1.0965 |
| Bend | 20.5805 | 20.8476 | 19.8588 | 14.5243 |
| Stretch-Bend | -0.8381 | -0.8358 | -0.8345 | -0.5494 |
| Torsion | 7.6555 | 9.5110 | 10.8109 | 12.4974 |
| Non-1,4 VDW | -1.4174 | -1.5439 | -1.2228 | -1.0700 |
| 1,4 VDW | 4.2333 | 4.3201 | 5.6328 | 4.5126 |
| Dipole/Dipole | 0.3775 | 0.4476 | 0.1621 | 0.1406 |
| Total Energy | 31.8764 | 33.9975 | 35.6850 | 31.1520 |
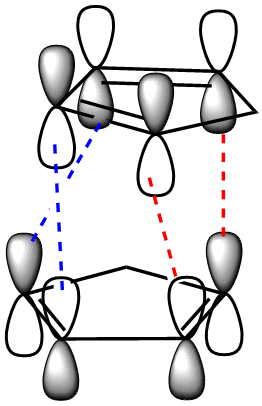
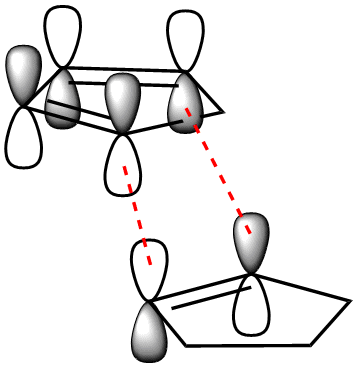
To begin with, we can see that the exo configuration (1) has a lower energy than the endo configuration (2), meaning that thermodynamically it is the less strained. The predominant endo configration is therefore the kinetic product, and the exo product the thermodynamic product. Through understanding the frontier MO interactions of the cycloaddition in the transition state, we can better understand the reason for the preference of the endo product over the exo. The requirement for the bonds being formed in the diels alder reaction is the interaction between the diene C1 and C4 p orbitals, and the p orbitals of the dieneophile (red).
Dihydrogenation of the endo dimer leads to one of two regioisomers (3) and (4) (above). Product (4) has the lower total energy, and hence it is thermodynamically more stable and more easily synthesised. The difference in energy between the two products is largely accounted for by the energy caused by bending of the molecule due to strain in the ring with the remaining doule bond. To clarify the cause of this energy increase, the bond angles of the carbons on the double bond were measured. For molecule (3) the angle at both carbons was found to be 107.6°, and for molecule (4); 112.4° and 113°. These, when compared to the optimum bond angle for an sp2 carbon of 120°, show that there is a larger amount of strain in molecule (3) due to the larger deviation from the optimum angle.
Stereochemistry of Nucleophilic Additions to a Pyridinium Ring (NAD+ Analogue)
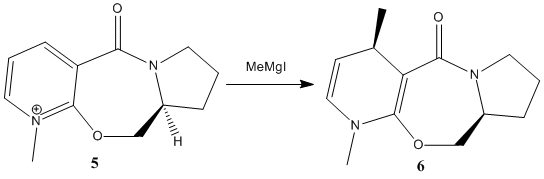
The proline (an amino acid) derivative prolinol (5) reacts with the gringnard reagent methyl magnesium iodide to alkylate the pyridine ring in the 4-position, with the absolute stereochemistry shown in (6). To rationalise this high level of stereoselectivity a 3D model of the reactant prolinol was created in ChemBio3D and minimised using the MM2 force field. After several successive inspections and minimisations (to ensure that a local thermodynamic minima conformation is not being analysed, rather than the abosolute minima), the geometry and orientation of the carbonyl group with respect to the aromatic ring was analysed.
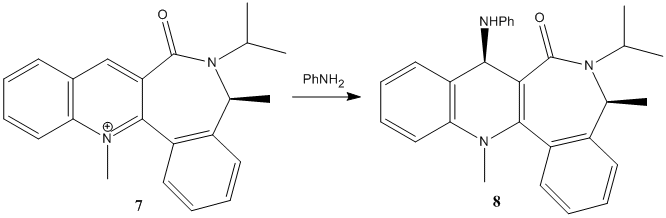
In the second study, the pyridinium ring (7) is reacted with aniline to form the derivative(8), with it's own stereoselectivity. For this reaction of the pyridinium ring (7) with PhNH2, a simialar analytical procedure to that described above was used.
The lowest energy results for molecules 5 and 7 were:
| Contribution Parameter (all in kcal/mol) | Prolinol (5) | Pyridinium Ring (7) |
|---|---|---|
| Stretch | 1.1779 | 1.5410 |
| Bend | 11.4235 | 6.7144 |
| Stretch-Bend | 0.0440 | 0.3378 |
| Torsion | 5.0844 | 5.7685 |
| Non-1,4 VDW | -1.9644 | -2.6620 |
| 1,4 VDW | 11.9160 | 13.2855 |
| Charge/Dipole | 2.6661 | 2.3476 |
| Dipole/Dipole | -3.9843 | -4.8270 |
| Total Energy | 26.3632 | 15.1919 |
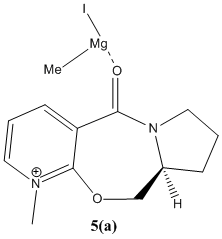
When the reactant (5) was run with the gringnard reagent MeMgI, the error "WARNING! No atom type was assigned to the selected atom." was seen. This error indicates that the relevant force field values for Mg needed for the calculations are not available in the MM2 set, as can be seen in the literature. [3]
[4]
Inspection of the dihedral angle of the carbonyl bond against the adjancent C=C bond, gave an angle of 42.0204°, away from (above) the plane. So the cause of the stereoselective attack of the grignard reagent, as the reagent co-ordinates to the oxygen lone pair, in a stabilised chelation arrangement of the intermediate, during the reaction and so directing the methyl group to the same face as the carbonyl group[5]. This is not the most thermodynamically stable expected conformer as a quick calculation of the methyl group on the opposite face to the carbonyl showed a lower energy of 27.3324 kcal/mol compared to 28.8990 kcal/mol for the methyl on the same face as the carbonyl.
For the second reaction studied, inspection the angle of the 3D structure of the reactan (7), gives a dihedral angle of the C=O and C=C of -41.7420°. the stereochemistry of the added group is on the opposite face of the molecule to the carbonyl group. This is due to the directing interference (destabilisation) of the carbonyl lone pairs with the incoming aniline, cf. the chelating stabilisation with a gringard reagent. This causes the attack on the less sterically and stereoelectronically hindered side of the molecule. The actual initial orientation of the carbonyl group is in some part dictated by the adjacent isopropyl group and the steric conformation that it conforms to to minimise the interaction with its adjacent methyl group. The flexing of the adjacent cycloheptane ring, also works to minimise this, along with the interactions with the nitrogen atom.
In order to improve these models, the use of newer force fields which contain metals ions would be helpful. An example is the Merck forcefield, which itself is based on the MM94 forcefield. ChemBio3D also has other limitations. Running the molecule 8, continually gave a flexing of the aromatic π systems, removing the planarity and giving a negative minimised energy for the fnial molecule! An addition to the programming to require aromatic systems to stay planar, would greatly enhance the accuracy of the canculations, it would also decrease the number of local minima.
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
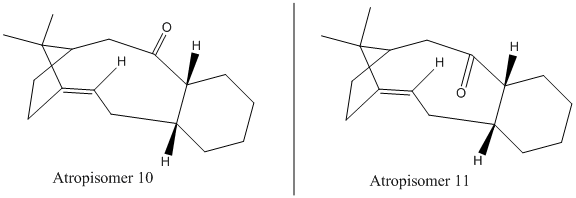
Paquette's total synthesis of Taxol gave the above intermediate in the two atropoisomers. When left to stand, this intermediate isomerises to the alternative carbonyl.[6]. Using the MM2 force field approach again, the two different atropisomers were drawn out and minimised, to investigate which is the more stable. Several attempts to minimise the overall structure resulted in an inversion of the bridgehead (creating another althogether different geometric isomer), as well as the loss of the stereocontrol of the cis double bond, and also of the relative orientation of the hydrogens shared by the cyclohexane cyclodecene ring system (see figure below).
The illustration below shows the incorrect isomer on the left, and the correct isomer on the right, the location of the bridgehead and adjacent carbons having been highlighted in yellow. The hydrogen atoms indicated with green dots should both be above the plane of the ring systems (as is indicated), and the highlighted (yellow) double bond is in the correct cis stereoisomer, not the trans stereoisomer, as was sometimes generated in minimisation.
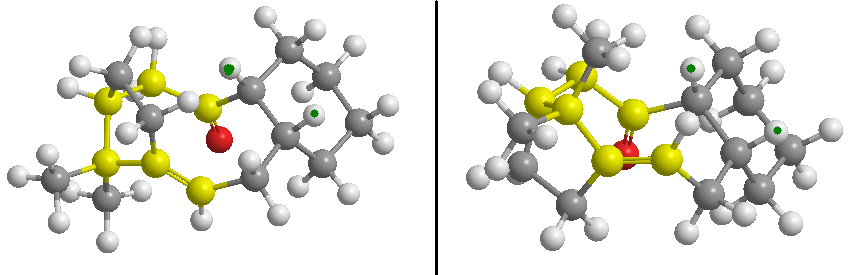
To oversome this obstacle, the molecule was drawn in steps, with sucessive minimisations at each step, in the following order:
- Cyclohexane+cyclodecane ring joined (with stereochemistry of shared hydrogens cis to each other, although it currently does not matter which face of the ring system they are both on).
- Dimethyl bridgehead (on same side of ring system as cis hydrogens in the above step).
- Double bond (with correct cis stereochemistry).
- Carbonyl (with chosen atropisomeric orientation).
After minimising at the final step, several modifications of the molecule were carried out to lower the energy of the molecule. The most fruitful modification was to atropisomer 11, for which the evergy fell from ~48 kcal/mol to the ~44 kcal/mol seen below, by changing the conformation of the cyclohexane component from twist boat to chair.
This resulted in the following molecules with the energies tabled below:
| Contribution Parameter (all in kcal/mol) | Atropisomer (10) | Atropisomer (11) |
|---|---|---|
| Stretch | 2.6775 | 2.5482 |
| Bend | 15.8692 | 10.6201 |
| Stretch-Bend | 0.3963 | 0.3162 |
| Torsion | 18.2527 | 19.7770 |
| Non-1,4 VDW | -1.1341 | -1.3387 |
| 1,4 VDW | 12.6841 | 12.5353 |
| Dipole/Dipole | 0.1451 | -0.1809 |
| Total Energy | 48.8908 | 44.2771 |
From the above, the isomer with the carbonyl pointing downwards (opposite direction to bridgehead carbon) is of lower energy. The force field component that shows the biggest difference is the "bend" component. This component is the strain energy caused by deviation from the optimum bond angle (in this case sp2 120°).
Measurement of the bond angles around the carbonyl carbon gave 115°,118°and 126° for isomer (10) (shown below), and 120° for all three bonds in the isomer (11). NOTE: Values are to 3 s.f.
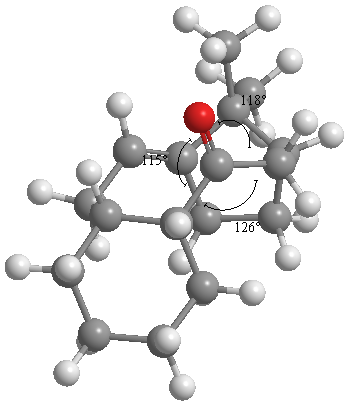
The alkene in the molecule reacts slowly due the relative instability of the corresponding alkane, caused by vicinal and trans-annular strain. The strain energy of an alkene is generally higher than the corresponding alkane (a positive Olefin Strain Energy), however in those with negative OSEs, unsaturation of the bond increases strain, raising the energy of the alkane, as above. This strain in the alkane decreases the ΔHfalkene-ΔHfalkane gap.[7] [8]
How one might induce room temperature hydrolysis of a peptide
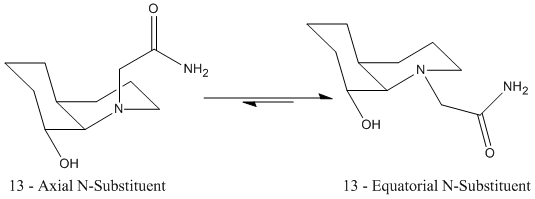
The half life (t1/2) of the hydryolysis of a peptide is approximately 500 years (and netural pH and RT). However by conformational design, this can be encouraged in a much shorter timescale, as in the stereoisomers (13 and 14) shown below :
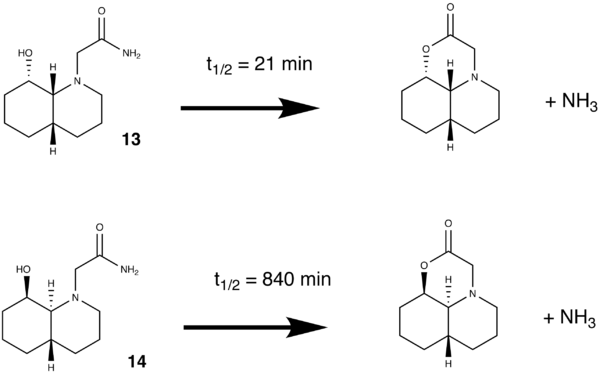
As can be seen, the two stereoisomers show very different reaction rates, and this can be justified by analysing the conformational isomers of each of the stereoisomers shown below:
By minimising and calculating the energies of the isomers using the MM2 force field method, it is possible to rationalise the relative reactivity of each stereoisomer 13 and 14. The JMol models created are shown below:
| 19.2686 kcal/mol | 13.1030 kcal/mol | 11.9533 kcal/mol | 8.9878 kcal/mol |
Starting with stereoisomer 13 which takes the cis-decalin form, inherently contains some unfavourable interactions due to some eclipsed positions (as can be seen throu ha newman projection).For 13 we can also see that the axial conformer is of higher energy as expected due to the presence of a 1,3-diaxial compression interaction (a steric clash), with the adjacent hydrogen.
There are also stabilising hydrogen bonding interactions in both conformational isomers. In the case of the axial N-sub, the amido hydrogen, hydrogen bonds with the oxygen of the equatorial alcohol group. In the equatorial N-sub conformer the amide oxygen hydrogen bonds to the hydrogen of the equatorial alcohol group. The interactions can be seen in the figures, and it should be noted that the O--H-O hydrogen bonding interaction is much stronger and more stabilising than the N-H--O hydrogen bonding interaction (see pauling electronegativities).
In the process of creating the low energy conformers for 13 shown above, various higher energy minima were also seen. This included a double twist boat conformation of the cis-decalin (shown below, left) with an energy of 28.0008 kcal/mol. Another very interesting conformation was also created and minimised in the double twist-boat conformation (below, right) with a extremely high energy of 398.6932 kcal/mol was ao created, with the N-substituent axial, towards the centre of the ring!!! It is clear that this high energy is due to steric clash with the carbons of the cyclohexane ring and the N-sub, and also due to the clash of the amide nitrogen of the N-sub with the hydrogens that it sits in between.
| 28.0008 kcal/mol | 398.6932 kcal/mol |
Stereoisomer 14 takes the trans-decalin form, which is more stable than cis-decalin due to fewer steric interactions, as all hydrogens and subsituents are staggered to those on adjacent carbons. So, it is expected (and seen), that both conformational isomers of 14 that are studied have a lower energy than the conformers of 13. In a similar pattern to stereoisomer 13, the N-sub axial is less stable than the equatorial, due to unfavourable 1,3 diaxial steric interactions (1,3 interaction of the N-sub with the -OH group and hydrogen).
Both the the axial and equatorial conformers of 14 are stabilised further by hydrogen bonding interactions of the axial alcohol group hydrogen, with the oxygen of the amide substituent.
The reactivity of the different isomers
In order for the reaction to occur, the nucleophile oxygen of the alcohol group must be able to attack the electrophilic carbonyl carbon at the optimum stereoelectronic angle of attack. This is known as the Burgi-Dunitz angle [10] of ca. 109°. This angle represents the stereoelectronic interactions of the LUMO of the carbonyl (perpendicular), interacting with the HOMO of the incoming nucleophile. Further direction of the angle of attack is caused by the lone pair of the carbonyl oxygen and its electronegativity interacting with the basic nucelophile. This optimum angle is achieved by the enzymes which would normally catalyse the reaction, lowering the TS energy.
This optimum angle can only be achieved in the above isomers when the alcohol and N-sub are both axial, or both equatorial. So for isomer 13, in which the hydroxyl group is equatorial, the lowest energy conformer is already the more reactive. For isomer 14, the hydroxyl group is axial, and therefore to react intramolecularly, the N-sub must orientate itself axial at energetic cost for the reaction to occur, hence its much larger half life.[11]
The molecules of the reaction of the di-equatorial 13 would give the product on the left, and the diaxial 14, the product on the right:
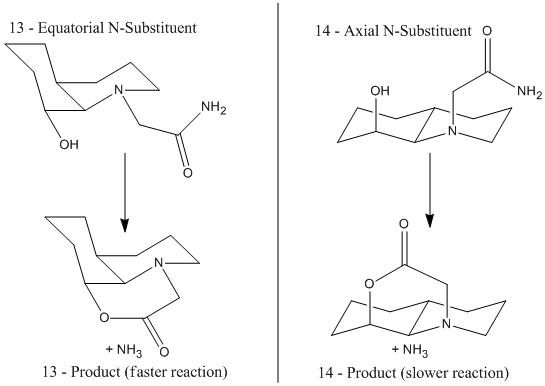
| 28.0008 kcal/mol | 398.6932 kcal/mol |
Modelling Using Semi-empirical Molecular Orbital Theory
After working with simply mechanical molecular modelling approaches, it has become clear that not all reactivity can be explained by classical mechanical approaches. To further explain reactivity and molecular interactions, electronic factors will be investigated to show the influence of the electrons in a molecule need to be considered and how they effect bonds and spectroscopic properties.
Regioselective Addition of Dichlorocarbene
Part 1
Molecule 12 (9-chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene, below) was constructed in ChemBio3D and its optimum geometry calculated using successively more detailed methods:
- MM2 force field (discussed earlier)
- HF/STO-3G self-consistent-field MO method, which gives an approximation of the the valence-electron molecular wavefunction, especially the HOMO, which would generally be the most reactive towards electrophilic attackfive minutes)
- The Density-functional B3LYP/6-31G(d) approach, a more accurate method (see part 2).
The reaction of the molecule with electrophiles (dichlorocarbenes and peracids) shows orbital control. The final method above shows the energy of the orbitals and a graphical representation of their form, taking into account the wave-description of the electrons present.
A jmol representation of the molecules optimised by the three different methods:
Comparing the three methods, we can qualitatively see a change in the shape of the rings. The ring below the chlorine substituent becomes more planar as the optimisation method becomes more advance. This change in geometry is caused by the orbital interactions discussed below. These interactions cause a large change in the reactivity of the molecule on our QM approach in the electrophilic reactions we are concerned with (eg with dichlorocarbene), whereby the attack occurs exclusively at the double bond endo to chlorine (below the chlorine sub).
This is brought about by interaction of the C-Cl antibonding orbital (σ*) with the C=C bonding orbital (π) that is exo to the C-Cl substituent. This removes electron density from the exo double bonding, giving it more single bond character and the donation to σ* orbitals is destabilising to the C-Cl bond, weakening it. We can correlate the strength of the C-Cl bond to the IR spectrum of the compound, since ν (cm-1) is proportional to bond strength.
The above causes two factors that favour the reactivity of the endo double bond[12]:
- Since there is greater electron density in the endo double bond, this is electrostatically more subject to electrophilic attack.
- The stabilising σ*-π interaction would need to be removed for attack to occur on the exo double bond.
The quantum mechanical approach has dealt electronic interactions, giving a more accurate optimisation of the molecules. MM2 ignores the electronic effects, and the HF ignores the electronic correlation term, whereas DFT approximates this as a series of integrals.[13]
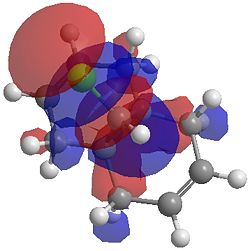
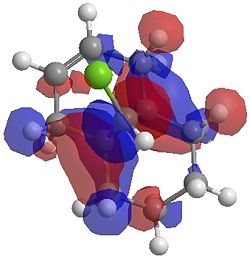
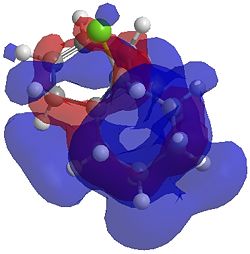
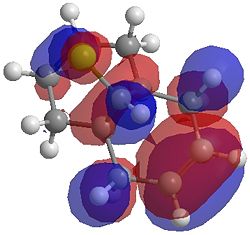
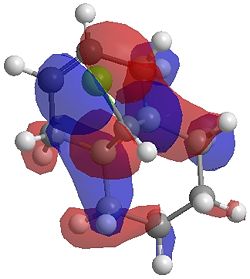
The two optimisation processes above, were repeated for the exo hydrogenated product and the MO surfaces extracted from the checkpoint files of the HF/STO-3G and B3LYP/6-31G(d) moethds. The below shows the LUMO+2, LUMO+1, LUMO, HOMO+1 and HOMO-1 MOs for both the starting molecule 12, and the exo dihydrogenated product.
| Orbital | Molecule 13 | Molecule 13 | Molecule 13 Hydrogenated | Molecule 13 Hydrogenated |
|---|---|---|---|---|
| LUMO+2 | HF/STO-3G (D-space: http://hdl.handle.net/10042/to-1673) | B3LYP/6-31G(d) (D-space: http://hdl.handle.net/10042/to-1675) | HF/STO-3G (D-space: http://hdl.handle.net/10042/to-1702) | B3LYP/6-31G(d)(D-space: http://hdl.handle.net/10042/to-1703) |
| LUMO+2 | 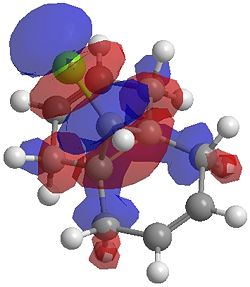 |
 |
 |
 |
| LUMO+1 | 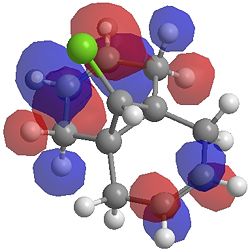 |
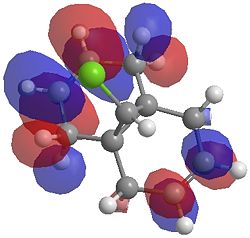 |
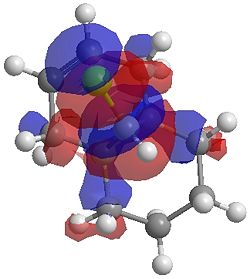 |
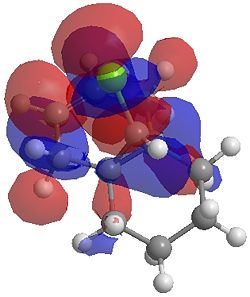 |
| LUMO | 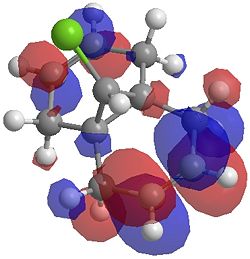 |
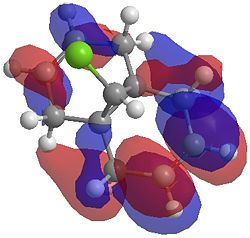 |
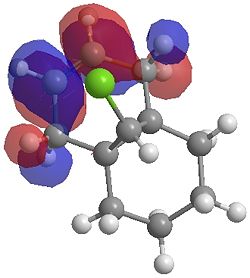 |
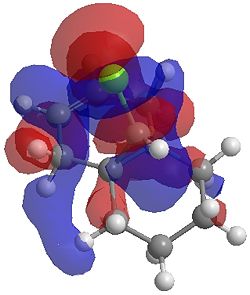 |
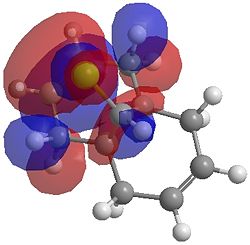
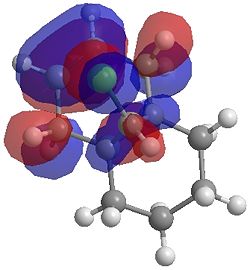
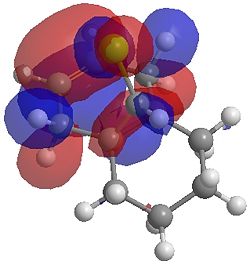
| HOMO | 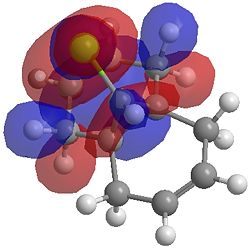 |
 |
 |
 |
| HOMO-1 | 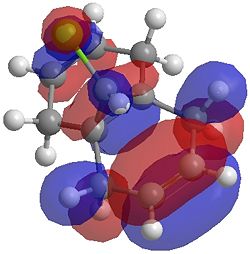 |
 |
 |
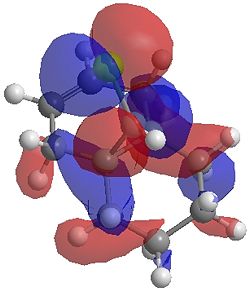 |
One of the first thing we notice upon viewing the MO surfaces in ChemBio3D is that far more molecular orbitals have been calculated by the B3LYP/6-31G(d) method. Another diffence is the vast amount of electron density added in the LUMO orbitals of the hydrogenated product by the more advanced calculation. A comment we would make is no appreciable overlap of the σ* to π is seen in these diagrams. However the literatures shows as having been run at a lower level of theory (PM3), so it would seem that lower levels of theory are more suitable for analysis of the molecular orbitals (as per literature). However the higher levels utilised by us are more suited to calculated bond lengths, force constants, IRs etc.
Part 2
|
As predicted in the above section, the donation of π electron density to the σ* orbital has caused a weakening of the exo π bond, as accounted for by the decrease in stretching frequency to ~1740cm-1 cf. ~1760cm-1. The bond length of the exo bond in 13 is therefore lengthened (greater s character) to 1.33570Å cf. 1.33214Å for the endo. |
Organic Computational Chemistry - Part 2 - Structure based Mini project using DFT-based Molecular orbital methods
Assigning Regioisomers in Click Chemistry
The philosophy of click chemistry is one that was introduced by K. Barry Sharpless (a review by Sharpless et al.[14]), one of the discoverers of the Cu(I) based catalysation of the Azide Alkyne Huisgen cycloaddition, a 1,3-dipolar cycloaddition. The speed and ease of this Cu(I) catalysed cycloaddition, has made it one of the most well known examples of this philosophy and his been described by Sharpless as the "cream of the crop" of click chemistry reactions.
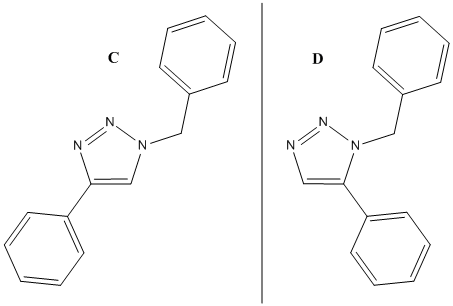
The substituted product we shall analyse are shown on the right hand side and are taken from lit.
[15]
It is possible to differentiate between the two isomers using 13C NMR, and so each molecule was optimised using the MM2 method, and then a mpw1pw91 optimisation using the 6-31G(d,p) basis set. This was followed by an NMR prediction calculation, the values for which were compared to the literature.
Isomer C: 1,4-Product
Below the literature NMR [16] was compared to the calculated NMR. (1,4 Optimisation D-Space: http://hdl.handle.net/10042/to-1704)(1,4 NMR D-Space: http://hdl.handle.net/10042/to-1692).
The analysis shown below is the variance formula:
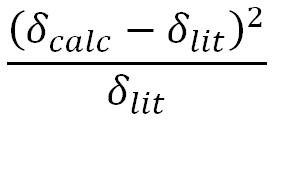
Since variances are additive, the sum of the variances is shown at the bottom of the column. Variance shows the degree by which the data achieved experimentally is different from our calculated data.
NOTE: The literature data has been treated as the population mean, and the calculated data as our sample. Hence the literature is treated as correct.
| Calculated Chemical Shift/ppm | Lit. Chem Shift/ppm | Variance |
|---|---|---|
| 54.65 | 54.00 | 0.0078 |
| 117.25 | 119.50 | 0.0424 |
| 121.32 | ||
| 121.90 | ||
| 124.21 | ||
| 124.39 | ||
| 124.49 | ||
| 124.87 | 125.50 | 0.0032 |
| 124.94 | 127.90 | 0.0684 |
| 125.06 | 128.56 | 0.0954 |
| 125.26 | 128.64 | 0.0888 |
| 125.57 | 128.90 | 0.0858 |
| 127.43 | 130.40 | 0.0675 |
| 133.02 | 134.60 | 0.0186 |
| 145.06 | 148.00 | 0.0586 |
| 0.5365 |
Isomer D: 1,5-Product
(1,5 Optimisation D-Space: http://hdl.handle.net/10042/to-1705) (1,5 NMR D-Space: http://hdl.handle.net/10042/to-1693)
| Calculated Chemical Shift/ppm | Lit. Chem Shift/ppm | Variance |
|---|---|---|
| 52.49 | 51.85 | 0.0080 |
| 124.14 | ||
| 124.49 | ||
| 124.80 | ||
| 124.82 | ||
| 124.99 | 126.93 | 0.0297 |
| 125.08 | 127.22 | 0.0360 |
| 125.22 | 128.22 | 0.0704 |
| 125.33 | 128.92 | 0.1001 |
| 125.49 | 129.08 | 0.0998 |
| 125.97 | 129.64 | 0.1041 |
| 126.68 | 133.26 | 0.3251 |
| 130.22 | 133.34 | 0.0729 |
| 131.61 | 135.66 | 0.1211 |
| 136.54 | 138.26 | 0.0214 |
| 0.9886 |
NMR Comparison of the two Isomers
Looking at the molecules, the position of the R1 and R2 affects the location of the -CH2 carbon. In the 1,4 product it is in the 5 position and in the 1,5 product the 4 position. At the 5 position, between two aromatic Ph rings, the -CH2 carbon is more deshielded (1,4 product calculated is 145.06ppm and 148.0ppm lit. compared to 1,5 product, 136.54ppm calculated and 138.26ppm lit.
Closing Comments
By simple qualitative observation, and by applying mathematical techniques (variance analysis), it is clear that the 13C NMR calculated are a very good match to the literature values given/obtained. However it should be noted, that for some calculated values no matching literature value was available, and for these values no vairance is given. It should also be noted that the literature values are matched to the calculated values wwith some ambiguity. For example, the 126.93ppm is matched for 124.99ppm for the 1,5product, but could actually be the assignment for the 124.82, because the two calculated values are so marginally different. The reason for these large nunmber of peaks is that Gaussian is able to "perfectly" give chemical shifts to all carbons. However NMR machines have a set resolution, so when two peaks become extremely close together, they merge with an integral the sum of the two constituent peak integrals. This is advantageous as we can discern, using the calculated NMR as a tool, the peaks that may have merged to give out experimental peaks.
A disadvantage of the computational method is that it does not show coupling and splitting of the peaks, for example the 1:1:1 peak split on the -CH by the nitrogen.
References
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Mod:organic
- ↑ 2.0 2.1 https://www.ch.ic.ac.uk/wiki/index.php/Mod:molecular_mechanics
- ↑ http://en.wikibooks.org/wiki/Computational_chemistry/Molecular_mechanics
- ↑ U. Burkert and N. L. Allinger, Molecular Mechanics, ACS Monograph 177, (ACS,Washington,1982)
- ↑ A. G. Shultz, L. Flood and J. P. Springer, J. Org. Chemistry, 1986, 51, 838. DOI:10.1021/jo00356a016
- ↑ S. W. Elmore and L. Paquette, Tetrahedron Letters, 1991, 319; DOI:10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0
- ↑ Pelayo Camps, Francesc Pérez, Santiago Vázquez, Tetrahedron, Volume 53, Issue 28, 14 July 1997, Pages 9727-9734; DOI:10.1016/S0040-4020(97)00595-4
- ↑ PWilhelm F. Maier, Paul Von Rague Schleyer, TJournal of the American Chemical Society 1981 103 (8), 1891-1900 ; DOI:10.1021/ja00398a003
- ↑ Prof. H. Rzepa, Mod:Organic - - Wiki [1] (accessed 01/02/2009)
- ↑ H. B. B:urgi, J. D. Dunitz, J. M. Lehn and G. Wipff, Tetrahedron, Volume 30, Issue 12, 1974, Pages 1563-1572 . DOI:10.1016/S0040-4020(01)90678-7
- ↑ M. Fernandes, F. Fache, M. Rosen, P.-L. Nguyen, and D. E. Hansen, 'Rapid Cleavage of Unactivated, Unstrained Amide Bonds at Neutral pH', J. Org. Chem., 2008, 73, 6413–6416 ASAP: DOI:10.1021/jo800706y
- ↑ B. Halton, R. Boese and H. S. Rzepa., J. Chem. Soc., Perkin Trans 2, 1992, 447. DOI:10.1039/P29920000447
- ↑ Jack Paget, Gaussian, [2], (accessed 05/02/2008)
- ↑ Hartmuth C. Kolb, M. G. Finn, K. Barry Sharpless, Angewandte Chemie International Edition, 2001, 40, 11, 2004-1011; DOI:<2004::AID-ANIE2004>3.0.CO;2-5 10.1002/1521-3773(20010601)40:11<2004::AID-ANIE2004>3.0.CO;2-5
- ↑ Li Zhang,† Xinguo Chen,† Peng Xue,† Herman H. Y. Sun,† Ian D. Williams,† K. Barry Sharpless,‡ Valery V. Fokin,*‡ and Guochen Jia*†;, J. Am. Chem. Soc., 2005, 127 (46), pp 15998–15999; DOI:10.1021/ja054114s
- ↑ Ionic Polymer Supported Copper(I): A Reusable Catalyst for Huisgen's 1,3-Dipolar Cycloaddition, Uthaiwan Sirion, Yu Jin Bae, Byoung Se Lee, Dae Yoon Chi, Synlett 2008 2326-2330 DOI:10.1055/s-2008-1078245