Rep:Mod:wkg15ts

Introduction

Computation methods are widely employed nowadays to numerically solve the Schrödinger Equation of complex molecules to understand them at an ab initio level. Gaussian is one such computational tool, along with Gaussview to assist visualisation of the species under investigation.
Various computation methods can be applied to reach the goal, with different degrees of accuracy and required computational resources. In this experiment, semi-empirical method PM6 and a more accurate Density Functional Theory (DFT) method B3LYP were used. PM6 takes into account empirical data to generate results, and so is quicker and lighter. B3LYP relies more on ab initio calculations and is based on Hartree-Fock method. It is generally advised to use PM6 to generate initial results, then use higher methods for cleaner optimisation.

Nf710 (talk) 22:57, 28 November 2017 (UTC) B3LYP is a DFT based method that uses HF to correct the exchange corelation problem

In the experiment, Diels-Alder reaction, inverse electron demand Diels-Alder Reaction, and the competition between Diels-Alder and cheletropic reactions were studied, by optimising transition structures, simulating reaction pathways by Intrinsic Reaction Coordinate (IRC) calculations, and comparing energies and MO structures.

Potential energy surface is a profile that shows the energy of the species in a system. The z-coordinate is the energy while the x- and y- axes are usually the coordinates of the atoms involved (if the system is small). However, normal modes have to be used as the x- and y- axes instead when the system is larger. A system has (3N-6) normal modes, where N= number of atoms, which are all orthogonal to each other. Gaussian chooses the 2 most suitable normal modes and creates a PES. A chemical reaction travels along the lowest energy pathway connecting reactants and products, and the goal of most simulations in this experiment is to look for this pathway.

Nf710 (talk) 23:05, 28 November 2017 (UTC)Gaussian calucates with all 3N-6 normal modes at the same time

A minimum in a PES corresponds to a structure with a local minimum in energy. At this point the gradient, i.e. the first derivative of the curve, will be zero, meaning the system is at a local equilibrium. The second derivative is positive at this point, since the curve will be increasing for any movement away from this point.

Nf710 (talk) 23:05, 28 November 2017 (UTC) curvature is positive in all 3N-6 directions

A transition state is a point of local maximum along the aforementioned lowest energy reaction pathway on the PES. At this point, the first derivative is also zero since its curvature is zero, but its second derivative will be negative, corresponding to a decrease in any displacement away from this point.

23:07, 28 November 2017 (UTC) At a TS all the Normal modes have positive curavture, apart from 1 which is the reaction coordinate

Frequency calculation applies simple harmonic motion equations at a specific point of the structure. The second derivative of the PES is taken as the force constant in the equation, taken with a square root. It is for this reason that we can find an unique vibrational mode with a negative frequency only for a TS structure. (Gaussian represents imaginary vibrations as negative.)

Exercise 1: Reaction of Butadiene with Ethylene

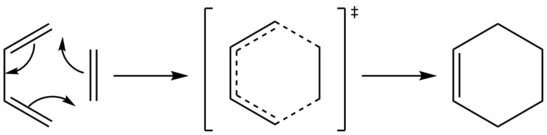
Reaction between butadiene and ethylene is a good demonstration of pericyclic [4+2] Diels-Alder reaction. Reactants, products and transition states were optimised at the PM6 level for MO study of this simple Diels-Alder reaction. Frequency calculation and IRC were run to illustrate the reaction mechanism and confirm the transition state structure.

Transition state and mechanism

The optimised structure showed only one negative frequency at -949.13 cm^-1 in Fig. 2, corresponding to a synchronous C-C bond formation. This shows that the Diels-Alder reaction between butadiene and ethylene is a concerted process, further shown with an IRC result in Fig. 3. IRC with RMS gradient can be found here.

	Fig. 3: reaction pathway from IRC calculation
Fig. 2: vibrational frequency of the transition state	Fig. 3: reaction pathway from IRC calculation

Bond Length Comparison

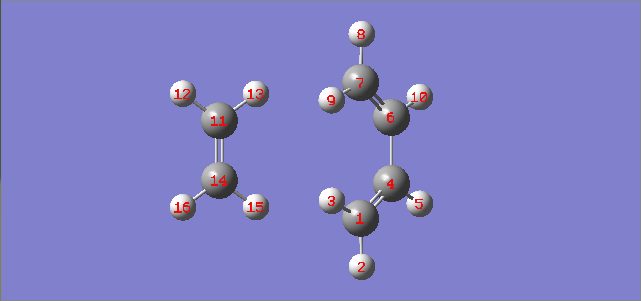
Fig. 4: labels for carbons
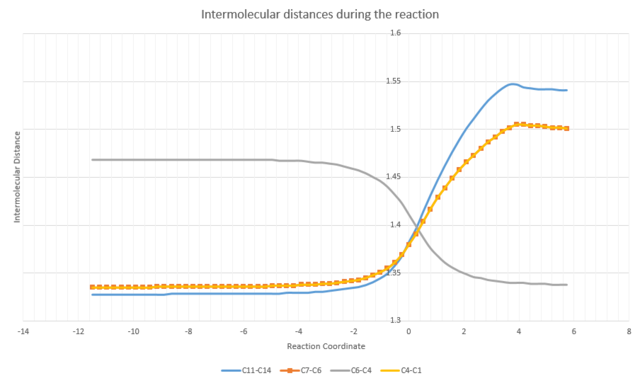
Fig. 4: labels for carbons	Fig. 5: Variation of bond distances during reaction

The change in bond lengths can be followed with IRC calculations, giving insights into the type of bonds formed or broken during the reaction:

C11-C14 (of the ethene) increased from 1.33Å to 1.54Å, indicating a change from sp²tosp³hybridisation.

C7-C6 and C4-C1 (vinyl parts of butadiene) increased from 1.34Å to 1.50Å, indicating a change from sp²tosp³hybridisation.

C6-C4 (alkyl part of butadiene) decreased from 1.47Å to 1.34Å, indicating a change from sp³tosp²hybridisation.

At the transition state, all 4 aforementioned bonds value between C-C and C=C bond lengths, showing the transition between their initial and final bond types.

As for C11-C7 and C14-C1, at the transition state, since C-C bonds were forming, their distances(2.12Å) were smaller than twice of the Van der Waals radius(1.7Å) of the C atom. (Fv611 (talk) True, but how do they compare to the sp3 single bond distances?)

Further work can be done on looking at the bond angles as a second confirmation on the carbons' hybridisation.

Table 1: C-C bond lengths(Å) at various states
	C11-C14	C7-C6	C6-C4	C4-C1	C11-C7	C14-C1
Reactants	1.327	1.335	1.468	1.335	3.414^*	3.414^*
TS	1.382	1.38	1.411	1.38	2.115	2.115
Product	1.541	1.501	1.338	1.501	1.54	1.54

^*: reactants would be assumed to be at infinite separation at an ideal situation.

Molecular Orbital Analysis

A proposed MO diagram for the formation of TS for the reaction is shown in Fig. 6.

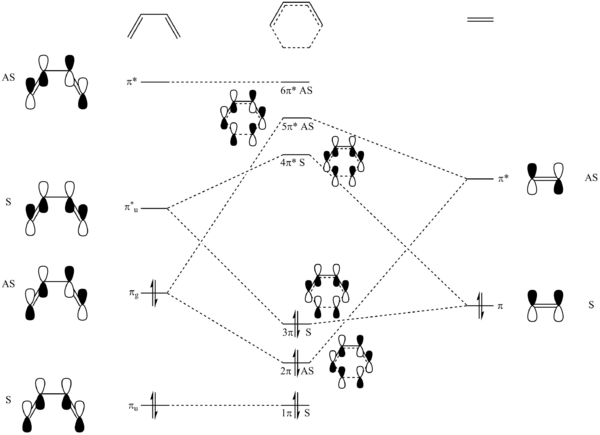
The HOMO and LUMO of butadiene and ethene, and the four MOs they produce for the TS are presented here (to save loading time), and compared with the proposed MOs in the above MO diagram.

(Fv611 (talk) The MO diagram is correct in the pairings that you have selected, but from the MOs you have calculated, you know that the energies of both the butadiene HOMO and the ethene HOMO are lower than that of the TS HOMO-1, so why not draw them that way? Similarly, you know from your calculated MOs that the energy of the ethene LUMO is higher than the LUMO+1.)

MO theory requires the MOs to have the same symmetry (both symmetric or both anti-symmetric) in order to react successfully and form new MOs, otherwise the orbital overlap integral is zero and thus a "forbidden" reaction. This is supported positively in this experiment that the TS frontier MOs (FMO)^[1] are constructed by mixing orbitals of the same symmetry (AS-AS or S-S) from the reactants. In this case, the symmetric MOs are responsible for the formation of both the HOMO and LUMO in the TS.

Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

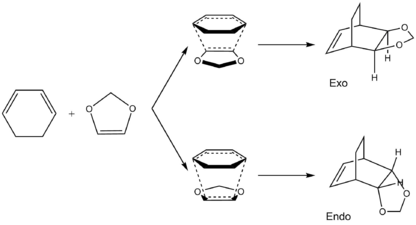
Reaction between cyclohexadiene and 1,3-dioxole can be used to demonstration of an inverse electron-demand Diels-Alder reaction.

Molecular Orbital Analysis

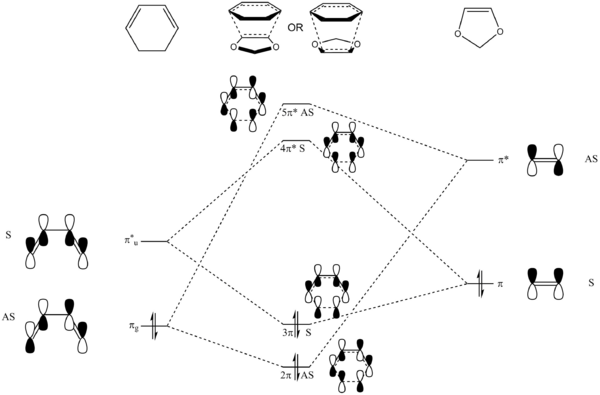
MOs of the optimised TS are displayed here. It can once again be seen that only MOs of the same symmetry can interact.

(Fv611 (talk) Your MOs are calculated correctly, but the diagram is not representative of their relative energies. The TS MOs have a higher energies than the diene HOMO, and the dienophile LUMO has the highest energy. This is what makes it an inverse demand Diels-Alder, not only the type of substituents as you mention later.)

For this molecule pair, the TS HOMO and LUMO are symmetric, the same as that in Exercise 1.

However, in Exercise 1, the TS HOMO/LUMO pair is formed by mixing butadiene LUMO and ethene HOMO, whereas in this Exercise, it is due to the mixing of cyclohexadiene LUMO and 1,3-dioxole HOMO. This demonstrates the inverse electron-demand Diels-Alder reaction, as the dienophile is electron-rich while the diene is electron-poor. This can be explained by the presence of electron-donating O on the 1,3-dioxole, thus raising the energy of its HOMO.

Energetics Analysis

The Gibbs free energy of reactants, transition states and products at room temperature are extracted from their respective optimisation .log files under the "Sum of electronic and thermal Free Energies" section (Table 2). This allows for the calculation of reaction energies and barriers.

Table 2: Gibbs Free Energies of reactants, transition states and products at 298K, and energetics of the reactions
	Gibbs Free Energies										Reaction Energy		Activation Energy
	1,3-dioxole		Cyclohecadiene		Reactants at infinite separation		Transition State		Product		Reaction Energy		Activation Energy
	Hartrees	kJ/mol	Hartrees	kJ/mol	Hartrees	kJ/mol	Hartrees	kJ/mol	Hartrees	kJ/mol	Hartrees	kJ/mol	Hartrees	kJ/mol
endo	-267.068132	-701187.43398	-233.321033	-612584.418806	-500.389165	-1313771.853	-500.332154	-1313622.17039	-500.418695	-1313849.38381	-0.02953	-77.53102	0.057011	149.6824
exo	-267.068132	-701187.43398	-233.321033	-612584.418806	-500.389165	-1313771.853	-500.329164	-1313614.32015	-500.41732	-1313845.7737	-0.028155	-73.92091	0.060001	157.53264

The endo-product has both a lower activation barrier and a more negative reaction energy, meaning it is both kinetically and thermally more favorable. The reason for the more kinetic pathway of the endo-product is the existence of secondary orbital interaction between the oxygen p-orbital and sp²-orbitals of the diene carbons, as illustrated in Fig. 9. As for the more thermal result, in normal circumstances, the exo-compound is expected to be more thermally favored. However, it is shown otherwise for this reaction. One possible explanation can be considering the steric clash between the terminal H in the dioxole and the H in the bridging ring, thus destabilising the exo-product.

Nf710 (talk) 23:16, 28 November 2017 (UTC) This was a nice consise secioon, Y9ur energies look slightly out. Your drawing of the SOO is really instructive and your arguments for inverse demand and th kentic product are good

Exercise 3: Diels-Alder vs Cheletropic

O-xylylene-sulphur dioxide cycloaddition was studied in this exercise. The reactants can perform Diels-Alder or cheletropic reaction, and since O-xylene has two sites of cis-diene (internal and external), both reactions can perform at the two sites, thus giving 6 total possible reactions shown in Table 3. Each of the 6 reactions was optimised and simulated with PM6 method, visualised with IRC calculation. Thermochemical information was extracted to determine which route is preferred.

Table 3: Reaction Schemes and Pathways of the 6 Reactions
Diene location	Reaction type
Terminal	Diels-Alder	Endo
	Diels-Alder	Exo
	Cheletropic
Internal	Diels-Alder	Endo
	Diels-Alder	Exo
	Cheletropic

IRC energy and gradients can be found here.

Energetics Analysis

The Gibbs free energy of reactants, transition states and products at room temperature are extracted from their respective optimisation .log files under the "Sum of electronic and thermal Free Energies" section (Table 4). This allows for the comparison of activation barriers and reaction energies, and the creation of a reaction profile to visualise the differences.

Table 4: Gibbs Free Energies of reactants, transition states and products at 298K, and energetics of the reactions
	Reaction Type		Gibbs Free Energies										Reaction Energy	Activation Energy
			Sulfur Dioxide		O-xylylene		Reactants at infinite separation		Transition State		Product		Reaction Energy	Activation Energy
			Hartrees	kJ/mol	Hartrees	kJ/mol	Hartrees	kJ/mol	Hartrees	kJ/mol	Hartrees	kJ/mol	kJ/mol	kJ/mol
Terminal	Diels-Alder	endo	-0.118614	-311.4210807	0.178292	468.105682	0.059678	156.6846013	0.090563	237.773175	0.021697	56.9654778	-99.7191235	81.0885737
	Diels-Alder	exo							0.092076	241.745556	0.021454	56.3274813	-100.35712	85.0609547
	Cheletropic								0.099061	260.084675	0.000001	0.0026255	-156.6819758	103.4000737
Internal	Diels-Alder	endo							0.10207	267.98481	0.065609	172.256443	15.5718417	111.3002087
	Diels-Alder	exo							0.105054	275.819298	0.067307	176.714542	20.0299407	119.1346967
	Cheletropic								0.113006	296.697276	0.077424	203.276727	46.5921257	140.0126747

Terminal dienes react to give exothermic products while the internal fragment gives endothermic reactions. This is largely due to the stabilisation of terminal products from the formation of a benzene fragment. The internal reaction also has a higher activation barrier, due to the fact that the reactants have to come at a hindered position, and more rearrangements in the structure are required.

Within terminal products, cheletropic reaction is more thermally favored (more negative reaction energy), for it has formed 2 strong C-S bonds and not broken S-O bond. Diels-Alder reaction is more kinetically favored (smaller activation energy), with the endo-product once again more favored kinetically due to secondary orbital interaction, similar to the one shown in Exercise 2. The endo-rule also applies to the reaction in the internal fragment.

It can be seen that the internal cheletropic reaction is the most unfavoured reaction both kinetically and thermally.

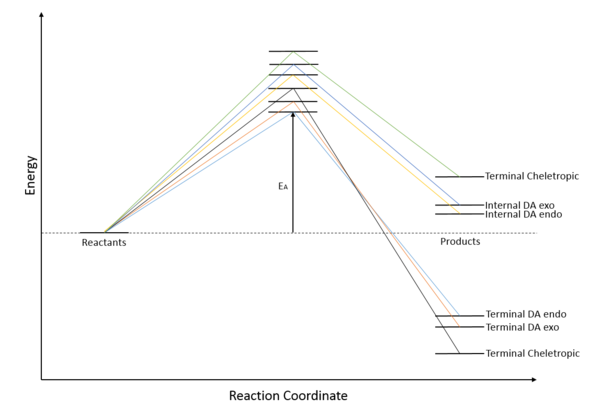
(You could provide some discussion about the results you've got Tam10 (talk) 10:33, 24 November 2017 (UTC))

Conclusion

Computational methods were employed to investigate 3 situations of Diels-Alder reactions. In Exercise 1, a typical pericyclic [4+2] Diels-Alder reaction was demonstrated by a reaction between butadiene and ethene. In Exercise 2, reaction between cyclohexadiene and 1,3-dioxole was used to demonstrate an inverse electron-demand Diels-Alder reaction. In Exercise 3, O-xylylene-sulphur dioxide cycloaddition was studies to compare the energetics of Diels-Alder and cheletropic reactions.

Various effects that affect kinetics or thermodynamics, such as secondary orbital interaction, were postulated to explain the preference of the products formed.

Reactants, products and transition states were optimised with either semi-empirical PM6 or DFT B3LYP methods, with IRC calculations carried out with respective methods.

Reference

[1]: Ian Fleming, Frontier Orbitals and Organic Chemical Reactions, Wiley, London, 1976