Rep:Mod:winger15
Inorganic Computational lab: Mod 2
Introduction
In this module, Gaussian was used to model molecules. It was used in the optimisation, IR analysis among other things to yield very reliable and accurate results in terms of bond length, angles and many other phyiscal properties. Due to this very accurate resultsand the fact that no potentially dangerous, expensive reactions need to be done, these calculations are often preferred compared to carrying out experiments.
For the various exercises in this module, different basis sets were made in order to get an accurate depiction of the many diverse molecular orbitals. It is important to get a balance on the number and type of basis sets since a very accurate basis set may be accurate but it would take a long time while a lack of accuracy would occur if a very basic basis set was used.
Density Functional Theory (DFT)is the sole approximation method that is used in the module. This is used with a B3LYP functional and this is far more accurate than Hartree-Fock method and Molecular Mechanics methods.
BH3
The optimisation of BH3:

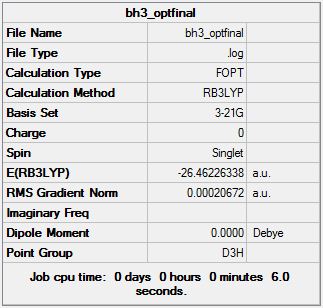
The molecule of BH3 was drawn on GaussView with the each B-H bond being extended to 1.5 Angstroms. After this an optimisation calculation was done on the BH3 molecule, where a 3-21g basis set with a B3LYP method was used. The Jmol of the optimised structure can be seen through the link above. The main details from the optimisation can be seen in the summary on the right and the full details can be seen here DOI:10042/to-13224 .
The section below, cut from the logfile above, shows that the reaction has indeed converged and proves that the calculation has finished. The iterations were done until a gradient of 0 was reached, as seen in the derivative info.
Item Value Threshold Converged?
Maximum Force 0.000413 0.000450 YES
RMS Force 0.000271 0.000300 YES
Maximum Displacement 0.001610 0.001800 YES
RMS Displacement 0.001054 0.001200 YES
Predicted change in Energy=-1.071764D-06
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1935 -DE/DX = 0.0004 !
! R2 R(1,3) 1.1935 -DE/DX = 0.0004 !
! R3 R(1,4) 1.1935 -DE/DX = 0.0004 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The optimisation of the molecule is shown below. The optimisation procedure occured via 3 iterations. From these pictures we can see that during the 1st and 2nd optimisation that no B-H bonds are formed suggesting that the distance is too great, however this is due the limit that Gaussview specifies as a bond. Thus bonds are not displayed.
 |
 |
 |
 |
|---|


Natural population analysis

From the Natural Bond Order Analysis we can see distribution of electron density within this BH3 molecule We can observe that there is a lack of electron density around the boron atom, while some electron density is seen in each of the hydrogen atoms. It show that hydrogen is more electronegative than boron and shows why boron is a very effective Lewis acid with its electron deficient boron center.
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
B 1 0.19785 1.99962 2.80253 0.00000 4.80215
H 2 -0.06595 0.00000 1.06582 0.00013 1.06595
H 3 -0.06595 0.00000 1.06582 0.00013 1.06595
H 4 -0.06595 0.00000 1.06582 0.00013 1.06595
=======================================================================
* Total * 0.00000 1.99962 5.99998 0.00040 8.00000
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.98096) BD ( 1) B 1 - H 2
( 46.65%) 0.6830* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.0000 0.0000
0.8165 0.0000 0.0000 0.0000
( 53.35%) 0.7304* H 2 s(100.00%)
1.0000 0.0005
2. (1.98096) BD ( 1) B 1 - H 3
( 46.65%) 0.6830* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 -0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 53.35%) 0.7304* H 3 s(100.00%)
1.0000 0.0005
3. (1.98096) BD ( 1) B 1 - H 4
( 46.65%) 0.6830* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 53.35%) 0.7304* H 4 s(100.00%)
1.0000 0.0005
4. (1.99962) CR ( 1) B 1 s(100.00%)
1.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000
5. (0.00000) LP*( 1) B 1 s(100.00%)
6. (0.00000) RY*( 1) B 1 s( 0.00%)p 1.00(100.00%)
7. (0.00000) RY*( 2) B 1 s( 0.00%)p 1.00(100.00%)
8. (0.00000) RY*( 3) B 1 s( 0.00%)p 1.00(100.00%)
9. (0.00000) RY*( 4) B 1 s( 0.00%)p 1.00(100.00%)
10. (0.00013) RY*( 1) H 2 s(100.00%)
-0.0005 1.0000
11. (0.00013) RY*( 1) H 3 s(100.00%)
-0.0005 1.0000
12. (0.00013) RY*( 1) H 4 s(100.00%)
-0.0005 1.0000
13. (0.01903) BD*( 1) B 1 - H 2
( 53.35%) 0.7304* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.0000 0.0000
0.8165 0.0000 0.0000 0.0000
( 46.65%) -0.6830* H 2 s(100.00%)
1.0000 0.0005
14. (0.01903) BD*( 1) B 1 - H 3
( 53.35%) 0.7304* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 -0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 46.65%) -0.6830* H 3 s(100.00%)
1.0000 0.0005
15. (0.01903) BD*( 1) B 1 - H 4
( 53.35%) 0.7304* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 46.65%) -0.6830* H 4 s(100.00%)
1.0000 0.0005
A stationary point had been reached but it is not possible to know if a minimum has been reached and even if a minimum has been reached whether the right minimum has been reached. If the correct minimum was truly reached then any movement of atoms in the molecule should result in an increase in the overall energy of the molecule. A maximimum would mean the molecule would lose energy if the shape of the molecule is altered. Any vibrational frequencies would have to be only positive for the stationary point to be a minimum.
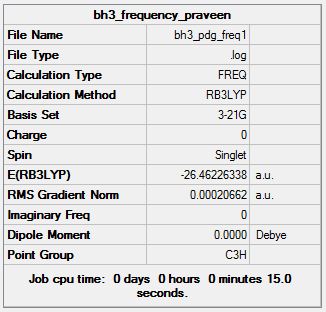
IR analysis of BH3
A Vibrational calculation was done to obtain the different vibrational modes shown by the BH3 molecule. As can be seen in the summary below an RB3LYP calculation method was done with a 3-21G basis set. The calculation type was set to frequency. Since all the frequencies were positive, we can be sure a successful optimisation has occurred. The full file can be obtained from this link. https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:BH3_PDG_FREQ1.LOG
| Full IR spectrum | Frequency | Intensity | Description | Symmetry |
|---|---|---|---|---|
| Mode 1 | 1144cm-1 | 93 | Wagging - B-H bonds bend in-phase, in and out of the plane. Large dipole moments occur as a consequence of this. | A2 |
| Mode 2 | 1204cm-1 | 12 | Scissoring - While one B-H bond remains static, the other two bonds bend towards and then away from each other. | E' |
| Mode 3 | 1204cm-1 | 12 | Rocking - Two B-H bonds bend in the same direction (anti-clockwise) while the other B-H bond bends clockwise. | E' |
| Mode 4 | 2598cm-1 | 0 | Symmetric stretch - All three B-H bonds bend in sync with each other, lengthening and then shortening the bond. Symmetry is preserved and there are no dipole moment changes meaning this is an IR inactive stretch. | A1 ' |
| Mode 5 | 2737cm-1 | 104 | Asymmetric stretch - One B-H bond remains still, while the other two stretch π radians out of phase. | E' |
| Mode 6 | 2737cm-1 | 104 | Asymmetric stretch - Two B-H bonds are stretching in phase with each other while the other B-H bond is again π radians out of phase. This leads to a large dipole moment change hence a large peak. | E' |
Three peaks are only observed. This is because one of the peaks cannot be observed since it does not cause a change in dipole. Moreover there a two sets of two peaks that are degenerate leading to 3 intense signals.
MO Analysis
As in previous calculations a B3LYP method with 6-31g basis set was used with a full NBO. The MOs obtained from this molecule were illustrated on an MO diagram below.


TlBr3
Optimisation
Like the optimisation of BH3, the optimisation of TlBr3 involved using a DFT and B3LYP method, the difference in the two optimisations came in the use of LanL2DZ basis set. By using this more accurate basis set, it was ensured that electrons on the thallium atom were not being neglected and thus accurate modelling of the TlBr3 molecule was possible.the optimised structure can be viewed in the Jmol link above. The summary of this optimisation is shown below. Further to this the opint group of the molecle was restricted to D3H and the tolerance of this calculation was restricted to very tight to obtain the most accurate calculation possible.




 |
 |
 |
|---|
The bond length of the Tl-Br bond is 2.65 Angstroms according to the calculation while the bond angle is 120 degrees. The literature value of 2.512 Angstroms[2]. supports that idea that the calculation is fairly accurate while the bond angle suggests that the bond angle is indeed 120 degrees
Item Value Threshold Converged?
Maximum Force 0.000002 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000022 0.001800 YES
RMS Displacement 0.000014 0.001200 YES
Predicted change in Energy=-6.082801D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 2.651 -DE/DX = 0.0 !
! R2 R(1,3) 2.651 -DE/DX = 0.0 !
! R3 R(1,4) 2.651 -DE/DX = 0.0 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
IR Analysis
The calculation for obtaining the vibrational frequencies was done using the method and the basis set shown below. All information regarding this calculation i available in the adjacent link. https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:TLBR3_FREQ_PDG.LOG

| Full IR spectrum | Frequency | Intensity | Description | Symmetry |
|---|---|---|---|---|
| Mode 1 | 46cm-1 | 4 | Scissoring - Two Tl-Br bonds bend towards each other, while one TlBr bond remains the same. Large dipole moments occur as a consequence of this. | A2" |
| Mode 2 | 46cm-1 | 4 | Rocking - Two B-H bonds bend in the same direction (anti-clockwise) while the other B-H bond bends clockwise | E' |
| Mode 3 | 52cm-1 | 6 | E' | |
| Mode 4 | 165cm-1 | 0 | Wagging - Tl-Br3 bonds bend in-phase, in and out of the plane. Large dipole moments occur as a consequence of this. | A1 ' |
| Mode 5 | 211cm-1 | 35 | Asymmetric stretch - One Tl-Br bond remains still, while the other two stretch π radians out of phase. | E' |
| Mode 6 | 211cm-1 | 25 | Asymmetric stretch - Two Tl-Br bonds are stretching in phase with each other while the other Tl-Br bond is again π radians out of phase. This leads to a large dipole moment change hence a large peak. The cause | E' |
Low frequencies --- -3.4213 -0.0026 -0.0004 0.0015 3.9367 3.9367
Low frequencies --- 46.4289 46.4292 52.1449
Even though there are some negative frequencies which implies that the true minimum has not been found, the magnitude of these frequencies are small and therefore acceptable. The explanation for the three peaks is very similar to that of the BH3 molecule where there is one IR inactive stretch causing no peak and then two doubly degenerate peaks forming the three peaks.
What is a bond?
A bond can only be defined if the electron density within molecular orbitals is analysed. There are three main types of bonding. The first eing covalent bonding which involves the sharing of pair(s) of electrons between and two atoms, usually to form stable octet electron shells. Ionic bonding is caused by two ions of the opposite charge interacting strongly. the thrid type is metalic bonding where a "sea" of delocalised electrons is moing round a core of metal cations interacting electrostatically.
Mo(CO)4L2 -Cis and Trans Isomers
There are two structural isomers for Mo(CO)4(PPh3)2, the cis and trans isomer. In order to be time efficient, the phenyl groups on this Mo complex were replaced with chloride ions, this should not make too much of a difference since they bond to the molybdenum complex in a very similar way . The only significant difference is the number of atoms being modelled and since the phenyl group is very insignificant in what we are investigating, this change can happen. The complexes were optimised three times, with three different basis sets those being LanL2MB, LanL2DZ and a corrected LanL2DZ.
Optimisation - The loose method
These isomers were optimised LanL2MB basis set with a (B3LYP method), which give a crudely optimised structure. A low value for the overall energy has been achieved however the PCl3 groups are free to move suggesting the lowest minimum has not been reached. Vibrational analysis is need to confirm if this is in fact the lowest minimum for energy.
 |
 |
|---|
Optimisation - The tight method
The tight optimisation of both isomers was then done using the LanL2DZ basis set.
 |
 |
|---|
Optimisation - The tight method (modified)
 |
 |
|---|
References
- ↑ http://hdl.handle.net/10042/to-13686
- ↑ Glaser,Johansson, Acta Chemica Scandinavica A 36 (1982) 125-135
