Rep:Mod:winder25
Characterisation of Diels-Alder Transition Structures on Potential Energy Surfaces
The Cope Rearrangement
The objective of this task was to determine the reaction mechanism of the 1,5-hexadiene Cope rearrangement. This was achieved by determining the difference between the minimum energy conformation of 1,2-hexadiene and the transition state.
Optimisation of 1,5-hexadiene
The first structure drawn (Conformer 1) had the sp2 carbon atoms 'anti' to one another. It was optimised using the Hartree-Fock/ 3-21G method; the energy was calculated to be -231.69260 Hartrees, and the point group was C2. The second structure drawn (Conformer 2) was of gauche conformation; using the same method the energy was calculated to be -231.69153 Hartrees and the point group C2.
The anti conformation was expected to be of lower energy as the sum of it's four σC-H/σ*C-H and two σC-C/σ*C-C orbital interactions are more stabilising than the two σC-H/σ*C-H, two σC-C/σ*C-H and two σC-H/σ*C-C interactions of the gauche conformation. Based on these predictions and the results above, the expected absolute lowest energy conformation around the central C-C bond was anti-; it is difficult to predict the orientation of the alkenes however. Conformational analysis suggests that in alkenes with an adjacent methyl group, the π system will orient itself at 1200 to two of the C-H bonds, leaving the third hydrogen syn-periplanar and at a good distance for van der vaals interactions with the hydrogen atom of the alkene (Diagram 1). If one hydrogen is replaced by a methyl group there are two conformers which should be very close in energy; one is Conformer 2 (already modelled) and the other has a trans-like orientation of the alkene groups (Conformer 3). Conformer 3 was modelled and optimised using the same method as before, the energy was -231.69254 Hartrees and the point group C2; as predicted, this was very close in energy to Conformer 2, although slightly higher.
The structure of the predicted lowest energy conformer was identified in Appendix 1[1] as anti1. It is the lowest energy anti- conformer but, contrary to prediction, gauche3 has the actual lowest energy - although only just. This could be explained by an attractive interaction between the orbitals of the two π systems, which may be strong enough to compensate for the reduction in attractive σC-H/σ*C-H and σC-C/σ*C-C orbital interactions.

A comparison of the HF/3-21G and DFT/6-31G was made on the annti2 (Ci) conformer. Firstly it was modelled and optimised using the method above. This calculated the energy to be -231.69254 Hartrees, and confirmed the point group was Ci. The output file for this calculation was used as the input file for the DFT/6-31G level method; the energy calculated was -234.55970 Hartrees, slightly more negative than the HF/3-21G level approximation. However, these values cannot be compared directly with any meaning as they are based on arbitrary values within the method itself. The changes in structure can be compared - the main difference is in the dihedral angle between the end four carbon atoms, this increased from 115 to 119 0 in order to increase the overlap of the orbitals calculated by the B3LYP/6-31G*; the other angles changed by less than 10. The vibrations of the molecule were then also calculated and checked for imaginary modes. None were present, as expected for a correctly optimised structure. This calculation also gave the energy of the system with corrections based on its vibrations. These are summarised in the table below; most important are the sum of electronic and zero-point energies which can be used for calculating the activation energy at 0K and the sum of electronic and thermal energies which calculates the activation energy at 298 K.
| Calculated Property | Energy (Hartrees) |
|---|---|
| Sum of electronic and zero-point Energies | -234.416252 |
| Sum of electronic and thermal Energies | -234.408952 |
| Sum of electronic and thermal Enthalpies | -234.408008 |
| Sum of electronic and thermal Free Energies | -234.447897 |
Optimisation of the Chair and Boat Transition States

Chair
The chair transition state was modelled first. This was done by combining two CH2-CH-CH2 fragments in approximately the chair conformation and using the bond modifier to ensure there was a 2.2 Å gap between the fragments. An opt+freq (Optimisation to a TS(Berny), HF/3-21G) calculation was used to optimise the molecule and calculate the frequency of vibration at the same time. The result showed one imaginary frequency, as expected, with a magnitude of 817.76 cm-1; The bond breaking/forming lengths were 2.02 Å and the total energy was -231.615191.
This transition state was also optimised using the frozen coordinate method. The redundant coordinate editor was used to initially freeze the distance between the bond breaking/forming centres at 2.2Å before an optimisation (minimum, HF/3-21G) calculation was used to minimise the energy. After this, a separate opt+freq (Optimisation to a TS(Berny), HF/3-21G) was used to find the optimum bond lengths. The calculation yielded almost identical results; the imaginary vibration had a magnitude of 818.06 cm-1, and bond lengths of 2.02 Å. The total energy was -231.619322 Hartrees, 10.85 kJ mol-1 more negative than the previous method; future comparisons used the value calculated by the frozen coordinate method.

Boat
The boat transition state was modelled using a QST2 (HF/3-21G) method. This involved drawing out the reactant and product in approximately the boat configuration (the calculation failed when the configuration was too far from a boat-like structure), then optimising using the QST2 method; this automatically generated the transition state. The imaginary vibration had a magnitude of 530.50 cm-1, the energy was -231.602802 Hartrees and the bond length 2.14 Å.
Intrinsic Reaction Coordinate
It is difficult to predict the conformation the molecule adopts in order to react via either the chair or boat transition states (TS). Gaussian was used to perform an IRC calculation, which automatically plotted the path from the transition state to the local minimum. The result for the chair TS was the gauche2 conformer and for the boat TS was the gauche3 conformer; these are the logical conformers as they require the least rotation / bond angle modification in order to form their respective transition states. The images to the left can be clicked to play a movie of the IRC coordinate path.
Calculation of the Activation Energy
The chair and boat transition structures were re-optimised using the B3LYP/6-31G* basis set.
| Model | Electronic Energy (HF/3-21G) | Electronic Energy (B3LYP/6-31G*) |
|---|---|---|
| Units | (Hartrees) | (Hartrees) |
| Gauche3 (Reactant) | -231.692661 | -234.611329 |
| Chair TS | -231.619322 | -234.556983 |
| Boat TS | -231.602802 | -234.543093 |
The table above shows there was a difference of approximately 2.9 Hartrees between the energies calculated by the two different levels of theory. This is a very large energy difference, over 7500 kJ mol-1, but it cannot be compared with experimentally determined values to see which is more accurate; the total energy cannot be determined experimentally and is based on arbitrary values built into the calculation itself. The activation energy can be determined experimentally, for the chair transition state it is 140.16 ± 2.1 kJ mol-1 and for the boat transition state it is 187.02 ± 8.4 kJ mol-1 (both at 0K).
The activation energy was calculated by finding the difference between the energy of the reactant and the transition state. The energy used in this calculation was the sum of electronic and zero point energies, as this also takes into consideration the energy from vibrational fluctuations in the ground state. The conformation chosen for the reactant was Gauche3, which had the lowest energy.
| Model | Electronic + Zero Point Energy (HF/3-21G) | Electronic + Zero Point Energy (B3LYP/6-31G*) | ΔE (0K, HF/3-21G) | ΔE (0K, B3LYP/6-31G*) | ΔE (Experimental) |
|---|---|---|---|---|---|
| Units | (Hartrees) | (Hartrees) | (kJ mol-1) | (kJ mol-1) | (kJ mol-1) |
| Gauche3 (Reactant) | -231.539486 | -234.468693 | - | - | - |
| Chair TS | -231.466696 | -234.414931 | 191.11016 | 141.152142 | 140.16 ± 2.1 |
| Boat TS | -231.450933 | -234.402340 | 232.495919 | 174.209815 | 187.02 ± 8.4 |
The HF/3-21G level of calculation would be acceptable as a first approximation, especially if time / processor power was limited; the values were of the same order of magnitude and the chair was correctly predicted to have the lowest energy barrier. The B3LYP/6-31G* level was a much better approximation; the chair activation energy was within the experimental error limit and the boat activation energy only just below.
The Diels-Alder Cycloaddition
Cycloaddition of Cis-Butadiene and Ethene
Cis-butadiene was modelled in gaussian and the structure was optimised, firstly at the Semi-Empirical AM1 level then at HF/3-21G and B3LYP/6-31G*. The HOMO and LUMO from the optimised structure were then visualised (right) and confirmed to be antisymmetric and symmetric respectively; this is consistent with literature[2]. Ethene was also optimised, and the same process was used to visualise the HOMO and LUMO, which were symmetric and antisymmetric respectively. The table below summarises the results of the energy calculations.
| Molecule | Electronic Energy | Electronic + Zero Point Energy | Electronic + Thermal Energy |
|---|---|---|---|
| cis-Butadiene | -155.986483 | -155.901141 | -155.896435 |
| Ethene | -78.587458 | -78.536232 | -78.533191 |
| Total | -234.573942 | -234.437373 | -234.429626 |
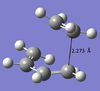
Next, the transition state of the cycloaddition was modelled and optimised using the frozen coordinate method, initially at the Semi-Empirical AM1 level then at HF/3-21G and B3LYP/6-31G*. The bond length in the TS was 2.27 Å, this is much longer than the average C-C (1.35 Å) or C=C (1.35 Å) bond; the Van der Waals radius of carbon is 1.7 Å, the fact that the forming bond length is less than this suggests the sum of the Van der Waals forces is attractive in this configuration. Both the ethene and butadiene are starting to deviate from their planar conformation in the TS, this is to minimise steric repulsion as the atoms begin to approach closer than their Van der Waals radii.
The HOMO and LUMO were visualised (right), they were antisymmetric and symmetric respectively. The shape of the HOMO of the transition state clearly showed it was a combination of the HOMO of cis-butadiene and the LUMO of ethene; the LUMO of the transition state was a combination of the LUMO of cis-butadiene and the HOMO of ethene. Both of these are combinations are of matching symmetry, and therefore allowed.
There was one imaginary vibration calculated, the reaction pathway. As the animation shows, the bonds are formed in unison - this is consistent with a pericyclic reaction. The lowest wavenumber real vibration corresponds to a translation of the molecules, it is unrelated to the bond formation.
| Molecule | Electronic Energy | Electronic + Zero Point Energy | Electronic + Thermal Energy |
|---|---|---|---|
| Transition State | -234.543895 | -234.403328 | -234.396910 |
| Ethene + cis-Butadiene | -234.573942 | -234.437373 | -234.429626 |
| Activation Energy | - | 0.034045 | 0.032716 |
| Literature [3] | - | 0.043824 | - |
The table above shows the calculated energies of the transition state. By finding the difference between the energy of the reactants and the transition state the activation energy was calculated. The result was ΔE = 89.4 kJ mol-1, this is about 20 kJ mol-1 lower than literature studies,[4] which calculate a value of 115.06 kJ mol-1 (0 K). The calculated value could have been smaller than literature because one of the reactants was not fully optimised, but they are both quite simple molecules so this is unlikely. Instead, the deviation was likely to be the result of using a different method; Houk used an MP2 method, this study used a DFT method.
Cycloaddition of Cyclohexa-1,3-diene and Maleic Anhydride
As a comparison, the endo- and exo- transition states of the cycloaddition of cyclohexa-1,3-diene and maleic anhydride were modelled and optimised. Initially this was attempted using the frozen coordinate method, but this approach proved unsuccessful. The optimisation of the transition state with bond lengths frozen at 2.2 Å was facile, but the opt+freq calculation to find the optimum bond length failed even with modifications; the first bond optimisation failed outright because several negative eigenvalues were generated and opt=noeigen was not specified. Opt=noeigen was then specified in the second attempt and a structure was generated, however there were 3 imaginary frequencies, none of which were the desired bonding vibration - this was a 3rd order saddle point. Further attempts to optimise the structure using the same method but by adjusting the initial length of the bonds returned similar results so a QST approach was taken.
QST3 was chosen over QST2 because the geometry of the transition state was known and not dissimilar to the product itself, making it easy to model. The first attempt (at the endo- TS; Semi-emp/AM1 level) of this calculation was done without optimising the geometry of the reactants or product beforehand, this failed. Once the two reactants and product were optimised to the semi-empirical/AM1 level individually and the inter-molecular bonds in the transition state were set at 2.2 Å the calculation succeeded and the endo- TS was generated; this was repeated for the exo- TS.
The calculations were also repeated using the B3LYP/6-31G* level of theory to compare the semi-empirical and density functional theory methods.
| Electronic + Thermal | Electronic + Zero Point | Electronic + Thermal | Electronic + Zero Point | |
|---|---|---|---|---|
| Semi-Emp./AM1 | Semi-Emp./AM1 | B3LYP/6-31G* | B3LYP/6-31G* | |
| endo- | -0.051505 | 0.133494 | -612.491785 | -612.502140 |
| exo- | -0.050420 | 0.134881 | -612.487662 | -612.498013 |
| Difference | 0.001085 | 0.001387 | 0.004123 | 0.004127 |
| Semi Emp./AM1 (0K) | B3LYP/6-31G* (0K) |
|---|---|
| 3.64 | 10.82 |
Both methods agree that the endo- TS is more thermodynamically stable than the exo- TS, although the B3LYP method predicted over twice the energy difference of the semi-empirical method. No reference values could be found for this reaction but a difference of over 10 kJ mol-1 is unusually large, the resulting enantiomeric excess would be greater than 99.99 %. Calculations using several other levels of theory, both semi-empirical and DFT, would have to be carried out in order to make a strong conclusion about the magnitude of the energy difference between the two transition states.

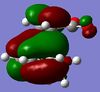
There are two possible explanations as to why the endo- TS has a lower energy than the exo- TS; the endo- may be stabilised or the exo- may be destabilised. The HOMO of the transition state was visualised first (Image Right)in order to examine it for any stabilising interactions present in the endo- but not the exo- TS. This revealed that in the endo- TS there was MO density between the sp2 carbon atoms of the anhydride and diene; this was not possible in the exo- TS. Although no bond was being formed between these atoms, they are of the correct symmetry to interact. These 'secondary orbital interactions' could explain the stability of the endo- TS, although no definitive proof of their existence has been found[5]. The interactions are more clearly demonstrated in the diagram to the left.
The theory that the exo- TS is destabilised is also credible. The interatomic distance between the carbon atoms of maleic anhydride and the hydrogen atoms attached to the sp3 centres in the diene is only ≈2.5 Å (Semi-emp. and DFT optimisation), this is within the combined Van de Waals radii of these atoms (2.9 Å) so some element of repulsion is likely; the same is true of the oxygen and hydrogen atoms. This repulsion is relieved to an extent by the longer bond between the reacting centres in the exo- TS (2.27 vs 2.29 Å, B3LYP/6-31G*), but the exo- form is more strained because of it.
Of the two explanations given above, the Van der Waals seems more plausible because these interactions have been proven to exist. However, it might be that a combination of the two is responsible for the order of stability - there is no way to tell from these calculations.
Solvent effects have been neglected by these calculations, but as the TS are structurally quite different (for example, this gives them different dipole moments) the choice of solvent may affect the selectivity. This is a possible area for future experimentation.
References
- ↑ Imperial College, 2013.
- ↑ Richard J. Loncharich , Frank K. Brown , K. N. Houk, J. Org. Chem., 1989, 54 (5), pp 1129–1134
- ↑ Houk, K. N., Li, Y. and Evanseck, J. D., Angew. Chem. Int. Ed. Engl., 1992, 31: 682–708
- ↑ Houk, K. N., Li, Y. and Evanseck, J. D., Angew. Chem. Int. Ed. Engl., 1992, 31: 682–708
- ↑ José I. García , José A. Mayoral , Luis Salvatella. Acc. Chem. Res., 2000, 33 (10), pp 658–664.