Rep:Mod:will12345
Transition states Computational
The Cope Rearrangement Tutorial
The Cope rearrangement involves the [3,3] sigmatropic rearrangement of 1,5 dienes. The reaction is part of the pericyclic family, and is widely acknowledged to be concerted in nature, with bond making and bond breaking occurring in a single step (This is a conjecture that you can confirm with these calculations. João (talk) 20:36, 12 February 2015 (UTC)). As the rearrangement is classified as a pericyclic reaction, and thus is subject to Woodman-Hoffman selection rules as to weather the process is an allowed rearrangement. The process involves a rearrangement of 4n+2 electrons ( in this case a six electron system), and thus can be promoted with heat, to give a suprafacial stereo chemistry in the product via a Huckel transition state, or can be promoted with light to give an antarafacial component via a Mobius transition state. Although the Cope rearrangement refers to the general rearrangement of 1,5 dienes, thy system chosen to model the rearrangement is based around a 1,5 hexadiene system.

To successfully model the Cope rearrangement computationally, a molecule of 1,5 hexadiene was optimised. The output structure alongside the calculation parameters are included below:
| 1,5 hexadiene | ||||
| Jmol |
| |||
| File Type | .log | |||
| Calculation Type | FOPT | |||
| Calculation Method | RHF | |||
| Basis Set | 3-21G | |||
| Charge | 0 | |||
| Spin | Singlet | |||
| E(RB3LYP) / a.u. | -231.69260 | |||
| RMS Gradient Norm / a.u. | 0.00001296 | |||
| Imaginary Freq | ||||
| Dipole Moment / Debye | 0.2021 | |||
| Point Group | C1 (C1 point group corresponds to the absence of symmetry, still your structure seems quite symmetric. How does the structure compare with the ones give on experiment script? João (talk) 20:36, 12 February 2015 (UTC)) | |||
| Job cpu time | 0 days 0 hours 0 minutes 5.0 seconds. |
An optimised structure from a Guassian output file can be manually checked to ensure the calculation has provided a minima and not a transition state via analysis of the log file (You can check on the log that the gradient has converged to zero and you found a stationary point on the potential energy surface, but how do you know if this point is a minimum or a transition state or something else? João (talk) 20:36, 12 February 2015 (UTC)). A fully converged calculation will be shown within this file, and an example of a successfully converged optimisation is shown below:

From this point on it can be assumed that any optimisation calculation performed converged successfully, without an extract from the log file being directly included as above.
The calculation successfully converged to a minimum value, but chemical intuition (Is a local minimum on a surface a subject in the realm of chemical intuition? João (talk) 20:36, 12 February 2015 (UTC)) would suggest that further analysis is required. Free rotation about numerous bonds within the structure leads to potential gauche or anti conformations at numerous points. Stereochemical effects are certainly well known to influence the energetics of given molecules, for example the prevalent gauche effect in 1,2 difluroethane, or the anomeric effect in substituted sugars leading to an axial preference for substitution. To analyse the 1,5 hexadiene system, a gauche conformation was subjected to an optimization calculation:
| 1,5 hexadiene | ||||
| Jmol |
| |||
| File Type | .log | |||
| Calculation Type | FOPT | |||
| Calculation Method | RHF | |||
| Basis Set | 3-21G | |||
| Charge | 0 | |||
| Spin | Singlet | |||
| E(RB3LYP) / a.u. | -231.69166701 | |||
| RMS Gradient Norm / a.u. | 0.00001086 | |||
| Imaginary Freq | ||||
| Dipole Moment / Debye | 0.3805 | |||
| Point Group | C1 (See comment about symmetry above. João (talk) 20:36, 12 February 2015 (UTC)) | |||
| Job cpu time | 0 days 0 hours 0 minutes 32.0 seconds. |
The relative energies of the gauche and anti conformers can be analysed, but one has to consider the accuracy of the Gaussian optimisation when doing so. The approximate error range for a given Gaussian optimization is 10k kJ/mol (Using which method? Where did you find this estimate? João (talk) 20:36, 12 February 2015 (UTC)). Converting this to Hartree ( a.u) and we obtain a discrepancy of 0.00381 a.u. Given that the differences within the isomers optimized is 0.00093 au, an energetic comparison is technically unjustified given that the gauche and anti conformers both give energy values that fall within the error range of the program- technically they should be viewed as degenerate. At this point it becomes difficult to take the problem further. Simple chemical intuition would lead to the belief that there is a global minimum structure for the hexadiene structure, but to the accuracy of the Gaussian protocols, this minima is impossible to conclude. There are no overwhelming factors that could lead to a fully justified statement favouring one conformation over another. The problem has been eluded to in the literature, and is still debated, and not universally agreed upon. Perhaps the most valid conclusion that can be made at this point is that there is a global minima, but the computational method to obtain is was not available. http://pubs.acs.org/doi/pdf/10.1021/ja00111a016
Calculating Thermodynamic information- a case study
To further explore the potential of the Gaussian program, a specific anti conformation of 1,5 cyclohexadiene was chosen, and the resultant conformation minimised using identical methodology to the previous calculations. An identical molecule was then optimised using a differing basis set, and the difference in energies led to an interesting comparison (You are both using a different basis set (3-21G) and a different method to calculate the electronic energy (Hartree-Fock). João (talk) 20:36, 12 February 2015 (UTC))
| Isomer | Hartree Fock calculation | DFT calculation | ||||||
| Jmol |
|
| ||||||
| File Type | .log | .log | ||||||
| Calculation Type | FOPT | FOPT | ||||||
| Calculation Method | RHF | RB3LYP | ||||||
| Basis Set | 3-21G | 6.31G | ||||||
| Charge | 0 | 0 | ||||||
| Spin | Singlet | Singlet | ||||||
| E(RB3LYP) / a.u. | -231.69253530 | -234.55970458 | ||||||
| RMS Gradient Norm / a.u. | 0.00000751 | 0.00004297 | ||||||
| Imaginary Freq | ||||||||
| Dipole Moment / Debye | 0 | 0 | ||||||
| Point Group | Ci | Ci | ||||||
| Job cpu time | 0 days 0 hours 0 minutes 38 seconds. | 0 days 0 hours 0 minutes 42.0 seconds |
Upon examination of the relative energies of the above structures, the DFT calculation provides a structure that is lower in energy than the HF calculation (Although true, this is meaningless as one cannot compare absolute energies obtained with different methods (as these use different references), see for example values obtained with semi-empirical methods. It is although legitimate to compare relative energies obtained with different methods. João (talk) 20:36, 12 February 2015 (UTC)). Inferring from structural data obtained from Gaussian, the DFT produces a structure in which the dihedral angles are greater than that of the HF calculation ie the carbon carbon linkages through the chain are closer to an anti periplanar linkage in the DFT calculation than in the HF. The overall symmetry of the structures remains unchanged however on alternating the basis sets, with both giving Ci point groups.
An alternative method to confirming a minimum has been obtained (It is not an alternative, it is a requirement. João (talk) 20:36, 12 February 2015 (UTC)), other than directly checking convergence in the log file is to run a frequency calculation on the optimised structure, and confirm that all frequencies are real ( no imaginary vibrations). Performing a frequency analysis has the added benefit of the ability to provide thermodynamic data from the optimisation. The current 'minimum' energy conformation of the optimised molecule is representative of the bare potential energy surface alone. Performing a frequency calculation allows the calculation of some thermochemical properties.


Thermodynamic data obtained:
(How do these quantities vary with temperature? João (talk) 20:36, 12 February 2015 (UTC))
| Quantity | Value (Ha) |
|---|---|
| Sum of electronic and zero point Energies | -234.416259 |
| Sum of Electronic and thermal Energies | -234.408966 |
| Sum of Electronic and Thermal Enthalpies | -234.408021 |
| Sum of free energies | -234.447881 |
Optimizing the 'chair' and the 'boat' transition states
Working towards the chair transition state
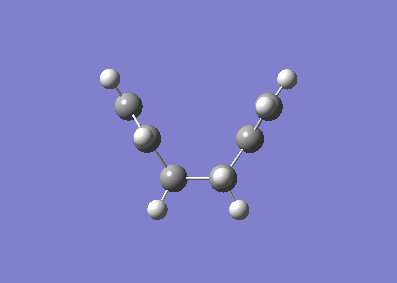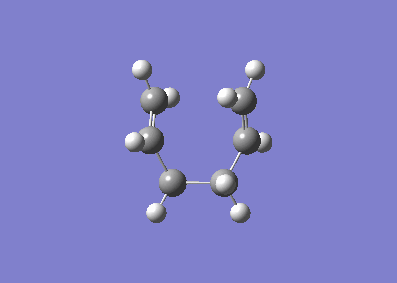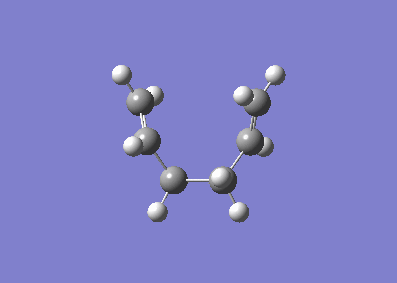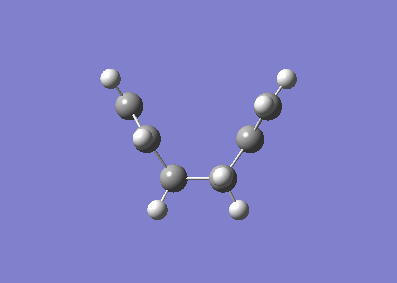
The transition state for the Cope rearrangement can be visualised to either pass through a chair or a boat transition state on the reaction path to the product molecule. An initial guess at the chair like transition state was created using two optimised allyl fragments. In contrast to earlier calculations, it was hoped the output frequencies would contain an imaginary frequency, which would correspond to the transition state along the reaction coordinate. The imaginary frequency believed to correspond to the transition state is visualised below:
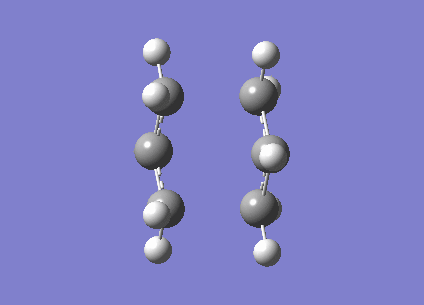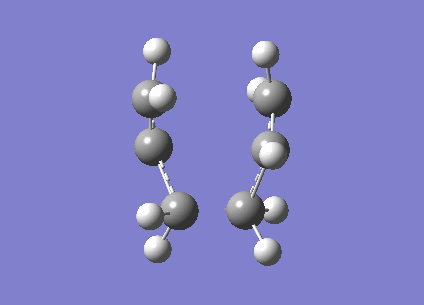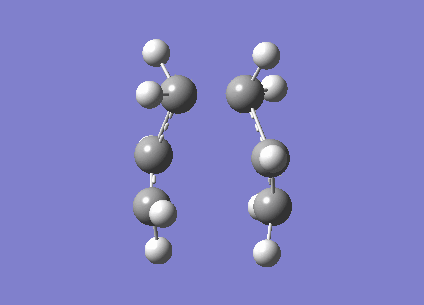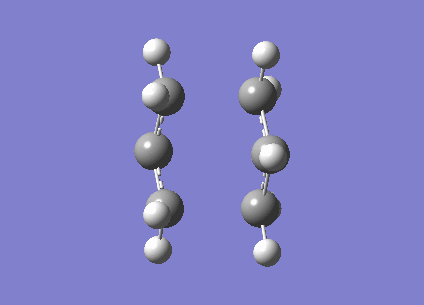
Completed using a HF 3-21G basis set
In order to ensure the above calculation completed successfully the 'guess' transition structure input had to be close in structure to the actual transition state. To try and avoid errors, the input line Opt=NoEigen was added to the calculation, to avoid termination if two imaginary frequencies were located by the program. If the two allyl fragments were positioned too far apart, the program misinterpreted the calculation, often leading to the formation of a gauche conformer (This is actually an interesting and illustrative observation. It shows why one needs to check the nature of the stationary point after an optimization, especially when the imaginary frequency tests were switched off as in your case. João (talk) 20:36, 12 February 2015 (UTC)). Only in the case where the terminal carbons of the allyl fragments were positioned 2Ã
apart did the calculation run smoothly.
An alternative method is a available to calculate transition states, and is based on the idea of freezing coordinates, ie rendering atoms immobile. This method was invoked and a second transition state calculated, based around a frozen bond length of 2.2Ã between the terminal carbons where the bond forming takes places. This distance was gauged from the previously calculated transition structure above, and hence should closely resemble the transition state.
Models of the two optimised chair transitions states are listed below, along with key structural comparison data
| Isomer | Hartree Fock calculation | Frozen Co-ordinate calculation | ||||||
| Jmol |
|
| ||||||
| Terminal C-C bond length (Ã ) | 2.0202 | 2.02117 | ||||||
| C-C-C angle within fragment | 120.518 | 120.50 |
Once again when comparing these structures, the accuracy of the computational method used must be considered: bond length values are accurate to 0.01 Ã
, and bond angles to about 0.1°. To the accuracy of the method used, these transition structures are essentially identical, the use of two different methods is simply to illustrate the varying computational methods available. The two methods will differ appreciably in larger scale calculations, perhaps in computational cost and in the relative difficulty of setting up the calculation.
Working towards the boat transition state
To work towards the boat transition state, a third potential method of calculation will be explored. Previously an attempt to find the transition state structure was attempted via directly building and optimizing a structure believed to be close to the transition state, ie there was no consideration of the initial and final state of the system. An alternative method involves building the initial and final states of the system, and asking Gaussian to find a transition state between them. This method has the added benefit that it is no longer necessary to 'guess' transition structures. Although we have been able to make reasonable guesses thus far for our simple system, it is likely that as the system becomes more complex, with additional factors such as sterics and secondary orbital effects and a host of others being introduced, it becomes exponentially harder to make a good 'guess' transition structure.
The calculation method invoked for this level of optimisation involves the QST2 basis set (QST2 is not a basis set (neither a method to calculate electronic energy), but rather a method to find transition state structures. You can read about how it works from the Gaussian online manual. João (talk) 20:36, 12 February 2015 (UTC)), and in order for the calculation to proceed smoothly, Gaussian requires the reactant and the product to be labelled (In this type of calculations, atoms are always labelled. In this case you need to label them in a consistent manner with the chemical reaction you are studying. João (talk) 20:36, 12 February 2015 (UTC)), allowing the calculation to find the atoms around which bond breaking and bond forming is occurring. An example of the reactant and product labeling is shown below:
In initial optimisation of the system using the QST2 protocol failed, producing a structure that was not representative of a transition state (Was it not a transition state, even if not the one you wanted to obtain? João (talk) 20:36, 12 February 2015 (UTC)). in order to yield a transition state, the initial reactant and product molecules had to be modified, in order to bring them closer to what is believed to be a transition state. This of course returns us to the previous problem of what happens if we don't know what the transition state looks like (True point. Computers cannot do all the work by themselves yet. João (talk) 20:36, 12 February 2015 (UTC)). Although for this system the transformations involved changing the dihedral angle along the carbon chain to 0, and modifying the internal angle towards 100 degrees. The changes necessary are summarized below, along with the vibration corresponding to the boat like transition state, and the optimised transition state structure.
Analysing the IRC
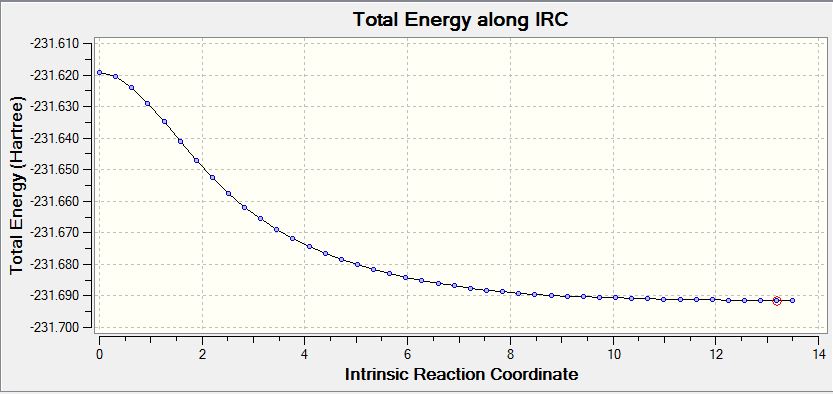
Working along the potential energy surface in search of the region of steepest descent represents a methodology that can find a local minima. Examining the boat and chair transition structures above, it is very difficult to establish exactly which conformer of the 1,5 hexadiene leads towards the transition state. Thus, a potential method to solve this issue is to use the IRC in an attempt to track the reaction back to the reactant conformation (or indeed the product conformation in this case as the reactants and products are identical). An IRC calculation was run using a HF 3-21G basis set, firstly on the chair transition structure. the energy profile along the IRC as well as a visual representation is shown below:
The above calculation was performed over 50 steps, with the minimum structure then subjected to an optimization to a minimum using HF 3-21G. The structure pictured below could thus be expected to be the reactive conformation of the 1,5 hexadiene molecule, with energy of -231.69166702 Ha, although this differs slightly to the final energy of the IRC ( -231.69157716 Ha). Within the error range of the program, it is possible to conclude that the conformer that leads to the transition state is the gauche conformer shown below:
Reactive conformation of 1,5 hexadiene |
Obtaining activation energies for the Cope rearrangement
| Structure | HF/3-21G Electronic Energy ( Ha) | HF/3-21G Sum of Electronic and Thermal Energies at 0K (Ha) | HF/3-21G Sum of Electronic and Thermal Energies at 298.15K (Ha) | B3LYP/6-31G Electronic Energy ( Ha) | B3LYP/6-31G Electronic and Thermal Energies at 0K (Ha) | B3LYP/6-31G Electronic Energy and Thermal Energies at 298.15K (Ha) |
| Chair | -231.61932128 | -231.466686 | -231.461340 | -234.556929 | -234.41912 | -234.408987 |
| Boat | -231.6028021 | -231.450930 | -231.445311 | -234.543088 | -234.402351 | -234.396008 |
| Anti-2 | -231.69253530 | -231.539535 | -231.532567 | -234.611711 | -234.469206 | -234.461860 |
| Structure | Activation energy at OK HF/3-21G | Activation energy at 298K HF/3-21G | Activation energy at 0K B3LYP 6-31G | Activation at 298K B3LYP 6-31G | Experimental (0K) [1] |
| Chair | 45.7134474 | 44.69562685 | 31.429446228 | 33.1783155 | 33.5 ± 0.5 |
| Boat | 55.60048882 | 54.7539784 | 41.9521548 | 41.3227627 | 44.7 ± 2.0 |
(You report above transition state structures optimized at the B3LYP/6-31G* level of theory. How does the transition state geometry change at this level of theory? Does it conserve one imaginary frequency? João (talk) 20:36, 12 February 2015 (UTC))
Diels Alder reaction of Butadiene and Ethene- a case study
Theory of the Diels Alder Reaction
In the following sections, an example of Diels Alder reaction involving butadiene and ethene is analysed. The Diels Alder is an extremely important reaction in organic chemistry, and can be invoked to form a wide range of products, many of which find uses in pharmaceutical applications. The following section examines the most elementary Diels Alder reaction between butadiene and ethene.
Beginning the calculation: In order to optimise to a transition state, butadiene and ethene were optimised under the semi empirical AM1 basis set (AM1 is not a basis set. It is a semi-empirical method to calculate the electronic energy (similar to the HÃŒckel method), and uses a minimal basis set. João (talk) 20:36, 12 February 2015 (UTC)) to yield minimum energy structures. These optimised structures were then used within Gaussian to generate an approximate transition state geometry. The geometry of the predicted transition state is shown below:
Approximate transition state |
The above structure represents the 'guess' geometry that led to a successful calculation. In the case of the input geometry of the 'guess' not being close enough in structure to the actual transition state, Gaussian terminates giving a general error message describing an incorrect input geometry. The guess structure was then subjected to an optimization to a Berny transition state, calculating force constants once. The output structure successfully visualises the transition state structure via the imaginary frequency vibration (click to view the vibration):
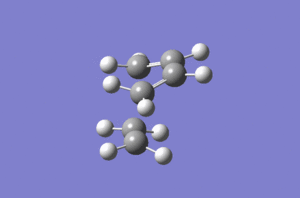
Parameters of the transition state
Before listing the parameters, it seems important to classify exactly what we expect to find, if this is a transition state, and how bond lengths represent any significance. If a transition state is an intermediate between the products and reactants, we can examine some parameters of the starting materials, and consider how they might change on the way to the products. For example, we could reasonably expect the double bond in the ethene molecule to be lengthening - the transition state will represent an intermediate between sp2 and sp3 geometry and hence as the reactant coordinate progresses, the bond should be getting progressively closer to an sp3 like bond distance. An analogous justification can be considered for the double bonds of the butadiene system. Perhaps this is also a good point to invoke Hammonds Postulate, and consider if invoking it will lead to any interesting assumptions. Hammonds postulate states that species with similar energies along the reaction coordinate have similar structures. Thus in analysing the transition state we may be able to get an idea of the magnitude of the activation energy: if the transition state shows sp2 bonds that are very close to pure sp2 in character (ie are close to the C=C length in isolated ethene), the transition state could be assumed to be close in energy to the reactant. Given that Diels Alders often proceed extremely efficiently, a chemists intuition would predict that there will be very little structural change from the isolated reactants to the transition state. Some key parameters from the transition state structure are given below:

| Bond | Value (Amstrongs) | Isolated value (if applicable) [2] |
|---|---|---|
| C11-C12 | 1.38290 | sp2=1.34. sp3=1.54 |
| C4-C12/C1-C11 | 2.11937 | - |
| C4-C3/C2-C1 | 1.38185 | 1.34 |
| C2-C3 | 1.39749 | - |
As can be seen from the above data, the transition state represents only a very small increase in the sp2 bond lengths compared to that of isolated species. The predicted made earlier, that the transition state is seemingly very close in energy to the reactants seems to be valid. Also of note is the identical nature of the bond lengths, the transition state has the ethene approaching equally towards each terminal carbon of the butadiene, and the vibration shows that this bond forming is synchronous (concerted). Perhaps the most interesting part is examining the value of the bond forming distance (between the terminal carbons of the butadiene and the ethene fragment. This value is clearly over that of any appreciable true bond, and thus at most these carbons may be interacting in the transition state, but there is certainly no justification for drawing a formal bond between these atoms. In considering weather an interaction is taking place it is common to invoke Van de Waals radii of the contributing atoms. In the literature, carbon is reported as having a radii distance of 1.7A. Given that twice the Van de Waal radii is seen as the limit for any sort of interaction, the value of 2.12A in the transition state is a clear indication that the atoms have begun to interact, and are experiencing attractive forces and can be considered to be partially bonding.
(Nice discussion of the geometry changes occurring in the vicinity of the transition state. João (talk) 20:36, 12 February 2015 (UTC))
Orbitals involved in the transition state Discussion
An orbital consideration can allow a chemist to predict weather or not a reaction will take place. As mentioned previously, Woodward-Hoffman rules can be used to predict if a pericyclic reaction ( of which Diels alder belongs) will take place, with rules based around symmetry considerations. The Diels Alder is a 4n+2 electron process, and is thermally allowed using the Woodward Hoffman rules. Considering if a reaction is allowed is one aspect, but one must also consider if an allowed reaction will actually happen. In order for a reaction to take place, the HOMO and LUMO of the molecules must be able to interact ( this is both a symmetry and energetic concern) and this means they must possess the same symmetry. HOMO/ LUMO surfaces were generated for the butadiene molecule, with the results shown below:

HOMO of butadiene(antisymmetric with respect to the plane)

LUMO of butadiene(symmetric with respect to the plane)
The above MO's are made up of constituent AO's as shown below

Contributing AO's that form MO's
The frontier orbitals of ethene were not calculated due to their simplicity- the HOMO is the symmetric pi orbital formed from two in phase p orbitals, and the LUMO the asymmetric antibonding orbital. Given this consideration, it is thus justifiable that in this reaction the HOMO of butadiene is able to act with the LUMo of the ethene. This fulfills the general Diels Alder consideration of the HOMO of the diene interacting with the LUMO of the dieneophile. This interacting is justified through symmetry, but could also be tuned by adding substituents such as electron withdrawing groups to the dienophile to bring the frontier orbitals closer in energy.
Given that the orbital considerations on the individual components have the correct symmetry elements to react, the molecular orbitals for the transition state were calculated, with both the calculated orbitals, and the AO contributions shown below:

LUMO (symmetric) of the transition state

HOMO (asymmetric) of transition state

AO contributions to the transition state MO's
The above results confirm the orbitals involved in producing the transition state structure. Using qualitative MO theory, one could actually predict these structures by combination of atomic orbitals by combining the orbitals in the two atomic orbital diagrams and considering constructive and destructive interference.
Diels Alder reaction of cyclohexa-1,3-diene and maleic anhydride- a case study
Theory
The Diels Alder reaction between cyclohexa-1,3-diene and maleic anhydride is again a 4n+2 pericyclic process, and can be promoted thermally via the Woodward Hoffman rules. Analogous to the previous Diels Alder case study the symmetry of the frontier orbitals must be considered in order to assess if a reaction will occur. In order to calculate the transition state, molecules of cyclohexa-1,3-diene and maleic anhydride were first individually optimised, with the resulting geometries shown below:
|
|
|---|
Unlike the previous case study which utilised ethene as the dieneophile, the maleic anhydride can produce more than one possible transition state, dependent on its orientation relative to the diene. The transition states are often denoted endo and exo, with the endo state almost always being more stable, often referred to as the Alder endo rule within the literature. Below are the two possible orientations of approach for the reaction:
|
|
|---|
In order to predict the relative energy levels of the transition state, a frontier orbital analysis is once again required (It is fine to make this qualitative prediction a priori, but note that the calculation is doing exactly this work for you. João (talk) 20:36, 12 February 2015 (UTC)). As per the first case study, the HOMO of the diene must be of the same symmetry as the LUMO of the dieneophile. Using the AM1 semi-empirical basis set the HOMO and LUMO for both the diene and the dienophile were generated, and are pictured below:

HOMO of maleic anhydride

LUMO of maleic anhydride

HOMO of cyclohexadiene.

LUMO of cyclohexadiene
Although the above are useful in determining the overall contributions of the atomic orbitals in producing the molecular orbitals, they are somewhat difficult to visualise, and thus justifying the stability of the endo transition state is not greatly aided by these models. Constituent AO diagrams are a clearer more concise way to explain and solve the problem:

AO concept of transition state
Although not particularly clear, the above diagram aims to show how the orientation of the dieneophile can effect what orbital interactions can take place. In the endo transition state, there is a favourable potential through space interaction between the dieneophile and the back carbons of the diene that is not present in the exo transition state. The in phase combination is a favourable interaction, and acts to lower the energy of the endo transition state relative to the exo. For this reason, unless in cases of extreme steric bulk, the Alder endo rule is nearly always adhered to.
Is the secondary orbital actually there?: Carrying out the transition state calculations
The transition states were calculated using an AM1 semi empirical basis set, and the imaginary frequencies are visualised below
| Structure | 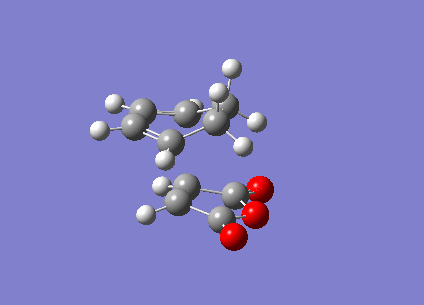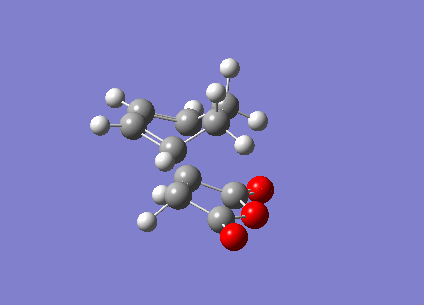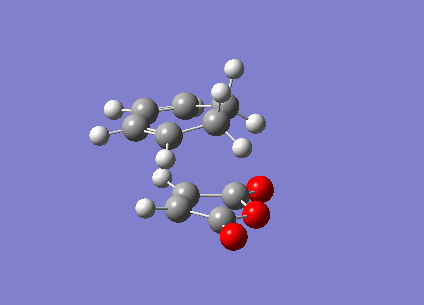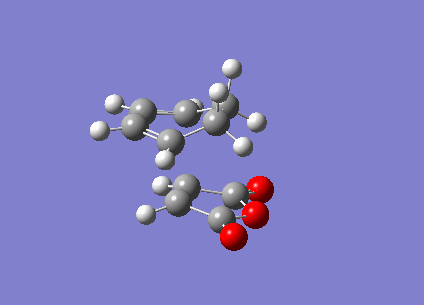 |

|
|---|---|---|
| Transition state | Exo | Endo |
The difference in geometry within the transition state structures is clear, but in order to determine if a secondary orbital interaction is actually present, the energy of the respective states needs to be examined: (If you are interested in an orbital effect, why not looking at the orbitals themselves instead of the energy? João (talk) 20:36, 12 February 2015 (UTC))
| Transition state | Exo | Endo |
|---|---|---|
| Energy (a.u) | -0.05041981 | -0.05150441 |
| Relative Energy (kJ/mol) | +2.84761752 | 0 |
| Frequency | -812.21 | -806.39 |
The relative energies of the transition states confirm that the endo state is indeed lower in energy by approximately 3kJ/mol relative to the endo transition state. This means the energy barrier of the forward reaction passing over the endo transition state is reduced relative to the exo, and hence this lower activation energy would lead to an endo dominated addition product (Would this not depend on the reaction conditions? João (talk) 20:36, 12 February 2015 (UTC)).
Parameters of the transition state
Some key bond lengths of both the exo and endo transition state is listed below. it is likely that the exo transition state suffers less from steric repulsion compared to endo, but the endo is electronically favoured due to the secondary orbital overlap.
| Structure |  |
 |
|---|
| Exo bond | Value (Amstrongs) |
|---|---|
| C5-C14 | 2.17051 |
| C14-C13 | 1.41011 |
| C4-C14 | 2.83380 |
| C6-C14 | 2.63510 |
| Endo bond | Value (Amstrongs) |
|---|---|
| C4-C13 | 2.72331 |
| C5-C18 | 2.20536 |
| C6-C18 | 2.13480 |
| C6-C1 | 1.39685 |
| C13-C14 | 1.41011 |
Key bond parameters from within this data include that the bond forming distance is longer in the endo than the exo. This could be rationalised by considering that the endo transition state may have an increased steric requirement, and hence is less able to approach the diene (What would Hammond have to say about that? João (talk) 20:36, 12 February 2015 (UTC)). This justification gains further weight when it is considered that the endo product is a kinetic product, the exo product is actually the thermodynamic product of the reaction, and thus is the energetically more stable product, possible due to the decreased steric strain within the product formed via the exo transition state. Similar to the previous case study, the double bonds within the reactants are expanding as the transition state is approached, becoming more delocalised in nature, as the C-C bond lengths within the diene structure begin to equate towards sp3 structures.
Exo v Endo Product structures
| Isomer | Exo | Endo | ||||||
| Jmol |
|
| ||||||
| File Type | .chk | .chk | ||||||
| Calculation Type | FOPT | FOPT | ||||||
| Calculation Method | RB3LYP | RB3LYP | ||||||
| Basis Set | 6-31G | 6.31G |
Although the secondary orbital overlap effect is theoretically possible, and the energies are certainly suggestive that some stabilisation of the endo transition state has taken place, visualising the HOMO and LUMO orbitals for both the exo and endo transitions states is inconclusive:
| Transition state | HOMO | HOMO side view | LUMO | LUMO side view |
|---|---|---|---|---|
| Exo |  |
 |
 |
 |
| Endo |  |
 |
 |
 |
As can be seen from the above images, the presence of the secondary orbital overlap is not present in the endo structure. Although the theory behind the secondary overlap seems sound, it is possible that errors within the Gaussian calculation lead to this factor being neglected (Why would the method you are using be making a greater error than the qualitative argument? João (talk) 20:36, 12 February 2015 (UTC)). The source of this error could be as simple as the transition state structure not having the exact correct geometry. For example if the diene and the dieneophile do not approach with close enough proximity then the secondary orbital overlap may be neglected by Gaussian (Is it neglected or simply insignificant? João (talk) 20:36, 12 February 2015 (UTC)). other issues may include Van der Waals interactions and hydrogen bonding effecting the geometry of the transition state (Are you thinking about the reaction in solution? João (talk) 20:36, 12 February 2015 (UTC)).
Perhaps if one truly wanted to ( perhaps falsely) identify the secondary orbital overlap, analysing the side on HOMO structures from both of the endo and exo structures, the endo appears more sweeping in nature, ie the shape of the orbital appears as though it has a greater component angled towards where the secondary orbital overlap would be expected. Although this would likely be a step too far in terms of claiming that this is definitely the secondary orbital overlap, it could certainly be a contributing factor.
Conclusions
In conclusion the computational methods have proved extensively useful in determining transition state structures in Diels Alder reactions. It has been shown that the endo transition state in Diels Alder reactions is kinetically favoured, proceeding through a lower activation barrier than the exo transition state. Although this was hypothesised to be due to the secondary orbital overlap present in the endo structure, this was unable to be confirmed using the level of calculation present within the Gaussian program. Gaussian is able to easily optimise to a transition state when the structure can be easily hypothesised, but greater complications may be experienced on larger scale systems, where there are both more variables in any transition state, and it may be difficult to provide a 'guess' accurate enough for Gaussian to be able to generate a transition structure.
<references> <ref name="script"> Michael Bearpark Laboratory script: accessed at: https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3
<ref name="van der waals radii"> Fox, Marye Anne; Whitesell, James K. (1995). Organische Chemie: Grundlagen, Mechanismen, Bioorganische Anwendungen. Springer