Shahania Begum

Module 3 Physical computational lab

Transition states

For the following set of computational experiments, the transition structures in larger molecules have been explored. Molecular orbital-based methods, numerically solving the Schrodinger equation, and locating transition structures based on the local shape of a potential energy surface have been used to describe bonds being made and broken, and changes in bonding type / electron distribution. As well as showing what transition structures look like, reaction paths and barrier heights have also been calculated.

Exercises

The Cope rearrangement of 1,5-hexadiene has been studied as an example of a chemical reactivity problem.

The low-energy minima and transition structures on the 1,5-hexadiene's potential energy surface were located in order to determine the preferred reaction mechanism.

This [3,3]-sigmatropic shift rearrangement occurs in a concerted fashion via either a "chair" or a "boat" transition structure, with the "boat" transition structure lying several kcal/mol higher in energy.

The B3LYP/6-31G* level of theory, is later used to reproduce activation energies and enthalpies which are in remarkably good agreement with experiment.

The Cope rearrangement tutorial

In GaussView, a molecule of 1,5-hexadiene with an "anti" linkage for the central four C atoms was constructed and the structure was cleaned then optimised using the HF/3-21G level of theory. The energy and the point group of this structure were noted;

Anti 1,5-hexadiene

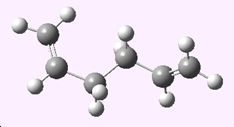Energy a.u

-231.69097

Point group

C₁

Another molecule of 1,5-hexadiene with a "gauche" linkage was created. Again the structure was optimised using the HF/3-21G level of theory and the point group symmetry was recorded.

Gauche 1,5-hexadiene

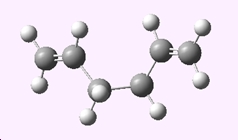Energy a.u

-231.69153

Point group

C₂

From comparing the energies of the "anti" and "gauche" conformers initially it would be expected that the gauche conformer would be lower in energy due to the additional stabilisation caused by hyperconjugation and bent bonds from the overlapping orbitals-the Gauche effect. The energy of the Gauche conformer is -231.96153 a.u, with a point group of C₂ symmetry. The anti conformer has an energy of -231.69097 a.u. From comparing the final energies of the optimised anti and gauche conformers it can be seen that the Gauche conformer has a slightly more negative energy than the anti conformer rendering it more stable with the lower energy.

Calculated activation energies and enthalpies normally use the lowest energy conformation of a reactant molecule as a reference. Based on the above results, it could be predicted that the lowest energy conformation of 1,5-hexadiene might be a gauche conformation perhaps with the double bonds anti-symmetric with respect to each other rather than parallel in the example above.

This hypothesis was tested out below;

Gauche 1,5-hexadiene (hypothesis test)

Energy a.u

-231.69167

Point group

C₂

It appears as thought the hypothesised gauche structure is slightly more stable with a lower energy than the first gauche structure. However this is still not the lowest energy ocnformaton possible. From comparing the conformers of 1,5-hexadiene and their point groups in [Appendix 1]. The energies and point groups match up exactly, The anti structure above is the anti4 conformer, the gauche structure is gauche4 and the hypothesised structure is gauche2. As there are so many conformers, depending on whether the anti1 conformer was first optimised and compared the proposed hypothesis would not have been viable as this anti conformer is lower in energy thatn gauche4. However overall it is gauche 3, with an energy of -231.69266 a.u which is the lowest energy conformation. Perhaps this is due to the anti-symmetric nature of the conformer providing the best overlap for the Gauche effect.

The anti2 conformer was optimised at the HF/3-21G level of theory;

Anti2 1,5-hexadiene
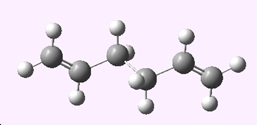	Energy a.u
-231.69254
Point group
C_i

From comparing the final energies of the Anti2 configuration with C_i symmetry to that given in the appendix the energies obtained are identical at -231.69254 a.u.

After reoptimizing the Anti2 structure using the DFT method, at B3LYP/6-31G (d) level. At this higher level of theory the energy obtained was -234.61171 a.u, this energy is lower in energy compared to the energy obtained from the HF/3-21G calculation. The geometry/point group remains Ci and the overall geometry did not change.

From the optimized B3LYP/6-31G* structure, the frequency calculation was computed. ppear. There were no imaginary frequencies, the IR spectrum of anti2 can be seen below.

The following energies were obtained from the output file;

Type of energy	Energy a.u
Sum of electronic and zero-point Energies	-234.469176
Sum of electronic and thermal Energies	-234.461834
Sum of electronic and thermal Enthalpies	-234.460890
Sum of electronic and thermal Free Energies	-234.500743

The first of these is the potential energy at 0 K including the zero-point vibrational energy (E = Eelec + ZPE), the second is the energy at 298.15 K and 1 atm of pressure which includes contributions from the translational, rotational, and vibrational energy modes at this temperature (E = E + Evib + Erot + Etrans), the third contains an additional correction for RT (H = E + RT) which is particularly important when looking at dissociation reactions, and the last includes the entropic contribution to the free energy (G = H - TS).

The above energies and those obtained via the HF method have been compared below;

Summary of energies (in hartree)

	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
anti2 results	-231.692535	-231.539542	-231.532571	-234.611712	-234.469176	-234.461834
Literature anti2	-231.692535	-231.539539	-231.532566	-234.611710	-234.469203	-234.461856

From comparing the values obtained to the experimental values obtained from those in the appendix it can be seen that these results are easy to reproduce only varying in the 5th decimal place however this is probably due to error and calculations only being accurate to ~1kJ/mol, 4 d.p for a.u.

Optimizing the "Chair" and "Boat" Transition Structures

The "chair" and "boat" transition structures for the Cope rearrangement were created below. Each consisting of two C3H5 allyl fragments positioned approximately 2.2 Å apart, one with C2h symmetry and the other with C2v symmetry.

The "Chair" transition state

For the chair transition state, the ally fragments were drawn as single fragments initially and optimized using the HF/3-21G level of theory. After which they were copied and pasted to create a new molgroup.

The transition state was optimised and the force constant matrix (the Hessian)was computed via method one; a TS Berny optimization.

The job was sucessful in producing only one imaginary frequency of magnitude 817.938 cm-1 corresponding to the Cope rearrangement as can be seen below.

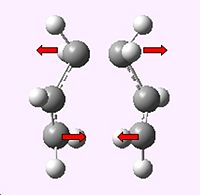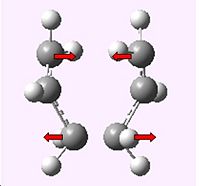The transition state was then optimised again from a newly created transition structure using the frozen coordinate method. This time the Redundant Coord Editor was used to freeze and the length of the forming/breaking bond was specified at (2.2Å). With additional keywords Opt=ModRedundant.

From this preoptimised structure the two frozen coordinates were also optimised, using a normal guess Hessian which was modified to include the information about the two coordinates which were being differentiating along.

TS Berny method	Hessian method

Forming/Breaking bond length (Å)	Forming/Breaking bond length (Å)
2.2	2.2

From comparing the forming/bond breaking bond lengths of that obtained from the TS Berny optimisation and the Hessian optimisation, the bond lengths for both are the same at 2.2Å, after all this would be expected as they were specified to be that length in the Hessian method and they were fixed in the TS Berny method, this suggests that the first guess structure was a good approximation.

The "Boat" Transition state

The Boat transition structure was optimised using the QST2 method. Where the reactants and products for a reaction were specified and the calculation interpolated between the two structures to try to find the transition state between them. The numbering of the 1,5-hexadiene product and reactants were manually changed.

After submitting the calculation, initially the job failed as it looked a bit like a more dissociated version of the chair transition state. The original input file was then modified so that the reactant and product geometries looked closer to the boat transition structure.

The job was sucessful, it had converged, producing only one imaginary frequency at -839.717cm-1 is seen, with the following motion displayed below;

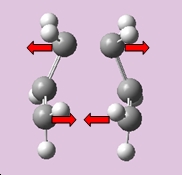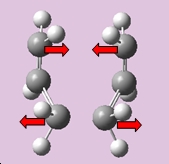This exercise demonstrates that although the QST2 method has some advantages because it is fully automated, it can still often fail if the reactants and products are not close to the transition structure.

Intrinsic Reation coordinate method

The IRC method follows the minimum energy path from a transition structure down to its local minimum on a potential energy surface. A series of points are created by taking small geometry steps in the direction where the gradient or slope of the energy surface is steepest. The force constants were calculated once.

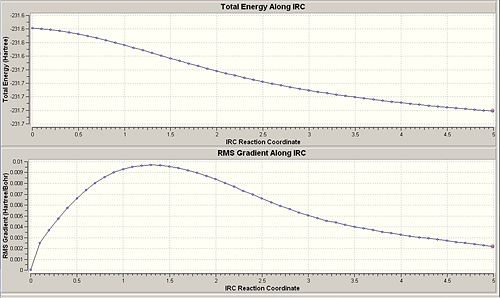
The Chair transition state was taken as a the structure input, and maximum energy along a specified reaction path was found, having also taken into account zero-point energies and so forth. Having produced all of the quantities needed for a variational transition state theory calculation. Initially 50 points were plotted along the IRC to see how the calculation progressed, this can be seen in the IRC graph below; With 50 points the calculation had not reached a minium geometry yet as illustrated in the graphs and images below.

Option two was carried out, the IRC was restarted and 400 points were specified in the hope that this would be enough until the structure optimised to reach a minimum. However, even with 400 points the IRC plotted 94 points and stopped before reaching a minimum as can be seen below and the geometry was not fully optimised,

Therefore method(III) was carried out with the specification to compute force constants (always) at each of the 400 points; However this calculation was very lengthy and failed on two occasions.

IRC, 50 points	IRC, 400 points

In order to calculate the activation energies for the reaction via both transition structures. The cair and boat transition structures were both reoptimised using the B3LYP/6-31G* level of theory and frequency calculations were carried out.

Below the energies of the two geometries were compared between the reactants and transition states at the two levels of theory; What was found is that the geometries are reasonably similar, but the energy differences are markedly different.

Summary of activation energies (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.70	44.69	31.06	33.17	33.5 ± 0.5
ΔE (Boat)	55.60	54.76	41.96	41.32	44.7 ± 2.0

1 hartree = 627.509 kcal/mol

The experimental activation energies are 33.5 ± 0.5 kcal/mol via the chair transition structure and 44.7 ± 2.0 kcal/mol via the boat transition structure at 0 K. The value computed at 298.15K are closer to experimental values than those computed at 0 K, however the difference in going from HF to B3LYP methods to give very accurate results is very significant in lowering the energies obtained.

The Diels Alder cycloaddition

Butadiene

Using the AM1 semi-empirical molecular orbital method to start with the geometry of cis butadiene was optimized. (symmetric or anti-symmetric) with respect to plane.

First optimised using semi empirical AM1 method;

The HOMO and LUMO of cis butadiene were then plotted and its symmetry was determined; The Point group of butadiene is C2v.


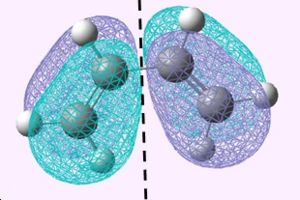LUMO	HOMO

The Lumo is symmetric through the refelection plane illustrated and the Homo is anti-symmetric through the reflection plane illustrated above.

Ethylene and cis butadiene transition structure

For the ethylene and cis butadiene transition structure the transition state was optimised using the ts Berny, semi empirical, AM1 method where force constants were calculated only once, and opt=noeigen was specified under keywords.

The HOMO and LUMO's were plotted, the HOMO is anti-symmetric with respect to a horizontal reflection plane cutting through carbons (2 and3) in the butadiene fragment and the LUMO is symmetric with regards to this reflection plane. This is can be seen below;


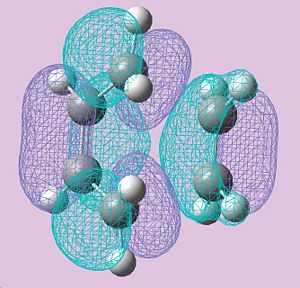LUMO	HOMO

The geometry of the transition structure can be veiwed above, The bond-lengths of the partly formed σ C-C bonds are both 2.20Å .

The typical sp3 and sp2 C-C bondlengths are 1.54Å and 1.33Å respectively, This suggests that the partly formed σ C-C bondlength in the TS is not hybridised and is longer than expected.

The motion of the vibration at -955.01 cm-1 which corresponds to the reaction path at the transition state is illustrated below. The formation of the two bonds is synchronous. This is the opposite for the lowest positive frequency at 268.13 cm-1 which demonstrates an asynchronous motion of bond formation.

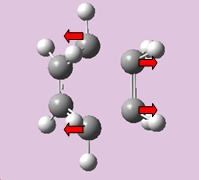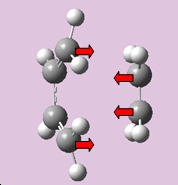The HOMO at the transition structure is anti-symmetric, the HOMO of butadiene which is anti-symmetric and the lumo of ethylene which is alsoanti-symmetric have interacted as they both have the same symmetry properties and significant overlap density which results in an allowed reaction. Where the resultant HOMO with two new σ bonds is antisymmetric as illustrated above.

Cyclohexa-1,3-diene reaction with maleic anhydride

Cyclohexa-1,3-diene undergoes a facile reaction with maleic anhydride to give primarily the endo adduct. The reaction is supposed to be kinetically controlled so that the exo transition state should be higher in energy, The transition states of both the eso and endo form have been optimised using the TS Berny, semi-empirical AM1 methods in order to compare the energies of both forms.

Exo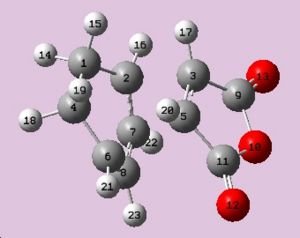

Endo

Pentahelicene

EXO transition state

Pentahelicene

Endo transition state

HOMO EXO

HOMO ENDO

T.S energy -0.05159 a.u

T.S energy -0.05050 a.u

The relative energies of the exo and endo transition structures are: Exo -0.05159 a.u, Endo -0.05050 a.u; this demonstrates that the exo trransition structure is lower in energy therefore the favourable product of kinetic control. The difference between these structural forms is that the maleic anhydride is “opposite” the -CH2-CH2- bond for the exo form and and “opposite” the -CH=CH- bond for the endo). Below are the bond lengths and angles for the regioisomers;

Exo

Endo

Bond type	Exo Bond length (Å)	EndoBond length (Å)
C2-C3	2.16	2.17
C6-C5	2.16	2.17
C3-C5	1.41	1.41
C5-C11	1.49	1.49
C10-C11	1.41	1.41
C9-C10	1.41	1.41
C9-C3	1.49	1.49
C9-C13	1.22	1.22
C7-C8	1.40	1.52
C6-C8	1.39	1.49
C2-C7	1.39	1.49
C1-C4	1.52	1.40

The bond lengths for the regioisomers are very similar they only differ with the differring of carbon number, the delocalised bond lengths are are longer than the normal C-C bond lengths.

The exo form may be more strained as there are steric repulsions of the -CH2-CH2- fragment and the maleic anhydride versus secondary orbital interactions between the π systems of -CH=CH- and -C=O-CO-C=O- fragment which stabilise the endo form.

Overall the endo form is the thermodynamically more stable product due to the additional bonding interaction; From examining the nodal properties of the HOMO between the -C=O-CO-C=O- fragment and the remainder of the system it can be seen that there is a secondary orbital interaction from the C=O groups which interacts with the C=C of the cis butadiene giving rise to better overall orbital overlap. The Exo form is not in the correct orientation and so does not exhibit this.