Rep:Mod:wearethewalri

- Module 3 - Transition states

1: Investigating 1,5-hexadiene

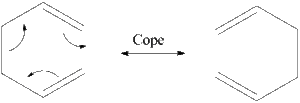
1,5-hexadiene undergoes a textbook [3+3] sigmatropic rearrangement resulting in the concerted breaking of a C-C single bond and formation of a C-C single bond on the other side of the transition state ring . The rearrangement is highly dependent on the starting conformation of the molecule, because the olefins need to be close enough to react. The relative energies of the starting geometries will be investigated, and then the structures of the transition state will be analysed using QST2, IRC several other techniques in order to compare them.

The Anti-periplanar and gauche conformations of 1,5-hexadiene were optimised in gaussian using HF:3-21G method and basis set.

Energies of Anti and Gauche Conformations

Conformation & symmetry	Antiperiplanar2, Ci	Gauche4, C2
Jmol	antiperiplanar	Gauche
Hartree	-231.69253523	-231.69153032
appendix reference	-231.69254	-231.69153
Relative Energy /kjmol	-2.6255	0

the gauche conformation above is not expected to be lower than the anti conformation, as it lacks an important van-der-waals interaction between an alkene hydrogen and a B-alkyl hydrogen, with a internuclear separation of 2.68A corresponding to a strong preference for the anti.

caption

Anti2 showing van-der-waals interaction	Gauche4 with no interaction

The lowest energy conformation should be gauche2, as the gauche system can more effectively involve the alkene hydrogens in van-der-waals interactions with other hydrogens in the molecule by holding the alkene carbons closer together, and allows interaction of the C-H σ bonds with C-Cσ bonds which contribute a larger energy reduction than the C-H->C-H interactions, and also permit better involvement of the π systems. Gauche2 maximises the number of through space interactions.

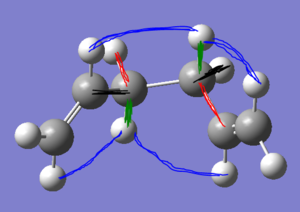
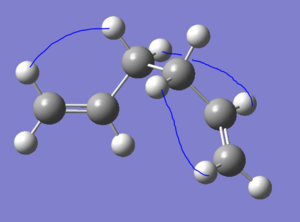
In order to foster the same van-der-waals interactions as in the anti2 conformation it is neccessary to rotate the C-C-C=C dihedral to bring the alkene hydrogens into interacting distance with the alkane hydrogens. the conformation Gauche2 has all of these interactions through space, but isn't the lowest because there is no π-orbital sharing. Gauche3 has the two πsystems closer together, which promotes a spreading of electron density and lowers the energy.

Comparison of HF:3-21g and DFT:B3LYP:6-31G*

caption

	HF:3-21g	DFT:B3LYP:6-31G*
.mol	File:STOWanti2.mol	File:STOWanti2DFT.mol
Hartree	-231.69253523	-234.56807933
Kcal/mol relative	0	-7523.486608

Although the structures look identical, the DFT method and improved basis set have achieved a lower energy than the HF:3-21g method, by a very large relative energy.

Frequency calculation

There were no negative frequencies.

caption

value	/Hartrees	Relative to zero point energy
Sum of Zero point energies	-234.424134	0
sum of thermal energies	-234.418650	14.3982431
sum of thermal enthalpy	-234.417706	16.8767153
sum of thermal free energy	-234.453295	-18.29880768

The zero point energy takes into account the vibrational energy associated with the zero-point vibration, where the quantum number for the vibration is zero, the ground state, but vibrations with associated potential energy are still present .

2: Optimising Chair and Boat structures

The allyl radical was optimised using HF:3-21g to give the C2 symmetric allyl fragment, with the C-C bond length at 1.393A, indicating a partial double bond delocalised over the fragment as expected.

caption

Fragment	HOMO (singly occupied)

Two allyl fragments were aligned to form a transition state guess. One represented the chair structure, one represented the Boat structure. the chair structure was optimised with the berny transition state method, then with the "modRedundant" method to create a reaction profile. the boat form was optimised using the QST2 method.

the chair transition structure

1. Berny Transition state optimisation

The two fragments were positioned as such. The Transition state was found with the berny Transition state setting, giving a frequency for the TS as -817.98cm-1.

caption

Chair guess structure	Transition state vibration
	The Vibration for the transition state

1. REDUNDANT COORDINATE METHOD-

The guess was reopened and edited by setting the two dashed bonds as "bond" then "freeze coordinate" in the Redundant coordinate editor, with the bond length set to 2.2A. the guess was then optimised to a transition state with the berny method using HF:3-21g method and basis set with a frequency calculation. The job terminated with this structure.

then the redundant coordinate bonds were changed from 'freeze coordinate' to 'derivative' and the process was repeated. this yielded the expected transition state, demonstrating the bond electrocyclic reaction as an imaginary vibration of 817.75cm-1. The imaginary frequency shows that the force constant for the vibration is negative: this means that the further the atoms 'vibrate' apart the more force they will be pushed apart with. compare this to a vibration where the atoms experience more force when they are further apart (for a harmonic oscillator).

caption

Transition state structure	Transition state vibration

QST2 method for the Boat transition strucure

In order to find the transition state the QST2 method requires a starting guess and a product guess as inputs. the Method then finds the saddle point in the energy surface between the two structures. This is most effective when the energy surface is simple, for example if the transition state can be reached by movement of only a few atoms. When the two input structures are quite different from each other then there are many possible routes via which the program can attempt to link the two structures, the energy surface is complex, and the output transition structure is likely to be sub-optimal.

when the input guesses were relatively different, the output was not as intended. the energy surface provided a more accessible but not necessarily lower energy saddle point in the form of the chair intermediate.

caption

input/output	QST2 transition state

by modifying the input guesses to be more like the desired transition state it was possible to get the expected answer.

caption

input/output	QST2 transition state
		""-839.98cm-1""

It looks as though the boat transition structure is connecting a structure like Gauche3 or gauche6, and that the chair transition structure resembles structures like gauche2.

IRC method for the chair transition structure

The IRC method takes a transition state as its input and then moves from that point to an optimised minimum. there are multiple possible minima from a particular transition state by definition, so it is important to find all the minima from the transition state and compare the energies. in this case the transition state is between two identical structures, so the question is whether the optimised structure will represent the minimum energy gauche3 conformation found earlier.

Starting with the Chair transition structure the IRC method output 27 steps, arriving at a structure almost identical to the gauche2 conformation.

caption

Starting conformation	animation	final conformation

the Graph of Energy and RMS gradient against reaction coordinate show that the structure did converge to the specified convergence limit, but that the limits needed to be more specific if the structure was to be optimised

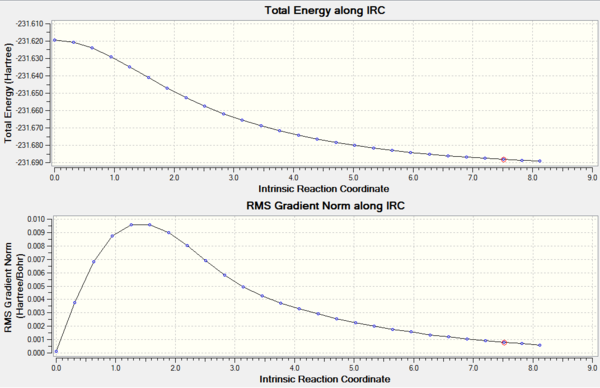
There are three methods to improve the optimisation of the IRC method

1. use more points (takes longer, the optimisation might 'wander' away from the expected structure)
2. calculate the force constants at every step (much more intensive, takes longer, but more accurate)
3. optimise the unfinished output using a normal optimisation (fast, unreliable if the IRC output is too far from a minima)

I did all three, and found that the 'more points' method was unsatisfactory, with the post-optimisation giving the surprise lowest energy of the three. the 'calc force' and more points methods both took around 220 seconds, whilst the post-optimisation was 10x faster.

caption

original IRC output	IRC with 150 steps (3x more)	IRC with force constants every step	Original IRC followed by HF:3-21g opt
	antiperiplanar	antiperiplanar	antiperiplanar
graph:
absolute energy /hartree (-231.61932033)	-231.69166702	-231.69166702	-231.68906248
relative energy /kjmol-1:	-181.33	-188.094	-188.101
Comment:	Poor convergence, see graph	good convergence	good convergence

Relative energies and barriers

The Transition states and reactant structures were optimised at a slightly higher level of theory: B3LYP:6-31g*, so the energies could be compared with the lower level of theory and with experimental values for the kinetic barrier to reaction.

in the calculations both the Chair and boat structures had a tendency to optimise to Gauche2 from the transition states. Whereas comparison here will be done against the anti2 conformation (for easy comparison with the appendix data). This doesn't require anything more complex than simply adjusting the energies, because the relative energies of the conformations have been calculated.

the 0k energy is the 'Electronic + zero point energy' which takes into account the zero-point vibrational energy. For 298k electonic + thermal energy values are used.

caption

structure	Transition state energy (0k,298k)	Barrier height (0k,298k) /kcalmol-1
Chair (HF:3-21g)	-231.467, -231.461	45.682, 44.715
Boat (HF:3-21g)	-231.451, -234.445	55.597, 54.844
Chair (DFT:B3LYP:6-31G*)	-234.415, -234.409	34.073, 33.195
Boat (DFT:B3LYP:6-31G*)	-234.402, -234.396	41.98, 41.352

Experimentally the 0k values for chair are 33.5+/- 0.5 kcal/mol, which compares favourably with the B3LYP calculated energy of 34.073. The boat value of 44.7+/- 2 also compares reasonably well with the calculated 41.98kcal/mol.

3: Diels-Alder Cycloaddition

HF:3-21g calculation was used throughout for speed of calculation. the energies provided are less accurate, although still meaningful.

Cis-butadiene

caption

HOMO	LUMO
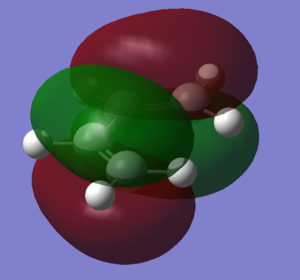antisymmetric	symmetric

transition state geometry for the prototype reaction

the QST2 method was used to find the transition structure. The reactant ethylene was aligned 2.2A above carbons 1 and 4 of the cis-Butadiene, and the product cyclohexene was built and the structure cleaned by gaussian.

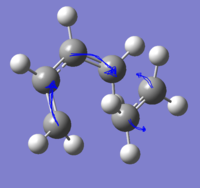
The imaginary vibration corresponding to the transition state, along with the two lowest frequency real vibrations are given below. the transition state frequency corresponds to a concerted bond breaking mechanism, where both σ bonds break/form at the same time. The two lowest energy real vibrations are not symmetric with respect to the plane however. the lowest energy at 166cm-1 is a twisting vibration and doesn't involve much bond stretching, although the vibration at 284cm-1 looks like the asymmetric stretching of the two forming σ-bonds.

caption

-818cm-1	166cm-1	284cm-1

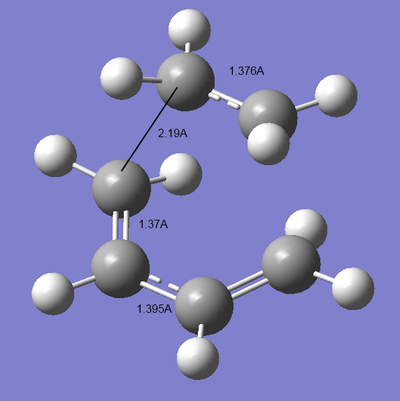
the bond lengths at the transition state show that the ethene carbons are well within the van-der-waals radii of the butadiene carbons, and that the alkenes all have the prototypical <1.4A bond length, whilst the C-C single bond is slightly longer. the long 2.2A bond indicates that this is an early transition state, it resembles the reactant more than the product. there is likely to be a low barrier to activation. [STOWalderIRC.PNG]

caption

Measured bond lengths/A	Sketch of MO interactions

optimal lengths for sp2-sp2 = 1.33A & sp3-sp3 = 1.50A. the lengths measured above indicate that all the C-C bonds have partial double bonding character. the Van-der-waals radius of carbon is 1.7A, so a C-C distance of 2.2A demonstrates good overlap, well within the maximum distance of ~3.4A. The forming C-C σbond length must therefore be due in part to the donation of electrons from the Sp2 bonds, causing them to lengthen.

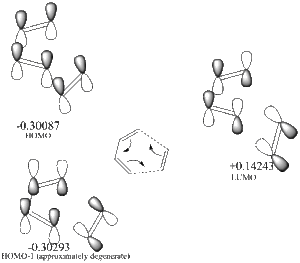
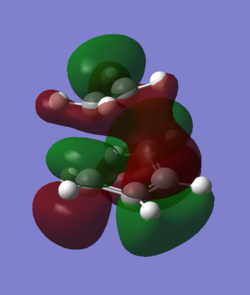
Showing the Interactions for the transition state:

For the transition state:

LUMO	HOMO	HOMO (degenerate)
symmetric anti-bond-forming interaction	symmetric antibonding FMO interaction	antisymmetric bonding interaction between the diene πbonds and the alkene π*

Regioselective Diels-Alder reaction of Maleic anhydride and Cyclohexadiene

QST2 optimisation was used to find the transition structures, which were then optimised with the berny method because the QST2 method had a habit of drawing extra bonds (without affecting the actual structure, purely aesthetic).

the main structural difference between the endo and exo structures is the location of the double bond. the Endo structure has the anhydride moeity over the double bond (hypothetically leading to a favourable electronic interaction) whereas the Exo structure has the anhydride group over the alkyl (leading to increased steric crowding, no favourable electronics).

The calculated energy of a maleic anhydride and a cyclohexadiene (at infinite distance from each other) sum to -605.61063847hartree, so this will be used for comparison. the IRC for both the endo and exo were also calculated.

caption

Product	Transition state	Product	Transition state vibration
ENDO	Endo transition state -605.61036817	Endo transition state -605.72132068	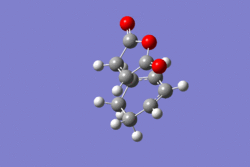-643.69cm-1
EXO	Endo transition state -605.60359118-605.61036817	Endo transition state -605.7187354	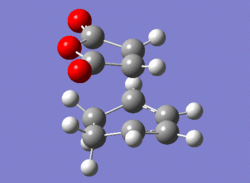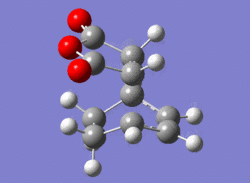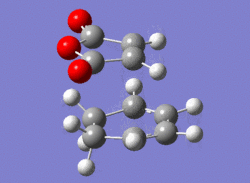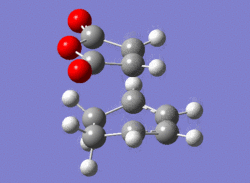-647.49cm-1

IRC calculations were run for both reactions, and plotted on the same graph. The IRC clearly shows that the ENDO reaction has the lower barrier (although it also assigns a lower energy to the Endo product, which is not thought to be correct).

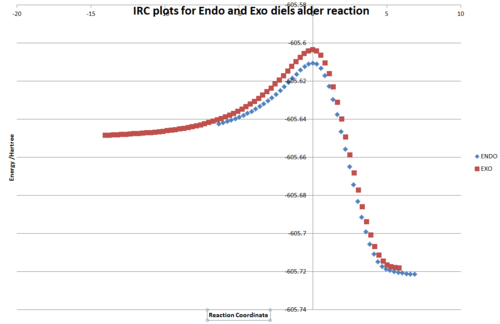
The barrier heights are as below. The barrier height is given "from infinity" (relative to a maleic anhydride and a cyclohexadiene optimised seperately) and "from optimisiation" (which is where the IRC terminated reactant-side). The distinction is important because at infinity there are no interactions between the two reactants. as they come together they reach a minima where there are van-der-waals interactions between the two molecules, before they get closer and repulsive interactions increase up to the transition state. The pre-transition-state minima is at a different energy level for each interaction. if the pre-state is low in energy it will be more populated, but there will be a larger energy barrier for the actual reaction.

Barrier heights (kcal/mol)

Molecule	Barrier height: Infinity	from optimisation
ENDO	0.1696	20.0777
EXO	4.422	28.1716

8kcal/mol is a large difference in energy and easily determines the high selectivity for the reaction. The endo is the kinetic product as there is a greater energy difference from the reactants to the transition state. The Exo product should be lower in energy thermodynamically, although this wasn't observed in these calculations because they were too low a level of theory, and they are similar enough to be considered experimental error here.

The exo transition state and product are more strained due to steric hindrance between the anhydride and the additional alkyl hydrogens, compared to the endo transition state and product, where there is no such steric clash. The endo is favoured in Electronic effects due to several orbital overlap interactions, with the key orbital overlap which can only be present in the Endo transition state involves the central oxygen of the anhydride and the central C-C bond of the diene.

Solvent effects have not been taken into account in these calculations. the solvent has the ability (if polar) to stabilise dipolar transition states, which can make charge buildup more favourable and could disfavour concerted reactions. It can also block sites that might be conferring selectivity or enhance it by increasing steric bulk at functional groups. in this example the anhydride group could be heavily solvated by polar solvents. this would reduce the secondary orbital overlap, but increase the steric interaction with the alkyl hydrogens. This might confer reduced selectivity. Alternatively if the solvent was very non-polar the charged anhydride group might be more likely to reduce its dipole by spreading its electrons with intra-molecular interactions, increasing the Secondary orbital effect and enhancing selectivity The possibility of Higher vibrationally excited populations was also ignored, although at 300K the effect is not large, as excited populations are low.

Orbital Overlap

caption

Cyclohexadiene HOMO	Cyclohexadiene LUMO	Maleic anhydride HOMO	Maleic anhydride LUMO
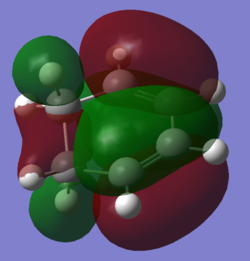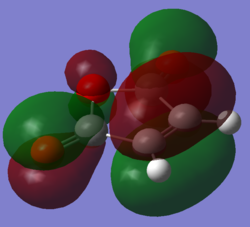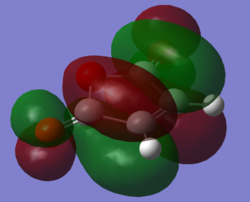antisymmetric	symmetric	symmetric	antisymmetric

Looking at the Reactant orbitals the reaction is permitted by symmetry - there will be good orbital overlap between the π systems. With regards to the regioselectivity, There is one interaction which is noticable quite low in energy in the transition state between the oxygen and the cyclohexadiene forming double bond which constitutes the stabilising endo effect. The carbonyl π bonds do not participate in the Secondary orbital overlap as expected because they are of the wrong phase to interact with orbitals of the cyclohexadiene. Checking the output MOs for the transition state, there are none which involve the C=O orbital fragment directly connected to the alkenes.

caption

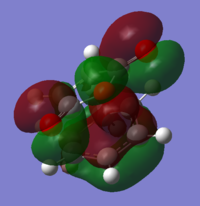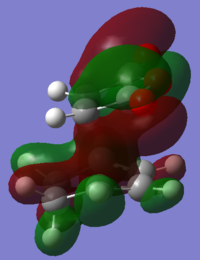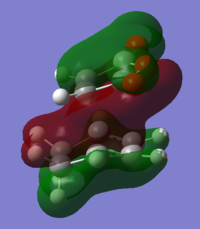oxygen p orbital into diene π system	conjugated C-C=O interacting with diene