Rep:Mod:vs911
Module 3
Cope rearrangemant tutorial
Optimization the reactants and products
(a)Structure of 1,5hexadiene in antiperiplanar confirmation after optimization.
The total energy noted after optimisation is = -231.69260235a.u. After symmetrization, the point group noted is C2.
(b)Structure of 1,5hexadiene in gauche confirmation after optimization.

The total energy noted after optimisation is = -231.69153032a.u. After symmetrization, the point group noted is C2.The energy noted for the gauche conformation was found to be higher than the antiperiplanar confirmation. This is expected as antiperi planar confirmation typically has high stability.
(c)The lowest energy confirmation of 1,5 hexadiene is expected to be the antiperiplanar confirmation.So,another type of the 1,5hexadiene in the antiperiplanar confirmation is drawn and optimised. The structure is as below.
The total energy noted after optimisation is = -231.69253530a.u. This energy is higher than previous antiperiplanar conformer which suggest that the conformer in (a) has the lowest energy.After symmetrization, the point group noted is Ci.
(d)The conformers drawnn in (a),(b),(c) were compared to appendix 1(1).The identification is shown in table below.
| Type | Conformer |
| (a) | anti1 |
| (b) | gauche4 |
| (c) | anti2 |
(e)Ci anti2 conformation of 1,5-hexadiene is located above in (c).Comparison of final energy of this conformer and the one in Appendix 1(1) is tabulated as below.
| Type | Energy |
| (c)-anti2 | -231.69253530a.u |
| appendix 1-anti2 | -231.69254a.u |
This shows that that both energies are very similar and differ only by 0.000005a.u.
(f)Reoptimisation of the structure in (c) is done with B3LYP/6-31G(d)level.The structure of 1,5hexadiene after reoptimization is as below.
The total energy noted after optimisation is = -231.691170279a.u. The structure observed appears to be in antiperiplanar confirmation. Hence, no overall change in geometry is observed.However, significant change in energy between the 2 conformers is observed.The energies differ by 0.003a.u.
(g)Frequency calculation of the structure in (f) is done with B3LYP/6-31G(d)level.The structure of 1,5hexadiene after frequency job is as below.
The frequency calculation allowed all the vibrational frequencies modes to appear,hence, proving it to be real and positive and thus, minimum.The IR spectrum simulated is shown as below.

The log file is opened this time. Hence using the output file,a list of energies under vibrational temperature(thermochemistry) is noted and tabulated as below.
| Type | Energy/a.u |
| Zero-point correction | 0.142491 |
| Thermal correction to Energy | 0.149847 |
| Thermal correction to Enthalpy | 0.150791 |
| Thermal correction to Gibbs Free Energy | 0.110882 |
| Sum of electronic and zero-point Energies | -234.469212 |
| Sum of electronic and thermal Energies | -234.461856 |
| Sum of electronic and thermal Enthalpies | -234.460912 |
| Sum of electronic and thermal Free Energies | -234.500821 |
Optimizing the "Chair" and "Boat" Transition Structures
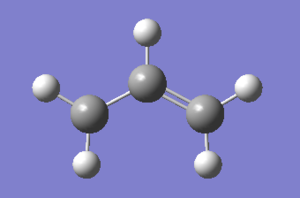
(a)Structure of allyl fragment (CH2CHCH2) which looks like one half of the Transition Structures in Appendix 2(1) after optimization using(HF/3-21G) is as below.
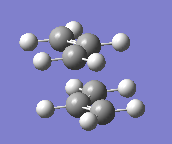
Structure of two allyl fragment,CH2CHCH2 with terminal ends 2.2A apart is as below and an input file of it is saved.
(b)Optimization of this transition state will be done manually in two different ways.First way,
Job type- Opt-freq
Optimization- TS (Berny)
Force constants- Once
Additional keyword box- Opt=NoEigen.
Structure of optimised chair transition state of allyl fragment,CH2CHCH2 using TS(Berny)optimisation is as below
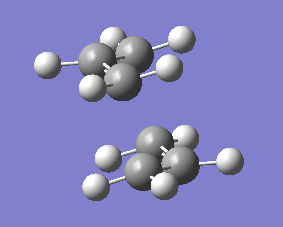
Frequency calculation of the optimised chair transition state is carried out and an imaginery frequency at -817.92 is observed. An animated optimised chair transition state is as below.

(c)Optimization of chair transition state using frozen coordinate method was carried out.This is done firstly using Redundant Coordinate Editor.Secondly, optimization was carried out using the settings below.
Job type- Optimization
Optimization- Minimum
Force constants- Never
Structure of optimised chair transition state of allyl fragment,CH2CHCH2 using frozen bonds optimisation is as below.

(d)Optimized structure looks a lot like the transition optimized in section (b)except the bond forming/breaking distances are fixed to 2.2 Å. Further optimisation was carried out by differentiating the bonds along the way using Redundant Coordinate Editor and using the settings as below.
Job type- Opt-freq
Optimization- TS (Berny)
Force constants- Never
Additional keyword box- Opt=NoEigen.
Final structure of optimised chair transition state of allyl fragment,CH2CHCH2 using Frozen Coordinate Method optimisation is as below.
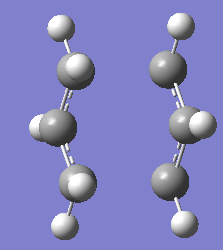
Bond forming/bond breaking bond lengths have been compared to the one optimised using TSBerny optimisation. Both have have the same bond length which is 2.02A.
(e) The boat transition structure will be optimised using the QST2 method. In this method,firstly the numbering of the reactant and product molecule of 1,5hexadiene(anti 2,Ci geometry) was matched with each other.The structure of both reactant and product molecule are as below.
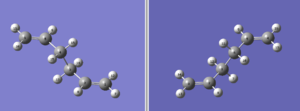
Then,QST2 calculation was performed with the following optimisation settings.
Job type- Opt-freq
Optimization- TS QST2
Force constants- Never
Structure of the failed optimised boat transition structure is as below.
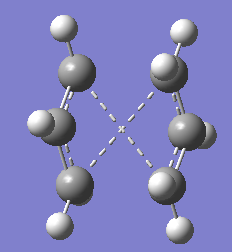
From the above structure,it is observed that it looks a bit like the chair transition structure but more dissociated.The clear cross between the two fragments shows that the optimisation is wrong.This is because the calculation linearly interpolated between the two structures, it simply translated the top allyl fragment and did not even consider the possibility of a rotation around the central bonds.Hence,QST2 method failed.
However,QST2 calculation was performed again after the eactant and product geometries were modified so that they are closer to the boat transition structure.The structure of both reactant and product molecule after modification are as below.
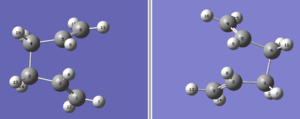
Structure of the successful optimised boat transition structure is as below.
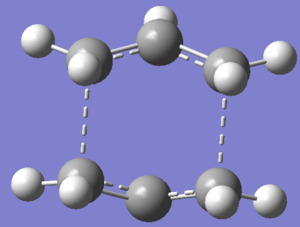
Hence,QST2 method was successful when geometry was modified to resemble transition state of interest.
(f)It is almost impossible to predict which conformer the reaction paths from the transitions structures will lead to.Hence, Intrinsic Reaction Coordinate method was carried out to follow the minimum energy path from a transition structure down to its local minimum on a potential energy surface.The job is carried out with the following job settings.
Job type- IRC
Follow IRC- Forward only
Force constants- Calculate always
Compute more points,N- 50
After calculation, a structure with 44 intermediate geometry is shown.A movie file of these intermediate geometry is shown as below.From the minimum energy of -231.69157740 a.u,the conformer was confirmed to be gauche 4 according to appendix 2

3 approach are suggested to determine the conformer the reaction paths from the transitions structures will lead to. All 3 approach gave a similar conformer although the energy were slightly different
| Aproach | Conformer | Energy/a.u |
| 1 | gauche 2 | -231.69166302 |
| 2 | gauche 4 | -231.69157886 |
| 3 | gauche 4 | -231.69157886 |
This shows that approach 2 and 3 were both reliable. However,if there were to have so many points, it would be unreliable.Hence, approach 3 was accepted to be the best.
(g)The chair and boat transition structures optimised using HF/3-21G level of theory were reoptimised using the B3LYP/6-31G* level of theory.
For the chair transition state, both optimisation was carried out using TSBerny optimisation Structure of the optimised chair transition structure at 2 different level of theory are as below.
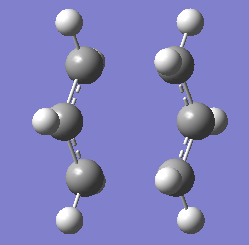 |
 |
| Chair Transition State at HF/3-21G | Chair Transition State at B3LYP/6-31G* |
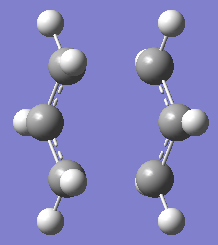
For the chair transition state, HF/3-21G optimisation was carried out using QST2 optimisation but the B3LYP/6-31G* was carried out using TSBerny optimisation.
Structure of the optimised chair transition structure at 2 different level of theory are as below.
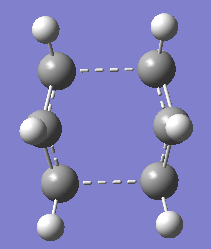 |
 |
|
| Boat Transition State at HF/3-21G | Boat Transition State at B3LYP/6-31G* |
Geometries of each transition state did not change as it got optimised in B3LYP, a higher level of theory.Tabulation of summary of electronic energies of reactant and transition state at different levels of theory are tabulated as below.
| Conformation | HF/3-215 | B3LYP/6-31gd |
| Chair | -231.61932243 | -234.55698303 |
| Boat | -231.60280189 | -234.54309307 |
| 1,5hexadiene(anti2) | --231.69253530 | -234.691170279 |
From the table above,it can be observed that the electronic energy of transition state is indeed higher than the reactant as expected.Between the chair and the boat, chair confirmation is observed to have a lower energy than boat as it is stable with with the confirmation of both transition state lower in the B3LYP when compared to HF/3-21G level of theory. The activation energy at both levels at 0K with comparison to given experimental value were tabulated.
| Conformation | HF/3-215 at 0K | B3LYP/6-31gd at 0K | Experimental value(1) |
| Chair | 45.70 | 34.06 | 33.5 ± 0.5 |
| Boat | 55.60 | 41.96 | 44.7 ± 2.0 |
From the table above, it is observed that the calculate activation energies of transition states are closer to experimental value at B3LYP level as compared to HF/3-21G,a lower level of theory.Activation energy for chair confirmation is seen to be lower than boat as expected as chair is a much stable confirmation and hence, it has a lower level of barrier to overcome in the reaction path
Dies Alder Cycloadditon
In this section, all calculation using AM1 semi-empirical molecular orbital method. 1)A structure of cis-butadiene is drawn in gaussview and optimised to a minimum. Cis structure is particularyly obtained by changing the dihedral angle from 180°-0°.Structure of optimised cis-butadiene is as below.
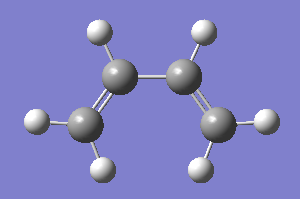
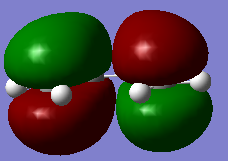
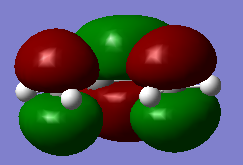
The HOMO and LUMO stuctures of cisbutadiene are plotted as below.
 |
 |
|
| HOMO of cis-butadiene(antisymmteric) | LUMO of cis-butadiene(symmetric) |
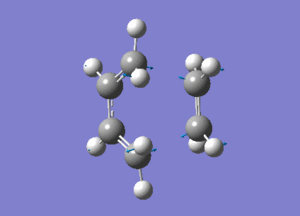
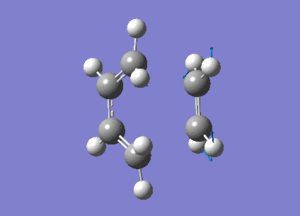
2)Several approaches were taken to locate the optimised ethylene+cis butadiene transition structure. TSBerny method and Frozen coordinate method were sucessful but QST2 method was not.This probably because the position of reactants placed were not similar to the end product.Frequency calculation was performed to characterise transition structure. An imaginery frequency at -954.34 confirmed the formation of the transition structure. Structure of the is as ethylene+cis butadiene transition structure is as below.

The dashed line shown in above image is the partly formed σ C-C bonds in the TS which is found to be 2.12A°.The both bonds form are similar which shows thaye are formen simultaneously(4).Since the geometry of the transition state resemble the reactants, it is called as the early transition state. A typical sp3-sp3 bondlength is 1.54A°(5) and sp2-sp2 bondlength is 1.47A°(5).The Van der waal radii is 1.70A°(5).The bond formed are longer than these typical bond length which confirms that it is the trasnition state and it is just the starting of forming sigma bond.However, it is still shorter than the Vanderwaal diameter due to to intermolecular orbital interaction which leads to further orbital overlap.The vibration which corresponds to the reaction path of the transition state and at lowest positive frequency are shown below.
 |
 |
|
| Vibration at imaginery frequency | Vibration at lowest positive frequency |
From the animation above,it is observed that both bonds indeed form synchronously in the reaction path of the transiton state.This proves that the Dies Alder reaction is indeed a concerted reaction where the bonds form simultaneously.In the vibration at lowest positive frequency,both reactant are vibrating sideways and not towards each other as the vibration at imaginery frequency.Hence, no structural change is expected to be observed due to this vibrational movement.The HOMO and LUMO of both structures are shown as below.
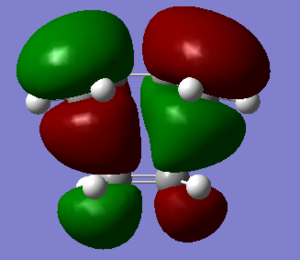 |
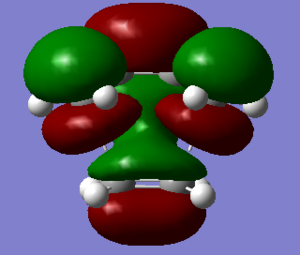 |
|
| HOMO of ethylene+cis-butadiene(symmteric) | LUMO of ethylene+cis-butadiene(antisymmetric) |
For the two compounds to react, a HOMO of one must react with the LUMO of the other with conservation of orbital symmetry. Hence,from looking at the HOMO and LUMO of both reactants using gauss view, it will appropriate for HOMO of cis butadiene react with LUMO of ethylene to form the MO shown above.This is because both of them have the same symmetry which is antisymmeteric(4). Hence, orbital overlap will be in phase. The image shown above proves the significant overlap of orbital to form the MO shown. Hence, the reaction is allowed. Below is a diagram which shows the interaction of HOMO of cis butadiene and LUMO of ethylene.
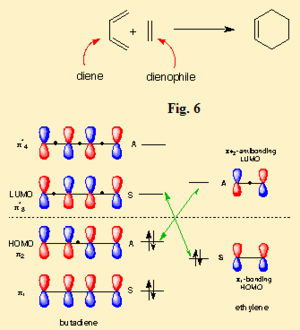
3)Two approaches were taken to locate the optimised cyclohexa-1,3-diene reaction with maleic anhydride transition structure. TSBerny method was not successful and thus , frozen coordinate method was used and was sucessful.TS Berny method failed probably because the overall geometry of transition structure is too complicated.Structure of both endo and exo transition structure of cyclohexa-1,3-diene reaction with maleic anhydride are as below.
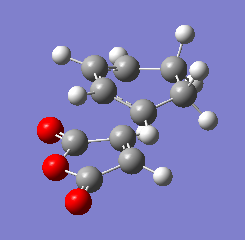 |
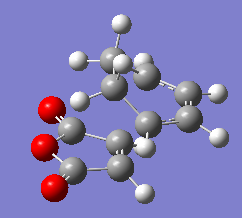 |
|
| Endo form of transition structure | Exo form of transition structure |
The total electronic energies of both endo and exo TS states are tabulated as below.
| Transition States | Energy |
| Endo | -0.05150476a.u |
| Exo | -0.05041980a.u |
The energy difference between the 2 forms of TS are calculated. Energy difference, ΔE = (-0.05041980) - (-0.05150476) = 1.08496*10-3 a.u. = 0.6808 kcal/mol. Energy difference for both form differ only by 0.6808 kcal/mol. However, since endo TS has a lower energy,it is much favourable to form. Structure of both endo and exo transition structure of cyclohexa-1,3-diene reaction with maleic anhydride showing the C-C bond spacing are as below.
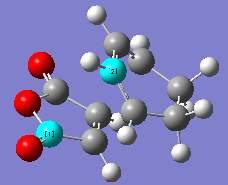 |
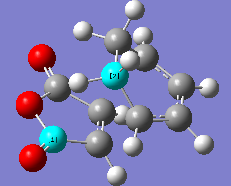 |
|
| Endo form of transition structure | Exo form of transition structure |
The bondlengths for C-C through space is tabulated as below
| Transition States | C-C bond through space |
| Endo | 2.892A° |
| Exo | 2.945A° |
The bond lengths are observed to be longer for exo than endo. This suggest that exo undergoes a leser steric repulsion compared to endo.However, at the same time,secondary orbital interaction can be observed in endo form which pulls the carbonyl groups of the dienophile towards the diene and electron shift from the diene to the dienophile in the TS , making the C-C space shorter than it should be. This is the result of secondary orbital interaction versus steric repulsion(3).
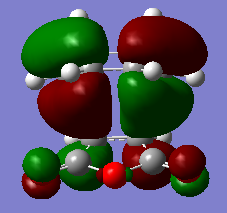
Frequency calculation was performed to characterise transition structure. An imaginery frequency at -806.61 confirmed the formation of the endo transition structure while confirmed the formation of the exo transition structure.Vibration at both imaginery frequency are shown below.
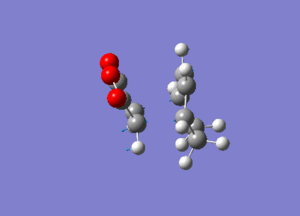 |
 |
|
| Endo form of transition structure | Exo form of transition structure |
The HOMO and LUMO for the endo TS are shown as below.
 |
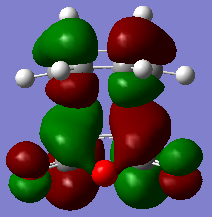 |
|
| HOMO of transition structure | LUMO of transition structure |
The HOMO and LUMO for the exo TS are shown as below.
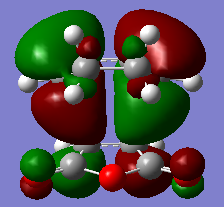 |
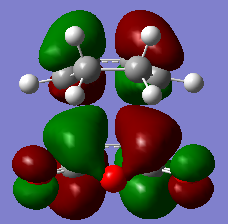 |
|
| HOMO of transition structure | LUMO of transition structure |
From the MO diagrams especially in the HOMO above, it can be clearly be seen that the -(C=O)-O-(C=O)- fragment on the maleic anhydride on the endo form is closer to the other MOs which suggest the existance of secondary orbital overlap which would increases the overlap of the incoming dienophile and the diene. However, in the exo form, the -(C=O)-O-(C=O)- fragment on the maleic anhydride is pointing away from all the other MOs in the structure which suggest almost no interaction such as secondary orbital overlap between the -(C=O)-O-(C=O)- fragment on the maleic anhydride and the other MOs.Hence, this clearly concludes that endoform of TS is definitely more favoured than the exo form.(3)
Further discussion:
Solvent effects are neglected in the calculation although I believe it has minimal effect on the calculation(2).
Reference
1.https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3
2.http://www.ch.ic.ac.uk/ectoc/echet98/pub/064
3.http://pubs.acs.org/doi/abs/10.1021/jo00384a016
4.http://classes.yale.edu/chem220/STUDYAIDS/pericyclic/pericyclic.htm
5.Fox, Marye Anne; Whitesell, James K. (1995). Organische Chemie: Grundlagen, Mechanismen, Bioorganische Anwendungen. Springer. ISBN 978-3-86025-249-9
