Rep:Mod:viktorfrankenstein

Module 2: Bonding analysis using Ab initio and Density functional techniques.

Introduction

The aim of this experiment is to study the use of computational chemistry to analyse molecules that may be difficult to analyse experimentally (due to toxicity, stability etc).

Computational chemistry is already a common tool used to produce all kinds of information regarding a given molecule, for example with computational techniques the dipole moments, predicted IR, bond lengths and angles and many other things can be determined. Those a just a few of the properties this study shall be investigating.

By using the program Gaussview 5.0, in conjuction with Gaussian and a HPC (to compute more complex molecules), all the previously described properties and the MOs and NBOs of given molecules will be determined and compared.

Optimization of different trigonal planar molecules

Optimization of the BH₃ using the B3LYP, 3-21G method

A molecule of BH₃ was created using the program Gaussview 5.0 and then optimized.

The optimization .log file can be found here.

The optimized bond length was found to be: 1.19349 Å

whilst the optimized bond angle was found to be: 120.000°

Summary of BH₃ Optimization (3-21G)
File type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	(3-21G)
Charge	0
Spin	Singlet
Final Energy	-26.46226434 a.u.
Gradient	0.00020672 a.u.
Dipole Moment	0.0000 Debye
Point Group	D3H
Calculation Time	24.0 s

The below data shows how the optimization process has successfully converged. Throughout this study this data will be posted to confirm convergence of each process.

Item               Value     Threshold  Converged?
 Maximum Force            0.000313     0.000450     YES
 RMS     Force            0.000271     0.000300     YES
 Maximum Displacement     0.001610     0.001800     YES
 RMS     Displacement     0.001054     0.001200     YES
 Predicted change in Energy=-1.071764D-06
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  1.1935         -DE/DX =    0.0004              !
 ! R2    R(1,3)                  1.1935         -DE/DX =    0.0004              !
 ! R3    R(1,4)                  1.1935         -DE/DX =    0.0004              !
 ! A1    A(2,1,3)              120.0            -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              120.0            -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              120.0            -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)            180.0            -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

The whole aim of the optimization process is to place the structure in its lowest energy conformatio aka it's equilibrium position. This may be seen on the structures potential energy curve as the point with the most negative energy.

Optimization of the BH₃ using the B3LYP, 6-31G method

A more complex basis set was used in order to obtain a more accurate "picture", however, the more complex the basis set, the longer the computing time of each process.

The optimization .log file can be found here.

The optimized bond length was found to be: 1.19332 Å whilst the optimized bond angle was found to be: 120.000°, which corresponds with literature^[1].

Summary of BH₃ Optimization (6-31G(d,p))
File type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	(6-31G(d,p))
Charge	0
Spin	Singlet
Final Energy	-26.60595934 a.u.
Gradient	0.00000624 a.u.
Dipole Moment	0.0000 Debye
Point Group	D3H
Calculation Time	30.0 s

        Item               Value     Threshold  Converged?
 Maximum Force            0.000433     0.000450     YES
 RMS     Force            0.000284     0.000300     YES
 Maximum Displacement     0.001702     0.001800     YES
 RMS     Displacement     0.001114     0.001200     YES
 Predicted change in Energy=-1.189019D-06
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  1.1914         -DE/DX =    0.0004              !
 ! R2    R(1,3)                  1.1914         -DE/DX =    0.0004              !
 ! R3    R(1,4)                  1.1914         -DE/DX =    0.0004              !
 ! A1    A(2,1,3)              120.0            -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              120.0            -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              120.0            -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)            180.0            -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

TlBr₃ optimization using the B3LYP, Lanl2dz Method

This is a great example of the benefits of using computational chemistry. Tl is a very toxic element, however, by using computational chemistry, chemists can avoid contact/use of Tl.

TlBr₃ was optimized using a medium level basis set, however, since these are large atoms a pseudo-potential was used to help combat relativistic effects not covered by the standard Schrodinger equation.

The link to the D-space containing the optimization can be found here

The optimized bond length was found to be: 2.69000 Å whilst the optimized bond angle was found to be: 120.000°

The literature Tl-Br bond length is found to be 2.512Å [1], which is relatively close to the optimized bond length. It is likely crystal packing forces result in the observed bond length to be smaller than the simulated bond length. The literature bond angle is found to be 120°^[2] aswell.

Summary Table of TlBr₃ Optimization
File type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Final Energy	-91.21750131 a.u.
Gradient	0.00027503 a.u.
Dipole Moment	0.0000 Debye
Point Group	D3H
Calculation Time	28.4 s

        Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000022     0.001800     YES
 RMS     Displacement     0.000014     0.001200     YES
 Predicted change in Energy=-6.084016D-11
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  2.651          -DE/DX =    0.0                 !
 ! R2    R(1,3)                  2.651          -DE/DX =    0.0                 !
 ! R3    R(1,4)                  2.651          -DE/DX =    0.0                 !
 ! A1    A(2,1,3)              120.0            -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              120.0            -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              120.0            -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)            180.0            -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

BBr₃ optimization using the B3LYP, GEN method

The link to the D-space containing the optimization can be found here

The optimized bond length was found to be: 2.02000 Å whilst the optimized bond angle was found to be: 120.000°. Although this bond length does not correspond with the literature bond length of 1.88 Å^[3], crystal packing forces may be the reason why the experimental bond length is much shorter than the optimized length

Summary Table of BBr₃ Optimization
File type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	Gen
Final Energy	-64.42903747 a.u.
Gradient	0.00001412 a.u.
Dipole Moment	0.0000 Debye
Point Group	D3H
Calculation Time	19.2 s

        Item               Value     Threshold  Converged?
 Maximum Force            0.000008     0.000450     YES
 RMS     Force            0.000005     0.000300     YES
 Maximum Displacement     0.000036     0.001800     YES
 RMS     Displacement     0.000023     0.001200     YES
 Predicted change in Energy=-4.027369D-10
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  1.934          -DE/DX =    0.0                 !
 ! R2    R(1,3)                  1.934          -DE/DX =    0.0                 !
 ! R3    R(1,4)                  1.934          -DE/DX =    0.0                 !
 ! A1    A(2,1,3)              120.0            -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              120.0            -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              120.0            -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)            180.0            -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

Comparison of BH₃,TlBr₃ and BBr₃

Bond Distance Comparison
Molecule	Bond Distance (a.u.)
BH₃	1.19349
TlBr₃	2.69000
BBr₃	2.02000

The differences in size and electronegativity, and the extent of orbital overlap, of the atoms in each bond result in the varying bond lengths of different molecules. H and Br are similar in that they can take similar bonding modes and form stable single bonds to centres. Changing ligands can either elongate or contract the bond length. There is a larger difference in Pauling electronegativity between Br (2.74^[4]) and B (2.01^[5]) than H (2.1^[6]) and B, however, it can be seen that the bond length increases as the size of the ligand increases and the ligand is changed from H to Br due to poorer orbital interaction as the valence orbitals on Br are more diffuse than that of H.

Tl and B are both group 13 and thus, have an identical number of valence electrons and can undergo identical bonding arrangements (trigonal planar etc.), however, the Tl-Br bond is found to be longer and weaker than the B-Br bond. This is, once again, due to orbital overlap. Tl is a larger atomic centre than B thus has larger, more diffuse orbitals resulting in poorer overlap and weaker bonds. Furthermore, both Tl and Br are large atoms with large electron clouds, and as a result repulsive Coulombic forces mean that the nuclear centres can not be very close to each other.

Bonding in Gaussview

A bond can be defined as an area where there is a high electron density between two atoms. Bonds are formed when this configuration gives rise to an energy state more stable than if the electrons were not shared and with a single nucleus. It is found that different orbitals (s, p, d, f, g) can interact differently to form bonds of differing shape and size. However, this definition best describes covalent bonding. Different types of bonding e.g ionic and metallic would be described in a different manner. In the cases of the molecules used above, the covalent bond definition best describes them.

Programs like Gaussview define a bond as an area of high shared electron density, thus, as the distance between atoms is increased the the shared electron density falls and the probability of finding an electron in this area falls below a threshold and Gaussview will display the molecule as individual atoms. There may still be interaction/orbital overlap between the two atoms but it is not large enough to be considered influencial. As seen here:

Frequency Analysis

BH₃ Frequency and Vibrational (6-31G(d,p))Analysis

The purpose of frequency analysis is to find the minimum structure on a potential energy surface. It will also produce the frequencies of vibration in spectra which can then be compared to experimental values, allowing conclusions to be drawn after.

Summary of BH₃ Frequency (6-31G(d,p)) Analysis
File type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	(6-31G(d,p))
Charge	0
Spin	Singlet
Final Energy	-26.60595934 a.u.
Gradient	0.00000624 a.u.
Dipole Moment	0.0000 Debye
Point Group	D3H
Calculation Time	11.0 s

After the frequency calculation the molecule is seen to retain it's D3h symmetry. However, a no-symmetry tag was used when conducting the frequency calculation, therefore, in theory the point group symmetry should in fact be CS (no symmetry). It is possible a bug in calculations or an intentional conversion back to default resulted in the point group to be shown as D3h.

The complete frequency analysis can be found here here.

Low frequencies ---  -10.1828   -5.7670   -5.4933   -0.0045    0.0917    1.7554
 Low frequencies --- 1152.4687 1209.4476 1209.4499

                     1                      2                      3
                    A2"                    E'                     E'
 Frequencies --  1152.4687              1209.4476              1209.4499
 Red. masses --     1.2531                 1.1081                 1.1081
 Frc consts  --     0.9806                 0.9550                 0.9550
 IR Inten    --    93.2590                13.2667                13.2698

        Item               Value     Threshold  Converged?
 Maximum Force            0.000012     0.000450     YES
 RMS     Force            0.000006     0.000300     YES
 Maximum Displacement     0.000049     0.001800     YES
 RMS     Displacement     0.000025     0.001200     YES
 Predicted change in Energy=-9.225858D-10
 Optimization completed.
    -- Stationary point found.

The "low frequencies" show the “-6” vibrations of the “3N-6” vibrations of a molecule with N atoms. "Low frequencies" have displacement vectors, which has an observable effect on the molecules centre of mass.

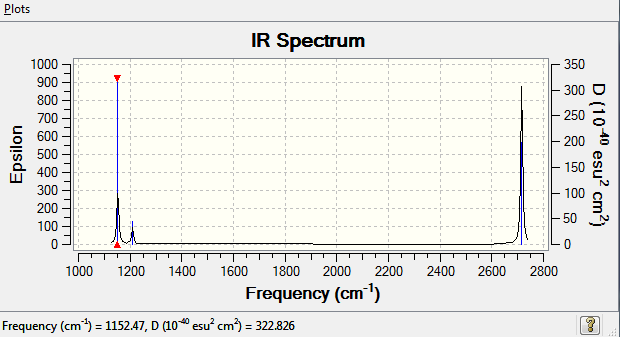
The lowest "real" vibrational mode is found to occur at 1152.4687cm^-1

A summary of the vibrational frequencies of BH₃ is shown in the table below. By re-running a frequency calculation on the molecule, with tight D3h symmetry imposed, vibrations were produced for a defined symmetry group. All vibrations were shown to have a positive minimum energy, confirming the completion of the calculation.

Vibrational Analysis
Mode	Frequency (cm^-1)	Infrared	Description	Symmetry Point Group
1	1152.47	93.2590	Concerted bending of 3 H's in and out of plane with B moving in and out of plane in the opposing direction	A₂"
2	1209.45	13.2667	The 3 H's rocking in-plane	E'
3	1209.45	13.2698	Stationary B atom, whilst 3 H's rock with one of the H's rocking in opposite direction (antisymmetric)	E'
4	2577.47	0.0000	Symmetric stretching of 3 H's	A₁'
5	2715.85	135.5205	Asymmetric stretching of 2 H's whilst 1 proton remains basically stationary	E'
6	2715.85	135.5075	Asymmetric stretching (2 symmetric proton stretches and one in the opposite direction)	E'

Only are seen 3 peaks even though there are 6 vibrational modes because of many reasons. Firstly, vibrational mode 4 will not be seen as it is a completely symmetric stretch and has an infrared intensity of 0. Furthermore, the vibrational modes 2 and 3 are degenerate and so are 5 and 6 meaning they have the same wave number, thus, giving only 3 peaks on an IR spectrum, corresponding to A2" (1152.47cm^-1), E' (1209.45cm^-1) and E' (2715.85cm^-1).

TlBr₃ Frequency and Vibrational (LanL2DZ) Analysis

For comparison purposes, vibrational analysis was carried out on the previously optimized TlBr₃ structure. The Guassian summary can be seen below:

Summary of TlBr₃ Frequency (LanL2DZ) Analysis
File type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	(LanL2DZ)
Charge	0
Spin	Singlet
Final Energy	-91.21750131 a.u.
Gradient	0.00000088 a.u.
Dipole Moment	0.0000 Debye
Point Group	D3H
Calculation Time	19.0 s

 Low frequencies ---   -3.4213   -0.0026   -0.0004    0.0015    3.9367    3.9367
 Low frequencies ---   46.4289   46.4292   52.1449

         Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000022     0.001800     YES
 RMS     Displacement     0.000011     0.001200     YES
 Predicted change in Energy=-5.660901D-11
 Optimization completed.
    -- Stationary point found.

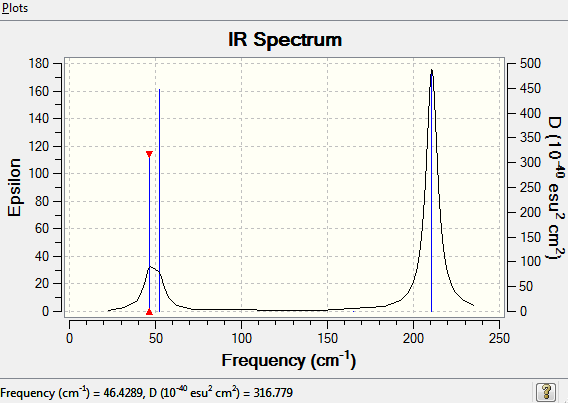
The lowest "real" normal mode is found to occur at 46.4289cm^-1

The complete frequency analysis can be found here

Vibrational Analysis
Mode	Frequency (cm^-1)	Infrared	Description	Symmetry Point Group
1	46.43	3.6867	Scissoring of 2 Br's in plane of molecule (symmetric)	E'
2	46.43	3.6867	The 3 Br's asymmetrically rocking in-plane, 1 Br rocking in the opposing direction to the other two	E'
3	52.14	5.8466	Concerted bending of 3 Br's in and out of plane with B moving in and out of plane in the opposing direction)	A₂'
4	165.27	0.0000	Symmetric stretching of 3 Br's	A₁'
5	210.69	25.4830	Asymmetric stretching of 2 Br's whilst 1 proton remains basically stationary	E'
6	210.69	25.4797	Asymmetric stretching (2 symmetric proton stretches and one in the opposite direction)	E'

Vibrational Frequencies (TlBr₃ vs BH₃)

Vibrational Mode	BH₃ Frequency (cm^-1)	TlBr₃ Frequency (cm^-1)
1	1152.47	46.43
2	1209.45	46.43
3	1209.45	52.14
4	2577.47	165.27
5	2715.85	210.69
6	2715.85	210.69

The following equation for vibrational frequency will be used to compare structures:

ν = \frac{1}{2 π c} \sqrt{\frac{k}{μ}}

where k is the spring constant for the bond, c is the speed of light, and μ is the reduced mass.

It can be seen that the vibrational frequencies for BH₃ are higher than TlBr₃'s. This is because Tl and Br are hearvier atoms than B and H, as a result, the reduced mass of TlBr₃ is larger than the reduced mass of BH₃. From the above equation it can be seen that the vibrational frequency is inversely proportional to the reduced mass, therefore, a larger reduced mass results in a smaller vibrational frequency.

Another reason for the higher frequency is because B and H are smaller nuclei so form stronger bonds. Therefore the K for their bonds should be greater. Resulting in a large vibrational frequency.

Once again only 3 peaks are seen on the IR spectrum for TlBr₃, due to the same reasons discussed earlier.Only are seen 3 peaks even though there are 6 vibrational modes because of many reasons. Firstly, vibrational mode 4 will not be seen as it is a completely symmetric stretch and has an infrared intensity of 0. Furthermore, the vibrational modes 2 and 3 are degenerate and so are 5 and 6 meaning they have the same wave number, thus, giving only 3 peaks on an IR spectrum.

The A2" and E' vibrational modes like close to each other because they are both bending modes whilst the A1' and E vibrational modes lie close to one and other because they are both stretching modes. This is also why A1' and E vibrational modes are higher in energy.

The same method and basis set has to be used for both optimization and frequency analysis calculations because as shown before the total energy is infact dependent on the basis set used and it's accuracy. Therefore, if one were to compare the energies of BH₃ and TlBr₃ directly, the same basis set would have to be used.

Population analysis

Molecular orbitals of BH₃

A complete MO analysis has been published on the D-space and can be found here.

Summary of BH₃ MO Analysis
File type	.log
Calculation Type	SP
Calculation Method	RB3LYP
Basis Set	(6-31G(d,p))
Charge	0
Spin	Singlet
Final Energy	-26.60595934 a.u.
Gradient	0.00000000 a.u.
Dipole Moment	0.0000 Debye
Point Group	D3H
Calculation Time	9.0 s

By linearly combining atomic orbitals (LCAO), the MO diagram below was formed. Computer-generated visualizations of each MO can also be seen beside each theoretical MO:

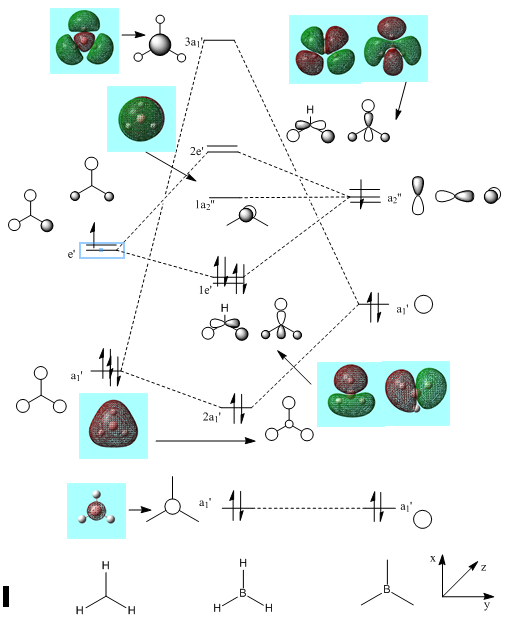
This diagram is proof that MO theory can be an accurate tool to model the molecular frame work of simple molecules. It can be seen on the above diagram that the "real" computer simulated MOs do not differ from the MOs formed from LCAO. However, due to other interactions as the molecule gets more complicated MO theory tends to break down and one must look towards a quantum description.

NH₃ Analysis

Optimization

The log file of the optimization can be found here.

Summary of NH₃ Optimization (6-31G(d,p))
File type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	(6-31G(d,p))
Charge	0
Spin	Singlet
Final Energy	-56.55776856 a.u.
Gradient	0.00000885 a.u.
Dipole Moment	1.8464 Debye
Point Group	C1
Calculation Time	42.0 s

          Item               Value     Threshold  Converged?
 Maximum Force            0.000024     0.000450     YES
 RMS     Force            0.000012     0.000300     YES
 Maximum Displacement     0.000079     0.001800     YES
 RMS     Displacement     0.000053     0.001200     YES
 Predicted change in Energy=-1.629731D-09
 Optimization completed.
    -- Stationary point found.

Frequency Analysis

The log file of the frequency analysis can be found here.

Summary of NH₃ Frequency (6-31G(d,p)) Anaylsis
File type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	(6-31G(d,p))
Charge	0
Spin	Singlet
Final Energy	-56.55776856 a.u.
Gradient	0.00000888 a.u.
Dipole Moment	1.8464 Debye
Point Group	C1
Calculation Time	22.0 s

Low frequencies ---  -30.7764   -0.0013   -0.0013   -0.0005   20.3142   28.2484
 Low frequencies --- 1089.5557 1694.1237 1694.1868

        Item               Value     Threshold  Converged?
 Maximum Force            0.000021     0.000450     YES
 RMS     Force            0.000009     0.000300     YES
 Maximum Displacement     0.000077     0.001800     YES
 RMS     Displacement     0.000039     0.001200     YES
 Predicted change in Energy=-1.603127D-09
 Optimization completed.
    -- Stationary point found.

The lowest "real" normal mode is found to occur at 1089.5557cm^-1

NBO Analysis

A complete MO analysis can be found here.

Summary of NH₃ MO Analysis
File type	.log
Calculation Type	SP
Calculation Method	RB3LYP
Basis Set	(6-31G(d,p))
Charge	0
Spin	Singlet
Final Energy	-56.55776856 a.u.
Gradient	0.00000000 a.u.
Dipole Moment	1.8464 Debye
Point Group	C1
Calculation Time	-

This is the NBO visualization created by Gaussview:

The charge colour range was set to -1.125 and 1.125

Gaussian also found the relative NBO charges on each atom

NBO charge on N: -1.125

NBO charge on H: 0.375

NH₃BH₃ Analysis

Initial Optimization using 3-21G basis set

An initial optimization was done using the 3-21G basis set to allow comparisons between the minimum energies.

The D-space publication of the optimization can be found here.

The structural information uncovered after optimization can be found below:

H-B-H Bond Angle: 113.6 ° to 1 d.p

H-N-H Bond Angle: 109.4° (to 1 d.p)

B-N Bond Length: 1.69 Å (to 3 s.f)

A key observation is that using this basis set Gaussview does not compute the B-N bond length (1.69) as being short enough to be considered a bond.

Summary of NH₃BH₃ Optimization (3-21G)
File type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	(3-21G)
Charge	0
Spin	Singlet
Final Energy	-82.76661837 a.u.
Gradient	0.00003006 a.u.
Dipole Moment	5.8431 Debye
Point Group	C1
Calculation Time	41.7 s

         Item               Value     Threshold  Converged?
 Maximum Force            0.000094     0.000450     YES
 RMS     Force            0.000030     0.000300     YES
 Maximum Displacement     0.000419     0.001800     YES
 RMS     Displacement     0.000178     0.001200     YES
 Predicted change in Energy=-5.742842D-08
 Optimization completed.
    -- Stationary point found.

Optimization using 6-31G (d,p) basis set

The D-space publication of the optimization can be found here.

The structural information uncovered after optimization can be found below:

H-B-H Bond Angle: 113.9 ° to 1 d.p

H-N-H Bond Angle: 107.9° (to 1 d.p)

B-N Bond Length: 1.67 Å (to 3 s.f)

Using this basis set Gaussview computes the presence of a B-N bond

Summary of NH₃BH₃ Optimization (6-31G (d,p))
File type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	(6-31G (d,p))
Charge	0
Spin	Singlet
Final Energy	-83.22469012 a.u.
Gradient	0.00005656 a.u.
Dipole Moment	5.5623 Debye
Point Group	C1
Calculation Time	41.9 s

         Item               Value     Threshold  Converged?
 Maximum Force            0.000132     0.000450     YES
 RMS     Force            0.000037     0.000300     YES
 Maximum Displacement     0.001188     0.001800     YES
 RMS     Displacement     0.000530     0.001200     YES
 Predicted change in Energy=-1.178864D-07
 Optimization completed.
    -- Stationary point found.

Frequency Analysis

The D-Space publication of the frequency analysis can be found here.

Summary of NH₃BH₃ Frequency (6-31G (d,p)) Analysis
File type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	(6-31G (d,p))
Charge	0
Spin	Singlet
Final Energy	-83.22469012 a.u.
Gradient	0.00005649 a.u.
Dipole Moment	5.5623 Debye
Point Group	C1
Calculation Time	49.2 s

Low frequencies ---   -5.0723   -0.0011   -0.0011   -0.0008   16.7996   20.4955
 Low frequencies ---  263.3583  631.3121  638.2345

        Item               Value     Threshold  Converged?
 Maximum Force            0.000254     0.000450     YES
 RMS     Force            0.000056     0.000300     YES
 Maximum Displacement     0.001409     0.001800     YES
 RMS     Displacement     0.000660     0.001200     YES
 Predicted change in Energy=-2.119842D-07
 Optimization completed.
    -- Stationary point found.

The lowest "real" normal mode is found to occur at 263.3583cm^-1

Determining the B-N bond dissociation energy

Using the 6-31G basis set the energies obtained were as follows:

E(NH₃)= -56.55776856 a.u.

E(BH₃)= -26.60595934 a.u.

E(NH₃BH₃)= -83.22469012 a.u.

The difference in energy between the energy of an NH₃BH₃ and the sum of the energies of its components (NH₃ and BH₃) is the bond dissociation energy, therefore, the following equation can be used

ΔE = E(NH₃BH₃) - (E(NH₃) + E(BH₃))

ΔE = (-83.22469012)-((-56.55776856)+(-26.60595934))

ΔE = -0.06096222 a.u.

E_dissoc = -159.9 kJ/mol-1 (to 4 s.f)

The experimental dissociation energy is found to be a bit higher, -172.1 kJ mol^-1^[7].

Investigating Aromaticity

In this mini project, benzene and it's isoelectronic (42 e^-) analogues will be analysed. The charge distribution and MOs of each structure will be investigated.

Benzene Analysis

The higher level basis set (6-31G (d,p)) was used with the DFT method and the B3LYP hybrid functional used in previous optimizations. A "symmetrise" function in Gaussview was applied during the optimization calculation set up. This was to ensure that the correct symmetry (D_6h, in the case of benzene) is obtained. If this function is not employed the structure obtained is of incorrect symmetry (C₁)

Optimization

Using a 6-31G(d,p) basis set the structure of benzene was optimized. The D-space publication of the optimization can be found here

Benzene

File Type	.log
Calculation Type	FOPT
Calculation Method	RB3YLP
Basis Set	6-31G(d,p)
Final Energy	-232.25821186 a.u.
Gradient	0.00009338 a.u.
Dipole Moment	0.00 Debye
Point Group	D_6h
Calculation Time	1 minutes 14.7 seconds
C-C Bond Length	1.40 Å (to 3 s.f)
C-H Bond Length	1.086 Å (to 4 s.f)
H-C-C Bond Angle	120.0 (to 4 s.f)

The optimized C-C bond length was found to correspond with the literature value of 1.40Å^[8]

         Item               Value     Threshold  Converged?
 Maximum Force            0.000204     0.000450     YES
 RMS     Force            0.000084     0.000300     YES
 Maximum Displacement     0.000870     0.001800     YES
 RMS     Displacement     0.000313     0.001200     YES
 Predicted change in Energy=-4.983462D-07
 Optimization completed.
    -- Stationary point found.

Frequency Analysis

The D-Space publication of the frequency analysis can be found here.

Summary of Benzene Frequency Analysis (6-31G (d,p))
File type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	(6-31G (d,p))
Charge	0
Spin	Singlet
Final Energy	-232.25821186 a.u.
Gradient	0.00009337 a.u.
Dipole Moment	0.00 Debye
Point Group	D_6h
Calculation Time	4 minutes 14.2 s

         Item               Value     Threshold  Converged?
 Maximum Force            0.000202     0.000450     YES
 RMS     Force            0.000093     0.000300     YES
 Maximum Displacement     0.000833     0.001800     YES
 RMS     Displacement     0.000367     0.001200     YES
 Predicted change in Energy=-4.850175D-07
 Optimization completed.
    -- Stationary point found.

Low frequencies ---  -14.2161   -2.6991   -0.0006   -0.0001    0.0003   10.0048
 Low frequencies ---  413.7277  414.5534  621.0444

The lowest "real" normal mode is found to occur at 413.7277cm^-1

NBO Analysis

A complete MO analysis can be found here.

This is the NBO visualization created by Gaussview:

The charge colour range was set to -0.239 and 0.239

Gaussian also found the relative NBO charges on each atom

NBO charge on C: -0.239

NBO charge on H: 0.239

The uniform charge distribution in benzene emphasizes the symmetry of the molecule. All C's carry an electro-negative, -0.239, charge whilst all 6 H's carry an electro-positive, 0.239, charge.

The Molecular Orbital Diagram of Benzene

By using the LCAO method previously used on the BH₃ structure and the addition of the computer simulated molecular orbitals produced by Gaussview, the MO diagram for benzene was made on ChemDraw.

The first six MOs are considered "core" MOs and involve the 2s orbitals of the carbon atmons. These orbitals do not have much effect over the stability of the whole molecule. Therefore, the following MO diagram involves the 7th MO and onwards up to the degenerate LUMOs.

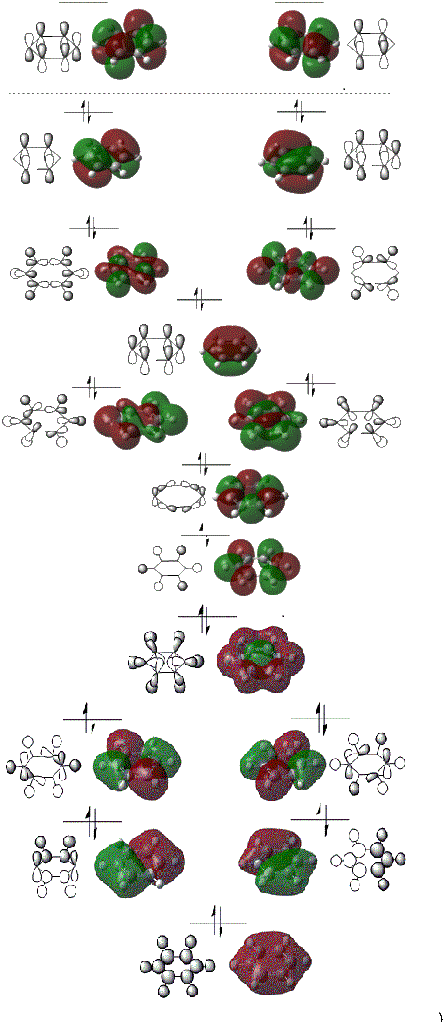
In the above figure we can clearly see the HOMO and LUMO orbitals.

From the above MO diagram it is clear to see that the pi cloud from the pi bonding MO's cover both faces of the entire benzene ring. This suggests that there is indeed delocalisation of the pi electrons across the ring. From the shape of the above MO's it is clear to see that the probability of finding an electron in the pi electron cloud is the same. However, the the overlap of the ring's p orbitals does not reach the molecule's centre. Therefore, it can be seen that the probability of finding an electron in the centre of the ring is 0 as seen from the lack of electron density in the ring's centre.

Boratabenzene Analysis

Boratabenzene is an isoelectronic analogue to benzene where one C-H unit is replaced with a B-H. It also has a -1 charge in order to be isoelectronic.

Optimization

Using a 6-31G(d,p) basis set the structure of Boratabenzene was optimized. The D-space publication of the optimization can be found here.

Boratabenzene

File Type	.log
Calculation Type	FOPT
Calculation Method	RB3YLP
Basis Set	6-31G(d,p)
Final Energy	--219.02052984 a.u.
Gradient	0.00015840 a.u.
Dipole Moment	2.8465 Debye
Point Group	C_2v
Calculation Time	3 minutes 59.6 seconds
(α)C –(β)C and (β)C –(γ)C Bond Length	1.40 Å (to 3 s.f)
B-H Bond Length	1.219 Å (to 4 s.f)
C-H Bond Length	1.092 Å (to 4 s.f)
H-B-C Bond Angle	122.4 (to 4 s.f)
H-C-C Bond Angle	119.8 (to 4 s.f)

The optimized bond lengths were found to correspond with the literature^[9].

         Item               Value     Threshold  Converged?
 Maximum Force            0.000159     0.000450     YES
 RMS     Force            0.000069     0.000300     YES
 Maximum Displacement     0.000878     0.001800     YES
 RMS     Displacement     0.000326     0.001200     YES
 Predicted change in Energy=-6.589451D-07
 Optimization completed.
    -- Stationary point found.

Frequency Analysis

The D-Space publication of the frequency analysis can be found here.

Summary of Boratabenzene Frequency Analysis (6-31G (d,p))
File type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	(6-31G (d,p))
Charge	-1
Spin	Singlet
Final Energy	-219.02052984 a.u.
Gradient	0.00015838 a.u.
Dipole Moment	8.9433 Debye
Point Group	C_2v
Calculation Time	5 minutes 33.2 s

          Item               Value     Threshold  Converged?
 Maximum Force            0.000434     0.000450     YES
 RMS     Force            0.000158     0.000300     YES
 Maximum Displacement     0.000887     0.001800     YES
 RMS     Displacement     0.000394     0.001200     YES
 Predicted change in Energy=-7.191454D-07
 Optimization completed.
    -- Stationary point found.

Low frequencies ---  -13.1275    0.0008    0.0009    0.0011   15.0447   18.1653
 Low frequencies ---  371.3454  404.2334  565.2534

The lowest "real" normal mode is found to occur at 371.3454cm^-1

NBO Analysis

A complete MO analysis can be found here.

This is the NBO visualization created by Gaussview:

The charge colour range was set to -0.588 and 0.588

Gaussian also found the relative NBO charges on each atom.

Since Boratabenzene is not as symmetrical as Benzene, thus there is an uneven charge distribution. Boron is electro-positive in comparison to carbon and hydrogen so has a more positive value than it's adjacent Cs and H. The C para to the B also has an increased negative charged compared to neighboring carbons. This may be do to an "across ring" inductive effect.

Pyridinium Analysis

Pyridinium is an isoelectronic analogue to benzene where one C-H unit is replaced with an N-H. It also has a +1 charge in order to be isoelectronic.

Optimization

Using a 6-31G(d,p) basis set the structure of Pyridinium was optimized. The D-space publication of the optimization can be found here

Pyridinium

File Type	.log
Calculation Type	FOPT
Calculation Method	RB3YLP
Basis Set	6-31G(d,p)
Final Energy	-248.66807396 a.u.
Gradient	0.00003911 a.u.
Dipole Moment	1.8727 Debye
Point Group	C_2v
Calculation Time	4 minutes 16.0 seconds
(α)C –(β)C Bond Length	1.38 Å (to 3 s.f)
(β)C –(γ)C Bond Length	1.40 Å (to 3 s.f)
N-H Bond Length	1.017 Å (to 4 s.f)
C-H Bond Length	1.084 Å (to 4 s.f)
H-N-C Bond Angle	118.3 (to 4 s.f)
H-C-C Bond Angle	121.5 (to 4 s.f)

The optimized bond lengths were found to correspond with the literature^[10].

          Item               Value     Threshold  Converged?
 Maximum Force            0.000064     0.000450     YES
 RMS     Force            0.000023     0.000300     YES
 Maximum Displacement     0.000822     0.001800     YES
 RMS     Displacement     0.000175     0.001200     YES
 Predicted change in Energy=-6.915416D-08
 Optimization completed.
    -- Stationary point found.

Frequency Analysis

The D-Space publication of the frequency analysis can be found here.

Summary of Pyridinium Frequency Analysis (6-31G (d,p))
File type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	(6-31G (d,p))
Charge	1
Spin	Singlet
Final Energy	-248.66807396 a.u.
Gradient	0.00003919 a.u.
Dipole Moment	1.8727 Debye
Point Group	C_2v
Calculation Time	4 minutes 18.1 s

         Item               Value     Threshold  Converged?
 Maximum Force            0.000155     0.000450     YES
 RMS     Force            0.000039     0.000300     YES
 Maximum Displacement     0.000776     0.001800     YES
 RMS     Displacement     0.000228     0.001200     YES
 Predicted change in Energy=-7.473754D-08
 Optimization completed.
    -- Stationary point found.

 Low frequencies ---   -7.2125   -0.0009    0.0004    0.0005   17.3350   18.5324
 Low frequencies ---  392.4554  404.0615  620.4713

The lowest "real" normal mode is found to occur at 392.4554cm^-1

NBO Analysis

A complete MO analysis can be found here.

This is the NBO visualization created by Gaussview:

The charge colour range was set to -0.483 and 0.483

Gaussian also found the relative NBO charges on each atom.

Pyridinium is also not as symmetrical as Benzene, thus there is an uneven charge distribution. N is more electron withdrawing than carbon and hydrogen so has a more negative value than the Cs and Hs in the structure. H is less electro-negative than N and C thus all the protons have positive charge densities with the proton bound to the N having the most positive charge.

Borazine Analysis

Borazine is an isoelectronic analogue to benzene where the C-H units are replaced with alternating B-H and N-H unites. It is a neutral molecule.

Optimization

Using a 6-31G(d,p) basis set the structure of Borazine was optimized. The D-space publication of the optimization can be found here

Borazine

File Type	.log
Calculation Type	FOPT
Calculation Method	RB3YLP
Basis Set	6-31G(d,p)
Final Energy	--242.68459819 a.u.
Gradient	0.00006417 a.u.
Dipole Moment	0.00 Debye
Point Group	D_3h
Calculation Time	4 minutes 56.6 seconds
B-N Bond Length	1.43 Å (to 3 s.f)
B-H Bond Length	1.194 Å (to 4 s.f)
N-H Bond Length	1.010 Å (to 4 s.f)
H-B-N Bond Angle	121.4 (to 4 s.f)
H-N-B Bond Angle	118.6 (to 4 s.f)

The optimized B-N bond length was found to correspond with the literature^[11].

         Item               Value     Threshold  Converged?
 Maximum Force            0.000086     0.000450     YES
 RMS     Force            0.000033     0.000300     YES
 Maximum Displacement     0.000252     0.001800     YES
 RMS     Displacement     0.000077     0.001200     YES
 Predicted change in Energy=-9.332344D-08
 Optimization completed.
    -- Stationary point found.

Frequency Analysis

The D-Space publication of the frequency analysis can be found here.

Summary of Borazine Frequency Analysis (6-31G (d,p))
File type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	(6-31G (d,p))
Charge	0
Spin	Singlet
Final Energy	-242.68459819 a.u.
Gradient	0.00006405 a.u.
Dipole Moment	0.00 Debye
Point Group	D_3h
Calculation Time	4 minutes 14.2 s

 
         Item               Value     Threshold  Converged?
 Maximum Force            0.000201     0.000450     YES
 RMS     Force            0.000064     0.000300     YES
 Maximum Displacement     0.000310     0.001800     YES
 RMS     Displacement     0.000105     0.001200     YES
 Predicted change in Energy=-1.072473D-07
 Optimization completed.
    -- Stationary point found.

Low frequencies ---   -7.1006    0.0005    0.0006    0.0007    7.3495   13.0341
 Low frequencies ---  288.5926  290.5612  404.23114

The lowest "real" normal mode is found to occur at 288.5926cm^-1

NBO Analysis

A complete MO analysis can be found here.

This is the NBO visualization created by Gaussview:

The charge colour range was set to -1.102 and 1.102

Gaussian also found the relative NBO charges on each atom.

There is some symmetry in the charge distribution in Borazine but the difference in electro-negativity of B and N leads to a higher difference in charge for the adjacent atoms compared to Boratabenzene and Pyridinium. This difference also results in the protons bound to B having a more negative charge than protons bound to N.

Comparison of Isoelectronic aromatic 6-membered rings

Charge Distrbution

Charge Distribution
Benzene	Boratabenzene	Pyridinium	Borazine

Benzene has a uniform charge density due to it's symmetry. All protons have identical relative charges, as do all carbons. Borazine is also quite symmetrical so all the N's have the same charge density and all the B's have identical charge densities, however, the electro-positive nature of B and the electro-negative nature of N mean that protons attached to N have more positive charge than protons attached to B.

The extra negative charge in Boratabenzene and the electropositive nature of boron result in the Cs to be more charged than the Cs in Benzene. Furthermore, the carbons nearest to the boron have more electron density localised around them than further carbons, this also holds true for the H directly bonded to B.

In contrast, the extra positive charge in Pyridinium and the electron-withdrawing nature of N, result in some of the Cs to be more positively charged than in benzene. The carbons adjacent to the N are more positive than the others, this is also true for the proton bound directly to the N. A strange observation is that the C para to the N in Pyridinium has a more positive than it's adjacent carbon's. This suggests the possibility of "across ring" electron withdrawal.

Discussion of Molecular Orbitals and MO Diagrams for isoelectronic structures

π1 Orbitals
Type	Benzene	Boratabenzene	Pyridinium	Borazine
MO
LCAO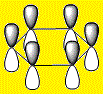

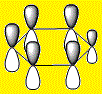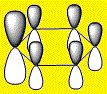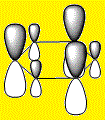From the above images it's clear to see that all 4 molecules have a delocalised electron cloud on both faces of the ring, resulting in the aromatic nature of each molecule. However, there is also a noticeable difference in the distribution of the electron density across each face, which can be rationalized by observing the relative eletro-negativity of each atom.

The electron distribution is uniform in the case of the highly symmetrical benzene, however as the C-H unit is replaced with a different substituent, distortions begin to appear.

The electro-negative N pulls the electron density close to itself which results in the distorted shapes found in Pyridinium, inversely, the electropositive B has electron density pulled away from it resulting in the carbons in Boratabenzene to have a majority of the electron density. The symmetrical nature of Borazine results in a relatively uniform electron density distribution.

In an MO diagram, the electro-negative nature of N in Pyridinium causes a lowering in the energy of the all the MO's it interacts with, as it stablises them by causing a contraction in orbital size. As a result, Pyridinium would have the lowest energy orbitals. On the other hand, the electro-positive B causes a rise in the energy of MO's, therefore, Boratabenzene would have the highest energy orbitals. Although, Borazine has 3 B atoms and 3 N atoms in terms of overall electro-negativity/electro-positivity, Pyridinium is still more electro-negative and Boratabenzene is more electro-positive.

On a relative scale Pyridinium would have the lowest energy orbitals, with Benzene and Borazine as intermediates, whilst Boratabenzene would have the highest energy orbitals.

Another thing to note, is that in terms of degeneracy, due to lack of symmetry caused by the presence of hetero-atoms in Pyridinium and Boratabenzene (both are C_2v), the MO's of these structures will not have as many degenerate orbitals in comparison to the other two structures. Furthermore, since Benzene is more symmetric than Borazine (D_6h vs D_3h), Benzene will have more degenerate MO's than Borazine.

HOMO Orbitals (Orbital 21)
Type	Benzene	Boratabenzene	Pyridinium	Borazine
MO
LCAO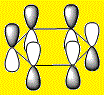

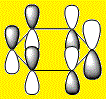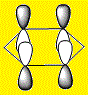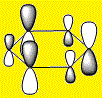The HOMOs and HOMO-1s (orbital 20) are π type orbitals and as mentioned before, the symmetry in Benzene and Borazine result in degenerate HOMOs while the presence of a hetero-atom in boratabenzene and pyridinium removes degeneracy result in them only having a single HOMO. Each HOMO has 1 nodal plane.

Orbital 20
Type	Benzene	Boratabenzene	Pyridinium	Borazine
MO
LCAO

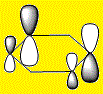The charge distribution in the HOMO's is explained using the same theory discussed with the totally bonding π orbitals.

Using the Benzene LCAO's from the above tables it is easy to see why it is easier to construct an MO for Benzene than the other structures. Benzene is a homogeneous molecule in the sense that all the AO's in a combination are the same size. Therefore, it's electron distribution would indeed be uniform. The LCAO's also effectively display the effect of electro-negativity on charge distribution, the electro-negative N atom has a larger P orbital, so has more electron density and the electro-positive B atom has a smaller P orbital, thus has less electron density surrounding it.

Orbital Energies *(to 2 d.p)*
MO	Benzene	Boratabenzene	Pyridinium	Borazine
π1 Orbitals	-0.36	-0.13	-0.64	-0.36
HOMO	-0.25 (doubly degenerate)	+0.01	-0.48	-0.28 (doubly degenerate)
HOMO-1	-0.25 (doubly degenerate)	-0.03	-0.52	-0.28 (doubly degenerate)

For further justification that Pyridinium would have the lowest energy orbitals, with Benzene and Borazine as intermediates, whilst Boratabenzene would have the highest energy orbitals. One can look at the orbital energies and see that Pyridinium indeed has the lowest (most negativie) energy from stabilisation and Boratabenzene has the highest (most positive) energy out of the 4 structures.

Conclusions

After completing this project it is easy to understand how computational chemistry is a necessity in modern chemistry. With it we can optimize and model any molecule of our choosing, regardless of it's size or complexity. It allows chemists to understand even the most toxic of chemicals, without ever having to touch them. With the simulated data one can predict reaction pathways of molecules and also compare molecules (isoelectronic, isostructural etc) and understand their characteristics.

References

<references> ^[7]

↑ M. Schuurman, W. Allen, H. Schaefer, Journal of Computational Chemistry, 2005, 26, 1106
↑ M. Anatosov et al., J. Phys. Chem. , 105, 2001, pp 5450 - 5467
↑ C. Ballhausen, H. Gray, Inorg. Chem. , 1 (1), 1962, pp 111-122
↑ L. Pauling, J. Chem. Soc. A. , 69, 1947, pp 542
↑ L. Pauling, J. Chem. Soc. A. , 69, 1947, pp 542
↑ L. Pauling, J. Chem. Soc. A. , 69, 1947, pp 542
↑ ^7.0 ^7.1 Yu. Kh. Shaulov; G. O. Shmyreva; V. S. Tubyanskaya, Zhurnal Fizicheskoi Khimii, 1966, 40,122-124
↑ H. Burgi et al., Angewandte Chemie, 34(13), 1995, pp 1454-1456
↑ R. Minyaev et al., Russ. Chem. Bull., Int. Ed. , 50(12), 2001, pp 2332
↑ P. Eaton et al., J.Am.Chem.Soc., 86(15), 1964, pp 3157-3158
↑ W. Harshbarger et al., Inorg. Chem., 8(8), 1969, pp 1683-1689

[1] M. Schuurman, W. Allen, H. Schaefer, Journal of Computational Chemistry, 2005, 26, 1106

[2] M. Anatosov et al., J. Phys. Chem. , 105, 2001, pp 5450 - 5467

[3] C. Ballhausen, H. Gray, Inorg. Chem. , 1 (1), 1962, pp 111-122

[4] L. Pauling, J. Chem. Soc. A. , 69, 1947, pp 542

[5] L. Pauling, J. Chem. Soc. A. , 69, 1947, pp 542

[6] L. Pauling, J. Chem. Soc. A. , 69, 1947, pp 542

[Shaulov-7] 7.0 ^7.1 Yu. Kh. Shaulov; G. O. Shmyreva; V. S. Tubyanskaya, Zhurnal Fizicheskoi Khimii, 1966, 40,122-124

[8] H. Burgi et al., Angewandte Chemie, 34(13), 1995, pp 1454-1456

[9] R. Minyaev et al., Russ. Chem. Bull., Int. Ed. , 50(12), 2001, pp 2332

[10] P. Eaton et al., J.Am.Chem.Soc., 86(15), 1964, pp 3157-3158

[11] W. Harshbarger et al., Inorg. Chem., 8(8), 1969, pp 1683-1689

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

Module 2: Bonding analysis using Ab initio and Density functional techniques.

Introduction

Optimization of different trigonal planar molecules

Optimization of the BH3 using the B3LYP, 3-21G method

Optimization of the BH3 using the B3LYP, 6-31G method

TlBr3 optimization using the B3LYP, Lanl2dz Method

BBr3 optimization using the B3LYP, GEN method

Comparison of BH3,TlBr3 and BBr3

Bonding in Gaussview

Frequency Analysis

BH3 Frequency and Vibrational (6-31G(d,p))Analysis

TlBr3 Frequency and Vibrational (LanL2DZ) Analysis

Vibrational Frequencies (TlBr3 vs BH3)

Population analysis

Molecular orbitals of BH3

NH3 Analysis

Optimization

Frequency Analysis

NBO Analysis

NH3BH3 Analysis

Initial Optimization using 3-21G basis set

Optimization using 6-31G (d,p) basis set

Frequency Analysis

Determining the B-N bond dissociation energy

Investigating Aromaticity

Benzene Analysis

Optimization

Frequency Analysis

NBO Analysis

The Molecular Orbital Diagram of Benzene

Boratabenzene Analysis

Optimization

Frequency Analysis

NBO Analysis

Pyridinium Analysis

Optimization

Frequency Analysis

NBO Analysis

Borazine Analysis

Optimization

Frequency Analysis

NBO Analysis

Comparison of Isoelectronic aromatic 6-membered rings

Charge Distrbution

Discussion of Molecular Orbitals and MO Diagrams for isoelectronic structures

Conclusions

References

Optimization of the BH₃ using the B3LYP, 3-21G method

Optimization of the BH₃ using the B3LYP, 6-31G method

TlBr₃ optimization using the B3LYP, Lanl2dz Method

BBr₃ optimization using the B3LYP, GEN method

Comparison of BH₃,TlBr₃ and BBr₃

BH₃ Frequency and Vibrational (6-31G(d,p))Analysis

TlBr₃ Frequency and Vibrational (LanL2DZ) Analysis

Vibrational Frequencies (TlBr₃ vs BH₃)

Molecular orbitals of BH₃

NH₃ Analysis

NH₃BH₃ Analysis