Rep:Mod:victoriasponge8

Contained within these wiki pages is the report by Martin Champion (mjc07) for the Third Year Organic Computational Project, Department of Chemistry, Imperial College London (March 2010).

The aim of this report is to show the findings of molecular mechanics and semi-empriacal molecular orbital theory calculations on organic systems used in such a way to predict the properties of isomers and the products of reactions. All molecular 3D models unless stated otherwise were drawn in ChemBio3D Ultra 2010 Ver: 12.0. MM2 and MMFF94 molecular mechanics calculations were used from the interfaces within ChemBio3D with no parameters changed unless otherwise stated. Semi-empirical molecular orbital calculations were initially performed in ChemBio3D using the MOPAC interface and the AM1 and PM6 methods.Later calculations were performed using Gaussian 09 on the departmental scan cluster and the results (IR, NMR) viewed from GaussView 5. (Included which calculations were performed on gaussian).

Molecular mechanics modelling of Organic systems

The first part of this project looks how using molecular mechanics approaches (bond lengths and angles) can be used to reasonably approximate real systems and thus how reactivity properties of a molecule(reaction) can be predicted by comparing different geometries of molecules and there isomers.

Hydrogenation of the Cyclopentadiene dimer

Fig 1: Possible products of dimerisation

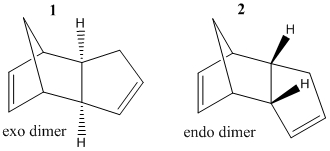
Cyclopentadiene, a useful precursor in organic and especially organometallic synthesis, dimerises spontaneously via a _π4_s + _π2_s cycloaddition at room temperature . It is observed experimentally that the product of this dimerisation is specifically the endo product 2.

To begin to understand why the endo isomer is preferred over the exo both forms were constructed in 3D and MM2 geometry minimization calculation performed on both. This resulted in a total energy for exo isomer (1) of 31.88 kcal mol^-1 and for the endo isomer (2) exo isomer of 34.00 kcal mol^-1. Thus the endo isomer is actually higher energy than the exo which would suggest a kinetic pathway (i.e a more stable transition state). A kinetic route is also suggested by the fact that the reaction gives one product exclusively rather than a mixture of both isomers which you would typical expect for thermodynamically controlled reactions. The Jmol models of both molecules can be displayed below.

Fig 2: Possible products of hydrogenation

The initial hydrogenation of dimer 2 could potentially occur at either alkene site, assuming simple addition of H₂ gas, to give either 3 or 4 product.(Note: This will depend on the exact mechanism of hydrogenation which may have a preference depending on the local sterics/structure surround each alkene, as well thermodynamic properties of the product.This may become important when extra functional groups are added to various positions around the rings.) MM2 calculations of 3 and 4 were run to give the total energies listed in Table 1. It can be seen from this calculation that isomer 4 is predicted to be the lowest in energy therefore addition of H₂ to the alkene in the bridged ring is preferred over the outer the alkene. The breakdown of energy components (shown in Table 1 below) which make up the total energy show how the difference in bond angles, lengths, torsion, intramolecular forces lead to a lower energy for isomer 4. In particular looking at the "Stretch" and "Bend" energies which are a guide of how much the bond lengths and angles deviate from their ideal system, it can be seen that they are both lower for Isomer 4 and so the system is less strained.Elevation of strain in the bridged system is likely to be the key component of the calculated stability of 4. In an unstrained molecule the bond of alkene to substituent bond is 120^o. For the two alkenes in 2, the bond angle of the alkene nearest the bridged system is 107.65^o (average of the two C=C-R bond angles because of the slight asymmetry of the system)and for the outer alkene 112.75^o (averaged again). Thus there is a much greater degree of strain on sp² carbons in bridged ring because they are furtherst away from the ideal 120^o. Under thermodynamic conditons product 4 would be favoured because of the release of this strain over the smaller strain at the outer ring alkene site.

Table 1: Components energies for isomers 3 and 4

Isomer 3		Isomer 4
Component	Energy (kcal mol-1)	Component	Energy (kcal mol-1)
Stretch	1.2850	Stretch	1.0972
Bend	19.8955	Bend	14.5063
Stretch-Bend	-0.8371	Stretch-Bend	-0.8371
Torsion	10.7893	Torsion	12.4976
Non-1,4 VDW	-1.2336	Non-1,4 VDW	-1.0512
1,4 VDW	5.6248	1,4 VDW	4.5127
Dipole/Dipole	0.1620	Dipole/Dipole	0.1407
Total energy	35.6860	Total energy	31.1539

Fig 3: Possible products of hydrogenation of tert-Butyl derivative of 2

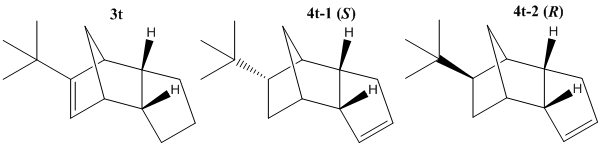
The calculation above suggests that elevating strain in the bridged system is likely to be the reason for selective hydrogenation of bridged ring alkene over the outer ring alkene. From a synthetic point of view it would be interesting to note what conditions lead to reversing the selectivity. To that end a tert-Butyl group was attached to one of the carbons on the bridged alkene. This choice was made because before hydrogenation the tert-Butyl group lies equatorial away from any steric clashes with the rest of the molecule, where as after hydrogenation (assuming it is still selective for this particular alkene) the tert-Butyl will be pointing up towards the bridgehead or down towards the other ring. If the latter two steric clashes lead to higher energy products than hydrogenating at the alternative alkene then it may be possible to induce selectivity for this alkene. Both MM2 and MMFF94 force fields were used to calculate relative energies of these isomers.

Table 2: Comparing total energies of hydrogenated t-Bu derivatives of 2

		Isomer 3t	Isomer 4t-1 (S)	Isomer 4t-2 (R)
MM2	Total Energy (kcal mol-1)	40.40	46.25	37.77
MMFF94	Total Energy (kcal mol-1)	62.66	76.74	64.27

Note: MM2 geometry optimisation was performed first before proceeding to calculate the MMFF94 minimisation.

The results show an interesting pattern. It is also important to note now the method/mechanism of addition of H₂ becomes important as different stereoisomers will be formed depending on which face of the alkene the H₂ is added. The results from the MM2 calculation would suggest that most stable product is 4t-2 where the tert-Butyl group is point upwards towards the bridge but the enatiomer, 4t-1 is actually higher in energy and also higher than hydrogenation at the other alkene, 3t. Thus according to this calculation the mechanism of _H2 addition is very important for controlling selectivity. However using the MMFF94 forcefield a different pattern is seen. It would seem to suggest, much more akin to the original hypothesis above, that 3t is most stable and that either enantiomer of 4t is higher in energy. This highlights the simplistic approach of these molecular mechanics forcefields which rely on differing sets of empirical parameters which can lead to different patterns observed between isomers. An approach which begins to calculate the electronic properties of these moleculars would lead to a more accurate representation of the system and hopefully a useful prediction of which isomer will be prefered in an actual synthetic reaction.

Nucleophilic addition to Pyridinium ring derivatives

Fig 4: Reaction 1 Nucleophilic addition of MeMgI to 5

Reaction 1

In this reaction a pyrdinium ring 5 attacked by the nucleophile 'Me^—' MeMgI, is thought to be highly stereoselective for product 6 with the absolute sterochemistry shown. This is suggested by a similar reaction carried out by A. G. Schultz et al. where 7 was reacted with MeMgBr.. They report a 19:1 selectivity for akylation at para position over the ortho and >99% stereoisomer selectivity. MMFF94 molecular calculation were carried out to try and determine why this reaction is selective for the stereo chemistry shown. In this example rather than looking at the absolute energy calculated specifically, the 3d geometry obtained around the reaction site will be examined for clues as to the reactions stereocontrol.

Fig 5: Screenshot of 3d Model of reactant 5

Fig 6: Screenshot of 3d Model of product 6

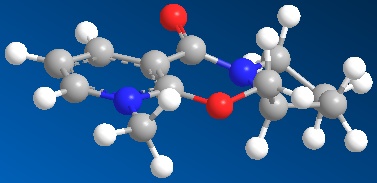
The lowest energy conformation found for the reactant 5 (using the MMFF94 minimisation) was reported to have a final energy of 57.48 kcal mol^-1. Working on the basis that this lowest energy conformation is the conformation the molecule is in as the MeMgI nucleophile approaches the geometry around the pyridinium ring, carbonyl of the lactam becomes very important (see Jmol). It can be seen that the pyridinium ring is effectively flat as you would expect for an aromatic system leading to no proference so far. When considering the carbonyl of the lactam (at the benzyl position) it is found to be point sligtly above the plane of the pyridinium ring(this description is based on orientating the molecule in the way shown in Fig 5). If in the transition state the Mg grignard species is co-ordinated to the carbonyl oxygen that would cause the Methyl to attack the ring at the para position from above the ring plane.

Fig 7: Reaction 2 Nucleophilic addition of PhNH₂ to 7

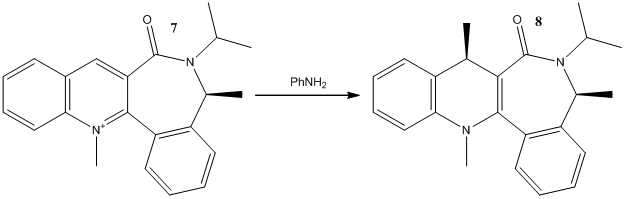
Reaction 2

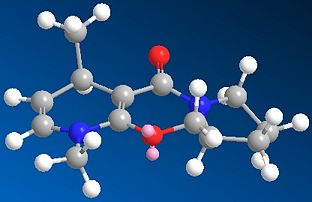
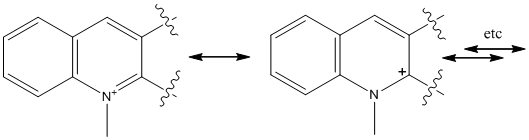
In similar reaction as 1, a quinolinium, 7, derivative reacts reversibly with primary and secondary amines to give stereoselective products used as chiral?amine transfer agents. Modelling of 7 produced some unusual results with the MMFF94 forcefield minimisation (similar results for MM2 but not shown here). The lowest energy conformation which could be found was 99.6592 kcal mol^-1. This seems unusually high and it can be seen that from image/Jmol in Fig 8 that the quinolinium N-Me is not planar as would be expected for an aromatic system. The calculation has opted to bend it upwards to avoid clash with nearby aryl ring and minimised to achieve the lowest energy conformation. This is a disregard for electronic properties of the aromatic ring which would confers electronic stability which may overcome the steric clash and lead to a planar structure in reality. There is suggestion amongst the academic staff the coding for "N+" has been changed in someway in the latest version of ChemBio 3D which allows the program to alter the planar geometry at this rather than defaulting to its approximation of an aromatic system. Whatever the case it could be argued that in reality ring may not be flat at all because of resonance stabilisation of the positive charge around the aromatic ring (fig 8). As the positive charge moves to the carbon on the right we are left with a tertiary amine species which are not flat and will try to adopt a trigonal pyramid structure as best it can because of the N lone pair repulsion. The new carbocation itself is effectively a benzyl cation which could be potentially stabilised by the outer aryl ring. These of course disrupt the aromaticity so is not that favourable but is likely to contribute in a small way to actual structure along with other resonance forms (the two shown being the ones presumed to be most dominant).

Fig 8: Screenshot of MMFF94 minimised geometry of 7

Fig 9: Resonance stabilisation

Because the geometry is key factor in predicting the specific reactivity of these compounds, a Semi-empiral Molecular orbital calculation (MOPAC, method=PM6) was performed to get a better approximation of the real geometry by including the electronic properties. This was to allow comparison of carbonyl geometry to the ring which is key to predicting the reaction stereoselectivity. The resulting structure (Fig 10) showed much less bending from planarity at the ⁺N-Me position which would now be more sympathetic to the aromatic nature of the quinolinium ring.

Fig 10: Screenshot of MOPAC(PM6) minimised geometry of 7

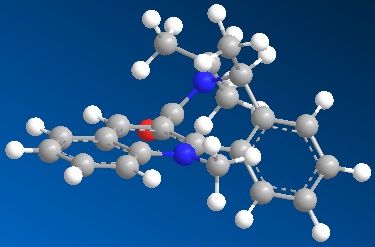
Unfortunately no X-ray crystal structure has been recorded for this molecule which can be found, but that would be the best way to determine the actual structure and ascertain how good a representation the various model geometries calculated actually are (true for all models generated in this report). It is also important to note, both for the structure and reactivity, the counterion is not shown which could have a large impact on both depending on how, how strongly and perhaps where it co-ordinates to the molecule. This is done to make the calculations easier as it becomes much more complicated when a component is not explicitly bound to a part of the molecule or is just loosely bound.

Returning to predicting the reactivity of 7, it can be seen from both Figs 8 and 10 that the Carbonyl is pointing down from the plane of the ring (quite dramitically so in MOPAC calculated geometry (fig 10)). Because this reaction is just simple nucleophilic attack it will preferentially attack the ring from above so as to avoid clashes of the Ph-N with the carbonyl. The MMFF94 optimised geometry (Total Energy: 38.88 kcal mol^-1)of the product is shown below in Fig 11.

(TALK more about what lit says)

Fig 11: Screenshot of MMFF94 minimised geometry of product 8

Reactivity of intermediates in the synthesis of Taxol

Fig 12: Isomerisation of 9 to 10

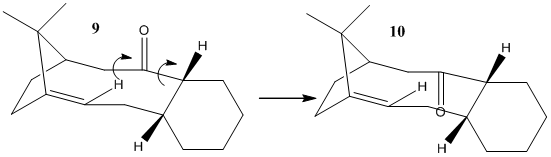
Taxol is important drug used in the treatment of ovarian cancers. During the synthesis of such a compound a key intermediate, 10 is synthesised in either that form or 9 but upon standing this mixture isomerises completely to 10. The relative energies calculated for these two isomers, using the MM2 forcefield, are: For 9 - 58.12 kcal mol^-1 and for 10 - 50.60 kcal mol^-1 (The same pattern is observed with the MMFF94 forcefield). The key difference is geometry of the carbonyl in each isomer, which on the face of it does not immediately suggest more stability in 10 over 9 as steric clash is minimal in both optimised isomers. When rotating these bonds which allow the carbonyl to point downwards other aspects of the ring structure must change and adopt a more favourable/stable geometry. The attached cyclohexane ring in 9 would appear to be a twist-boat structure which is higher in energy than the more boat like structure adopted in 10. However neither these approach the truely stable chair conformation of a cyclohexane ring. There is suggestion that this could occur by an retro-oxy-cope rearrangement into a norbane ring with attached cyclohexene and then back again into the more stable isomer. However refluxing toluene is needed to achieve this and the example they use has an OTBS group alpha on the cyclohexane ring opposite side to the carbonyl and alpha to fused ring position. Where as this particular molecule apparantly isomerisers on standing it seems unlikely and also it appears the carbonyl pointing down in the first place maybe key to this rearrangement occuring.

A final observation is that although this is claimed to be an intermediate in the synthesis of taxol, it lacks any functionality around the cyclohexane ring, yet the final product Taxol has two oxygen based functional groups and a further fused oxocyclobutane ring which would seem hard to introduce into an cyclicalkane. In a total synthesis reported by P. A. Wender et al. the functionalised cyclohexane ring is built onto the bridged cyclodecane ring where the carbonyl is protected and it is deprotected much later in the mechanism. There is so much other functionality that in the molecule at this point that it makes this model a to simplistic representation to understand whether the carbonyl is point upwards or downwards and which is the more favourable confirmation. Other total synthesis may exist but there is insufficient time to review them all.

Fig 13: Isomer 9

Fig 14: Isomer 10

Modelling using semi-empirical Molecular Orbital Theory

Up until this point, the calculations that have been carried out have largely focused on the mechanics of the systems, minimising the geometry to relative to a set of empirical parameters, largely trying to achieve the ideal bond angles and lengths set out in perfect sp3 and sp2 (and sp though not in this project) systems without breaking the molecule (the initial constraints). But that is only half the picture the electronic state of a molecule has great impact on reactivity, selectivity and even the geometry of a molecule (see discusion of aromatic systems above. This sections shows an example calculation which begins to aproximate the molecule orbitals

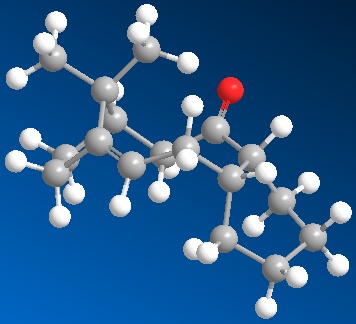
Regioselective addition of a dichlorocarbene

Fig 15: Dichlorocarbene addition to 12

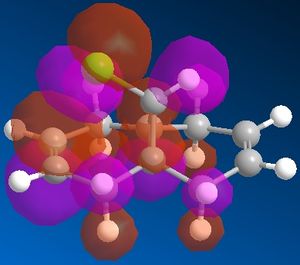
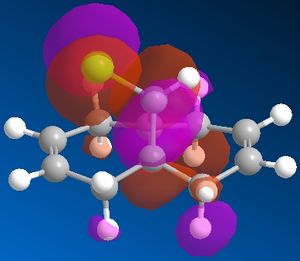
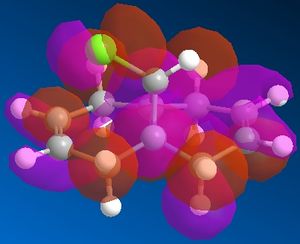
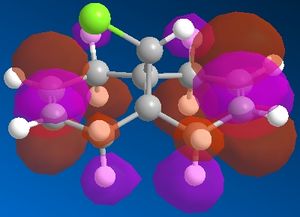
In this system we have a diene 12 which will react with electrophilic agents such as dichlorocarbene. An appreciation of the molecular orbitals would be needed to understand any particular selectivity electrophiles have for reacting with one alkene or the other because the molecule is almost completely symmetrical and the Cl is to far away to influence the reaction in any steric or geometry way (ignoring the possibility of any acceptionally bulky electrophile or chelation to Cl in the reaction mechanism). The Molecular orbitals calcualted usign MOPAC/PM6 are displayed below in Table 3 (LUMO-2 to HOMO+2):

Table 3: Molecular orbitals of 12

HOMO	HOMO-1	HOMO-2
LUMO	LUMO+1	LUMO+2

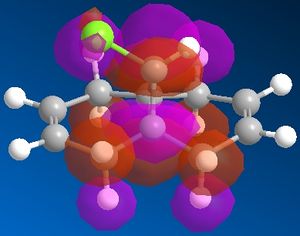It can be seen that the HOMO of the molecule that almost of all of the electron density in this orbital liesaround C-Cl bond and alkene on the same face as said bond. Thus most nucleophilic (or electron rich) alkene is this one and is where an electrophile would preferentially choose react. Though in the case of dichlorocarbene it is so highly reactive that this selectivity maybe reduced or not seen at all as it quite likely react with either alkene depending of geometry of attack. The HOMO-2 shows quite a lot of electron density around the other alkene and although lower in energy than the HOMO it may still be nucleophilic enough for the carbene to react with.

In order to investigate the effect of the Chlorine in the molecule of this nucleophilic double bond the vibrational spectra was calculated for this and dihydro derivate on side of the Cl bond. This was done using Gausian 09 program (with MM2 geometry minimisation in ChemBio 3D first) and the B3LYP/6-31G(d,p) method and basis set. The results were that C=C vibrations were 1737.05 cm^-1 opposite Cl-C(4.19 intensity), 1757.35 cm^-1 nearest C-Cl (3.93 intensity) for molecule 12 and for molecule 13 oppsite C-Cl, 1736.83 (3.2 intensity). Apart from a slight reduction in intensity there peak for this particular alkene shifts would seem to more or less the same. It is not clear what was meant to be obtained by this calculation? If we wished to know the effect of the C-Cl bond on the vibrational frequences of this alkene in this molecule would it not be better to replace the C-Cl bond with C-H (and/or C-Me, C-F, C-Br etc) and then compare??

Vibrational spectrum of 12 and 13 here

Structure based mini-project: Investigating regioisomers in an Intramolecular Schmidt Reaction

Fig 16: Intramolecular Schmidt Reaction in synthesis of a fused and bridged Lactam

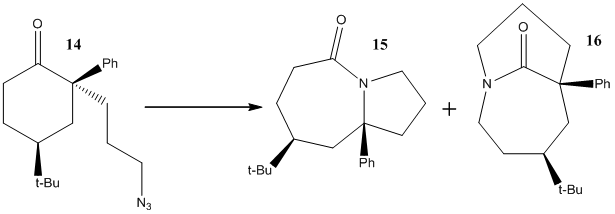
The Schmidt reaction was discovered in 1924 by Karl Schmidt when he reacted Benzophenone with hydrazoic acid (HN₃) to produced Benzanilide. The ability to insert Nitrogen between a carbonyl and carbon alpha to it has been exploited to produced lactams by tethering the azide to to the carbonyl then under acidic conditions the Schmidt reaction occurs with formation of a new amide bond which is a lactam. In example being studied the carbonyl is already attached to a ring and thus the reaction produces a bicylic system normally in the fused isomer but the authors of this paper were trying to find a way to encourage formation of the bridged isomer. (See Fig 16)

They found that by adding a π-sytem alpha to the carbonyl they could encourage the formation of the bridged system with MeAlCl₂ as the Lewis acid catalyst. The ratio products was 74:26 of products 16:15. This π-sytem alpha to the carbonylis thought to stabilise the N-N₂+ intermediate species in such a conformation that leads to bridged structure. The intermediate conformation which would lead to the other structure is not stabilised by this interaction as phenyl group is in pointing in the opposite direction. (See Scheme 7 in reference). The tert-Butyl group positioned axially opposite the carbonyl is also necessary according to the authors for the reaction to proceed with the desired selectivity.. A useful extension to this product would be to model these intermediates and compare relative energies however they are not simple species as they involve co-ordination of a lewis acid and non-specifically bound counterion.

The aim of my calculation was to check whether the NMR (¹³C) and IR assignments reported for the two isomers 15 and 16 were correct and also to see how well calculation of such properties compares with experiment. Below are the tables containing the calculated and reported NMR and IR data.

Table 5: NMR (¹³C)for Isomers 15 and 16 (literature and calculated)(ppm)

Isomer 15				Isomer 16
Atom No	Calculated	Literature	Difference	Atom No	Calculated	Literature	Difference
6-C	170.4*	172.4	-2.00	7-C	181.4*	184.4	-3.02
12-C	144.9	147.1	-2.16	12-C	145.3	147.6	-2.27
17-C	125.5	128.5	-3.04	20-C	125.0	128.5	-3.50
15-C	125.0	126.8	-1.81	17-C	123.8	126.2	-2.36
16-C	122.5			21-C	1123.5	126.1	-2.59
14-C	121.5	124.8	-3.25	18-C	123.4
18-C	120.0			19-C	121.9
2-C	67.6	68.6	-1.03	6-C	58.6	56.2	+2.40
5-C	49.7	47.5	+2.22	9-C	53.7	54.8	-1.14
3-C	49.0			2-C	49.7	50.2	-0.54
9-C	44.2	43	-1.23	5-C	48.9
10-C	39.3	41.4	-2.07	4-C	43.2	44.1	-0.85
7-C	37.3	39.3	-2.04	10-C	39.1	43.1	-3.97
13-C	34.4	33	+1.40	13-C	35.6	37.6	-1.14
19-C	29.9	32.6	-2.74	14-C	30.8	34.1	-3.33
21-C	28.8	27.1	+1.71	15-C	30.3
4-C	24.0	24.6	-0.63	3-C	27.84	28	-0.15
20-C	22.6			11-C	23.5	26.1	-2.58
8-C	21.9	19.7	+2.24	16-C	22.8	22.4	0.41

* These values have been corrected for systematic error sometimes found in carbonyl according to formula 0.96δ + 12.2 as suggested in script. The original values were 164.8 and 176.2 respectively

The first obvious difference in calculated NMR data and literature data is the gaps in the literature (19 compared with 15). The calculation has calculated the NMR as a snapshot in time but in reality the t-Butyl and Phenyl groups are free to rotate which average the chemical shifts of the carbons as they are never in one particular orientation with respect to the ring system (which is what the calculation assumes). It is therefore expected that t-Butyl methyl groups would be one sigal (3-1= loss of 2 signals) and phenyl carbon to average into 4 shifts (loosing the two signals for addition two carbons in the middle), explaining the loss of four signals 16. However in 15 there are 16 signals which might mean there is a barrier to rotation of one the groups and we start to see the appearance of individual signals.

The literature prediction of structure with NMR data would seem to correct according to this calculation as the as most chemical shifts are with +/-2ppm and the amide carbon peak has the corrected ordering predicted in the literature (lower shift for 15 when compared to 16).

The IR was calculated to compare with literature where they gave only peak. You would therefore assume that it is Amide stretch as this is most indicative signal in the IR for these compounds (the rest of the molecule is just made up akyl and aryl units).

Table 6: IR Data for Isomers 15 and 16 (literature and calculated) (cm^-1)

Molecule	Calculated	Scaled	Literature	Error (%) (Calc:Lit)
Isomer 15	1734	1667	1635	6.05
Isomer 16	1755	1687	1685	4.02

At initial glance the IR calculation would seem to be quite off but in terms of error they are within the 8-10% expected systematic error for these types of calculations. A scaling factor was sought to account for this systematic error and closest factor that could be found (in terms of the calculation method and type used, B3-LYP/6-31G(d)) was 0.9614. This and other such factors are calculated by comparing experimental and calculated IR data for many compounds. This does seem to bring the IR data closer to the literature reported values though it is still out for isomer 15. Given the good agreement in the NMR it is unlikely there is conformational difference giving rise to this error (especially as it quite a large difference for a typical amide). Importantly though the order IR peaks for the amide is the same way around as in the literature (i.e. the stretch is higher for Isomer 16 than 15).

The evidence presented him would seem to suggest that the authors of this reaction did indeed get the NMR assignment correct and that the calculations were successful at predicting real world properties to within a small margin.