Vincent Picton Transition States Wiki

Introduction

Minima in potential energy surfaces

In a potential energy surface (PES), a minimum is defined by a point where the first differential of the point is zero, and all second differentials are larger than zero (positive). This can only be represented in a system with up to 2 degrees of freedom, but in our calculations we have 3N-6 degrees of freedom, as there are 3N-6 normal modes for a molecule where N=number of atoms in molecule. In real terms a minima corresponds to a certain configuration of atom positions that leads to the overall structure having the lowest energy it can, this could either be within a range of possible similar configurations (local minimum) or of all possible configurations (global minimum). There may be several minima (local minima) on a surface, but only one global minimum, which is defined by the point with the lowest energy value (and will also of course obey the mentioned mathematical conditions). At a minimum all force constants are positive, and therefore all vibrations have positive frequency. One can tell if a minimum has been found by running a frequency calculation and making sure this is the case.

Nf710 (talk) 13:09, 16 January 2018 (UTC) How are the force constant and the vibrations related? Good understand of the PES in Guassian

Transition states in potential energy surfaces

On a PES a transition state corresponds to the maximum on the minimum energy pathway for a reaction. This can only be represented in up to 2 dimensions since energy occupies the third dimension. In the true PES of a molecule there are 3N-6 normal modes where N=number of atoms, and this means there are 3N-6 dimensions, but the method for finding the transition state still holds. The calculation involves finding the second derivative of energy (force constant) at each point where the first derivative of energy is zero. One of the points with a first derivative of zero will have a positive second derivative for every normal mode but one, which will be negative (ie this one mode has a negative force constant), and this point is the transition state. Running a frequency calculation will allow determination of whether a TS has been found, if the calculation is a success a single negative vibration frequency will be seen, corresponding to the single negative force constant produced by the second derivative of the only degree of freedom at an energy maximum.

Nf710 (talk) 13:11, 16 January 2018 (UTC) You can get all the force constants from the eigenvalues of the hessian matrix. (The matrix of second derivatives)

Basis sets

A basis set is a set of atomic basis functions which can be combined in various ways to respresent MOs in the LCAO used to solve the Hamiltonian. The requirement for a good basis set is it is able to represent the molecular orbitals accurately, and must not use so many functions to describe an orbital that the process becomes inefficient. Therefore the speed and accuracy of calculations in Gaussian is depend on a good basis set of atomic orbitals to represent the formed MOs. The basis set when combined in various ways allows the computer to shape MOs so one can see where electrons lie for an orbital. [1]

Nf710 (talk) 13:12, 16 January 2018 (UTC) Good basic understanding here. Some equations showing the maths of what they actually are would have been cool.

Gaussian Calculation methods

Only 2 levels of accuracy are employed in this project: the PM6 level calculation and the B3LYP level. For the vast majority of calculations the semi-empirical PM6 method is used, an inexpensive calculation which is based on the Hartree-Fock method but uses approximations and empirical data to vastly reduce processing power required to solve the Hamiltonian. For example semi-empirical calculations also often employ the zero differential overlap approximation, where 2 electron repulsion integrals are ignored to reduce processing time. The cost of this faster method is that results are not totally accurate, and can turn out to be totally wrong. [2] [3]

The second calculation employed is the higher level B3LYP which uses Density Functional Theory (DFT), a mechanical modelling method, to calculate all terms of the Hamiltonian except the exchange correlation term which is approximated; a portion of the exchange correlation term is found with the Hartree-Fock method and a portion from empirical data. [4] [5] This results in a more accurate calculation which requires a much longer time to compute.

Nf710 (talk) 13:14, 16 January 2018 (UTC) Nice. This is a good section you have clearly done further reading and gone beyond the script.

Methods used to find transition state

Three methods were employed in this piece of work in order to locate correct transition states from calculations. The first and simplest method involves simply drawing a guess transition structure by hand in Gaussview, and simply running a transition state calculation. This method requires explicit knowledge of the TS before beginning, or else no results of value can be obtained.

Method 2 involves making a guess of the TS structure, but before a TS calculation is done the bonds forming in the reaction are set to a specific value gained from empirical data. These lengths are then frozen, an optimization is run on the frozen structure, and only then is a TS calculation run. This is much more reliable than method 1 since we are giving Gaussian a much better guess structure than before.

Method 3 is near identical to method 2, except rather than guess a TS structure, an optimized product or reactant is the starting point. The bonds forming or breaking in the reaction are modified to empirical values, and again frozen for a second optimization. Finally a TS calculation is run. Method 3 is highly reliable, as we are determining a correct guess structure mathematically before attempting to find the actual transition state.

General notes

Throughout this report energy values will be quoted. Unless otherwise specified the units for these values is Hartrees.

The energy values used for the reaction energy barriers and reaction energies were calculated from appropriate frames in the IRC files, not from individually drawn out and optimized structures, this is so values are more comparable since they originate from the same PES.

Nf710 (talk) 13:14, 16 January 2018 (UTC) Overall really good section, some equations/pictures would have been nice to break up the text.

Exercise 1

(Fv611 (talk) Very well done throughout the whole exercise. Great job!)

Reaction scheme:

MO diagram and Jmols

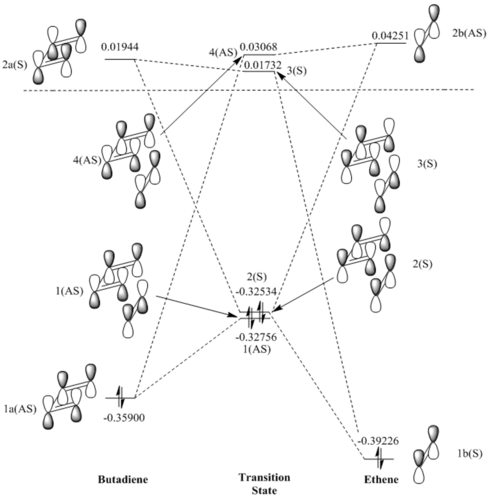
JMol files for TS and reactants in reaction between ethene and butadiene

Transition state orbitals

Butadiene orbitals

Ethene orbitals

2(S), E = -0.32534, HOMO

3(S), E = 0.01732, LUMO

2a(S), E = 0.01944, LUMO

1b(S), E = -0.39226, HOMO

1(AS), E = -0.32756, HOMO-1

4(AS), E = 0.03068, LUMO+1

1a(AS), E = -0.35900, HOMO

2b(AS), E = 0.04251, LUMO

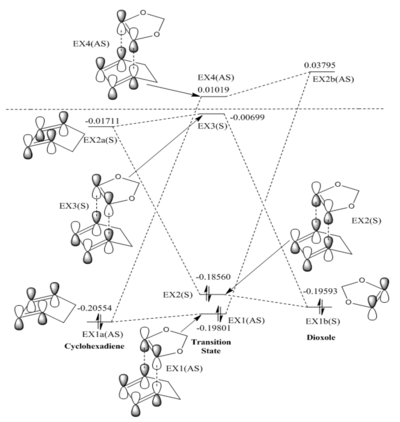
Analysis of MOs

From the calculations and visualizations of MOs available in figure.1, we can see that only two orbitals of the same symmetry can interact as this is the requirement for the overlap integral to be non-zero. This is exemplified by noting how within the MO diagram, orbitals 1b(s) and 2a(s) interact to give 2(s) and 3(s) in the transition state, while 1a(AS) and 2b(AS) interact to give 1(AS) and 4(AS). Orbitals of different symmetry have not interacted whatsoever, and only orbitals with like-symmetry have formed new MOs in the TS. One can further conclude from this that an a reaction will be "allowed" when the reactants have orbitals of like-symmetry that can interact to yield new MOs, and lower the energy of the system, one must also recall that only orbitals of close enough energy can interact to any significant extent, so the like-symmetry orbitals must also be of similar enough energy. A reaction will be "disallowed" if there are no orbitals of like-symmetry that can interact to lower the energy of the system.

Looking at the reactants in the MO diagram, the energetically closest orbitals of like-symmetry are the 1a(AS) and 2b(AS) (with 0.40151 hartrees difference vs the larger 0.41170 of the symmetric pair)), or in other words the HOMO of the diene and LUMO and the alkene. This is therefore the strongest interaction, and leads to the formation of 1(AS) and 4(AS) which of course have a larger splitting than the two symmetric TS MOs. This means that in relative terms, we have an electron poor dienophile and an electron rich diene (since the dienophile MOs are lowered in energy relative to the diene's), and so according to the definition the reaction is a normal electron demand Diels-Alder.

In the TS MO diagram, the electrons involved have visibly gained energy, and therefore the TS energy is as expected higher than the reactants alone. This nature of the TS creates the energy barrier that any reaction must overcome to proceed.

Two orbitals of opposite symmetry would have an overlap intergral of zero, and this can be intuitively seen by for example thinking about the interaction of 1b(S) and 1a(AS). In this example the left lobe of 1b(S) can interact with the left lobe of 4a(AS), but this constructive interference is cancelled out in equal proportion by the destructive interference interaction of the two right lobes, so overall we have zero overlap, and this will always be the case for two orbitals of opposite symmetry. This situation is highlighted below in Table.1

Table.1
Overlap integrals for symmetric (S)/antisymmetric (AS) interactions:
AS with AS:	Non-zero
S with S	Non-zero
AS with S	Zero

Analysis of bond lengths

Table.2: Carbon-carbon bond lengths from optimizations
C-C Bond length (Å)	Ethene	Butadiene	Transition State	Cyclohexene
C1-C2	-	1.33343	1.37972	1.50084
C2-C3	-	1.47078	1.41118	1.33696
C3-C4	-	1.33343	1.37965	1.50084
C4-C5	-	-	2.11548	1.53716
C5-C6	1.32749	-	1.38169	1.53461
C1-C6	-	-	2.11449	1.53715

Table.3: Typical C-C bond lengths: [6]
Bond	Length (Å)
Sp³-Sp³	1.54
Sp²-Sp²	1.34

Typical Carbon Van Der Waals radius = 170 pm = 1.7 Å [7]

Data collected from Gaussian on the C-C bond lengths of the TS is shown in table.2. C2-C3 in the TS is the forming C=C bond and is therefore shortening during the reaction, and between a C=C and C-C bond length, slightly closer to the C=C.

C4-C5 and C1-C6 in the TS are the forming sigma bonds, and are far longer than the typical C-C bond length. The distances between the Carbons are shortening during the reaction, the bonds are also far within 2x the Van Der Waals radius of carbon, showing their orbitals are interacting and in the process of bond formation.

C5-C6, C3-C4, and C1-C2 in the TS are all C=C bonds breaking to leave a sigma bond, therefore are lengthening during the reaction, and are above but very close to typical C=C length.

These observations all fit with theory, the TS is an intermediate between two molecules, and so the bonds forming/breaking in the reaction will be intermediate between the reactant and product bonds.

The breaking C=C bonds are all very close in length to a normal C=C bond, the forming C-C bonds are all much longer than a typical C-C bond, and the forming C=C bond is approximately in the middle of C-C and C=C.

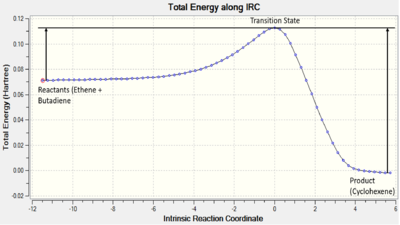
These observations, particularly of the breaking C=C bonds, suggest we are looking at an early stage transition state, where the TS bonds look very similar to the bonds in the reactants.

This fits with the IRC which shows a TS much closer in energy to reactants than products, illustrated in Figure.2, which is of course the definition of an early stage TS.

Also to note: during the reaction, Carbons 4, 5, 6, and 1 change from sp² to sp³ hybridisation, and carbons 2 and 3 remain sp² hybridised.

Below is a gif file of the IRC for this reaction.

Reaction path vibration

Below is the reaction path vibration in the TS, we see that in the vibration the forming C-C bonds appear to be the same length at all points, this is confirmed by the IRC where both bonds form in the same step. this means the bonds are formed synchronously. The vibration has a negative frequency due to it's negative force constant.

Figure.3: Negative frequency vibration in TS of reaction between ethene and butadiene

Log files

log file of IRC for exercise 1

log file of optimized cyclohexene for exercise 1, used in bond lengths

Exercise 2

Reaction Scheme:

MO Diagrams

(Fv611 (talk) As in the previous exercise, the MOs, MO diagrams and associated discussion are very good. Well done on mentioning the difference between exo and endo MO energies.)

Figure.4: Transition state MO diagram for the ENDO transition state of reaction between Dioxole and Cyclohexadiene	Figure.5: Transition state MO diagram for the EXO transition state of reaction between Dioxole and Cyclohexadiene

Thanks to our energy calculations we are able to determine this reaction is an inverse electron demand Diels-Alder, defined by the strongest frontier molecule orbital interaction being between the HOMO of the dienophile and the LUMO of the diene. This occurs when the dienophile orbitals are higher in energy than the diene orbitals, and could be caused by either electron donating groups on the dienophile raising their energy or electron withdrawing groups on the diene lowering theirs. In this case the two oxygens in the dioxole are raising the orbital energies because the lone pairs on the oxygens are donating to the alkene double bond, making it electron rich and raising the energy of the pi and pi* orbitals.

Nf710 (talk) 13:19, 16 January 2018 (UTC) If you are going to compare the energies quantitatively you should do an energy calculation for the last point on the IRC with both reactants on the same PES. if you do them on separate PESs they have different Hamiltonian potentials and the relative energies are different.

Table.4: JMol files for Endo and Exo transition state MOs

Endo and Exo transition state orbitals

2(S), E = -0.19502, endo HOMO

1(AS), E = -0.19648, endo HOMO-1

3(S), E = -0.00462, endo LUMO

4(AS), E = 0.01543, endo LUMO+1

EX1(AS), E = -0.19801, exo HOMO-1

EX2(S), E = -0.18560, exo HOMO

EX3(S), E = -0.00699, exo LUMO

EX4(AS), E = 0.01019, exo LUMO+1

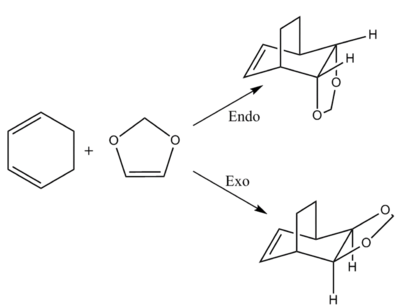
From viewing the above diagrams we can see that in the endo HOMO the oxygen lone pairs are able to interact with the cyclohexadiene pi system, unlike in the exo transition state. This will likely lower the HOMO energy and thus the overall transition state energy, and this is confirmed by the calculations, where this endo-only interaction seems to give rise to an approximately 0.005 Hartree stabilisation to the endo TS. In terms of steric differences between the two TSs there is seemingly very little to say. The only observation from the optimized models may be that the dioxole in the endo transition state has a slightly easier approach due to the flat sp2 hydrogens that the bulk of the dioxole molecule hangs over, vs the up-pointing sp3 hydrogens facing the dioxole in the exo TS. This difference is likely to be negligible for the overall TS energy in comparison to any orbital interactions that are playing a role.

Reaction barriers and energies

After running opt+freq calculations on the IRC frames (TS, reactants, product) at the B3LYP level, the following information was obtained.

Table.5: Energy data for reaction between 1,3-Dioxole and Cyclohexadiene
Product	Energy barrier (kJ/mol)	Reaction energy (kJ/mol)
Endo	159.81	-67.41
Exo	167.65	-63.81

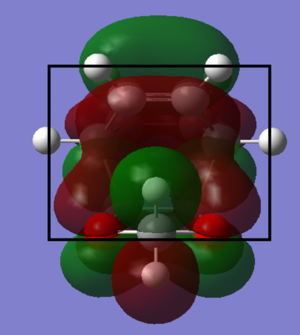
From these data it is clear that the endo is both the kinetic and thermodynamic product, defined by having the lower of the two energy barriers, and the larger energy release overall. The smaller energy barrier is as discussed earlier due to a favourable interaction between the oxygen lone pairs and the diene pi system, which stabilises the TS. While without data one may assume the exo product is thermodynamically more stable due to it's less sterically strained state, in reality the same stabilising interaction between oxygens and pi system as in the TS persists in the product, visualized in figure.6, lowering it's energy to below the exo product's. Due to these factors there would be little one could do to obtain a good yield of the exo product, as the endo will always dominate.

Nf710 (talk) 13:17, 16 January 2018 (UTC) There are is is steric clashing in the endo product which raised the energy.

Log files

log file of endo IRC for exercise 2

log file used to find thermochemistry of Dioxole (from IRC frame) for exercise 2

log file used to find thermochemistry of cyclobutadiene (from IRC frame) for exercise 2

log file used to find thermochemistry of endo transition state (from IRC frame) for exercise 2

log file used to find thermochemistry of endo product (from IRC frame) for exercise 2

log file of exo IRC for exercise 2

log file used to find thermochemistry of exo product (from IRC frame) for exercise 2

log file used to find thermochemistry of exo TS (from IRC frame) for exercise 2

Nf710 (talk) 13:20, 16 January 2018 (UTC) Well done you have come to the correct conclusion and your energies are correct. Good section.

Exercise 3

Reaction scheme:

IRC gifs

Cheletropic product formation	Endo product formation	Exo product formation

From these IRC calculations it is clear that the exo and endo pathways lead to asynchronous formation of the C-S and O-C bonds, but the cheletropic product forms both C-S bonds synchronously (both bonds form in the same frame). This could be attributed to the higher symmetry of the cheletropic transition state, and that both bonds forming are the same type (C-S rather than C-S and C-O), and so will be the same length in the products.

Thermochemistry data and reaction energy profile

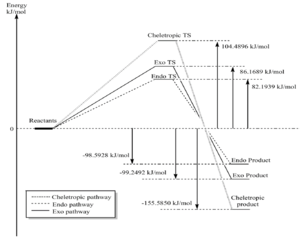
(You're quoting a very high level of precision Tam10 (talk) 14:43, 9 January 2018 (UTC))

Table.6: Thermochemistry data yielded from PM6 calculations on the endo, exo, and cheletropic pathways.
Pathway	Energy barrier (kJ/mol)	Reaction energy (kJ/mol)
Cheletropic	104.49	-155.59
Endo	82.19	-98.59
Exo	86.17	-99.25

As expected with Diels-Alder, the endo product is the kinetic product, but the cheletropic product is the thermodynamic product. This is more easily seen in the energy profile diagram shown in figure.7. As we move from reactants to a transition state, the lowest energy and therefore most accessible TS is that of the endo, while the product that results in the greatest energy release (and so is most stable) is the cheletropic. The reaction could be controlled with temperature, to obtain the cheletropic product the temperature would be raised as high as the conditions allowed to allow the system to equilibrate and therefore reach it's thermodynamic minimum. If the endo product was desired a very low temperature would be ideal, stopping this equilibration occurring.

(You probably wouldn't be able to get the endo product at all. There is a TS that links endo and exo that is lower than both barriers Tam10 (talk) 14:43, 9 January 2018 (UTC))

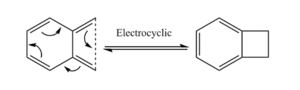
The Xylylene is highly unstable due to it's ability to undergo a unimolecular electrocyclic reaction to form an aromatic ring and a cyclobutane (shown in figure.8). In all three pathways we see this aromatisation occur, and this is in fact a main driving force for the reactions.

High energy alternate pathway

Upon viewing the Xylylene molecule, it is clear that there are two sites where a Diels-Alder reaction could take place, again with an endo and exo product to examine. The reason for the diene within the ring not reacting is revealed by further calculations using Gaussian.

Table.7: Thermochemistry data for alternative Diels-Alder pathway
Product	Energy Barrier (kJ/mol)	Reaction Energy (kJ/mol)
Exo	121.08	21.97
Endo	113.24	17.51

First from table.7, it is easy to spot that the energy barriers to both these pathways far exceeds even the cheletropic reaction seen earlier, this means that these reactions will occur with a much slower rate than the alternatives. Secondly these products have higher energy than the reactants, meaning these are endothermic reactions and are not thermodynamically favoured. This means these reactions simply will not occur, as they are vastly out-competed kinetically and thermodynamically by the alternative routes.

(Good Tam10 (talk) 14:43, 9 January 2018 (UTC))

Log files

Diels-Alder with normal diene outside ring

log file of cheletropic IRC for exercise 3

log file of cheletropic TS used for thermochemistry (from IRC frame) for exercise 3

log file of optimized cheletropic product used for thermochemistry (from IRC frame) for exercise 3

log file of optimized SO2 used for thermochemistry (from IRC frame) for exercise 3

log file of optimized o-Xylelene used for thermochemistry (from IRC frame) for exercise 3

log file of endo IRC for exercise 3

log file of optimized endo TS used for thermochemistry (from IRC frame) for exercise 3

log file of optimized endo product used for thermochemistry (from IRC frame) for exercise 3

log file of exo IRC for exercise 3

log file of optimized exo product used for thermochemistry (from IRC frame) for exercise 3

log file of optimized exo TS used for thermochemistry (from IRC frame) for exercise 3

High energy alternate pathway

log file of endo product IRC for extension to exercise 3

log file of optimized endo product used for thermochemistry (from IRC frame) for extension to exercise 3

log file of optimized endo TS used for thermochemistry (from IRC frame) for extension to exercise 3

log file of exo product IRC for extension to exercise 3

log file of optimized exo product used for thermochemistry (from IRC frame) for extension to exercise 3

log file of optimized exo TS used for thermochemistry (from IRC frame) for extension to exercise 3

log file of optimized SO2 used for thermochemistry (from IRC frame) for extension to exercise 3

log file of optimized o-Xylylene used for thermochemistry (from IRC frame) for extension to exercise 3

Extension

Reaction scheme:

MO analysis

The HOMO and LUMOs of the reactants, transition state, and products of the ring opening electrocyclic reaction of dimethyl meso-3-cyclobutene-1,2-dicarboxylate is shown below. This reaction proceeds via a conrotatory mechanism and the reaction is more accurately described as an equilibrium, further analysis will explain the conrotatory behaviour.

Table.8: HOMOs (top) and LUMOs (bottom) of the Reactant, TS and product of the butadiene ring closing reaction

Product (hexa-2,4-dienedioic

acid dimethyl ester)

Transition state

Reactant (dimethyl meso-3-

cyclobutene-1,2-dicarboxylate)

HOMO of Product

HOMO of TS

HOMO of reactant

LUMO of product

LUMO of TS

LUMO of reactant

Figure.9a: LCAO representation of ring opening conrotatary mechanism

(Wrong rotation to form the HOMO, but it's not really an issue Tam10 (talk) 14:56, 9 January 2018 (UTC))

Figure.9b: LCAO representation of ring closing conrotatary mechanism

Forwards, ring opening perspective

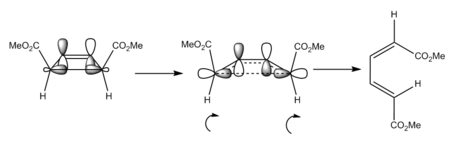
During the ring opening reaction, the sigma bond most easily visible in figure.10, but also in the TS HOMO JMol must break to form the pi system visible in the HOMO of the diene, the mechanism using the LCAO approach for which can be seen in figure.9b. In order to result in the correct phases in the antisymmetric HOMO of the diene, both carbons 1 and 4 of the opening butene ring must rotate in the same direction, therefore we have a conrotatory mechanism. This means the cis butene ring (both priority groups on the same of side of the ring) is mechanistically bound to produce the E,Z diene.

Backwards, ring closing perspective

Viewing the HOMO of the aliphatic alkene and transition state, the rotation that the molecule undergoes in ring closing is clear. To form the shown sigma orbital seen near-formed in the TS above and in the HOMO-3 product MO provided in figure.10, the two ends of the diene must both rotate in the same direction since the orbital is antisymmetric. This is more clearly illustrated in figure.9b, where the LCAO representation shows how the rotation must occur for the like-phases of the p orbitals to interact. Due to this specific rotatory requirement the reaction is stereospecific (it can only lead to one stereochemical outcome).

As expected from the forward reaction, in order to obtain the cis cyclobutene you must start with the E,Z diene. Z,Z is highly unstable due to steric clash between esters and so is unlikely to be a real molecule, but the more stable E,E diene would result in a different stereochemical outcome - the trans diene (one ester pointing up and the other down).

Woodward-Hoffman analysis

Figure.11: Antarafacial W-H analysis

Figure.12: Suprafacial W-H analysis

A Woodward-Hoffman analysis can also be done, and is more practical to be done on the backwards ring closing reaction: there are 4 pi electrons in the diene, we can either choose to interact the terminal orbitals in a suprafacial (figure.12) or antarafacial (figure.11) fashion.

According to the W-H formula (4q+2)_s + (4r)_a = result, if we choose the suprafacial path we get a total value of zero from the equation (π₄s ie 4 pi electrons is not in sequence 4q+2 = 2, 6, 10... so gives a value of zero, and we have no antarafacial component so this also has value zero), so therefore a suprafacial (and therefore disrotational) interaction is not thermally allowed (but would be photochemically allowed).

However if we choose the antarafacial (and therefore conrotatory) path we get a value of 1 out of the formula (since π₄a fits with sequence 4r = 4, 8, 12... giving a value of 1, and we have no suprafacial fragment so this has value zero), and so the reaction is thermally allowed via this pathway.

Note that for a reaction to thermally allowed the formula must give an odd value, the formula works by each term taking a value 1 if the number of pi electrons of the fragment fits it's sequence, and zero if not.

IRC gif

Below is an IRC calculation of the reaction, with this movie the conrotation is very clear, and we can see why the sterochemical result is as it is.

Log files

log file of IRC for extension

(Very good section. You have a clear understanding of the MO rationale of the WH rules. You can approximate the results of a photo- reaction by looking the LUMO, or even better by running these calculations on the excited state Tam10 (talk) 14:56, 9 January 2018 (UTC))

(+8%)

Conclusion

During this project PM6 and B3LYP calculations were successfully used to find transition state geometries of three Diels-Alder reactions and a further electrocyclic ring opening reaction. Using computational methods like these can allow us to work out data in a matter of minutes, that could otherwise take months or years to generate empirically. Due to the limitations of the computers available the majority of calculations were done at the less accurate PM6 level, given more resources it would be beneficial to obtain more accurate information using B3LYP 6-31Gd or even 6-31Gdp calculations, but nonetheless the PM6 level performed as it was designed, and provided reasonably accurate information at a very low cost. Comparisons with literature and theory, for example with bond lengths, support the reliability of these computational methods.

The calculations provided thermodynamic data, reaction pathways, minimum energy configurations, bond lengths, and activation barriers for the three Diels-Alder reactions. It also allowed the analysis of the high energy pathway of the o-Xylylene reacting with it's 6-membered ring: a pathway not possible to analyse by carrying out a real reaction. This, I believe, highlights a key strength of the software: any conceivable possibility can be analysed using the software, giving data, no matter how impossible in reality.

Thanks to this data it was determined that the endo product in exercise 2 was both the kinetic and thermodynamic product - a somewhat surprising result due to the steric strain of the endo product, and that the cheletropic product in exercise 3 was the thermodynamic product albeit with a much higher activation barrier, while the endo product was again the kinetic product.

Mathematically accurate MO diagrams were able to be produced for exercises 1 and 2, demonstrating the symmetry requirements for orbital interactions, and using bond lengths and IRC calculations it was possible to notice the early transition state in exercise 1, and the same analysis could have been applied to any of the reactions in this project, which is some possible future work that could be carried out.

In summary computational chemistry methods allow data to obtained from reactions that have never even been run or can never be run, as well as well-known reactions. At minimum the calculations provide data that would take far more effort to obtain empirically. For this reason the use of computers in chemistry have pushed our knowledge of science further than ever possible before.

References

1. Joseph J W McDouall, 2013, " Computational Quantum Chemistry: Molecular Structure and Properties in Silico", RSC publishing

2. Jensen, Frank (1999). "Introduction to Computational Chemistry". Chichester: John Wiley and Sons. pp. 81–82

3. R. Hoffmann, 1963, J, Chem. Phys., 39, 1397

4. A. D. Becke (1988). "Density-functional exchange-energy approximation with correct asymptotic behavior". Phys. Rev. A. 38 (6): 3098–3100

5. S. H. Vosko; L. Wilk; M. Nusair, 1980, Can. J. Phys. 58, (8), 1200–1211

6. "https://ocw.mit.edu/courses/chemistry/5-12-organic-chemistry-i-spring-2003/lecture-handouts/04.pdf", 15/12/17

7. A.Bondi, J.Phys.Chem, 1964, 68 (3), 441-451