Rep:Mod:vh42bh43
Michael Hurhangee - Computational Module 3
The Cope Rearrangement
The aim of this computational experiment is to investigate the [3,3]-sigmatropic shift of 1,5-hexadiene, also known as a Cope Rearrangement.
Scientific consensus is that the rearrangement occurs in a concerted pericyclic manner through either a chair or boat transitions state.
To fulfil the aims of the experiment the low-energy minima (conformers) and the pericyclic transition structures, chair and boat, for the Cope rearrangement need to be determined on C6H10 energy surface.
Optimising the Reactants and Products
The first step is this computational experiment is to find the optimised structures for the reactants and products. For the Cope Rearrangement of 1,5-hexadiene, the reactant and product are both 1,5-hexadiene. However, the position of two π bonds and one σ bond have changed, which is important for substituted 1,5-hexadiene derivatives.
1,5-hexadiene has 3 C-C's in the middle it's chain. There is free rotation about σ-bonds and therefore 1,5-hexadiene has the ability to adopt many different conformers (local low-energy minima). The task is therefore to find the lowest energy conformer, which is the conformer which will be most populated.
Finding Conformers of 1,5-Hexadiene
To start the investigation with the lowest energy conformers of 1,5-hexadiene some simple conformational analysis can be applied. It is well known that butane has two thermally accessible conformers gauche and anti-peri-planar (a.p.p.). Therefore, the four central carbon atoms of 1,5-hexadiene can have their dihedral angles manipulated to app & gauche conformations, then their conformations can be optimised and the energies compared, see below for results.
The computational level of theory used to optimise the structures is Hartree-Fock with the basis set 3-21G (HF/3-21G). This is a relatively low end method for calculations and is used to gain a quick and cheap results.
It can be seen by comparing the relative energies for both conformers that the a.p.p. conformer is lower in energy. This is perhaps the expected result as the two most sterically demanding groups are as far apart as possible.
Finding lowest energy conformer of 1,5-hexadiene
In the above a.p.p. conformer the -CH=CH2 groups are still both on the same side of molecule, with respect to the plane of the C-C-C-C bond, therefore perhaps the energy could be lowered by positioning the alkene groups on opposite sides. The results for which are shown below.
It can be seen that this adjustment to the relative positioning of the alkene groups lead to a slight increase in the conformers energy. One could therefore assert with reasonable confidence that A.p.p. C=C same side (A.p.p. C2) is the lowest energy conformer for 1,5-hexadiene.
Comparison of calculated conformers to Appendix 1
Provided in the instructions is Appendix 1 which shows the energy and conformers for 1,5-hexadiene, the results from above can be then compared to those from Appendix 1.
| Calculated label and point group |
Calculated energy | Appendix 1 label and point group |
Appendix 1 energy |
|---|---|---|---|
| A.p.p. C2 | -231.69260 | anti1 | -231.69260 |
| A.p.p. Ci | -231.69254 | anti2 | -231.69254 |
The Gauche conformation included in tables previously is not included in Appendix 1, because it's energy is too high to make it into the 10 lowest energy conformers. In constrast, both the a.p.p C2 and Ci, were in the lowest 10, and shall be referred to as anti1 and anti2 respectively from now on. The energies of anti1 and anti2 match well between the calculations and the appendix. Showing that the calculations above have been performed correctly and that the HF/3-21G method can return consistent and repeatable results and therefore is likely to be adequate for this investigation. The most interesting observation from the Appendix 1 is that a gauche conformer has the lowest energy! This at first appears to be counter-intuitive as one would expect a a.p.p. conformer to be lowest energy due to steric reasons discussed previously. Therefore it is likely that the low energy gauche conformer favourable electronics interactions are also involved.
Comparison of computational methods in optimising anti2 conformer
The anti2 conformer (a.p.p. Ci) shall now be optimised by a more computationally demanding method DFT-B3LYP with basis set 6-31G*. The geometries of the anti2 conformers shall then be compared.
| Geometry parameters | HF/3-21G | B3LYP/6-21G* | ||||
|---|---|---|---|---|---|---|
| Structure | ||||||
| C9-C1-C4-C7 dihedral |
180.0o | 180o | ||||
| C11-C9-C1 dihedral |
124.8o | 125.3o | ||||
| C11-C9 bond length |
1.316Å | 1.333Å | ||||
| C9-C1 bond length |
1.508Å | 1.504Å | ||||
| C1-C4 bond length |
1.553Å | 1.548Å |
From initial inspection of the Jmol file it can be seen that both methods return geometries which are very similar. Upon comparing the bond angles and lengths is becomes clear that the structures are about 99% identical with only small deviations. Therefore, it can be concluded the HF/3-21G method is sufficient for the comparisons of geometries for the 1,5-hexadiene.
Frequency analysis of anti2 conformer
Finally, to check that that the anti2 conformer is in fact a conformer (low-energy minima) one must perform a frequency analysis to check that all the vibrations are real (positive). This was perform on anti2 conformer using B3LYP/6-21G*.
The low frequencies from the calculation were -
Low frequencies --- -18.6342 -11.7125 -0.0009 -0.0006 0.0003 1.8424 Low frequencies --- 72.7326 80.1452 120.0243
Since in the second row there are no negatives frequencies the anti2 conformer is a minima. The simulated spectra and the vibrations that appear in the spectra are shown below.

This simulated spectra can then be compared to a literature spectra[1]. Below is a table comparing calculated shifts to the literature ones.
| Calculated peak (cm-1) |
3234 | 3155 | 3137 | 3031 | 1734 | 1523 | 1289 | 1036 | 940 | 938 | 669 |
| Literature peak (cm-1) |
3079 | 2983 | 2925 | 2848 | 1646 | 1441 | 1214 | 998 | 914 | 914 | 652 |
From the above tabulated data it appears that all the IT active vibrations in the calculated model have corresponding peaks in literature IR spectra. The spectra of comparison look similar and have similar patterns such as the unusual peak at ~1700cm-1 and 4 distinct C-H peaks (~3000cm-1). However, all the calculated peaks are significantly larger than the literature values. With the greatest values having the largest difference of ~7.5% and the smallest values being 2.5% larger. This is a systematic error in the calculation that comes from the method treated the vibrations as harmonic oscillators. To calculate a more accurate spectra a anharmonic model must be used.
From the calculation it is also possible to find information about the energy of the conformer. The most important thermochemical information is included below.
Sum of electronic and zero-point Energies= -234.469212 Sum of electronic and thermal Energies= -234.461856 Sum of electronic and thermal Enthalpies= -234.460912 Sum of electronic and thermal Free Energies= -234.500821
Optimising the "chair" and "boat" transition structures
In this part of the experiment the transition structure will be investigated using a number of techniques, the reaction coordinate visualised and the activation energy calculated for both the "chair and "boat" transition structures.
Optimisation of transition state fragment
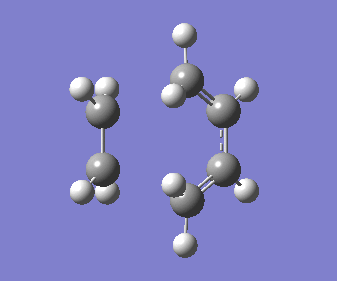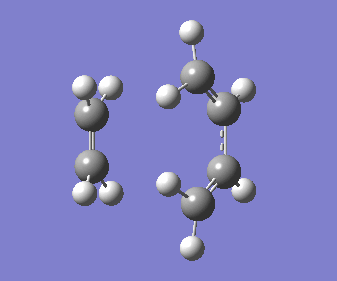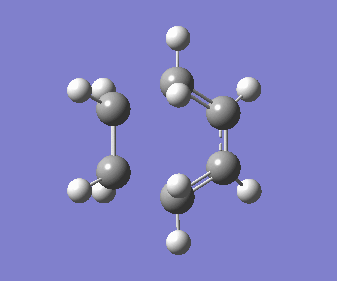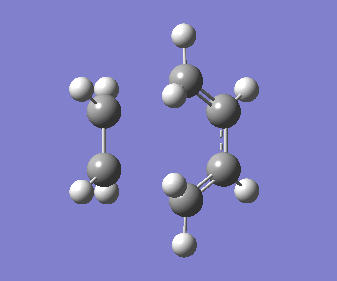
The transition states of the Cope rearrangement for 1,5-hexadiene are thought to be aromatic and progress as indicated by the image[2].

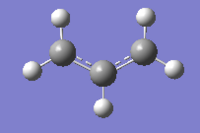
In the diagram above it can be seen that both transition structures progress with bond breaking/forming occurring inbetween two allyl fragments (CH2CHCH2). To model the transition structures this fragment must first be optimised. The fragment was optimised using HF/3-21G level of theory (which shall be applied throughout the transition state optimisations), which yielded the following structure.
Manual optimisation of "chair" transition state using TS(Berny)
The "chair" transition state can be found manually by using optimisation to a maximum. This is done by the calculation of the force constant matrix (the Hessian). At the maximum stationary point negative imaginary frequencies appear, this frequency should correspond to the Cope rearrangement.
To perform the manual "chair" transition state optimisation the allyl fragment was put into the Gaussview window twice. The fragments were then orientated so that they looked similar to the "chair" transition state. Using HF/3-21G level of theory they were Optimised to a TS (Berny).
It is vital to the this method of finding transition states that the fragments are orientated in a good guess transition structure. Otherwise,the method will not be able to find the correct TS due to farthe curvature of the potential energy surface being different at points far away from the maxima. In this case the terminal allyl carbon were placed ~2.2Å from the other terminal carbon.
The method provided the result with the following transition structure and imaginary frequency.
"Chair" transition structure (HF/3-21G - TS Berny)
|
"Chair" Cope rearrangement |
Manual optimisation of "chair" transition state using frozen coordinate method
In this method of manual TS optimisation the reaction coordinate is frozen and the rest of the molecule fully relaxed. Then the reaction coordinate is unfrozen and the transition state found. An advantage of this method is that it can avoid calculation of entire force constant matrix and instead differentiating along the reaction coordinate, resulting in a cheaper alternative to force constant matrix when it is expensive to compute.
To apply this method the terminal allyl carbons were set as a bond of fixed distance 2.2Å with frozen coordinates. The structure was then optimised giving a pseudo transition structure, i.e. it was like the TS except the bond breaking/forming distance had been frozen to 2.2Å. Next this constraint was removed and the optimisation set to run TS (Berny) as before but the Hessian was not calculated. The result of the calculation can be seen below.
"Chair" transition structure (HF/3-21G - Frozen coordinate method -TS Berny)
|
"Chair" Cope rearrangement |
Comparison of the two manual transition structure optimisation methods
The two methods provide identical results, to the degree of accuracy of such calculations. All terminal carbon inter-fragment distances, bond breaking/forming, distances are 2.02Å. Also, the central carbon inter-fragment distance at 2.88Å and the fragment bond angle is 120.5o .The results are identical, showing that the two methods found the same maxima on the potential energy surface. This result is expected as the same level of theory and method were used to find the TS, the only real difference in the method was how the fragment were initially orientated to one another.
Optimisation of "Boat" transition structure using QST2 method
A fully automated method of findiug transition structures is the QST2 method. This method shall be applied to the 1,5-hexadiene, the calculation works by taking both the products and reactants of a reaction and interpolating between the structures in an attempt to find a transition structure.

To apply this method both product and reactant structures are drawn into one Gaussview MolGroup. From this window the atoms are numbered so that the numbering shows the Cope rearrangement occurs. The QST2 method was then applied. This method failed to find the correct "boat" transition state. To help the QST2 find the TS, the structure of the reactant and product can be changed as to match better match the "boat" conformer (and TS sown in image previously). By improving the initial guess it increases the chances of the chance of the automated method of finding the TS. The reactant, transition structure are provided below.
| Reactant | "Boat" TS | Product | ||
|---|---|---|---|---|
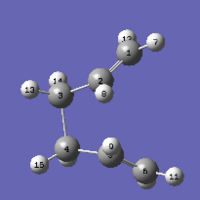 |
 |
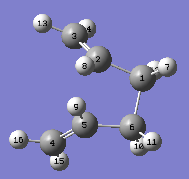 |
Following potential energy surface (PES) from transition structures to local minima
Following PES by inspection
The next step in understanding the Cope rearrangement is to know which conformers have access to the transition states.
On inspection it is hard to tell which conformers lead to the transition structure. Or in terms of the PES, which low energy minima and maxima are thermally accessible to one another. For the "chair" transition state, it is possible to imagine the transformation from conformer to transition state. When looking down the plane of the two chains, imagine pulling apart the bottom set of terminal carbons whilst pushing the top pair closer to give a structure similar to that of similar to that of gauche2 (if we ignore the double bond.For the "boat" transition state if you imagine looking down one of the bonding breaking/forming interactions and then rotating about the interaction, until you two fragments are a.p.p. to one another you get the anti2 structure.
| Transition state | Conformer | |||
|---|---|---|---|---|
Chair transition state
|
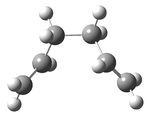 | |||
|
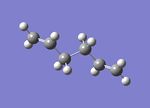 |
The above thought experiments show that it is possible to finding routes between conformers and transition states by looking. However, it is very hard to accurately estimate the energy barrier of such thought transformations. Therefore to get an accurate picture of which and how conformers transform into transition states a computational approach must be taken.
Following PES using Intrinsic Reaction Coordinate
This method automatically alters the geometry of the transition structure so as to follow the PES along where the gradient the steepest. The level of therory used for this entire IRC investigation was HF/3-21G.
In the current investigate the calculation is set up to follow the both the "chair" and "boat" transition state's symmetrical reaction coordinate (product & reactant are the same) in only one direction, calculate the force constant once and perform 50 points along the IRC to find the minima.
Using IRC to find minima of "chair" transition state
The IRC method was applied to the "chair" transition state as to find the conformer most closely related to it. The result from the IRC method with 50 points and calculate the force constants once is shown below.

It is clear from the above graph that the TRC method does not find a conformer, as the total energy does not reach a minima and the RMS gradient Norm is not very close to 0. To find the conformer most closely related to the transition state 3 options were available, perform an optimisation of the final IRC structure (method 1), restart IRC calculation specifying more points along the IRC so that a minima is found (method 2) and finally instead of calculating the force constant matrix only once we can make it calculate it at every step along the IRC (method 3). All these methods come this pluses and minuses, mainly cost and accuracy. Each of the three method shall now be applied to the "chair" transition state in an attempt to find the minima.
Method 1 gave the gauche2 with the correct energy straight away and was the quickest calculation. Demonstrating it's benfits as a method to assist IRC, however one should be aware that if the IRC is still far away from the minima the method can fail. Method 2 got the structure of gauche2 very well including the point group, but it's energy was just a slightly too high. Increasing the number of steps would remedy the problem or alternatively an optimisation would get the correct energy. The calculation was relatively quickly and got very close to the correct result however choosing the number of steps along the IRC is not the easiest thing to do. Finally, Method 3 didn't appear to get much further than the very first attempt we had, even though it was very computationally intensive compared to the other methods. It needed more steps to get a close energy, structure and point group. However, a quick optimisation from the structure it gave did lead to the conformer gauche2*.
To conclude the "chair" transition state is most closely related to the conformer gauche2.
Now the same IRC method will be applied to the "boat" transition state to find the conformer most closely related to the "boat" transition state. The IRC was applied to the boat using 150 steps and calculating the force constant only once.
After these steps the structure had not yet minimized and had the following structure
| Jmol of structure after 150 steps | IRC graphs | |||
|---|---|---|---|---|
|
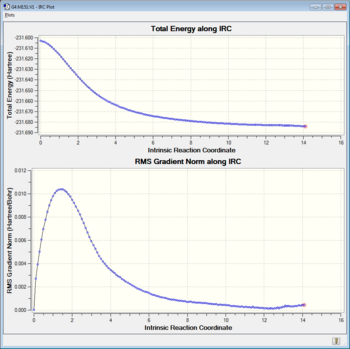 |
The Jmol structure above does not correspond to any of the conformers present in the Appendix 1, even thought the energy appears to be minimized. The structure had an energy of -231.68402 Hartree and a point group of C1
To check that this was in fact a minimum (and therefore conformer) a optimisation to a minimum was performed on the structure above. This resulted in the rather surprising (to myself at least) result that gauche3 (lowest energy conformer) was related to the "boat" transition state. The energy and point group matched the assignment of gauche3 perfectly.
Conclusion about finding conformers from transition states
From the thought manipulations above it was possible to guess which conformers were related to the transition states. It was later shown that one of the thought experiments did in fact predict the correct conformer "chair" transition to gauche2. However, the other prediction was absolutely wrong when compared to computational results. This shows that it may be possible to imagine the manipulation but it might not be the right one and there may be many other feasible manipulations that could occur.
The IRC found conformers which were related to the transition states. Th method was shown to have positives and negatives, such as somtimes falling short and requiring further work and in the case of the "boat" transition structure, giving a minima where perhaps no conformer existed. These problems can however be overcome with careful IRC management, as always in computational chemistry you must balance cost and accuracy, trying to achieve accurate results by doing quick as possible calculations.
Finding the activation energies for "chair" and "boat" transition state from the anti2 conformer
It is possible to compare the thermal chemistry data from the anti2 conformer and the transition states as to gain an understanding of the energy difference between the two states. This energy difference corresponds to the activation energy (energy to excite normal state to transition state). This can be done for the two different levels of theory, HF/3-21G and B3LYP/6-21G*, a lower and higher level respectively.
The energies calculated matched extremely well with those provided in Results Table[6].
The results shows that the low level method HF/3-21G does not provide results that can be compared to experimental values in general. The basis set as method are too simple. However, the energies it does produce are correct relative to other energies calculated in the same method, so this low level method is good to traverse the potential energy surface first and gain a relatively cheap and quick understanding of the surface. However, when one requires a in depth analysis with is comparable to experimental data, which is the goal of all computational chemistry really, then one must use a higher level of theory. This higher level of theory can be seen to correspond well to experimental data therefore justifying the results of the computational experiment as valid.
Diels-Alder Cycloaddition
Diels-Alder (DA) is a subclass of cycloadditions, which themselves are a type of pericyclic reaction. Specifically DA reactions are π4 + π2 cycloadditions. An example of which is the reaction of cis-butadiene and ethylene. DA reactions occur due to the favourable interaction between the HOMO-LUMO of the two reactants.

Cycloaddition of cis-butadiene and ethylene
In this part of experiment the cycloaddition of cis-butadiene and ethylene will be investigated.
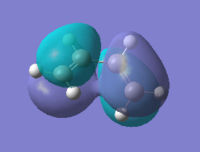
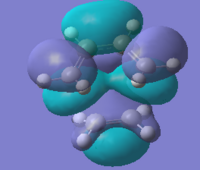
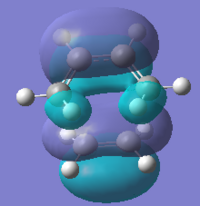
Frontier orbitals of butadiene and ethylene
The interactions of the cis-butadiene's HOMO and ethylene's LUMO and cis-butadiene's LUMO and ethylene's HOMO are vital to the sucess of the DA reaction. These MO's can be computed for both reactants.

Initially the semi-empirical AM1 method was used to optimise the structure of cis-butadiene. At first the structure of cis-butadiene was drawn planar with the dihedral angle C1-C4 = 0o. The structure was optimised and this gave the negative frequency. The imaginary frequency shows the molecule twisting as to lose it planar structure. The molecule was then re-optimised with the C1-C4 dihedral angle set to ~20o. At this point the method was switched from the AM1 method to B3LYP/6-31G* level of theory to get a more accurate result for the optimisation and molecular orbitals. The same process was then repeated for the ethylene molecule.
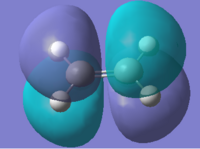
From the above symmetry assignment it can be seen that the HOMO and LUMO from each reactant have the same symmetry (anti- or symmetrical) they therefore interact and a cycloaddition could occur.
Transition structure of the Diels-Alder reaction between cis-butadiene and ethylene
The transition structure for the Diels-Alder reaction was found using the freeze coordinate method and placing the terminal carbons 2.1Å apart and then using the method as detailed previously. This lead to the transition state below with a imaginary frequency of (-)525cm-1.
The symmetry of both the HOMO & LUMO of the transition state are both symmetric. This result is expected from the HOMO and LUMO of the reactants. Two symmetric wavefunctions mixed result in a symmetric wavefunction; and two anti-symmetric mixed result in a symmetric wavefunction. The HOMO and LUMo can therefore be formed from either of the MO pairs described above. The HOMO of the transition state is made from the combination of the HOMO and cis-butadiene and the LUMO of ethylene and therefore the LUMO of the TS is made from the LUMO of cis-butadiene and HOMO of ethylene. The easiest way to see this assignment is to look at the nodal pattern in the LUMO of cis-butadiene and see how it matches near perfectly with the LUMO of the TS.
The bond lengths in the transition state shed a certain amount of light on what is going on in the reaction. For example the two pairs of terminal carbons are at 2.27Å apart, which is considerably less than twice the VdW radii of carbon, which is 1.72Å[7]. This implies that there is a positive bonding interaction between the terminal carbons.
Furthermore, for all the carbons in cis-butadiene and ethylene have bond distances which are considerably less than the normal sp3 C-C bond length of 1.54Å but larger than the normal sp2. Implying that there is some double bond characteristics for all the "old" carbon-carbon bonds including C4-C6 which is formally a single bond in the reactants. This information implies a delocalisation of the pi electron in the transition state, through both molecules. Giving the pericyclic reaction its characteristic aromatic transition state.
The imaginary frequency shows that the bond forming in the transition state is synchronous, i.e. both bonds form at the same time. This supports the view described above about the delocalisation of pi electrons and a aromatic transition state, as in the aromatic transition state the bonds would be formed equally at both ends and this would result in a synchronous formation. Therefore the imaginary frequency supports the pericyclic mechanism.
Activation energy for the cycloaddition of cis-butadiene and ethylene
During the course of the investigation the reactants and transition states were optimised to the B3LYP/6-31G* level of theory, this allows the activation energies of reaction to be investigated. The energy for cis-butadiene and ethylene are -155.99648 and -78.52746 Hartree respectively. The sum of reactants energy is -234.52394 Hartree. The transition state has can energy of -234.48282. Therefore, giving the activation energy to be 0.04112 Hartree which is ~108kJ mol-1 which is in good accordance with the literature 115 ± 8 kJ mol-1[8]. This once again shows that high end computational models can bring accurate results.
Diels Alder Cycloaddition of Maleic Anhydride and Cyclohexa-1,3-diene
The next cycloaddition to be investigated is the Diels-Alder cycloaddition of maleic anhydride and cyclohexa01,3-diene. Unlike the previous example this reaction can produce regioisomers as products, i.e. either endo- or exo- product. The below reaction progresses as to produce mainly endo product
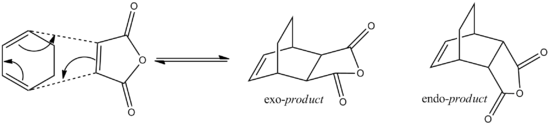
Optimisation of exo and endo transition states
Since the endo product is the least thermodynamically favoured product is formation implies that teh reaction is kinetically controlled. Therefore, to investigate the reaction a the transition structure of both the endo and exo production formation shall be computed allowing a quantitative comparison between the two.
| Properties | Endo TS | Exo TS | ||||||
|---|---|---|---|---|---|---|---|---|
| Energy | -0.05477 | -0.05050 | ||||||
| Imaginary frequency | 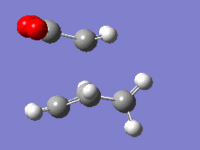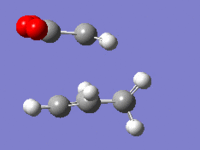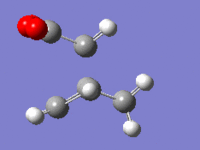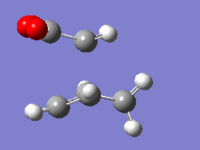 |
 | ||||||
| Bonding forming interactions |
2.10Å | 2.17Å | ||||||
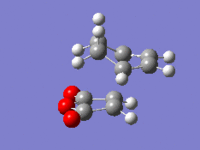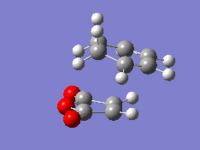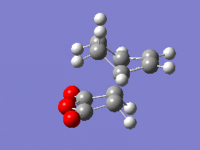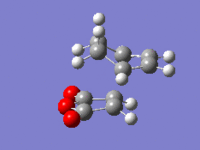
| Structure |
|
|
For both of transition structure there is only one imaginary frequency which corresponds to the formation of the endo and exo products respectively. Both the bond formations are synchronous indicating that the reactions are concerted pericyclic reactions, as expected, with the bonds showing similar properties and lengths to those described previously. This shows that the transition states have been located and that the correct reaction is occurring.
The transition state of endo is more stable by 0.00427 Hartree (11.2 kJ/mol). This is quite a difference in energy between the transition states, this difference is why the endo product is observed from the reaction however it does not say why there is a such a difference in energy.
Firstly from looking at the structures above the exo product appears to have an increased steric clash in the TS. The increased strain is from the -(C=O)-O-(C=O)- fragment being placed almost directly above the -CH2-CH2- fragment. The hydrogens of the later fragment are facing toward at the former, H's are 2.76Å from central oxgen, and this causes quite a large steric clash compared the endo TS. In the endo TS the fragment below -(C=O)-O-(C=O)-, is -CH-CH- the hydrogens of this fragment are point away from the oxygens, H's 3.63Å from central oxygen, and this therefore reduces steric clash resulting in a lower energy. However, from chemical intuition it is unlikely that this steric clash would lead to such a large energy gap an indicated above.
The strain of forming the bonds also may affect the energy of the TSs. For example the bond that is being made is going to be a single bond between the sp3 carbons and therefore ideally the bond angle should be ~109o. However, the angle between the CCC angle between the cyclohexadiene's double bond and the maleic anhydride's bonding forming is 99.4o and exo's is 92.7o. The endo's new bond angle is closer to ideal and would result in less strain in the transition state,
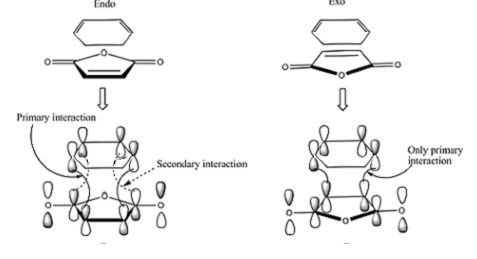
Another reason for the energy difference could be favourable secondary orbital interactions occuring in the endo TS, which will be discItalic textussed in detail below.
| Properties | Endo TS | Exo TS |
|---|---|---|
| Energy | 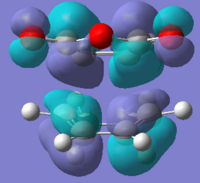 |
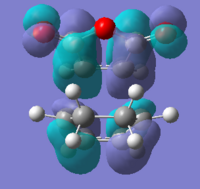 |
| Imaginary frequency | 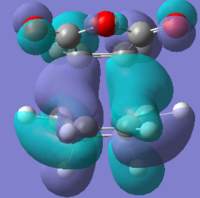 |
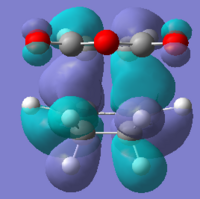 |
The HOMO and LUMO for both TS are all antisymmetric. The HOMO in both cases describes the newly formed sigma-bonding interactions between the terminal carbons of the reactants. With shared electron density between the two reactants being the driving force for the reaction to occur. The TS HOMO is made from the interaction of the HOMO and cyclohexadiene and the LUMO and maleic anhydride. The LUMO of maleic anhydride orbital is the π* antibonding orbital for C=C interaction. Therefore when it mixs with the homo of cyclohexadiene it causes the single bond to bond a double. The LUMO of both TSs has a nodal plane between the two reactants meaning that it is antibonding with respect to the new fragements.
As mentioned previously the secondary orbital interactions (SOI)[9] act to stabilise the endo and not the exo transition structures. In the endo transition structure the the inner carbons of the π-bonding system on cyclohexadiene and the anti-bonding carbonyl π* orbitals on the C can undergo a SOI. This helps to stabilise the endo transition state and lower in in energy enough to make it the kinetic product of this cycloaddition. This interaction cannot really be seen in the HOMO of the endo TS as there does not appear to be any electron density present on the carbonyl atom as predicted by SOI. This could be for a number of reasons, one that SOI do not exist or play a dominant role and that the simple theory hides more complex behaviour [10]. Or more likely is that the semi empirical method employed for this situation is not to view the orbital interactions. Perhaps a further investigation with a higher level of theory would help to see if the SOI are there.
Conclusion of investigation
Computational chemistry in this investigation has been demonstrated able to calculate actiovation energies, molecular orbitals, traverse potential energy surfaces from minima to transition structures and from transition structures to minima. All these different techniques when applied properly and with thought can provide useful chemical information. For example in the above experiment the conformers of 1,5-hexadiene which lead to the chair and boat transition state have been elucidated as well as there activation energy. Cycloadditions of butadiene and ethylene have been investigated with a high understanding of it's molecular orbital properties. Stereoselectivity of the cycloaddition of maleic anhydride and cyclohexadiene has also been explained using computational methods. From the above experiments it is clear that computational chemistry has a firm grasp on pericyclic reactions.
A possible improvement to the overall method would be to try and implement statistical mechanics into it. Giving an idea of what conformers are populated thermally and the population numbers. This sort of investigation would help shed more light on the reaction and perhaps allow predictions of what percentage endo and what percentage exo product would be formed from the reactions. Taking computational chemistry into the next level as it would allow it to predict synthetic outcomes.
References
- ↑ http://www.acros.com/
- ↑ E. Brown, R. Bader, and N. Werstiuk, J. Phys. Chem. 2009, 113, 3254
- ↑ http://www.ch.ic.ac.uk/wiki/index.php/Mod:phys3#Appendix_2
- ↑ http://www.ch.imperial.ac.uk/wiki/index.php/Mod:phys3#Appendix_1
- ↑ http://www.ch.imperial.ac.uk/wiki/index.php/Mod:phys3#Appendix_1
- ↑ https://www.ch.imperial.ac.uk/wiki/index.php/Mod:phys3#Results_Table
- ↑ M. Mantina, A. C. Chamberlin, R. Valero, C. J. Cramer, D. G. Truhlar, 1995, 346, pp. 63-69
- ↑ V. Guner, K.S. Khuong, A.G. Leach,, P.S. Lee, M.D. Bartberger, K.N. Houk, J. Phys. Chem. A, 2003, 107, 11445
- ↑ R. Hoffmann, R.B. Woodward, J. Am. Chem. Soc., 1965, 87, 4388
- ↑ J. García, J. Mayoral, and L. Salvatella, Acc. Chem. Res., 2000, 33 , 658