Rep:Mod:usagiphysical

The Cope Rearrangement of 1,5-hexadiene

1,5-hexadiene undergoes [3,3]-sigmatropioc rearrangement reaction as shown in Figure 1. For a long time its actual mechanism was the subject of some controversy and was studied by a large number of experimental and computational researches, but it is recently believed that this reaction is a concerted reaction via either a 'chair' or 'boat' conformation. The transition state with a 'boat' conformation is believed to be higher in energy than that with the 'chair' conformation. The objectives of this exercise are to locate the low-energy minima and transition structures on the 1,5-hexadiene potential energy surface by Gaussian calculation, in order to determine the preferred reaction mechanism.

Figure 1. Cope Rearrangement of 1,5-hexadiene

Optimizing the Reactants and Products

Optimization via HF/3-21G

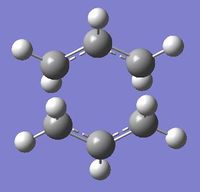
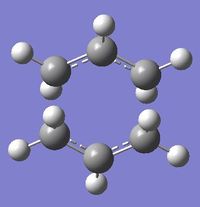
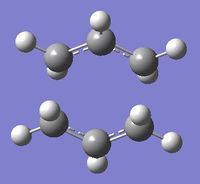
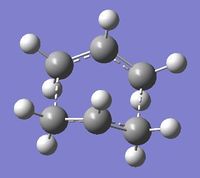
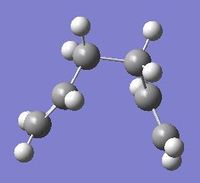
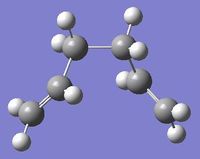
Four conformers (2 with "anti" linkage and 2 with "gauche" linkage) are 1,5-hexadiene were optimized and were confirmed to be anti2, anti4, gauche1 and gauche3 in Appendix 1 by matching the energies.

Table 1.

Name	anti2 (Ci)	anti4 (C1)	gauche1 (C2)	gauche3 (C1)
Structure	anti 2.mol	anti 4.mol	gauche1.mol	gauche3.mol
Calculation Type	FOPT	FOPT	FOPT	FOPT
Calculation Method	RHF	RHF	RHF	RHF
Basis Set	3-21G	3-21G	3-21G	3-21G
Point Group	Ci	C1	C2	C1
Energy/Ha	-231.69254	-231.69097	-231.68772	-231.69266
.log file	File:ANTI2.LOG	File:ANTI4.LOG	File:GAUCHE1.LOG	File:GAUCHE3.LOG

Optimization via B3LYP/6-31G*

The four comformers were then reoptimized at B3LYP/6-31G*.

Table 2.

Name	anti2 (Ci)	anti4 (C1)	gauche1 (C2)	gauche3 (C1)
Structure	anti 2631g.mol	Anti4-631g.mol	Gauche1-631g.mol	Gauche3-631g.mol
Calculation Type	FOPT	FOPT	FOPT	FOPT
Calculation Method	RB3LYP	RB3LYP	RB3LYP	RB3LYP
Basis Set	6-31G*	6-31G*	6-31G*	6-31G*
Point Group	Ci	C1	C2	C1
Energy/Ha	-234.61071	-234.61079	-234.60786	-234.61133
.log file	File:OPTI ANTI 2631G.LOG	File:ANTI4-631G.LOG	File:GAUCHE1-631G.LOG	File:GAUCHE3-631G.LOG

Optimizing at B3LYP/6-31G* level of theory would add polarisation to atoms and improve the modelling of core electrons, producing more accurate description of orbitals as a result.

Summary of Results and Discussion

Table 3 . Optimization and Frequency Calculation Data

Structure	Point Group	Energy 3-21G (Ha)	Energy 6-31G* (Ha)	Sum of electronic and zero-point Energies (Ha)	Sum of electronic and thermal Energies (Ha)	Sum of electronic and thermal Enthalpies (Ha)	Sum of electronic and thermal Free Energies (Ha)
anti2	Ci	-231.69254	-234.61071	-234.41613	-234.40864	-234.407694	-234.45061
anti4	C1	-231.69097	-234.61079	-234.42592	-234.44740	-234.44646	-234.48194
gauche1	C2	-231.68772	-234.60786	-234.46522	-234.45810	-234.45715	-234.49541
gauche3	C1	-231.69266	-234.61133	-234.46869	-234.46146	-234.46052	-234.50011

log files: File:FREQ ANTI 2 631GD.LOG, File:ANTI4-631G FREQ.LOG, File:GAUCHE1-631G FREQ.LOG, File:GAUCHE3-631G FREQ.LOG

Based on the information in the tables above, the HF/3-21G and B3LYP/6-31G* basis set produced conformers with same point group.

The 'anti' conformers were expected to be more stable than the 'gauche' ones because of APP orbital interactions and steric repulsions. πC-C is a higher energy donor than σC-H, therefore the πC-C interacts better with the π*C-C app. Hence APP arrangement of the two vinyl groups is favorable. However unexpectedly the most stable conformer among the four is gauche3, as it is the conformation which possesses the lowest energy. Anti2 is more stable than anti4 and gauche3 is more stable than gauche1 because the two vinyl groups are further apart from each other.

Figure 2. IR spectrum of B3LYP/6-31G* optimized anti2

Geometry Discussion

Figure 3. Anti2 with atoms labelled

Table 4. Bond Lengths & Angles of Anti2

Bond	HF/3-21G (Å )	B3LYP/6-31G* (Å )	Literature	Angle	HF/3-21G	B3LYP/6-31G*	Literature
C1-C2, C5-C6	1.323	1.334	1.3412	C1-C2-C3, C4-C5-C6	124.8	121.8	122.5
C2-C3, C4-C5	1.514	1.504	1.5077	C2-C3-C4, C3-C4-C5	111.3	112.7	111.0
C3-C4	1.548	1.548	1.5362	C3-C2-H	119.7	119.00	118.4
C-H	1.075	1.100	1.108	C2-C3-C4-C5	-179.989	-180.000	-178.3

It could be concluded that B3LYP/6-31G* was more accurate than the HF/3-21G as the bond length and angles were closer to the literature values.

Optimizing the "Chair" and "Boat" Transition Structures

The "Chair" and "Boat" Transition State

An allyl fragment was optimized at 'HF/3-21G(Figure 4), then two of these fragements were used to assemble the "chair" transition state with the terminal ends of the fragments 2.2Å apart (Figure 5). This "chair" structure was then optimised by a various methods i.e. Hessian and Frozen coordinates.

Figure 4. Allyl Fragment

Figure 5. Chair Transition State

For the "boat" transition state, the QST2 method was used. In order to build a "boat" structure, all the atoms of the reactant and the product were numbered as shown in Figure 6.

Figure 6

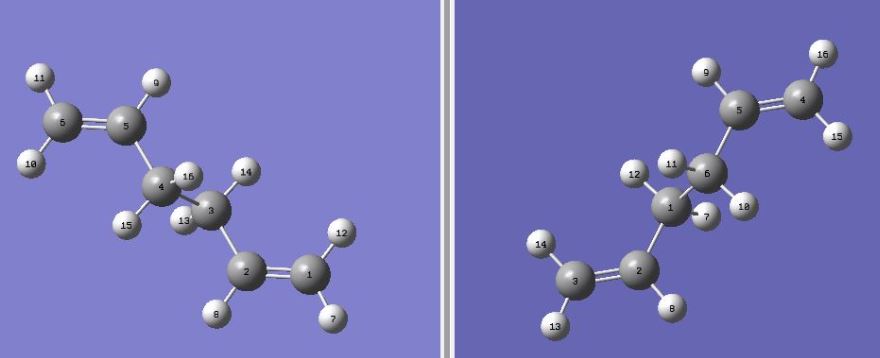
Figure 6

In order to assemble molecules into the desired boat form. The central C-C-C-C dihedral angeles (C2-5 for the reactant, C2-C1-C6-C5 for the product) of both molecules were modified from 180° to 0° and the C-C-C angles (C2-C3-C4 & C3-C4-C5 for the reactant, C2-C1-C6 & C1-C6-C5 for the product) were reduced from 113° to 100°.

Figure 7

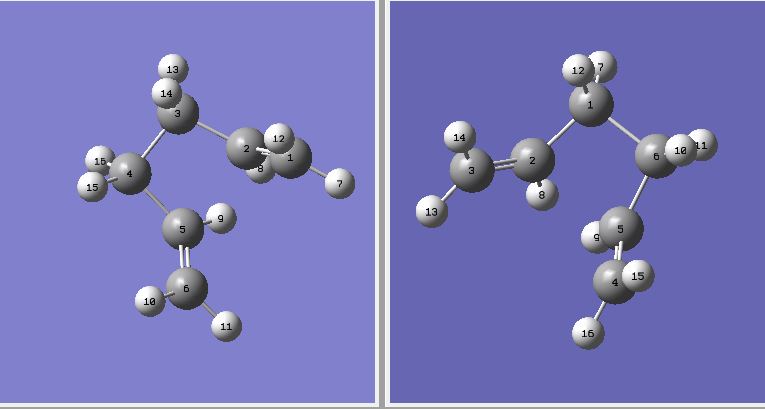
Figure 7 The resultant geometries of the reactant (left) and the product (right) after modification.

These were then optimized at HF/3-21G using the QST2 method. The resultant structure in shown in Table 5.

Table 5 "Chair" and "Boat" Transtion State Optimization

Method	Hessian	Frozen coordinate method (Bond)	Frozen coordinate method (Derivative)	TS (QST2)
Structure	chair	chair	chair	boat
Calculation type	FREQ	FREQ	FREQ	FREQ
Calculation Method	RHF	RHF	RHF	RHF
Basis Set	3-21G	3-21G	3-21G	3-21G
Point Group	C2h	C2h	C2h	C2v
Energy/ a.u.	-231.619322224	-231.61932247	-231.61932246	-231.60280200
Transition bond distances/ Å	2.02039	2.02043	2.02041	2.14000
.log File	File:B)OPT=TS.LOG	File:C) OPT CHAIR FREEZE.LOG	File:D) CHAIR DERIVATIVE.LOG	File:E) OPT FREQ NUMBERING TS BOAT.LOG

***Please click the links provided below to see the original file of Figure 8 and Figure 9 for the animation***

Figure 8. Hessian: Vibration at 817.97cm^-1 (imaginary)Figure 8

As seen from Figure 8, the Hessian method gives an imaginary frequency of 817.97cm^-1 and the vibration mode corresponding to the Cope rearrangement. Both Hessian and the frozen coordinate methods give the tranistion bond lengths of about 2.02Å because of the reasonable assumption of the transition structure. For a molecule which is more complex, it will be more difficult to predict its transition structure by the Hessian method hence the frozen coordinate method would be preferable.

Figure 9 QST2: Vibration at 839.94cm^-1(imaginary)Figure 9

QST2 method gives an imaginary frequency of 839.94cm^-1.

Intrinsic Reaction Coordinate

IRC for the chair transition state was computed on the HF/3-21G basis set, the reaction coordinate was only computed in the forward direction because it is symmetrical. The force constant setting was set to 'calculate always' and the number of points along the IRC is set to 50.

Table 6 IRC

Structure	chair,initial IRC	chair,further IRC from end point
Calculation type	FREQ	FOPT
Calculation Method	RHF	RHF
Basis Set	3-21G	3-21G
Point Group	C2	C2
Dihedral Angle	67.1	64.2
Energy/ a.u.	-231.69121449	-231.69166699
.log File	File:F) CHAIR IRC.LOG	File:F) CHAIR IRC OPT MIN 51.LOG

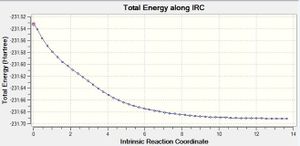
Figure 10. Initial IRC plot

From the structure we got from the initial IRC, it is clear that the transition state has not reached to its minimum as neither its energy nor structure corresponds to any of the conformers listed in Appendix 1. Hence the last point of the initial IRC was optimised to proceed further. The energy of the optimized structure (-231.69166699a.u) matches with the energy of gauche2 in Appendix 1. The IRC method suggests that gauche2 is the conformer of 1,5-hexadiene that leads to the chair transition state structure in the Cope Rearrangement of 1,5-hexadiene.

Reoptimization of Chair and Boat Transition States

The transition states were reoptimized at B3LYP/6-31G*

Table 7 Reoptimize Boat and Chair T.S.

Structure
Calculation type	FREQ	FREQ
Calculation Method	RB3LYP	RB3LYP
Basis Set	6-31G*	6-31G*
Point Group	C2h	C2v
Energy/ a.u.	-234.55698303	-234.54309304
.log File	File:G) CHAIR B3LYP-631G.LOG	File:G) BOAT B3LYP-631G.LOG

Activation Energies

Table 8 Summary of Energies / Ha

	HF/3-21G				HF/6-31G*
	Electronic Energy	Sum of Electronic and Zero-point Energies	Sum of Electronic and Thermal Energies	.log file	Electronic Energy	Sum of Electronic and Zero-point Energies	Sum of Electronic and Thermal Energies	.log file
		at 0 K	at 298.15 K			at 0 K	at 298.15 K
Chair T.S.	-231.619322	-231.466709	-231.461351	File:G) CHAIR HF321 NEWNEW.LOG	-234.556983	-234.414919	-234.408998	File:G) CHAIR B3LYP-631G.LOG
Boat T.S.	-231.602802	-231.450929	-231.445301	File:G) BOAT HF NEW.LOG	-234.543093	-234.402338	-234.396004	File:G) BOAT B3LYP-631G.LOG
Reactant (anti2)	-231.692535	-231.539537	-231.532565	File:OPTI ANTI 2 NEW.LOG	-234.611710	-234.469202	-234.461856	File:G) ANTI2 B3LYP-631G.LOG

• • 1Ha = 627.509 kcal/mol

Summary of Activation Energies / kcal/mol

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.70	44.70	34.07	33.16	33.5 ± 0.5
ΔE (Boat)	55.60	54.76	41.95	41.32	44.7 ± 2.0

The Diels Alder Cycloaddtion

Cis Butadiene

Structure
HOMO	anti-symmetric
LUMO	symmetric
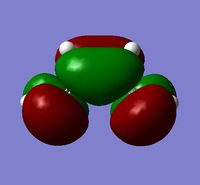Calculation Type	FOPT
Calculation Method	RAM1
Basis Set	ZDO
Point Group	C2V
Energy/Ha	0.04879719
.log file	File:CIS BUTADIENE 1.LOG

The Transition State of prototype reaction between ethylene and butadiene

Figure 11.animation of the butadiene and ethylene cycloaddtion TS File:II)FREQ.LOG