Rep:Mod:ulas
Module 2
Gareth Naylor
Computing the properties of the BH3 molecule
Optimisation
Procedure
The first stage in the optimisation of the BH3 molecule was to learn how to draw the molecule itself. This was done using a range of Gaussian tools and culminated with a BH3 structure with B-H bond lengths of 1.5Ǻ and H-B-H angles of 120°. This structure was now ready for optimisation. This was performed using Gaussian and involved the following properties, all of which could be set in the Gaussian set up menu:
Job Type=Optimisation
Functional=B3LYP
Basis Set=3-21G
It was necessary during these jobs to save the molecule before the job was run. This allowed a number of files to be created under the same name (but different file type) once the job had been completed. In this case the log file was required. This showed a number of interesting results.
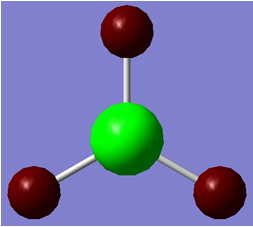
The Gaussian optimised structure of BH3 can be viewed by clicking the following button .
Results
The Gaussian program could be used to compute the values of many properties of the BH3 molecule. One of the most simple pieces of information that can be taken from the program is the B-H bond distance and the H-B-H bond angle of the optimised structure. It turned out that the H-B-H bond angle in the structure stayed identical to the value of before the optimisation, whilst the B-H bond distance shortened considerably to a bond length of 1.19Ǻ. From this it can be concluded that whatever one sets the bond distance to, it will always optimise back to a certain value.
Using the Gaussian summary file it is possible to discover many more properties from the computed structure. The summary file for BH3 is shown in figure 1.
The most important piece of information contained in this file is the RMS gradient, which helps to determine whether or not the optimisation is accurate. It can be seen from figure 1 that the RMS gradient in this case for BH3 is 0.00020672. An accurate value for RMS gradient, which therefore corresponds to a successful optimisation, would be values less than 0.001.
A second method for checking the success of an optimization job is to analyse the output file. In order to show that the optimisation has converged, there should be a yes written next to four different properties. This is best demonstrated in figure 2. Should a file not converge properly then one should check the last few lines of the output file to check for errors.
Gaussview can also be used to analyse the various structures formed in an optimisation. In this case 5 intermediate geometries were found, the last being the optimised structure. These geometries are shown in Table 1. It can be seen from this diagram that bonds only appear in the latter geometries. This can be explained by the fact that in the first three structures the bond length is above a value defined by the program which is considered to be the maximum possible bond length. Therefore it is possible to state that bonds in a program such as this are not dependent on the usual criteria associated with bond formation. It would be expected that the energy of the BH33 molecules would decrease as the structure of the optimised molecule was reached as bond lengths and angles would reach a stable equilibrium. This is best demonstrated by a potential energy curve which shows that as atoms in a diatomic become too close or too far apart energy increases due to the loss and gain of attractive and repulsive forces. This can be proved using the Schrodinger equation. This prediction can be supported by the graph shown in figure 3 which shows the energy dropping with each optimisation step number. The values of energy shown in this graph are given below the intermediate geometries. The graph of how the gradient varies with the optimisation step is shown in figure 4.
 |
 |
 |
 |
 |
|---|---|---|---|---|
| -26.3929a.u. | -26.4182a.u. | -26.4534a.u. | -26.4621a.u. | -26.4628a.u. |
The RMS gradient graph is a particularly good way of proving that an optimisation has occurred as the gradient of the line will hit zero.
Molecular Orbital Analysis
Procedure
The checkpoint (.chk) file from the BH3 optimisation was loaded into Gaussview. A Gaussian calculation was then run using the following criteria:
Job Type=Energy
Functional=B3LYP
'Basis Set=3-21G
The line "pop=full" was then inputed into the additional keywords section, whilst in the NBO tab the "Full NBO" option was selected. This setting analysed the charge distribution within the molecule in order to see how they interact. Check the settings and then submit the job.
Once the job had been run the checkpoint file of the results was opened and the "MOs" option in the edit menu selected.
Results
By selecting occupied from the "visualize" menu it is possible to view all the molecular orbitals of the BH3 molecule. Using these orbitals and the energy given for each MO it is possible to produce a molecular orbital diagram for the formation of BH3 from its component parts, using the LCAO method. This is shown in figure 5.
The molecular orbitals produced using computational techniques can then be compared with the orbitals produced by the LCAO method shown in the MO diagram. The computed molecular orbitals can be viewed in table 2, directly below the MO diagram. Orbitals in this diagram are calculated using the LCAO method.
 |
 |
 |
 |
|---|---|---|---|
 |
 |
 |
 |
Comparing the orbitals produced by the two different methods gives good a correlation. Using the LCAO approximation it can be deduced that there are two sets of degenerate orbitals within the molecule. This is especially interesting in the HOMO region of the MO diagram as this means that there are two orbitals which act as HOMO's. This prediction using the LCAO method can be confirmed by giving the energies of the molecular orbitals produced from computational methods, these energies are shown in table 3. These energies confirm the fact that there are two sets of degenerate orbitals
The main difference in the representations occurs in the fact that the computed MO's show the orbitals blending, which gives a better representation of how the MO would really look. However, when computed molecular orbitals are unavailable the LCAO method has been shown to be a very good approximation.
An advantage of the LCAO method over the computed molecular orbitals is that in the LCAO method it is possible to view the contributions of the atomic orbitals to the molecular orbitals. This makes it easier to identify a molecule from its molecular orbitals. In contrast the computed molecular orbitals are blended and so therefore they could have contributions from any sized atomic orbitals.
It can be seen from the energies of the molecular orbitals that most of the non-degenerate orbitals are fairly far apart in energy. However, this is not the case for the LUMO+1, LUMO+2 and LUMO+3 orbitals which are very close in energy and are often interchangeable. Overall the antibonding orbitals do not correlate well between the LCAO method and the computational method. This is due to the fact that in the degenerate antibonding orbitals there are different numbers of nodes, one has two nodes and one has four, even though the orbitals have the same energy. Realistically, this does not really matter with regard to the BH3 bonding as these antibonding orbitals are never likely to be filled with electrons due to their very high energy.
A further advantage of the computed orbitals is that 15 molecular orbital representations are produced in comparison to the 8 which are produced using the LCAO method, therefore if excited states were to be calculated then use of the LCAO method would not be so useful.
| Molecular Orbital | Energy (a.u.) |
|---|---|
| HOMO-3 | -6.730 |
| HOMO-2 | -0.518 |
| HOMO-1 | -0.357 |
| HOMO | -0.357 |
| LUMO | -0.075 |
| LUMO+1 | -0.189 |
| LUMO+2 | -0.189 |
| LUMO+3 | -0.192 |
Natural Bond Orbital Analysis (NBO)
Procedure
In the case of Natural Bond Order Analysis it is necessary to load the log file obtained from the earlier molecular orbital analysis of the BH3 molecule. From this it should be possible to go the the results tab of Gaussview and select "charge distribution". From this menu select "colour atoms by charge". The "force symmetric charge range" box should already have be checked. A second set of parameters is to check the "show numbers" box instead of the "colour atoms by charge box". These tests give the following results.
Results
When the atoms were coloured by charge, different colours appeared for the boron and the hydrogen atoms. This is best demonstrated in figure 6. A red colour shows a highly negative charge whilst a green colour resembles a highly positive charge. As expected the boron atom holds a positive charge due to the fact that it is highly lewis deficient. A different analysis can take place when a numerical value of the NBO quantities are shown on the molecule. This result is shown in figure 7. This shows that the Boron has a positive charge of 0.332 whilst each hydrogen has a negative charge of -0.111, which explains the slightly red colour shown in figure 6. The charges all add up to zero which shows that the molecule has an overall neutral charge.
Since Gaussview only provides a graphical interface for the molecule it is necessary to analyse the log file. This gave the following results:
Summary of Natural Population Analysis Firstly an analysis of the charges can also be done in the log file in order to check the values given by the graphical version. The results of this analysis are shown in figure 8, which confirms the values given by the graphical version.
Bond Orbital/Coefficents/Hybirds It is then possible to analyse the bonding in the compound by viewing the "Bond Orbital/Coefficients/Hybrids". The part of the input file which details the bonding is shown in figure 9.
This particular part of the input file demonstrates the hybridisation of the molecule particularly well. Thus it is possible to state that the BH3 molecule has an overall sp2 hybridisation as the p contribution is stated to be 66.67% whilst the s contribution is quoted as being 33%. This data also shows how in the B-H bonds the Boron contributes 55.52% of the electron density, whilst the Hydrogen contributes 44.48% of the electron density to the bond.
Second Order Perturbation Theory
The Second Order Perturbation Theory part of the input analyses the Fock Matrix in the NBO basis. This is shown in figure 10.
Natural Bond Order Summary
Finally the natural bond order can be analysed in order to convert molecular orbitals back into 2 electron bonds and lone pairs. This analysis is shown in figure 11.
The first three data entries in this summary represent the atomic orbitals involved in the molecule and hence have occupancies very close to 2. This corresponds to having two electrons. The fourth entry in this data also has an occupancy of 2. In this case a lone pair is the origin of these electrons. It is also interesting to analyse the energies of the orbitals. It can be seen that all of the first four orbitals have negative energies, however the lone pair in particular has a very negative energy. This shows that all these orbitals stabilise the molecule. The fact that most of the other orbitals have positive energies suggests that if electrons were placed in the orbital they would destabilise the molecule.
Frequencies
Procedure
Firstly open the log file from the BH3 optimisation. Rename this file and then run a frequency calculation on it using the following criteria:
job type = frequency additional keywords = "pop=full nbo" functional=B3lyp basis set=3-21g
Give the job a title and then submit it to the Gaussian interface. When the job has finished open the log file and check in the summary that the job has completed successfully. This can be tested by checking that the energy is similar to that given by the optimisation (first four decimal places must be the same). Some other parts of the log file can then be used to take results from this frequency calculation.
Results
Using the log file the low frequencies of the molecule can be analysed. These are shown below in figure 12.
The frequencies shown in figure 12 correspond to those of the centre of mass of the molecule. These frequencies are over an order of magnitude higher than the standard for zero frequencies. This shows that the method used for this calculation is very low-level as the better the method is the closer to zero the frequencies become.
In order to check that the frequencies for this molecule have been calculated properly it is necessary to check for any negative frequencies. If all the frequencies are positive then it implies that the calculation has been successful. This is because the frequencies are calculated by taking the second derivative of the potential energy surface. If the value is positive then this is indicative of a minima, whilst a negative value is indicative of a maxima, ie a transition state. The frequencies and the associated animations for BH3 are shown below in table 3.
| Vibrational Mode | Animation | Frequency cm -1 | Intensity | Symmetry D3h point group | Description |
|---|---|---|---|---|---|
| 1 |  |
1145.7 | 92.7 | A2' | Hydrogens move in opposite directions to Boron. Occurs perpendicular to σh plane. |
| 2 |  |
1204.7 | 12.4 | E' | Scissoring motion of two hydrogens towards each other in σh plane. |
| 3 |  |
1204.7 | 12.4 | E' | Known as a rocking motion, in which two hydrogens are scissoring and one is rocking |
| 4 |  |
2592.79 | 0.00 | A1' | Hydrogens move in a symmetrical fashion away from Boron |
| 5 |  |
2731.3 | 103.8 | E' | Hydrogens move in an asymmetrical fashion away from boron |
| 6 |  |
2731.31 | 103.8 | E' | known as an anti-asymmetric stretch in which two hydrogens move in a symmetrical fashion away from Boron whilst the other moves in an asymmetric fashion. |
It is then possible to show these vibrations in the form of an IR spectrum. This spectrum is shown in figure 13.
The spectrum shown in figure 13 has only three peaks, even though there are the expected six vibrations given by Gaussview (taken from the 3N-6 equation for non-linear molecules). This can simply explained by the fact that vibrational mode 4 has no overall dipole moment, therefore giving an intensity of 0 and will not show up on the infra-red spectrum. There are also two sets of degenerate peaks, meaning that only one peak will show on the spectrum.
Thalium Bromide
Procedures
As with BH3, TlBr3 was drawn in GaussView. On this occasion the point group of the molecule was set to D3h (high tolerance) in order to keep the symmetry, as this reduces the optimisation times. The molecule was then optimised using the following criteria:
Functional: B3lyp
Basis set: LANL2DZ
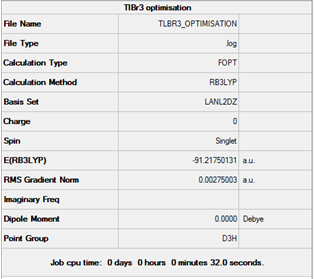
This specific basis set was used as it includes pseudo potentials, which compensate for larger heavier atoms as it only takes into account the electrons taking part in the bonding rather than each electron in turn. This is because of the fact that for heavier atoms taking each electron into account would prove extremely time consuming, so only the valence electrons are considered. The summary file for this optimisation is shown in figure 14.
Results
From the optimised molecule a number of properties can be deduced. These include the Tl-Br bond distance (2.65095 Angstroms) and the Br-Tl-Br bond angle (120o). This value was quite close to the literature value for bond length (2.52 Angstroms)[1]
Frequencies
Media:gn08.TlBr3.freq.txt As for the BH3 molecule the vibrational frequencies can be computed, which are useful for checking whether or not the molecule has been optimised to a minimum. The part of the log file which shows the low frequencies is shown in figure 15.
These values can then be shown in the form of a spectrum, which can be compared with the spectrum for BH3 in order to deduce whether or not the basis set used has an effect on the vibrational frequencies. The spectrum showing these frequencies is shown in figure 16.
As with the BH3 molecule the TlBr3 molecule has six vibrational modes, which conforms to the 3N-6 rule for number of vibrational modes. It was stated for BH3 molecule that the low frequencies, which are meant to be as close to zero as possible, are actually very high as the basis set is used is particularly low level. On the other hand, in the case of TlBr3 the basis set used is much more accurate, meaning that the values of the ‘low frequencies’ are closer to zero. This confirms that the basis set used in this part of the investigation is more accurate than that used for BH3. Again the spectrum shows only 3 peaks. This is for the same reason as the BH3 molecule ie because of a totally symmetrical vibration (which confirms we have optimised the molecule) and due to degenerate peaks.
Sometimes bonds are not shown when viewing optimised molecules in the Gaussview program. This is due to the fact that the program has a specific distance that a bond should be. Therefore, if the difference between two atoms is greater than this bond distance specified on the program then a bond will not be inserted. This is a particular problem for inorganic molecules as bond distances tend to be longer.
A bond can formally be defined as interactions between atoms, which can be of many different types, for example covalent or dipole-dipole interactions. Whether or not a bond exists should not depend on the distance involved but more to do with whether interactions are present.
Isomers of Mo(CO)4L2
In the next part of the investigation isomers will be analysed with respect to the number of stretches that the carbonyl groups show. The number of stretches that the carbonyl groups show depends on the symmetry of the molecule. Therefore a pair of cis- and trans- isomers should give differing IR spectra, therefore giving a means of differentiating between the two structures. In this section the isomers will be compared in terms of their energies and their IR spectra, in order to determine the most stable isomer and confirm predictions in relations to the vibrational spectrum.
Procedure
In this part of the module the L ligands used were Cl as they are less computationally demanding than the standard phenol ligands, therefore meaning that the computations run faster. It was first necessary to perform an initial rough optimisation on both the cis- and trans- structures. This was done using the following criteria:
Functional = B3LYP
Basis Set= LANL2MB
Additional Keywords = opt=loose
The basis set used in this optimisation was low level due to the rough level of the optimisation. Once this initial calculation was completed, a second optimisation was carried out on the molecules. Before this calculation was carried out, a number of adjustments were made to the structures, in order to try to reduce the energy further. The PCl3 groups in the trans structure were made eclipsed whilst in the cis- structure one P-Cl bond was positioned axial to an Mo-C=O bond. On the other PCl3 group it was ensured that one P-Cl bond was pointing down and away from the other PCl3 group. This gave torsion angles of 0 degrees for the synperiplanar bond and 180 degrees for the antiperiplanar bond. The second optimisation was then done using the following criteria:
Functional: B3LYP
Basis set: LANL2DZ
Additional Key words: int=ultrafine scf=conver=9
This criteria represents a much tighter calculation giving a more accurate structure.
Finally a frequency calculation was carried out on each structure in order to analyse the low frequencies of the structures. This was done in a very similar manner to above using the LANL2DZ basis set and maintaining int=ultrafine scf=conver=9 as the keywords. This is done to avoid having any negative frequencies.
Results
The structures and summaries for both sets of optimisations are shown below in figures 17, 18, 19 and 20.
Optimisation 1:
Cis- DOI:10042/to-7699
Trans- DOI:10042/to-7698
Optimisation 2:
Cis-
Trans- DOI:10042/to-7683
From these summary images it is possible to see that the second optimization lowers the energy by around 6.1a.u. both the cis and the trans- cases. It can also be deduced from the summary files that the trans- isomer is more stable than the cis- isomer.
Using the optimised structures the properties of both the cis- and trans- isomers can also be found. These properties are shown in table 5 shown below.
| trans | cis | |
|---|---|---|
| Mo-P bod length (angstroms) | 2.44 | 2.51 |
| P-Mo-P bond angle (degrees) | 177.4 | 94.2 |
Frequencies
cis:DOI:10042/to-7702 trans:DOI:10042/to-7701 Initially, the frequency calculations were checked for minima value in order to make sure that minima had been found. The results of this analysis showed that all values were in fact positive. The key vibrational modes of the low frequency stretches for both the cis- and the trans- isomers were then tabulated in tables 6 and 7.
| Vibrational Mode | Animation | Frequency cm -1 | Intensity | |
|---|---|---|---|---|
| 1 |  |
10.75 | 0.0264 | |
| 2 |  |
17.64 | 0.0074 |
| Vibrational Mode | Animation | Frequency cm -1 | Intensity | |
|---|---|---|---|---|
| 1 |  |
4.9 | 0.0937 | |
| 2 |  |
5.96 | 0.0006 |
Next the carbonyl stretching frequencies of the two isomers were compared with those in the literature. This comparison is shown in tables 8 and 9:
| Frequency | Intensity | description |
|---|---|---|
| 1950.34 | 1475.4 | Two trans- carbonyls stretching asymmetrically |
| 1950.97 | 1466.8 | the other two trans- carbonyl groups stretching asymmetrically |
| 1977.25 | 0.6 | All four carbonyl groups stretching asymmetrically |
| 2031.03 | 3.8 | All four carbonyl groups stretching symmetrically |
| Frequency | Intensity | description |
|---|---|---|
| 1945.29 | 762.9 | Two cis- carbonyls stretching asymmetrically |
| 1948.66 | 1498.3 | Two trans- carbonyl groups stretching asymmetrically |
| 1958.35 | 632.8 | All four carbonyl groups stretching asymmetrically |
| 2023.30 | 597.7 | All four carbonyl groups stretching symmetrically |
Each of the isomers show four carbonyl peaks which correspond to different stretches of the molecule.
The IR spectra for the cis- and the trans- isomers are shown in figures 20 and 21:
Mini Project
This mini project will investigate tri-substituted group V complexes. The initial focus will be on trisilylamine, however as the project goes on this will be extended to include central atoms further down group V such as Phosphorous and Arsenic, in order to investigate the effects of including d-orbitals in the calculations. One of the main avenues of investigation will be to explore why the trisilylphosphorous compound has a pyramidal structure compared to the planer structure that the trisilylamine adopts. This investigation will the be extended to the As molecule in order to investigate which structure it adopts This will include undertaking a range of computational techniques including the use of pseudo-potentials to take into account the use of the heavier elements such as As. Many of the techniques already used in the above parts will then be utilised again in order to analyse the molecules produced.
Optimisation
N(SiH3)3 1st optimisation: DOI:10042/to-7879 P(SiH3)3 1st optimisation: DOI:10042/to-7878 N(SiH3)3 2nd optimisation: DOI:10042/to-7880 P(SiH3)3 2nd optimisation: DOI:10042/to-7881 Optimisations on the molecules involved in this investigation can be split into two categories; those which use pseudo-potentials and those which do not. The first set to be considered were those that do not contain pseudo-potentials, ie those with lighter elements. In this case both 2 optimisations took place using the same keywords as specified in the stereoisomer investigation above. However, in this case the basis set used was 6-31g(d,p). The optimised structures and summary files for both the N(SiH3)3 and the P(SiH3)3 for both optimisations are shown in figures 22, 23, 24 and 25.
N(SiH3)3
Optimisation 1:
Optimisation 2:
P(SiH3)3
Optimisation 1:
Optimisation 2:
In the case of phosphorous the literature[2] states that the structure is pyramidal, compared to the planar structure adopted by the trisilylamine. It was therefore investigated whether or not inputing a planar P(SiH3)3 would optimise to the pyramidal structure. The results of this investigation was that the planar structure would always optimise to the pyramidal structure. Therefore it was only necessary to optimise the planar structure.
It can be seen from the summary files that performing the second optimisation does not have much effect on the energy values. However, it can be confirmed that the optimisation has been completed by checking the low frequencies of the molecule, in order to check that there are no maxima present. The low frequencies of these molecules, taken from the log files are shown in figure 26.
These do show negative frequencies corresponding to transition states, however looking at the log files (shown above) it can be seen that the optimisations have converged properly. This means that there must have been an inaccuracy in the basis set which gave negative frequencies.
Optimisation of heavier molecules using pseudo-potentials As in the optimisation of the TlBr3 molecule it was necessary to use pseudo potentials to optimise the As(SiH3)3 molecule.DOI:10042/to-7890 This was done using the LANL08d basis set taken from the EMSL Basis set exchange.
Molecular orbital analysis
N(SiH3)3: DOI:10042/to-7889 N(SiH3)3: DOI:10042/to-7886 One likely way of rationalising the structures of these compounds is to carry out a molecular orbital analysis. Since phosphorous is further down group V than nitrogen it would be expected that there would be more molecular orbitals involved, due to the fact that it has electrons occupying the 3s and 3p orbitals, as welll as having unoccupied available d-orbitals. In reality, the results of these computations show that the phosphorpus compound has only four additional molecular orbitals than the nitrogen compound. Approximate energy level diagrams for both complexes, which include details of which orbitals are occupied are shown in figure 27.
From this energy level diagram it is clear to see that the phosphorous compound has many more occupied molecular orbital than the nitrogen compound. This is due to the fact that it contains electrons in the 2p and 3s orbitals which are then able to mix with the SiH3 orbitals to give a greater number of occupied MO's.
Next the valence MO's of the compounds can be compared in order to see if they can explain the differences in structures of the complexes. The HOMO's of both the nitrogen and the phosphorous compounds are shown in figures 28 and 29 These show that phosphorous has a large amount of electron density on the unbonded face of the atom. This is representative of a lone pair on the phosphorous, which will repel with the bonding electrons, shown by the other areas of electron density, giving the pyramidal structure. The nitrogen complex, on the other hand, has a HOMO which is symmetrical in the plane, and does not have a superior amount of electron density on either the top or the bottom face.
Natural Bond Orbital (NBO) analysis
The presence of a lone pair of electrons on the phosphorous complex can be checked by carrying out an NBO analysis. This was done using the same procedure as in earlier exercises.
Both the coloured and the numerical NBO representations are shown below in table 10.
| N(SiH3)3 molecule | P(SiH3)3 molecule | |
|---|---|---|
| Coloured representation |  |
 |
| Numerical representation |  |
 |
These representations are not very helpful to the investigation as it is very difficult to distinguish between the colours of the phosphorous and the nitrogen. It is also very difficult to use the numerical data as the magnitudes of the charges given are very different.
It is also possible to use the natural bond order summary to check on the influence of lone pairs in a molecule. This is shown for both the nitrogen and phosphorous compounds in figure 30.
From these values it can be seen that the nitrogen lone pair has less influence on its molecule than the phosphorous lone pair which is almost equivalent to a bonding pair. This can be seen from the occupancy value in each set of data.
Analysis of Structural properties
It can be seen from the optimised structure of the nitrogen compound that Gaussview has attributed it with a higher bond order than the pyramidal phosphorous structure. From these optimised structures it is possible to take the values of the bond lengths and angles for all three molecules, in order to determine whether or not this higher bond order is justified. The results of this analysis are shown in table 11.
| N(SiH3)3 molecule | P(SiH3)3 molecule | |
|---|---|---|
| Bond Length (Angstroms) | 1.75 | 2.26 |
| Literature Bond Length (Angstroms) | 1.73 | 2.25 |
| Bond Angle (degrees) | 120 | 99.9 |
The most interesting information that can be deduced from the properties is that the P-Si bond length is significantly longer than the N-Si bond length. This is mainly due to the fact that phosphorous is a much bigger atom that nitrogen and so therefore the nuclei are further apart. These bond internuclear distances also explain why the nitrogen compound has been attributed a bond order of 1.5 compared to the phosphorous compound which is only attributed a bond order of 1. These values of bond length compare extremely well to those given in the literature[3] as they are within 0.1 or 0.2 angstroms.
===Literature Analysis===[4]
The literature contains an interesting argument with regard to the origin of why N(SiH3)SiH3 is planar. It is claimed that the strengthening of the N-Si bond is due to n(N)-->σ*(Si-H) electron donation. This corresponds to the nitrogen lone pair donating into the antibonding orbital of the Si-Hydrogen bond. This is known in the literature as negative hyper-conjugation. This explains why the nitrogen lone pair does not affect the bond angle as it does in the phosphorous compound. A second reason for the adoption of the planar structure is related to the SiH3 groups experiencing long range electrostatic interactions. The SiH3 groups are further apart if they are in a planar structure which therefore means that this is a much more favourable structure. These interactions will not be present in the phosphorous compound as the P-Si bond length will be sufficiently long enough so that these interaction will not take place.
Conclusion
In conclusion, it was difficult to prove from many of these investigations exactly what the literature stated with regards to the structure of the trisilylamine and corresponding phosphorous compound. If it were possible to further the investigation one should investigate the corresponding As compound. However, from the investigations carried out in the rest of this mini project and following the trend that is apparent from the literature, one would predict that the As compound would adopt a trigonal planar strcuture. This would be due to the fact that its bond lengths would be even longer than those from the phosphorous compound.
references
- ↑ J. Blixt, J. Glaser, J. Mink, I. Persson, P. Persson and M. Sandtroem, J. Am. Chem. Soc., 1995, 117 (18), p 5094
- ↑ C. E. Housecroft, A. G. Sharpe. Inorganic Chemistry, Third Edition, Pearson Education Limited, 2008 p398-399
- ↑ C. E. Housecroft, A. G. Sharpe. Inorganic Chemistry, Third Edition, Pearson Education Limited, 2008 p398-399
- ↑ C. E. Housecroft, A. G. Sharpe. Inorganic Chemistry, Third Edition, Pearson Education Limited, 2008 p398-399