Rep:Mod:tyy15 y3TS
Transition States and Reactivity
Introduction
Locating and examining the transition state has always been challenging in the field of chemistry before computational methods are developed. Since transition states are very short-lived, using experimental techniques in the laboratory to determine the structure of the transition state has proven to be very difficult or nearly impossible. Hammond's Postulate has helped scientist to give first approximation on what the transition might look like, by stating that the transition state structure will closely resemble the structure of product or reactant depending on which one is closer in energy with the transition state. The emergence and development of computational chemistry has not only helped to locate the transition state and provide you with the structure of the transition state, it can also be used to calculate the relative energy of reactants, T.S, and product in order to comparison between experimental data obtained in lab. Better understanding of the mechanism of the reaction can be brought about through knowing the transition state.
Transition state can be considered as the highest energy state within the reaction coordinate. Transition state will have a gradient of zero with a negative second derivative on the curve. The reaction coordinate we usually plot represents varying only one degree of freedom while keeping other degrees of freedom in equilibrium. An equilibrium mode would mean that those modes are kept in their lowest energy state, such that these structures (those not shown on the reaction coordinate) are said to be minimised. Minimised structure can be found on the PES, such that they will have value of zero for the first derivative, and a positive value for the second derivative. A saddle point is then said to be located. A useful reaction coordinate requires knowing which degree of freedom to vary depending on which degree.
Nf710 (talk) 22:32, 7 March 2018 (UTC) This is correct but you need to be working in 3N-6 degrees of freedom. You get the second derivatives of these by diagonalising the hessian matrix. the eiegen vectors are the normal modes (vibrations)
In this exercise conducted below, we will explore a few Diels-Alder reactions and try to examine and analyse the Transition State, Potential Energy Surface and MOs of these structures. The reactions are run using Gaussview and each of the structure presented below are optimised by either the semi-empirical PM6 method or the Density Functional Theory method using B3LYP/6-31G(d) basis set. The molecules are drawn and optimised in Gaussview, by calculating the potential energy of all degrees of freedom of the molecule. The degrees of freedom are represented as various normal vibrational modes in each molecule. Linear molecules will possess (3N-5) vibrational modes and non-linear molecules will possess (3N-6) vibrational modes. N is representing the number of atoms in the molecule.
The program uses quantum chemistry to examine the wavefunction of each of the molecule. In each case, the Schrodinger equation is solved by using LCAO method. The overall wavefunction is the sum of individual degrees of freedom added together. Since there are so many degrees of freedom, a Hessian matrix can be employed to evaluate this complex Schrodinger equation. This will provide a solution for the Schrodinger equation. Then, the program will evaluate the energy of the system by applying the Hamiltonian operator to the Schrodinger equation.
Nf710 (talk) 22:32, 7 March 2018 (UTC) You are getting mixed up between the hessian and the hamiltonian. the hessian is matrix of second derivatives and is used for evaluating the PES and its stationary points. The hamiltoinian is used to calculate the Schrodinger equation.
The two methods that we use to optimise our structures and calculate energies represent the different ways in solving the Hessian matrix as discussed above. The PM6 method is a semi-empirical method, which stands for parameterization method 6. This method examines the Hessian matrix by correlating the functions to experimental data in the program. Therefore, it doesn't calculate all the values in the matrix, but it uses empirical values that speeds up the calculation. This is therefore called a semi-empirical method and the calculation does not that that long. For the other method that we use, it was the Density Functional Theory (DFT) method which uses the B3LYP/6-31G(d) basis set. This method again evaluates the Hessian Matrix, by calculating the electron density of each term in the matrix. The B3LYP/6-31G(d) basis set gives a hybrid function which correlates the energy calculated by DFT to the Hartree-Fork theory. The calculations are done from first principle, meaning that it will take a longer time for the calculations to run. It makes sense that our B3LYP calculations are done on the optimised structure from PM6 method, which should speed up the calculation by not starting from scratch. The IRC calculation that we ran represents the intrinsic reaction coordinate. It locates the minimum pathway on the potential energy surface between two minima. This is found through displacing our structure at the highest energy point in both directions, which is our transition state, and calculating the minimum energy pathway. Transition state will have a first derivative of zero and a negative second derivative. This leads to one imaginary (negative) frequency being able to be observed at the transition state. Other minima will have a positive second derivative at the minima, hence will not show a negative frequency of vibrations and would help us to distinguish between reactants/products and transition states.
Nf710 (talk) 22:32, 7 March 2018 (UTC) Good understanding of the quantum methods. Nf710 (talk) 22:32, 7 March 2018 (UTC) This sections was good but it could have been written hugely more concisely. with some picture or so equations to break up the text. You also got a bit confused at points.
Exercise 1
(Fv611 (talk) Excellent work and discussion throughout the whole section. However, you should have labelled the TS MOs consistently across the table and the MO diagram.)
In this exercise, we have explored the [4+2] cycloaddition reaction between butadiene and ethylene. It can also be classified as a Diel-Alder reaction. Its reaction scheme can be found below in Figure.1. Analyses were conducted to explore the transition state, in relation to the reactants and the products. All the reactants, transition states, and the product was optimised using the PM6 method.
Molecular Orbital Diagram
The energy of the different MO of the reactants and transition state was calculated using the optimised structures and their values can be compared. A MO diagram was constructed to probe the relative energy levels of the transition state, in comparison to the two reactants: ethylene and butadiene. The MO diagram can be found below in Figure.2.
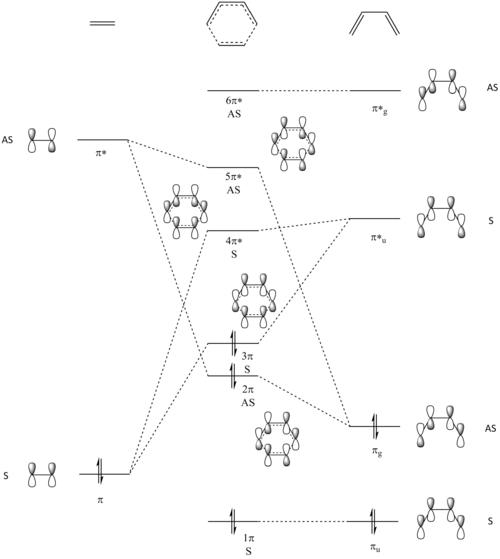
The HOMO and LUMO of the two reactants are the MOs that would participate in bonding in this reaction. They are displayed here as Jmol objects, helping us to understand the geometry of the orbitals and how they can participate in bonding. Each of the two reactants has its corresponding HOMO and LUMO and can be found here. These four original individual MOs will linearly combine and give four MOs for the transition state. The interaction between these orbitals can be seen in our MO diagram in Figure.2 as well as a Jmol file from our calculation here.
We can see from the calculation that the resulting MOs from the transition state consists of two bonding orbitals as well as two anti-bonding orbitals. It is seen that the two antisymmetric MOs of the reactants combined to give two antisymmetric MOs in the transition state, namely the 2π and the 5π*orbitals. Conversely, the two symmetric MOs of the reactants combined to give two symmetric MOs in the transition state, namely the 3π and the 4π* orbital. Through this, we can conclude that the same symmetry between the two fragments is required to be the same in order for a linear combination of the MOs to occur. This suggests that the orbital overlap integral will be zero for a symmetric-antisymmetric combination as confirmed by the non-interacting nature of these orbitals. In the case of symmetric-symmetric interaction and antisymmetric-antisymmetric interaction between the orbitals, the orbital overlap integral will be non-zero as found from the linear combinations between these orbital leading to the formation of the transition state. Therefore, it can be determined that the reaction is allowed when the MOs of same symmetry combine while the reaction is disallowed when the MOs of different symmetry is combined. This gives rise to the selection rule when different MOs interact together.
Bond Length Analysis
Bond length analysis was also conducted for the reactants, transition state and the product to probe its changes throughout the reaction. The result can be found in Figure.3 below. These values can then be compared to Table.1 below, which includes the literature values of typical sp3 and sp2 bond lengths as well as Van der Waals radius of C atom.

| Csp3-Csp3 (single bond) [1] | Csp2=Csp2 (double bond)[2] | Van der Waals Radius of C atom [3] | |
|---|---|---|---|
| Bond Length / Å | 1.54 | 1.34 | 1.77 |
A change in bond length between the carbon atoms can be observed throughout the reaction. A noticeable change can be observed between C1 and C2. These two atoms are the two carbons from the original ethylene, which has a double C-C sp2 bond between them and has a bond length of 1.33Å. However, during transition state, the bond length has increased to 1.38 Å, which can be explained by the formation of a partial double bond instead of a full double bond between C1 and C2. This value agrees with literature, which is a bond length between C-C sp3 and C-C sp2.This bond further increases the bond length to 1.53 Å, which suggest the formation of single C-C sp3 bond when compared to literature. Similar observation can be found between C3-C4 and C5-C6, which the double bond from reactant is turned into single bond in the product.
An opposite effect is seen between C4 and C5, where the single bond is turned into a double bond from reactants to product. The bond length changes from 1.47 Å to 1.34 Å which suggests the change from C-C sp3 bond to C-C sp2 bond. These values also agree closely with the literature values presented in Table.1.
Another interesting result that was obtained was the newly formed bonds between C2 and C3, as well as C6 and C1, during the reaction. We would expect that the distance of C2-C3 and C6-C1 will be slightly shorter than twice of the Van der Waals radius of carbon. This is because we have established in the previous section (See Molecular Orbital Diagram above) that there are interactions between the MOs of ethylene and butadiene during the transition state. This would mean that the MOs will overlap and hence leading to a shorter bond between the carbons. This is confirmed by the results we obtained, which bond lengths of 2.11 Å were found for these two bonds and is smaller than 3.4 Å (twice of Van der Waals radius).
Vibrational Analysis
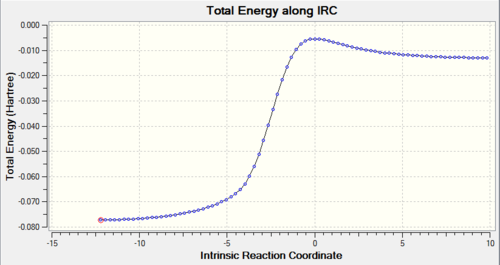
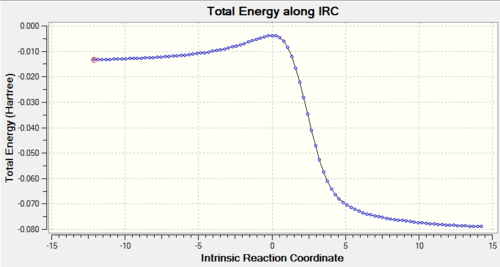
The IRC and the vibrational frequencies were also probed in this exercise. During the transition state, an imaginative(negative) frequency should be found since a saddle point that contains a negative second derivative is situated at the point. The imaginative frequency found was - 948.74 cm -1. Both IRC and imaginary frequency can be found below in GIF.1 and GIF.2. Through this computational stimulation, we observe that the ethylene approaches the butadiene in a synchronous and concerted fashion during the transition state, leading to the bond formation.
| IRC | Imaginary Frequency at The Transition State |
|---|---|
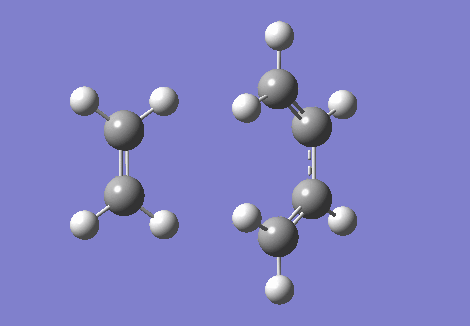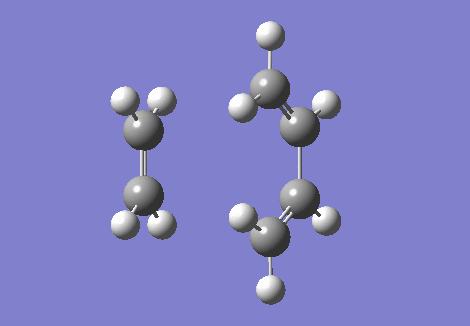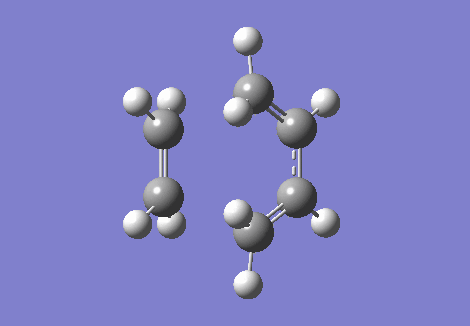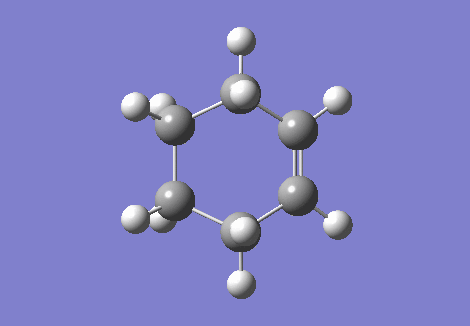 |
 |
Exercise 2
In this exercise, we have explored the Diels-Alder reaction between cyclohexadiene and 1,3-dioxole. We will determine whether this Diels-Alder reaction is a normal or inverse electron demand reaction. Both the exothermic and endothermic product were probed and their results were compared. The reactants, transition states, and products were first optimised using the PM6 method, followed by the B3LYP/6-31G(d) method. IRC and frequency calculations were conducted for the transition states. The reaction scheme can be found below in Figure. 4.
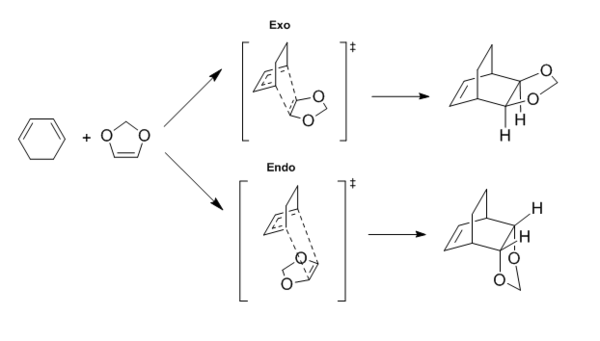
Molecular Orbital Diagram
(Fv611 (talk) Very good MO diagrams. Well done!)
MO diagrams were constructed for both the exothermic and endothermic transition state. They are put next to each other for ease of comparison. This can be found below in Figure.5.
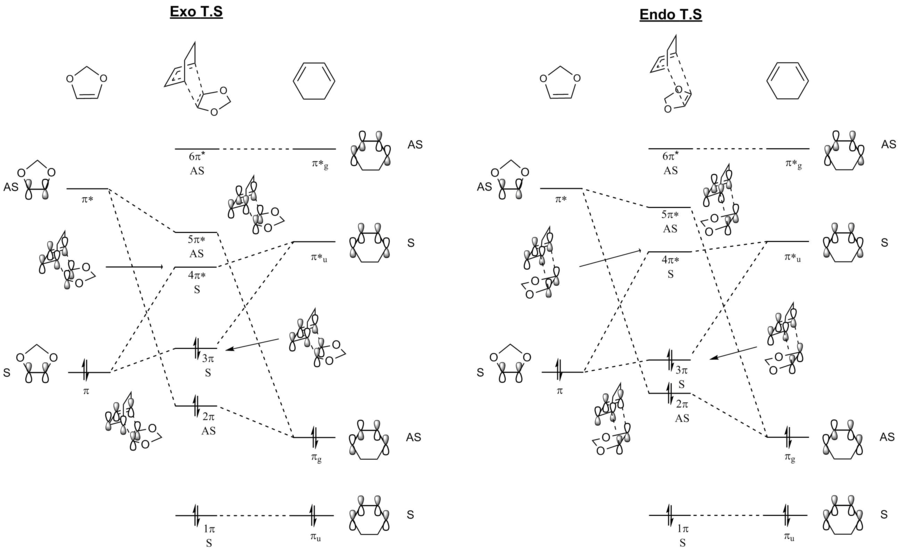
The HOMO and LUMO of the transition state of the exothermic and endothermic product can be found here and here respectively as Jmol files. Using the theories established above from exercise 1, we again see that linear combination between MOs with the same symmetry has resulted in a non-zero orbital integral overlap.
The HOMO and LUMO for both exothermic and endothermic transition state were symmetric in nature and were formed by the interaction between the symmetric π orbital of the 1,3-dioxole fragment and the π*u fragment of the cyclohexadiene. Their interaction forms the 3π HOMO and the 4π* LUMO in the resulting transition states.
By running a single point energy calculation on the reactants geometry on the IRC calculations, we can calculate the energy of the different orbitals, hence able to determine their relative energy level on the MO diagram on Figure.5. From the results obtained, we have found that the formation of the HOMO and LUMO of the transition state is from the interaction between HOMO of the dienophile, 1,3-dioxole, and the LUMO of the diene, cyclohexadiene. This shows that the reaction is an inverse electron demand Diels-Alder Reaction, as the diene LUMO has a higher energy than the dienophile HOMO. The Diels-Alder reaction is between an electron-rich dienophile and an electro-poor diene. The two oxygen atoms on the 1,3-dioxole are electron donating in nature, leading to the interaction between LUMO of cyclohexadiene and HOMO of 1,3-dioxole. These two orbitals have energy levels that are closer in energy than the LUMO of 1,3-dioxole and HOMO or cyclohexadiene.
The energy of the HOMO and LUMO of the endothermic and exothermic transition states were also examined. Their relative energies were placed on the MO diagram according to the calculation. It can be seen that the HOMO-LUMO gap for the exothermic reaction is smaller as compared to the endothermic reaction. When examining the transition state, the HOMO of the endothermic transition state will be at lower energy as compared to the HOMO of the exothermic transition state. This is because, in an endothermic transition state, the p-orbitals of the oxygen on 1,3-dioxole will interact and overlap with the p-orbital of the cyclohexadiene. This in turns means that the HOMO of the transition is lowered and the LUMO is raised, leading to a larger HOMO-LUMO gap for the endothermic reaction.
Nf710 (talk) 22:36, 7 March 2018 (UTC) Well done for doing this but it would have been nice if you could have put the data in a table rather than just stating it.
Activation and Reaction Energies
Calculation regarding the activation energies and the reaction energies was done and recorded in Table.2 below. The energy of reactants, transition states, and products was extracted from their optimised structure using method described above. The reactants energies were calculated by summing the two individual reacts together, assuming that they are placed at infinite distances before the reaction occur and hence no interaction was made possible. To visualise the reaction better, a reaction coordinate was drawn below a well in Figure.6.
For this Diels-Alder reaction, we would expect the endothermic product to the kinetic product. This is because transition state is stabilised by the p orbital overlap between the oxygen atoms on the 1,3-dioxole and the diene of cyclohexadiene. This is both supported by the Jmol files uploaded above and also the MO diagrams above. The endothermic pathway has a lower activation energy, hence it is classified as the kinetic product. For the exothermic reaction, no secondary orbital interaction is observed as the p orbital of the oxygen atoms are no longer below the diene p orbital. This means that the transition state cannot be stabilised. This effect is shown in Figure.7.
In a typical Diels-Alder reaction, the exothermic product is supposed to be the thermodynamic product as the endothermic product is susceptible to experience 1,3-diaxial interaction, which disfavours its formation. Placing the substituents on the equatorial position, such that in the exothermic product, should help to relieve the apparent repulsion experience in the endothermic product. However, the energy that was calculated suggests otherwise. The endothermic product is also the thermodynamic product as suggested by data as it as a lower reaction energy. This can be explained by the steric clash that might be experienced by the exothermic product, which the hydrogen on dioxole ring is sterically clashing with the bridging hydrogen as depicted in Figure.7. This destabilises the exothermic product and raises its energy. The endothermic product is therefore both the kinetic and thermodynamic product.

Nf710 (talk) 22:38, 7 March 2018 (UTC) This section was well written. Your energies are correct and you have come to the correct conclusions. However you could have gone into more detail about the electron demand of the reaction and also the kenetic theory behind the reaction.
Exercise 3
In this exercise, two kinds of reactions were probed by reacting O-xylylene and SO2. A hetero Diels-Alder reaction was examined to probe the endothermic and exothermic products. The other reaction that was probed was the cheletropic reaction. The reaction scheme is shown below in Figure.8. It can be seen that a Diels-Alder reaction will yield a 6-membered ring while a cheletropic reaction will yield a 5 membered ring. All the reactants, transition states, and products were optimised using the semi-empirical PM6 method. IRC calculations were conducted for all three transition states.
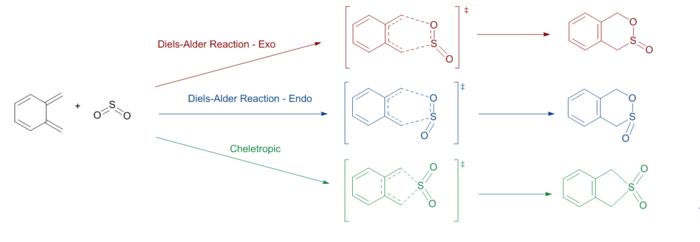
IRC Calculations
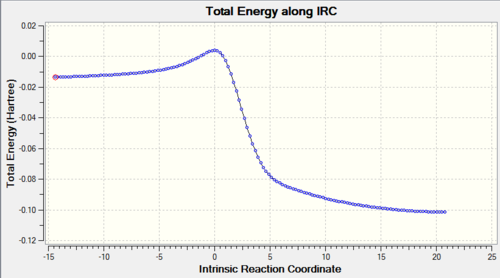
Using IRC calculations, the total energy along the IRC can be measured, as well as visualising the reaction coordinate. This becomes helpful when we try to examine and analyse the transition states, as well as understanding the reaction trajectory. The calculations can be found in Table. 3 below.
Table 3: IRC Calculations and Total Energy along IRC for Different Pathways Pathway IRC Total Energy along IRC Endothermic Diels-Alder Reaction 
Exothermic Diels-Alder Reaction 
Cheletropic Reaction 
Activation and Reaction Energies
Not only the IRC of the reaction was calculated, further investigation was done to examine the relative energies of the reactants, transition states and products. The data collected are represented below in Table.4. Same with exercise 2, the reactants were the sum of individual energy of O-xylylene and SO2. Assumptions were again made such that we assume the two reactants were placed at an infinite distance apart so that there will not be any interaction between the two molecules. A reaction coordinate diagram, Figure 9 was also produced to accompany the data collected from Table.4.
|
 | |||||||||||||||||||||||||||||||||
(Your reactants energy is too high and if you had included the log files I would have been able to see why Tam10 (talk) 10:35, 7 March 2018 (UTC))
Each of the reaction is colour-coded and their activation energy and reaction energy are shown in the diagram. As depicted in Figure.9, we can see that despite having the highest activation energy, the cheletropic reaction forms that most stable product and it is thermodynamically favoured. This can be due to the fact that the two strong S=O bonds are retained, as well as the formation of the aromatic ring on the other side. Conversely, the Diels-Alder reactions have lower activation energies. Amongst which, the endothermic transition state has a lower activation energy than the exothermic transition state. This can be explained using the same principle as described above, in which secondary orbital interaction has played a role in stabilising the transition state of the endothermic product, giving it the kinetic product amongst those three reactions. The reaction energy for both the exothermic and endothermic reaction is quite similar, with the exothermic product being slightly more stable. This might be due to the steric clash experience between the oxygen on S=O and the H atoms on the 6-membered ring.
Discussion: Possible Side Reaction between o-xylylene &SO2 - Internal Diels-Alder Reaction
By closely examining our reactants, we can also observe that there are two cis-butadiene presents in the molecule. The above discussion mainly dealt with the reaction between the terminal diene and SO2. Here, we discuss the possibility of an internal Diels-Alder Reaction, where the cis-butadiene in the close 6-membered ring reacts with SO2. The reaction scheme of this reaction is found below in Figure.10. These reactions are stimulated using Gaussian and the structures for the transition states and products are optimised using the semi-empirical PM6 method.
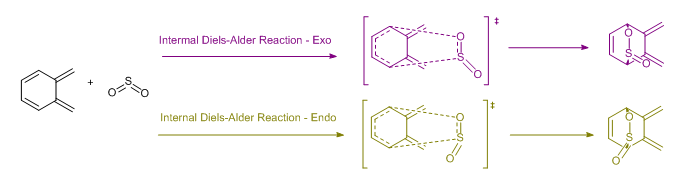
Same with the reactions above, the activation energies and reaction energies of the two internal Diels-Alder product: Endothermic and Exothermic, are calculated and tabulated in the Table.5 below. The reaction coordinate of this reaction is also drawn alongside with the original Diels-Alder reaction for ease of comparison. The reaction coordinate of this internal Diels-Alder reaction is presented in Figure.11 below.
|
 | |||||||||||||||||||||||||||
As we can see from the calculations for both the activation energy and reaction energy, both the internal Diels-Alder reaction are kinetically unfavourable as well as thermodynamically unfavourable. The internal Diels-Alder reactions have higher activation energy as compared to the original Diels-Alder reaction. Following the same reason as above, the endothermic reaction has a lower activation energy than exothermic reaction due to the secondary orbital stabilisation of the endothermic transition state. This internal Diels Alder reaction is unfavourable since there is a larger change in structure as compared to the original terminal Diels-Alder Reaction. The cyclohexadiene ring has to change from its planar geometry to a chair/ boat confirmation, which is indicated by the change from largely sp2 hybridised C-C bond in reactants to sp3 hybridised C-C bond in the product.
IRC calculations were also conducted and can be found below on Table.7
| Pathway | IRC | Total Energy along IRC |
|---|---|---|
| Endothermic Diels-Alder Reaction |  |
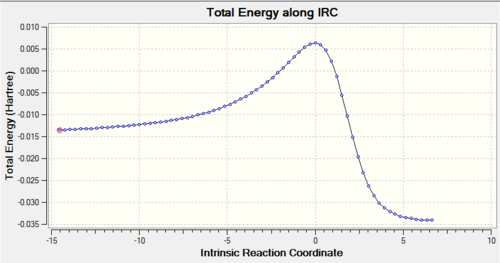 |
| Exothermic Diels-Alder Reaction |  |
 |
Discussion : Possible Side Reaction of o-xylylene - Electrocyclic Reaction
Other possible side reaction also includes an electrocyclic reaction of the xylylene itself, which forms benzocyclobutane. The reaction scheme is found in Figure.12 below.

If such reaction was to occur, it would result in the formation of an aromatic ring, which is thermodynamically favourable, and also the formation of a 4 membered ring. The electrocyclic reaction would undergo a conrotation reaction, as suggested by the HOMO of xylylene as depicted below in Figure.13. In order for the two terminal alkenes to interact and form a sigma bond, a conrotation reaction must happen.
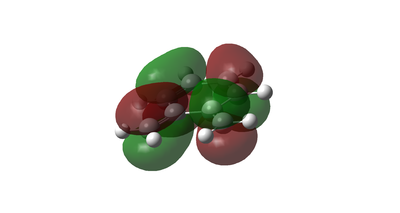
However, such formation is not observed when we optimise xylylene. The optimised structure remains as xylylene instead of forming benzocyclobutane. This means that even though the structure is thermodynamically stabilised, it is not kinetically favoured. This must imply that energy gained from the formation of the aromatic ring is not enough to overcome the activation barrier it has for such electrocyclic reaction to occur. One possible explanation is that the formation of the 4-membered cyclobutane is energetically more costly than the energy released from bond formation. Ring strain is present in the 4 membered ring, which the 90o bond angle has caused energy penalty for sp3 hybridised carbon which prefers 109.5o. This electrocyclic reaction obeys the Woodward Hoffmann where there are 4n π electrons and n=1. This suggests that the reaction is conrotatory and also thermally allowed.
(No this isn't true. Optimisations will bring you to a local minimum. benzocyclobutane is in another part of the PES. If you start near benzocyclobutane then you can minimise to it. What you are thinking about is a barrierless reaction which is an intrinsic instability. The TS that links them is fairly straightforward to find using the methods we've provided Tam10 (talk) 10:35, 7 March 2018 (UTC))
Conclusion
All in all, the exercises that we have conducted have helped us to explore Diels-Alder reaction between different substrates. Three kinds of Diels-Alder reaction were stimulated and analysed using Gaussview: standard Diels-Alder reaction, Inverse electron demand Diels-Alder reaction, and heteroatom-substituted Diels-Alder reaction. All three reactions are either optimised using the semi-empirical PM6 method or Density Functional Theory method to B3LYP/6-31G(d) level.
In Exercise 1, we have conducted the standard Diels-Alder reaction, which we analysed the molecular orbitals of the transition state and reactants. We have also conducted a bond length analysis to find that our calculated values agree closely with the literature values. A vibrational analysis was done and confirmed that the transition state of our reaction was correctly located, as it contains only one imaginary frequency.
In Exercise 2, we have conducted an inverse electron demand Diels-Alder reaction. As the dienophile is no longer ethylene, we can stimulate the reaction to probe the formation of both endothermic and exothermic products. Molecular orbital diagram for both of the endothermic and exothermic transition states was drawn and compared. It is found, by running single point energy calculation, that the HOMO-LUMO gap for endothermic transition state is bigger than that of the exothermic transition state. Activation energy and reaction energy was also calculated for the reactions and was found that the endothermic pathway is both the kinetic and thermodynamic product. This can be explained by the secondary orbital interaction effect that stabilises the endothermic transition state, as well as the steric clash that the exothermic product which destabilises the product.
In Exercise 3, a heteroatom-substituted Diels-Alder reaction is conducted. In this case, not only the Diels-Alder reaction is present, the cheletropic reaction between the SO2 fragment and xylylene can also be calculated. IRC calculations have helped us to visualise the reaction progress between the different reactions and aid us to understand the reaction trajectory. Activation energy and reaction energy was also tabulated for these reactions and being compared to each other. The cheletropic pathway is found to be the thermodynamically preferred pathway, while the endothermic Diels-Alder reaction pathway has yield the kinetic product. Other possible reacts, such as the internal Diels-Alder reaction and the electrocyclic reaction are also calculated and compared against the normal reactions. These reactions are found to have higher activation energy or are thermodynamically not favourable hence they are not competing process of the reaction.